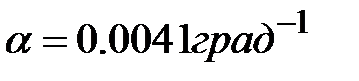| Латунь | Алюминий | Сталь | |
| Масса, гр | 158 | 50 | 140 |
| Габаритные размеры мм´мм | 30´35,5 | 30´35,5 | 30´35,5 |
4. Записать начальную температуру пустого калориметра.
5. Включить тумблер «ВКЛ» в модуле «НАГРЕВ». Регулятором модуля установить заданную мощность нагрева. Записать значения напряжения и тока.
6. Записать время нагрева пусто калориметра на 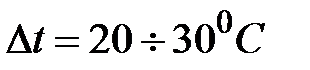 .
.
7. Отключить нагрев. Для быстрого охлаждения калориметра открыть крышку, опустить в калориметр один из образцов. Температура начнет понижаться.
8. Установить исследуемый образец в калориметр, подождать, когда установиться постоянная температура. Записать начальную температуру калориметра с образцом.
9. Нагрев должен осуществляться при тех же значениях напряжения и тока, что и для пустого калориметра.
10. Записать время нагрева калориметра с исследуемым образцом на 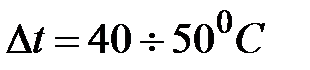 (значение
(значение 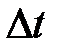 выбрано в пункте 6).
выбрано в пункте 6).
11. Отключить нагрев. Вынуть образец. Для вынимания образца надо повернуть по часовой стрелке винт в нижней части калориметра, после чего вынуть его рукояткой.
12. Заполнить таблицу 2-7.3
Таблица 2-7.3.
| № п.п. | Измеряемая величина | Пустой калориметр | Исследуемые образцы | ||
| латунь | алюминий | сталь | |||
| 1 |
| ||||
| 2 | m, кг | ||||
| 3 | 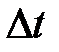 , 0С , 0С
| ||||
| 4 | t, сек | ||||
| 5 | 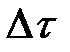 , сек , сек
| ||||
| 6 | С, 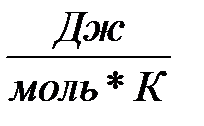
| ||||
Контрольные вопросы и задания
1. Что называется теплоемкостью тела?
2. В чем заключается суть классической теории теплоемкости твердых тел? Сформулируйте закон Дюлонга и Пти.
3. Каковы недостатки классической теории теплоемкости? Когда они проявляются?
4. Из каких положений исходит квантовая теория Эйнштейна?
5. Проанализируйте формулу теплоемкости Эйнштейна (9) при Т®¥ и Т®0.
6. Какие усовершенствования внесены в теорию теплоемкости твердых тел Дебая? Для какого интервала температур справедлив закон кубов Дебая?
7. Каково физическое содержание понятия характеристической температуры Дебая?
8. Почему при комнатной температуре теплоемкость алмаза не подчиняется закону Дюлонга и Пти?
Список рекомендуемой литературы
1. Кикоин А.К. Кикоин И.К. Молекулярная физика. М. : Наука, 1976.
2. Матвеев А. Н. Молекулярная физика. М. : Высш. шк., 1987.
3. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М. : Наука, 1993, Т. 2.
Лабораторная работа 2-8
Теплопроводность газов
Цель работы: изучить процессы переноса в воздухе, рассмотреть теоретические аспекты явления теплопроводности.
Задача работы: освоить методику измерений коэффициента теплопроводности методом цилиндрического слоя.
Теория
Беспорядочные движения частиц газа обусловливают процессы диффузии, теплопроводности, внутреннего трения и т. д. Все эти явления имеют много общего и объединяются общим названием явления переноса. В настоящей работе изучается явление теплопроводности в воздухе.
| Рис. 2-8. 1 |
| Q |
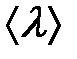
|
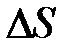
|
| Z |

Известно три способа передачи тепла: конвекция, теплопроводность, излучение. В первых двух случаях в процессе передачи тепла участвует вещество. Процесс конвекции обусловлен разностью удельных весов нагретых и холодных слоев газа. Теплопроводность - процесс переноса тепла, отличительной чертой которого является атомно-молекулярный характер передачи энергии. Сталкиваясь, молекулы передают друг другу “эстафетным способом” кинетическую энергию. Процесс теплопроводности наблюдается в системе при наличии градиента температуры.
Предположим, что в некотором объеме газа (рис. 2-8.1), в положительном направлении оси Z существует градиент температуры  . Тогда в противоположном направлении, в области более низких температур, будет наблюдаться поток тепла, который по закону Фурье пропорционален градиенту температуры:
. Тогда в противоположном направлении, в области более низких температур, будет наблюдаться поток тепла, который по закону Фурье пропорционален градиенту температуры:
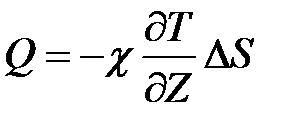 , ,
| (2-8.1) |
где 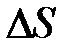 - величина площадки, через которую определяется поток тепла, c - коэффициент теплопроводности газов. Знак “минус” подчеркивает, что поток энергии и вектор градиента температуры направлены в противоположные стороны. Величина коэффициента теплопроводности согласно молекулярно-кинетической теории определяется как
- величина площадки, через которую определяется поток тепла, c - коэффициент теплопроводности газов. Знак “минус” подчеркивает, что поток энергии и вектор градиента температуры направлены в противоположные стороны. Величина коэффициента теплопроводности согласно молекулярно-кинетической теории определяется как
 , ,
| (2-8.2) |
где 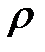 - плотность газа,
- плотность газа, 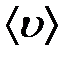 - средняя скорость теплового движения, λ - средняя длина свободного пробега,
- средняя скорость теплового движения, λ - средняя длина свободного пробега, 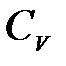 - удельная теплоемкость газа при постоянном объеме. Если в уравнении (2-8.1) градиент температуры -
- удельная теплоемкость газа при постоянном объеме. Если в уравнении (2-8.1) градиент температуры -  принять равным 1, то размерность коэффициента теплопроводности будет [вт/мК]. Из выражения (2-8.2) следует, что c не зависит от давления, так как плотность газа пропорциональна, а длина свободного пробега обратно-пропорциональна давлению газа
принять равным 1, то размерность коэффициента теплопроводности будет [вт/мК]. Из выражения (2-8.2) следует, что c не зависит от давления, так как плотность газа пропорциональна, а длина свободного пробега обратно-пропорциональна давлению газа 
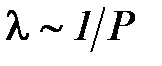 [1]. Независимость коэффициента теплопроводности от давления осуществляется не всегда. Так, для давлений, при которых длина свободного пробега молекул становится соизмерима с размерами сосуда, содержащего газ, или больше этой величины, т. е.
[1]. Независимость коэффициента теплопроводности от давления осуществляется не всегда. Так, для давлений, при которых длина свободного пробега молекул становится соизмерима с размерами сосуда, содержащего газ, или больше этой величины, т. е. 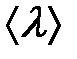 ≥ l , эта зависимость нарушается. В этом случае столкновения между молекулами самого газа перестают играть главную роль, существенными становятся только столкновения молекул со стенками сосуда, в котором заключен газ. Молекула, столкнувшись с горячей стенкой, получает от нее кинетическую энергию и переносит ее к более холодной стенке, не испытывая промежуточных столкновений. Ясно, что в таком случае перенос тепла будет происходить тем медленнее, чем меньше носителей тепла, т. е., чем больше разряжен газ. Такой перенос формально может быть описан прежней формулой 4, но величину λ следует заменить величиной l - расстоянием между стенками сосуда [2]. Процесс передачи тепла в этом случае носит название «теплопередача».
≥ l , эта зависимость нарушается. В этом случае столкновения между молекулами самого газа перестают играть главную роль, существенными становятся только столкновения молекул со стенками сосуда, в котором заключен газ. Молекула, столкнувшись с горячей стенкой, получает от нее кинетическую энергию и переносит ее к более холодной стенке, не испытывая промежуточных столкновений. Ясно, что в таком случае перенос тепла будет происходить тем медленнее, чем меньше носителей тепла, т. е., чем больше разряжен газ. Такой перенос формально может быть описан прежней формулой 4, но величину λ следует заменить величиной l - расстоянием между стенками сосуда [2]. Процесс передачи тепла в этом случае носит название «теплопередача».
Для воздуха при 200С длина свободного пробега молекул выражается эмпирической формулой [3]:
λ = 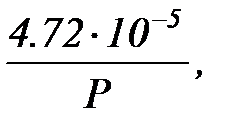
где Р- давление газа. Пользуясь этим соотношением, можно оценить то давление, при котором длина свободного пробега становится сравнима с размерами эмпирического объема.
Таким образом, независимость коэффициента теплопроводности от плотности газа имеет место лишь до тех пор, пока длина свободного пробега мала по сравнению с размерами сосуда. Когда λ и l становятся соизмеримы друг с другом, при уменьшении плотности газа коэффициент c начинает убывать. Это убывание идет по линейному закону: коэффициент c становится пропорционален плотности газа, при низком давлении теплопроводность очень мала. На этом принципе основано устройство сосудов Дюара, в которых теплоизоляция между стенками сосудов достигается с помощью вакуума.
В то же время величина c при любом давлении зависит от температуры, так как средняя скорость молекул, входящая в уравнение (2-8.2), зависит от температуры 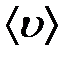
 .
.
Постановка задачи
Для изучения явления теплопроводности рассмотрим систему, состоящую из двух цилиндров с радиусами r1 и r2 (рис. 2-8.2,а). Температуры цилиндров соответственно равны Т1 и Т2 и поддерживаются с помощью внешнего источника тепла постоянными. Внутренний цилиндр может быть, в частности, просто проволокой, по которой пропускается электрический ток, и она служит нагревателем, т.е. Т1>Т2 (рис. 2-8.2,б). Поток тепла направлен от более нагретой внутренней поверхности к внешней. В случае стационарного потока распределение температур между цилиндрами будет постоянно во времени.
Используя соотношение (2-8.1), получим, что поток тепла Q в единицу времени через цилиндрическую поверхность высотой 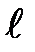 и радиусом r выражается формулой
и радиусом r выражается формулой
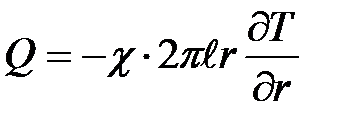 . (2-8.1)
. (2-8.1)
Интегрируя это выражение при значениях температур внутреннего и внешнего цилиндров Т1 и Т2 , получим
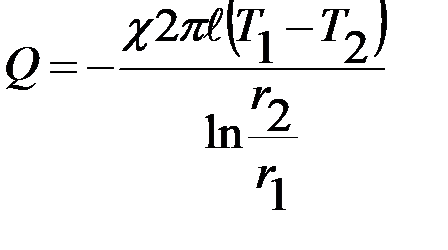 . (2-8.2)
. (2-8.2)
| r2 |
| r1 |
| r |
| а |
| r1 |
| r |
| r2 |
| б |
| Рис. 2-8.2. Система из двух цилиндров |
В стационарном состоянии поток тепла Q можно принять равным мощности нагревателя W , и тогда коэффициент теплопроводности имеет вид
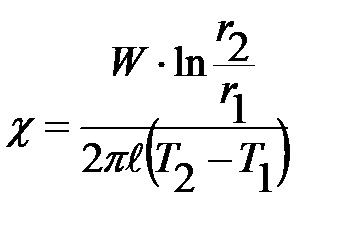
| (2-8.3) |
На практике все температуры мы определяем по шкале Цельсия, которая с абсолютной температурой связана соотношением t = ( T -273)0C. Следовательно, разность температур Т1 -Т2 в выражении (2-8.3) может быть подставлена в (2-8.3) в градусах Цельсия t 1 - t 2 (как она и определяется в эксперименте).
Таким образом, для определения величины коэффициента теплопроводности надо определить: количество тепла, переносимого от внутренней поверхности к внешней, разность температур между внутренним и внешним цилиндром, размеры системы. Все эти величины находятся из эксперимента.
Следует иметь в виду, что полученные значения будут несколько завышены, так как в процессе теплопроводности определенную роль могут играть процессы излучения и конвекции. Влияние конвекции на полученные экспериментальные результаты можно оценить, определяя коэффициент теплопроводности при разных давлениях воздуха. Известно, что с увеличением давления интенсивность конвекционного переноса тепла растет. Если в результате эксперимента обнаружится тенденция роста коэффициента теплопроводности с увеличением давления, то ее можно объяснить наличием конвективных потоков. Роль теплового излучения может быть оценена с помощью закона Стефана – Больцмана, по которому с единицы поверхности абсолютно черного тела излучается энергия W = 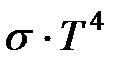 , где Т – абсолютная температура тела, а
, где Т – абсолютная температура тела, а  . Полная энергия, передаваемая при излучении от одного цилиндра к другому, не превышает
. Полная энергия, передаваемая при излучении от одного цилиндра к другому, не превышает
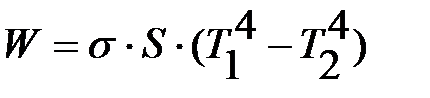 , ,
| (2-8.4) |
где S – площадь поверхности внутреннего цилиндра.
Описание установки
Для измерения коэффициента теплопроводности воздуха в данной работе используется лабораторная установка ФПТ 1-3. Установка представляет собой конструкцию настольного типа, состоящую из основных частей: 1) приборный блок, 2) рабочий элемент.
Приборный блок представляет собой единый конструктив со съемной крышкой, съемными лицевыми панелями. Внутри блока размещена печатная плата с радиоэлементами, органы подключения, регулирования, трансформаторы.
Лицевая панель блока условно разделена на три функциональных узла:
1. «НАПРЯЖЕНИЕ» осуществляет управление работой цифрового контролера для измерения напряжения.
2. «НАГРЕВ» осуществляет включение и регулирование нагрева нити.
3. «СЕТЬ» осуществляет подключение установки к сети питающего напряжения.
Рабочий элемент представляет собой коробчатый конструктив, укрепленный на стойке. Несущими узлами этого блока являются панель и кронштейн, скрепленные между собой винтами.
Между выступающими частями панели в текстолитовых фланцах зажата стеклянная трубка. По оси трубки натянута вольфрамовая нить. Между панелью и кронштейном размещен вентилятор для охлаждения трубки. На панели установлены цифровой контроллер для измерения температуры и цифровой контроллер для измерения напряжения.
В лабораторной установке тепловой поток создается путем нагрева нити постоянным током и определяется по формуле
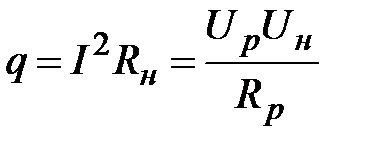 , (2-8.5)
, (2-8.5)
где 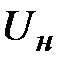 - падение напряжения на нити;
- падение напряжения на нити;
 - падение напряжения на эталонном резисторе;
- падение напряжения на эталонном резисторе;
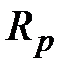 - сопротивление эталонного резистора (
- сопротивление эталонного резистора ( 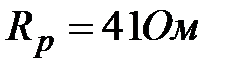 ).
).
Разность температур нити и трубки: 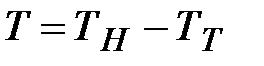 , где
, где 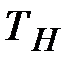 – температура нити,
– температура нити, 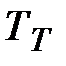 - температура трубки, равна температуре окружающего воздуха.
- температура трубки, равна температуре окружающего воздуха.
Температура трубки в процессе эксперимента принимается постоянной, т. к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
Температура нити тем выше, чем больше протекающий по ней ток. С помощью температуры меняется сопротивление нити, измеряемое методом сравнения падения напряжений на нити и на эталонном резисторе.
Разность температур нити и трубки определяется по формуле
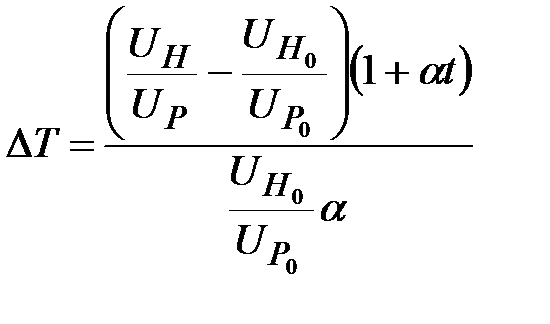 , (2-8.6)
, (2-8.6)
где 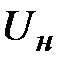 - падение напряжения на нити в нагретом состоянии;
- падение напряжения на нити в нагретом состоянии;
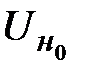 - падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10мА);
- падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10мА);
 - падение напряжения на эталонном резисторе при нагреве нити;
- падение напряжения на эталонном резисторе при нагреве нити;
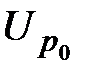 - падение напряжения на эталонном резисторе при температуре окружающего воздуха;
- падение напряжения на эталонном резисторе при температуре окружающего воздуха;
 - температурный коэффициент сопротивления
- температурный коэффициент сопротивления 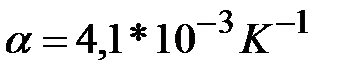 ;
;
t – температура воздуха.
Порядок выполнения работы
1. Вывести на минимум ручку потенциометра в модуле «НАГРЕВ».
2. Подать на установку питание, включив тумблер «ВКЛ» в модуле «СЕТЬ».
3. Включить тумблер «ВКЛ» в модуле «НАГРЕВ».
4. Нажать кнопку  (режим измерения падения напряжения на эталонном резисторе).
(режим измерения падения напряжения на эталонном резисторе).
5. Установить регулятором «НАГРЕВ» напряжение  не более 0,06В (негреющий ток).
не более 0,06В (негреющий ток).
6. Нажать кнопку 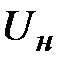 (режим измерения падения напряжения на нити) и зарегистрировать показания цифрового индикатора.
(режим измерения падения напряжения на нити) и зарегистрировать показания цифрового индикатора.
7. Рассчитать тепловой поток по формуле (2-8.5).
8. Нажать кнопку  и установить рукояткой «НАГРЕВ» напряжение в диапазоне 0,3-6,5В. Заполнить табл. 2-8.1 измерений.
и установить рукояткой «НАГРЕВ» напряжение в диапазоне 0,3-6,5В. Заполнить табл. 2-8.1 измерений.
таблица 2-8.1
 B B
|  B B
| 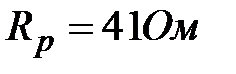
|
| |
 0C 0C
| 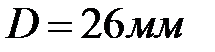
| 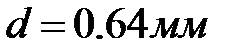
|
| |
| № п.п. |  , В , В
| 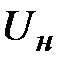 , В , В
|  , 0С , 0С
| 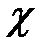
|
| 1 | 2,8 | |||
| 2 | 3,8 | |||
| 3 | 4,8 | |||
| 4 | 5,8 | |||
9. Выждать некоторое время для стабилизации теплового режима и определить падение напряжения на нити 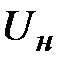 .
.
10. После измерения вывести рукоятку «НАГРЕВ» в крайнее левое положение.
11. Рассчитать разность температур по формуле (2-8.6) и определить коэффициент теплопроводности по формуле (2-8.3).
12. Рассчитать зависимость температуры проволоки от мощности нагрева W, построить ее график. Результаты занести в табл2-8.2:
таблица 2-8.2
| № п.п. |  , В , В
| 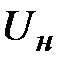 , В , В
| 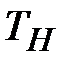 , 0С , 0С
| 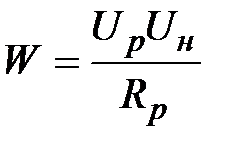
|
| 1 | 2,8 | |||
| 2 | 3,8 | |||
| 3 | 4,8 | |||
| 4 | 5,8 |
13. Оценить величину мощности излучения проволоки по закону Стефана–Больцмана.
Контрольные вопросы и задания
1. Назовите три механизма передачи тепла. В чем их физическая суть?
2. Каковы выражение и размерность коэффициента теплопроводности?
3. Как выводится размерность коэффициента теплопроводности?
4. Каков физический смысл коэффициента теплопроводности?
5. Как зависит c от давления газа и от градиента температуры газа?
6. На каком принципе устроен сосуд Дьюара?
Список литературы
1. Матвеев А. Н. Молекулярная физика М. : Высш. шк., 1987.
2. Сивухин Л. В. Общий курс физики : Термодинамика и молекулярная физика М. : Наука, 1990.
3. Булкин П.С. Общий физический практикум, Молекулярная физика М. : МГУ, 1988.
4. Бекнев В.С., Епифанов В.М., Леонтьев А.И. и др. Газовая динамика. Механика жидкости и газа / Под общ.ред. А.И. Леонтьева М.: Изд-во МГТУ им. Н.Э. Баумана, 1997.
5. Луканин В.Н., Шатров М.Г., Камфер Г.М. и др. Теплотехника / Под ред. Луканина В.Н. М. : Высш. шк., 1999.
6. Общие требования к оформлению текстовых и графических работ студентов. СТО ИрГТУ. 005-2007
Приложение 1
Дата: 2019-03-05, просмотров: 388.
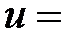 В
В 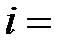 А
А