Задача работы: методом охлаждения получить графики зависимости теплоемкости алюминиевого и стального образцов от температуры.

Теория

Теплоемкостью тела С называется отношение бесконечно малого изменения внутренней энергии этого тела dU к изменению его температуры dT:

С = .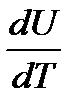

(2-7.1)

Внутренняя энергия совпадает с энергией покоя тела (системы) и включает в себя энергию всех внутренних движений в теле и энергию взаимодействия всех частиц, составляющих это тело, включая молекулы, атомы и ионы, электроны, а также нуклоны в ядрах. Заметим сразу, что потенциальные энергии электронных оболочек атомов и ионов, потенциальные и кинетические энергии нуклонов не играют существенной роли при обычных не очень высоких температурах, когда не идут процессы ионизации и возбуждения соответствующих частиц.

Различают удельную теплоемкость – теплоемкость единицы массы вещества (одного килограмма, грамма), молярную теплоемкость – теплоемкость одного моля вещества. Единицы измерения удельной теплоемкости – Дж/кг·К (внесистемная – кал/кг·К), молярной теплоемкости – Дж/моль·К (кал/моль·К).

Различают теплоемкость при постоянном давлении С_р и теплоемкость при постоянном объеме С _v. Для таких систем, как твердое тело и жидкость (в отличие от газа), изменение объема при нагревании относительно невелико и разность С_р–С_v для одноатомных твердых веществ при 100 ^оС составляет десятые, сотые и даже тысячные доли газовой постоянной R. Поэтому зависимостью теплоемкости от изменения объема при нагревании твердого тела обычно пренебрегают и говорят просто об удельной теплоемкости твердого тела С _v, связывая ее с изменением внутренней энергии единицы массы твердого тела при нагревании на один градус.

Классическая теория теплоемкости твердых тел (кристаллов)

Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы, принимаемые за материальные точки. Атомы совершают тепловые колебания около положений равновесия. Если колебания малы, то их можно считать гармоническими. Энергия каждого атома слагается из кинетической и потенциальной. На каждую степень свободы приходится в среднем кинетическая энергия ½ k Т. Из механики известно, что при гармонических колебаниях средние значения кинетической и потенциальной энергии одинаковы. Таким образом, среднее значение полной энергии, приходящейся на одну колебательную степень свободы, равно:

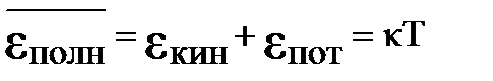.                      (2-7.2)

    Рассчитаем теплоемкость кристаллической решетки на основе классических представлений. Для простоты будем считать, что все атомы одинаковы. Каждый атом обладает тремя колебательными степенями свободы, а потому на него приходится средняя энергия 3кТ. Умножив эту величину на число Авогадро N_a, найдем внутреннюю энергию твердого тела:

U = 3 N_a 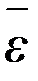 = N_a 3 kT = 3 RT ,                    (2-7.3)

здесь учтено, что N_a · k = R. Отсюда для молярной теплоемкости твердого тела получаем:

C_v = 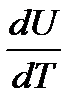 =3R ≈ 24,9 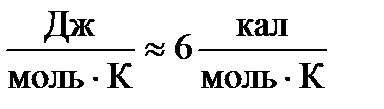.                      (2-7.4)

Этот результат находится в согласии с экспериментально установленным в 1819 г. законом (правилом) П.Дюлонга и А.Пти: молярная теплоемкость всех химически простых кристаллических твердых тел постоянна и равна 3 R (R – универсальная газовая постоянная). Мы видим, что закон Дюлонга и Пти находит простое объяснение в классической теории теплоемкости. Он сравнительно хорошо подтверждается на опыте для многих веществ при не слишком низких температурах.

    Рассмотрим твердое тело, которое является химическим соединением, например, NaCl. Его кристаллическая решетка построена из атомов различных типов. Очевидно, молекулярная масса химического соединения равна сумме атомных масс всех атомов, из которых состоит молекула этого соединения. Согласно предыдущим рассуждениям, если в молекуле n атомов, то на молекулу приходится в среднем энергия 3nkT. Молярная теплоемкость будет 3nkN_a = 3nR, т.е. она в n раз больше, чем у того же вещества, если бы его молекулы были одноатомными. Иными словами, молярная теплоемкость твердого соединения равна сумме молярных теплоемкостей элементарных веществ, из которых оно состоит. Это правило было найдено эмпирически и называется законом Джоуля и Коппа. Джоуль высказал его 1844 г. Но только в 1864 г. закон был окончательно сформулирован и подтвержден множеством фактов, полученных Коппом. Следует заметить, что закон Джоуля и Коппа в приведенной выше формулировке обладает большей общностью, чем закон Дюлонга и Пти. Закон Дюлонга и Пти может нарушаться, т. е. атомные теплоемкости химических элементов, входящих в соединение, могут отличаться друг от друга, но закон Джоуля и Коппа остается при этом справедливым.