Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Обоснование метода

На твердый шарик, падающий в жидкости, действуют три силы: сила тяжести, сила Архимеда и сила трения шарика о жидкость. Эти силы равны соответственно .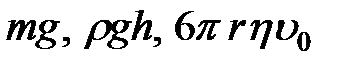

Обозначим скорость шарика относительно жидкости через 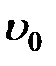. Молекулы жидкости в слое, прилегающем к шарику, движутся со скоростью . Распределение жидкостей в соседних слоях, увлекаемых силами внутреннего трения, должно иметь вид, изображенный на рис. 2-4.5. В непосредственной близости от поверхности шара эта скорость равна 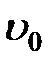, а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии L от поверхности шарика. Очевидно, что чем больше радиус шара, тем большая масса жидкости вовлекается в движение, и L должно быть пропорционально :

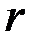L = kr .                            (2-4.16)

Величина коэффициента пропорциональности несколь­ко различна для пе­редней и задней частей тела, поэтому под градиентом скорости следует понимать среднее значение градиента скорости на поверхности шара

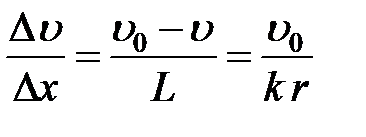  .                  (2-4.17)

Полная сила трения, испытываемая движущимся шариком,

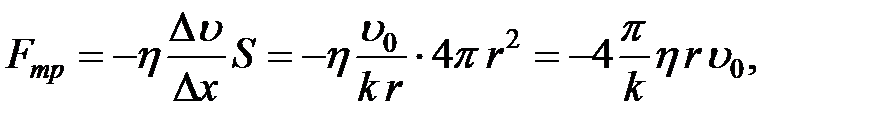             (2-4.18)

где .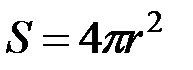

Согласно Стоксу, величина 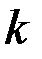 для шара равна 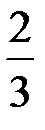. Следовательно,

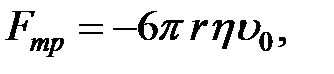                       (2-4.19)

т. е. сила трения прямо пропорциональна вязкости жидкости, радиусу шара и скорости его движения. Выражение (2-4.19) носит название закона Стокса:

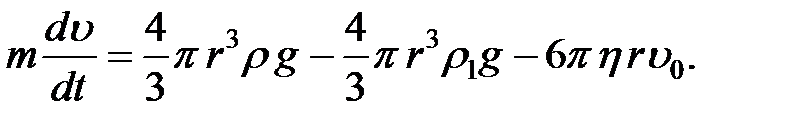         (2-4.20)

Рис. 2-4.5. Поле сил

Рис. 2-4.5. Поле сил

В случае падения шарика в жидкости, все три силы будут направлены по вертикали. Если шарик движется равномерно, то такое движение шарика называется установившимся. Физически это означает, что сила трения и сила Архимеда уравновешиваются силой тяжести, т. е. движение происходит по инерции с постоянной скоростью. Тогда уравнение (18) можно переписать:

(2-4.21)

Последнее выражение позволяет определить коэффициент внутреннего трения в жидкости, в которой движется шарик. Так как жидкость всегда находится в каком-то сосуде, имеющем стенки, то учет наличия стенок несколько изменит выражение для коэффициента вязкости. Для жидкости, находящейся в цилиндре с радиусом 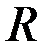, коэффициент вязкости равен

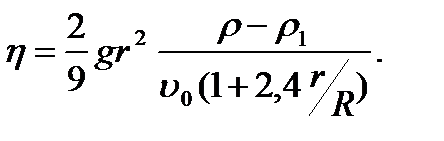                                 (2-4.22)

Экспериментальная часть

Приборы и принадлежности

Стеклянный цилиндр с исследуемой жидкостью плотностью , микрометр, штангенциркуль, секундомер, шарики из материала, плотность которого .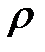

Описание прибора

Прибор состоит из стеклянного цилиндра, наполненного исследуемой жидкостью и имеющего две горизонтальные метки, расположенные на расстоянии 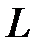 друг от друга. Верхняя метка должна быть ниже уровня жидкости на 5-8 см (рис. 2-4.

Рис. 2-4.6. Стеклянный цилиндр

6).

Порядок выполнения работы

Для определения коэффициента внутреннего трения используются шарики, диаметр которых определяется микрометром.

Желательно расположить прибор так, чтобы глаз наблюдателя находился на уровне верхней метки. При опускании шарика в жидкость необходимо учесть, что: 1) траектория его движения должна проходить как можно ближе к оси цилиндра, 2) движение шарика в жидкости должно начинаться с нулевой начальной скоростью. Прежде чем включать секундомер, необходимо выждать установления равномерной скорости движения шарика. В момент прохождения шарика мимо верхней метки включают секундомер; в момент прохождения шарика через нижнюю метку – выключают. Считая движение шарика между метками равномерным, получают скорость его движения 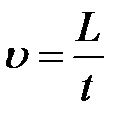. Внутренний радиус цилиндрического сосуда  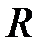определяют штангенциркулем, опыт с разными шариками повторяют 10 раз.

Измерение диаметра шариков нужно производить непосредственно перед опусканием каждого из них в жидкость, во избежание несоответствия в результатах скорости шариков их диаметрам.

Примечание. Во время опыта цилиндр с исследуемой жидкостью должен быть хорошо освещен, но лампу не следует ставить близко к сосуду во избежание нагрева исследуемой жидкости.

Результаты экспериментальных измерений и расчетов по формуле (2-4.22) занести в табл. 2-4.2:

Таблица 2-4.2

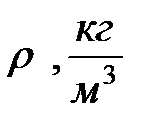
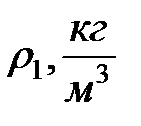
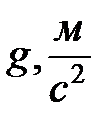
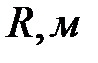
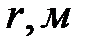
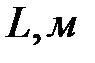
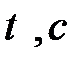
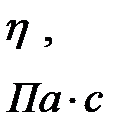
Оценить погрешность эксперимента.

Контрольные вопросы и задания

1. В чем заключается явление внутреннего трения в жидкости?

2. Что понимается под коэффициентами кинематической и динамической вязкости жидкостей?

3. Как изменяется коэффициент вязкости от температуры?

4. Какое движение жидкости называется ламинарным?

5. Какие силы действуют на шарик, движущийся в жидкости?

6. Какая кривая называется реологической, каков ее смысл?

7. Какие жидкости называются ньютоновскими?

8. Преобразовав путем разделения переменных и интегрированием формулу 3, проанализировать зависимость скорости слоев жидкости от координаты z.

Список рекомендуемой литературы

1. Кикоин А.К., Кикоин И.К. Молекулярная физика. М. : Наука, 1976.

2. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика. М. : Наука, 1990.

3. Матвеев А.Н. Молекулярная физика. М. : Высш. шк., 1987.

4. Гинзбург В.Л., Левин Л.М., Сивухин Д.В., Яковлев И.А.. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика / Под редакцией Д.В. Сивухина. М. : Наука, 1988.

5. Булкин П.С., Попова И.И. Общий физический практикум. Молекулярная физика / Под редакцией А.Н. Матвеева и Д.Ф. Киселева. М. : Изд-во Моск. Ун-т., 1988.

6. Савельев И.В. Курс общей физики. М. : Наука, 1986. Т.1.

7. Трофимова Т.И. Курс физики. М. : Высш. шк., 2001.

Лабораторная работа  2-5