Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В теории Дебая (1912 г.), далее развитой Борном, кристалл рассматривается как сплошное (непрерывное) упругое тело (атомы которого очень сильно связаны между собой), участвующее в колебаниях со всевозможными частотами. Тепловые колебания отождествляются с упругими стоячими волнам в теле. Простейшей аналогией таких колебаний являются колебания натянутой струны. Число возможных колебательных состояний принимается равным числу степеней свободы 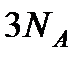, причем берутся наиболее медленные, т.е. основные колебания. Частоты этих, так называемых нормальных колебаний, весьма различны, начиная от низких, в сотни герц, и кончая инфракрасными, порядка 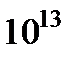Гц. Суперпозиция этих колебаний с различными случайными амплитудами и фазами дает тепловое движение твердого тела. Величина энергии этого движения .

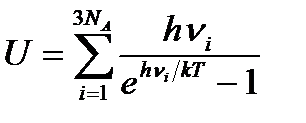Вычисление нормальных частот 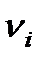 является весьма трудной задачей. Результаты вычисления хорошо совпадают с опытом.

Из теории Дебая следует, что при очень низких температурах теплоемкость одноатомного твердого тела пропорциональна третьей степени абсолютной температуры:

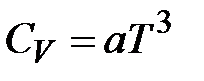                                 (2-7.10)

Это закон кубов Дебая, который хорошо объясняет ход теплоемкости вблизи абсолютного нуля. Внутренняя энергия твердого тела вблизи абсолютного нуля пропорциональна четвертой степени абсолютной температуры ( 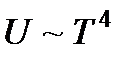). При высоких температурах теория Дебая привела к результатам, совпадающим с классическими результатами (закон Дюлонга и Пти) (рис. 2-7.2).

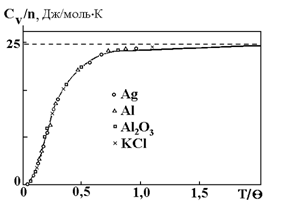
Рис. 2-7.2. Температурные зависимости теплоемкости различных веществ

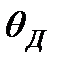Весьма важную роль в теории Дебая играет понятие характеристической температуры Дебая , начиная с которой теплоемкость быстро убывает с понижением температуры. Это та температура, при которой энергия тепловых движений  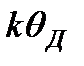становится равной максимальной энергии осцилляторов: 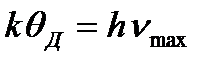, отсюда .

 

 

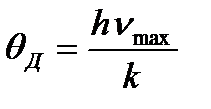При температурах, значительно меньших 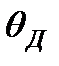, теплоемкость убывает пропорционально кубу температуры (”закон 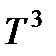”), что соответствует опытным данным. Температура Дебая  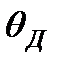может считаться границей между высокими и низкими температурами. При температурах выше  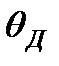теплоемкость следует классическому закону (см. рис. 2-7.2), ниже этой температуры для объяснения зависимости  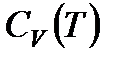необходимо использовать квантовые представления. С точки зрения квантовой теории теплоемкости тот факт, что некоторые вещества (алмаз, бор и др.) не подчиняются закону Дюлонга и Пти даже при комнатных температурах, объясняется именно тем, что у этих веществ характеристическая температура Дебая настолько высока, что комнатная температура должна считаться низкой температурой. Так, если для серебра  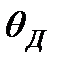= 210 °С, для алюминия  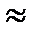400 °С, для свинца  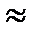90 °С, то характеристическая температура Дебая для алмаза равна 2000 °С. Вместе с тем, если температуру тела нормировать на температуру Дебая, то ход температурных зависимостей теплоемкости различных веществ, отнесенной к числу атомов в молекуле данного вещества n, весьма близок (рис. 2).

В табл. 2-7.1 приведены численные значения температуры Дебая для некоторых простых и сложных кристаллических соединений.

Таблица.2-7.1.