Баллон с распределительным краном, U- образный манометр, насос секундомер. Схема установки предоставлена на рис. 2-6.1.
Установка состоит из стеклянного баллона Б, который может быть соединен с помощью распределительного крана К либо c атмосферой, либо с насосом Н и манометром М. Водяной U -образный манометр измеряет разность между давлением в баллоне и атмосферным давлением в мм. водного столба.
| 1 |
| 5 |
| Рис. 2-6.2. Диаграмма процессов в газе |
| 7 |
| 3 |
| P |
| T0=const |
| P0, V0 ,T0 |
| 6 |
| 4 |
| 2 |
| V |
| Накачиваем |
| Открыли кран |
Р1
Р2
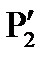 P0
P0
|
| 7 |
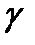 для газа, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, представленных на
для газа, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, представленных на 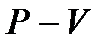 - диаграмме рис. 2-6.2. Обозначим через
- диаграмме рис. 2-6.2. Обозначим через 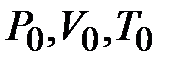 исходные величины термодинамических параметров газа в баллоне. Сначала в баллон накачивается воздух (процесс 1-2). При этом газ в баллоне сжимается и нагревается. После изохорического остывания до начальной комнатной температуры
исходные величины термодинамических параметров газа в баллоне. Сначала в баллон накачивается воздух (процесс 1-2). При этом газ в баллоне сжимается и нагревается. После изохорического остывания до начальной комнатной температуры 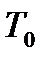 газ имеет некоторое давление
газ имеет некоторое давление 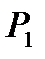 (процесс 2-3). Затем краном соединяют баллон с атмосферой, и газ, адиабатически расширяясь, охлаждается (процесс 3-4), его давление падает до величины
(процесс 2-3). Затем краном соединяют баллон с атмосферой, и газ, адиабатически расширяясь, охлаждается (процесс 3-4), его давление падает до величины 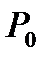 , а температура - до величины
, а температура - до величины 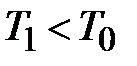 . В момент достижения давления
. В момент достижения давления 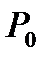 кран К перекрывается и газ изохорически нагревается до комнатной температуры (процесс 4-5). В конечном состоянии давление газа
кран К перекрывается и газ изохорически нагревается до комнатной температуры (процесс 4-5). В конечном состоянии давление газа 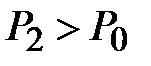 , а температура равна
, а температура равна 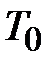 .
.
Масса газа, находящегося в баллоне, в начальном состоянии выражается соотношением 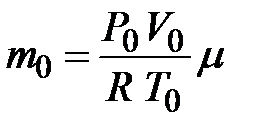 .
.
Нетрудно видеть, что в течение всех рассмотренных термодинамических процессов масса газа в баллоне больше или равна 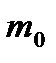 .
.
Назовем массу 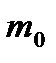 рабочей массой газа, эта масса остается все время в баллоне. Накачиваемый и выпускаемый из баллона газ служит лишь для сжатия и расширения рабочей массы газа.
рабочей массой газа, эта масса остается все время в баллоне. Накачиваемый и выпускаемый из баллона газ служит лишь для сжатия и расширения рабочей массы газа.
Введем обозначения 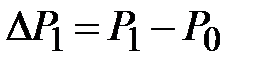 и
и 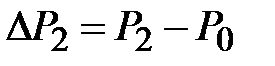 . Тогда величина
. Тогда величина 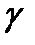 оценивается по формуле
оценивается по формуле
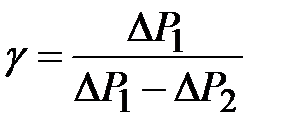 . .
| (2-6.2) |
Вывод выражения (2-6.2 ) приводится в Приложении.
Измерив значения 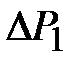 и
и 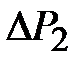 , можно было бы рассчитать величину
, можно было бы рассчитать величину 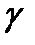 . Однако при таком методе расчета необходимо выполнение следующих условий:
. Однако при таком методе расчета необходимо выполнение следующих условий:
1. При адиабатическом расширении (процесс 3-4) кран баллона должен быть перекрыт в момент, когда давление в баллоне станет равным 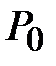 ;
;
2. Время выпуска газа должно быть достаточно мало, так, чтобы теплообменом с окружающим воздухом можно было пренебречь.
Практически эти условия выполнить трудно, что приводит к ошибкам в определении 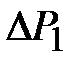 и
и 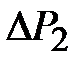 , и, следовательно, в оценке
, и, следовательно, в оценке 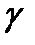 .
.
После открытия крана (процесс 3-4) давление в баллоне со временем уменьшается по экспоненциальному закону и через 0.1 секунды отличается от 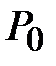 не более чем на 1%.
не более чем на 1%.
Однако вручную открыть кран на 0,1 секунды трудно, практически время это оказывается значительно больше. Рассмотрим влияние времени, в течение которого после достижения давления 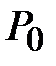 кран К еще остается открытым, не влияет на результат опыта.
кран К еще остается открытым, не влияет на результат опыта.
Предположим, что после достижения давления 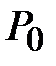 кран остается открытым еще некоторое время
кран остается открытым еще некоторое время 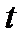 , за это время за счет теплообмена со стенками баллона и расширения газа происходит изобарический нагрев газа (процесс 4-6). После того как кран закрывается (точка 6), происходит изохорический нагрев газа (процесс 6-7), давление в баллоне достигает величины
, за это время за счет теплообмена со стенками баллона и расширения газа происходит изобарический нагрев газа (процесс 4-6). После того как кран закрывается (точка 6), происходит изохорический нагрев газа (процесс 6-7), давление в баллоне достигает величины 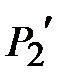 (точка 7). Точка 7 лежит на той же изотерме, что точки 3 и 5, но
(точка 7). Точка 7 лежит на той же изотерме, что точки 3 и 5, но 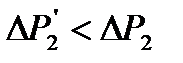 Очевидно, что
Очевидно, что 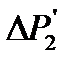 зависит от времени выхода газа из баллона, и значение
зависит от времени выхода газа из баллона, и значение 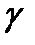 , рассчитанное по формуле (2-6.2), будет иметь погрешность.
, рассчитанное по формуле (2-6.2), будет иметь погрешность.
Рассмотрим детальнее процесс нагревания газа на участке (4-6). За счет теплопроводности через стенки баллона за время 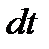 газ будет получать количество теплоты
газ будет получать количество теплоты
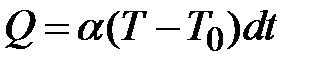 ,
,
где 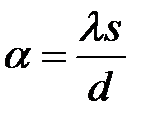 . Здесь
. Здесь 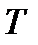 - температура газа в баллоне,
- температура газа в баллоне, 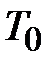 - температура окружающего воздуха,
- температура окружающего воздуха, 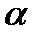 - коэффициент теплопроводности стекла,
- коэффициент теплопроводности стекла, 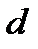 и
и 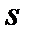 - толщина и площадь стенок баллона соответственно.
- толщина и площадь стенок баллона соответственно.
Уравнение баланса энергии для газа, находящегося в баллоне, может быть записано в виде
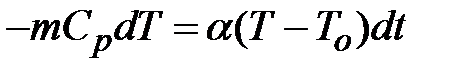 . .
| (2-6.3) |
Разделив переменные и подставив 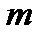 из уравнения Менделеева-Клапейрона, получим
из уравнения Менделеева-Клапейрона, получим
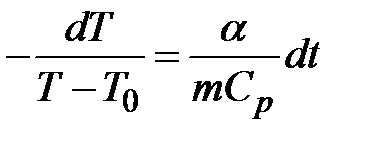 или
или 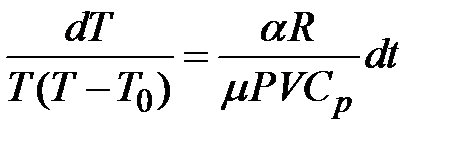 .
.
Последнее выражение можно представить как
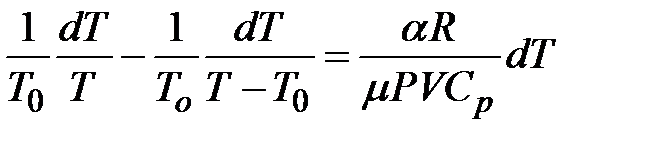 , (2-6.4)
, (2-6.4)
его интегрирование дает:
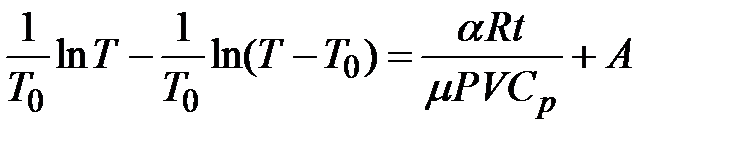 ,
,
где 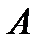 постоянная интегрирования.
постоянная интегрирования.
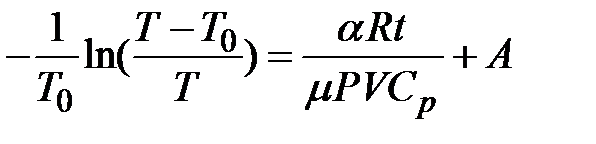 ,
,
откуда
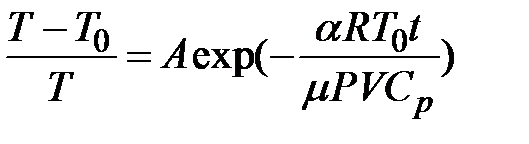 . .
| (2-6.5) |
Обозначим температуру газа в баллоне в момент 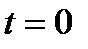 (точка 4) через
(точка 4) через 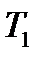 , а
, а 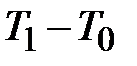 через
через 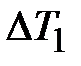 , тогда постоянная интегрирования А будет равна
, тогда постоянная интегрирования А будет равна 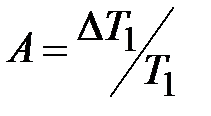 .
.
Окончательно соотношение (2-6.5) примет вид
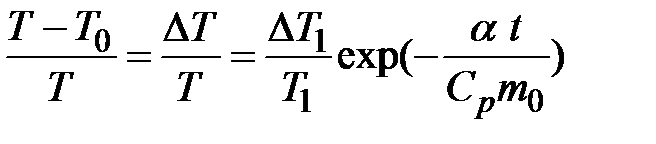 , ,
| (2-6.6) |
где учтено выражение (1) и то обстоятельство, что точки 3 и 7 лежат на одной изотерме.
После того как в момент времени t кран К перекрывается, нагрев газа в баллоне также продолжается, но уже изохорически. Давление газа в конце концов достигает величины 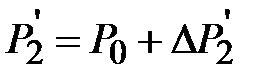 . Для изохорического процесса
. Для изохорического процесса 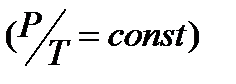 (участок 6-7) имеем
(участок 6-7) имеем
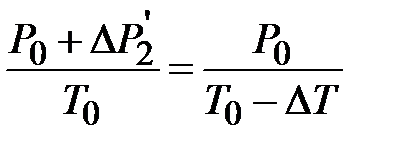 или или 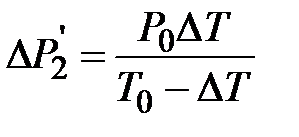 . .
| (2-6.7) |
С другой стороны, из уравнения адиабаты (участок 3-4) имеем:
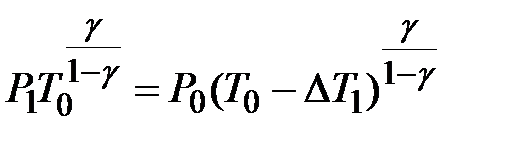 .
.
Воспользуемся формулой бинома Ньютона, пренебрегая членами второго порядка малости:
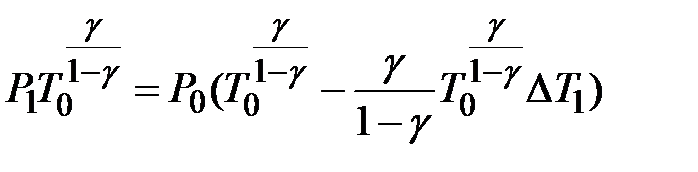 .
.
И учитывая, что 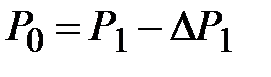 , получим
, получим
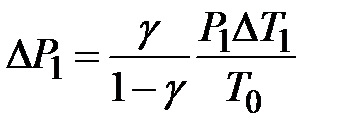 и и 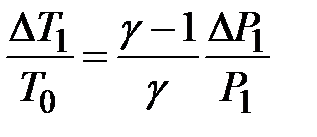 . .
| (2-6.8) |
Решая совместно уравнения (2-6.6),(2-6.7),( 2-6.8) и снова пренебрегая слагаемыми второго порядка малости, получим
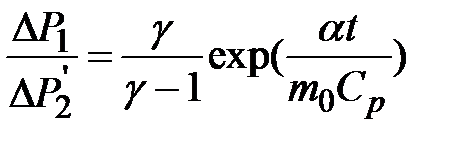 . .
| (2-6.9) |
Это уравнение учитывает как теплообмен с окружающей средой, так и уход части газа из баллона в процессе нагрева. Уравнение позволяет найти 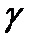 по измеренным при разных величинах
по измеренным при разных величинах 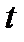 значениями
значениями 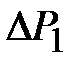 и
и 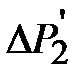 . Прологарифмируем выражение (2-6.9):
. Прологарифмируем выражение (2-6.9):
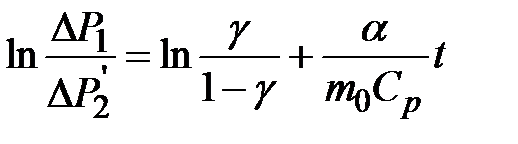 .
.
График зависимости 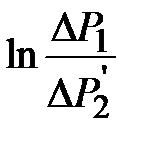 от t является линейной функцией. Если экстраполировать этот график по t = 0, то он будет отсекать на оси ординат отрезок
от t является линейной функцией. Если экстраполировать этот график по t = 0, то он будет отсекать на оси ординат отрезок
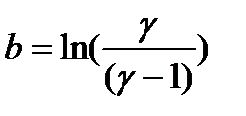 . .
| (2-6.10) |
Потенцируя выражение (10) и преобразуя его, получим
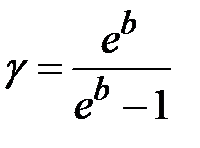 . .
| (2-6.11) |
Порядок выполнения работы
Закрыть кран и накачать воздух в баллон (процесс1-2) так, чтобы величина 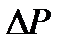 , показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины
, показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины 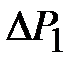 . Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра
. Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра 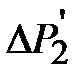 . Аналогично провести измерения для времени выдержки t =50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
. Аналогично провести измерения для времени выдержки t =50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
Обработка результатов
| b |
| 0 |
| 10 |
| 20 |
| t, с |
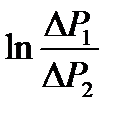
|
Рис. 3. График зависимости 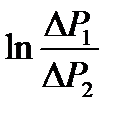 от t от t
|
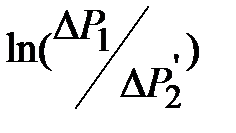 от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину
от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину 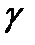 по формуле (2-6.11).
по формуле (2-6.11).
В данной работе зависимость  от t и оценка величины
от t и оценка величины 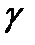 статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе).
статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе).
Контрольные вопросы и задания
1. Что называется теплоемкостью газа?
2. Какова размерность этой физической величины?
3. Что понимается под удельной и малярной теплоемкостями газа?
4. Как они связаны между собой? Какова связь между 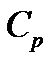 и
и  и числом степеней свободы молекул газа?
и числом степеней свободы молекул газа?
5. Получите уравнение Роберт Майера. Сколько степеней свободы имеют молекулы газов Нe, Н2, СО2?
6. Какие это степени свободы? В каком газе показатель адиабаты 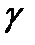 имеет наибольшее значение – N2, Нe, СН4?
имеет наибольшее значение – N2, Нe, СН4?
7. Почему в данном эксперименте целесообразно использовать сосуд возможно большего диаметра?
8. Получите уравнение адиабаты в перемененных PT и TV. Какие явления нарушают адиабатичность расширения газа?
9. Как повлияет на ход эксперимента наличие паров воды в воздухе?
Список рекомендуемой литературы
1. Матвеев А.Н. Молекулярная физика. М. : Высш. шк., 1988.
2. Булкин П.С., Попова И.И. Общий физический практикум. М. : МГУ, 1988.
3. Основы физики. Курс общей физики. Т.2. Квантовая и статистическая физика / Под. ред. Ю.М. Ципенюка. М. : Физ.-мат. лит., 2001.
Лабораторная работа № 2-7
Теплоемкость твердых тел
Дата: 2019-03-05, просмотров: 432.