Найти экстремумы функции двух переменных самостоятельно, а затем посмотреть решение

Пример 2. Найти экстремумы функции двух переменных

.

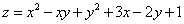Посмотреть правильное решение и ответ.

Нет времени вникать в решение? Можно заказать работу!

Третий пример - на десерт, так как в нём только одна критическая точка.

Пример 3. Найти экстремумы функции двух переменных .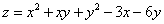

Шаг 1. Находим частные производные:

.

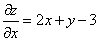
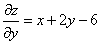Шаг 2. Составляем систему уравнений из равенств этих производных нулю:

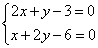
Решаем систему уравнений:

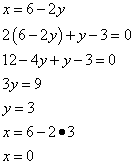
Таким образом, получили критическую точку 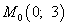- точку возможного экстремума.

Шаг 3. Находим частные производные второго порядка

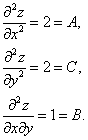
Шаг 4. Находим определитель 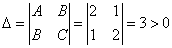, т. е. в найденной критической точке есть экстремум, причём так как 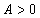, то это минимум.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:

.

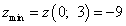Найти экстремумы ещё одной функции двух переменных самостоятельно, а затем посмотреть решение

Наибольшее и наименьшее значения функции двух переменных в замкнутой области.

Пусть функция z=f(x,y) определена и непрерывна в некоторой ограниченной замкнутой области D. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.

Алгоритм поиска наибольшего и наименьшего значений функции z=f(x,y) в замкнутой области D.

1. Найти критические точки функции z=f(x,y), принадлежащие области D. Вычислить значения функции в критических точках.

2. Исследовать поведение функции z=f(x,y) на границе области D, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.

3. Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.

Что такое критические точки? показать\скрыть

Пример №1

Найти наибольшее и наименьшее значения функции z=x2+2xy−y2−4x в замкнутой области, ограниченной линиями x=3, y=0 и y=x+1.

Решение

Будем следовать указанному выше алгоритму, но для начала разберёмся с чертежом заданной области, которую обозначим буквой D. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая x=3проходит через точку (3;0) параллельно оси ординат (оси Oy). Прямая y=0 – это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой y=x+1 найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо x парочку произвольных значений. Например, подставляя x=10, получим: y=x+1=10+1=11. Мы нашли точку (10;11), лежащую на прямой y=x+1. Однако лучше отыщем те точки, в которых прямая y=x+1 пересекается с линиями x=3 и y=0. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой y=x+1 и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая y=x+1пересекает прямую x=3 в точке (3;4), а прямую y=0 – в точке (−1;0). Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.

Как были получены точки (3;4) и (−1;0)? показать\скрыть

Всё готово для построения чертежа, который будет иметь такой вид:

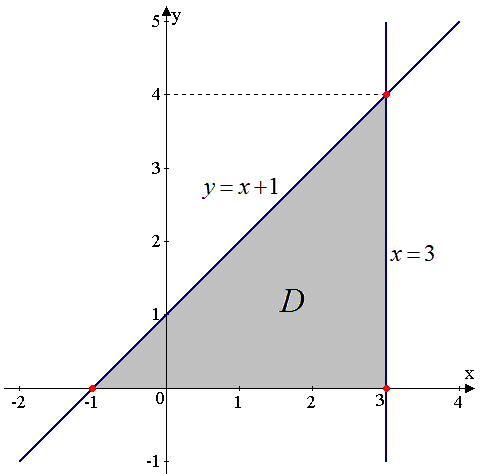
Вот теперь перейдём к первому шагу алгоритма. Найдём частные производные первого порядка:

∂z∂x=2x+2y−4;∂z∂y=2x−2y.

Заметьте, что найденные производные первого порядка существуют для всех значений x и y. Т.е. нету точек, в которых хотя бы одна производная не существует. Попробуем отыскать точки, в которых обе частные производные равны нулю (стационарные точки):

{2x+2y−4=0;2x−2y=0.{x+y=2;x−y=0.

Мы получили систему линейных алгебраических уравнений. Для решения таких систем можно применить, например, метод Крамера. Однако в данном случае можно поступить попроще. Из второго уравнения имеем: y=x. Подставляя y=x в первое уравнение, получим: x+x=2, 2x=2, x=1. Так как x=1, то y=x=1. Итак, (1;1) – единственная стационарная точка функции z.

Однако недостаточно просто найти стационарные точки. Нужно выбрать те из них, которые принадлежат области D. В нашем случае точка (1;1) принадлежит этой области. Обозначим эту точку как M1(1;1). Вычислим значение функции в этой точке:

z1=z(M1)=12+2⋅1⋅1−12−4⋅1=−2.

А почему точка (1;1) принадлежит области D? показать\скрыть

Теперь настал черёд исследовать поведение функции на границе области, т.е. переходим ко второму шагу алгоритма. Начнём с прямой y=0.

Прямая y=0 (ось абсцисс) ограничивает область D при условии −1≤x≤3. Подставим y=0 в заданную функцию z(x,y)=x2+2xy−y2−4x. Полученную в результате подстановки функцию одной переменной x обозначим как f1(x):

f1(x)=z(x,0)=x2+2x⋅0−02−4x=x2−4x.

Теперь для функции f1(x) нужно найти наибольшее и наименьшее значения на отрезке −1≤x≤3. Отыщем производную этой функции и приравняем её к нулю:

f′1(x)=2x−4;2x−4=0;x=2.

Значение x=2 принадлежит отрезку −1≤x≤3, поэтому к списку точек добавим ещё и M2(2;0). Кроме того, вычислим значения функции z на концах отрезка −1≤x≤3, т.е. в точках M3(−1;0) и M4(3;0). Кстати, если бы точка M2 не принадлежала рассматриваемому отрезку, то, разумеется, значение функции z в ней вычислять не было бы надобности.

Итак, вычислим значения функции z в точках M2, M3, M4. Можно, конечно, подставлять координаты данных точек в исходное выражение z=x2+2xy−y2−4x. Например, для точки M2 получим:

z2=z(M2)=22+2⋅2⋅0−02−4⋅2=−4.

Однако вычисления можно немного упростить. Для этого стоит вспомнить, что на отрезке M3M4 имеем z(x,y)=f1(x). Распишу это подробно:

z2=z(M2)=z(2,0)=f1(2)=22−4⋅2=−4;z3=z(M3)=z(−1,0)=f1(−1)=(−1)2−4⋅(−1)=5;z4=z(M4)=z(3,0)=f1(3)=32−4⋅3=−3.

Разумеется, что в столь подробных записях обычно нет нужды, и все вычисления в дальнейшем станем записывать покороче:

z2=f1(2)=22−4⋅2=−4;z3=f1(−1)=(−1)2−4⋅(−1)=5;z4=f1(3)=32−4⋅3=−3.

Теперь обратимся к прямой x=3. Эта прямая ограничивает область D при условии 0≤y≤4. Подставим x=3 в заданную функцию z. В результате такой подстановки мы получим функцию f2(y):

f2(y)=z(3,y)=32+2⋅3⋅y−y2−4⋅3=−y2+6y−3.

Для функции f2(y) нужно найти наибольшее и наименьшее значения на отрезке 0≤y≤4. Отыщем производную этой функции и приравняем её к нулю:

f′2(y)=−2y+6;−2y+6=0;y=3.

Значение y=3 принадлежит отрезку 0≤y≤4, поэтому к найденным ранее точкам добавим ещё и M5(3;3). Кроме того, нужно вычислить значение функции z в точках на концах отрезка 0≤y≤4, т.е. в точках M4(3;0) и M6(3;4). В точке M4(3;0) мы уже вычисляли значение z. Вычислим значение функции z в точках M5 и M6. Напомню, что на отрезке M4M6 имеем z(x,y)=f2(y), поэтому:

z5=f2(3)=−32+6⋅3−3=6;z6=f2(4)=−42+6⋅4−3=5.

И, наконец, рассмотрим последнюю границу области D, т.е. прямую y=x+1. Эта прямая ограничивает область D при условии −1≤x≤3. Подставляя y=x+1 в функцию z, будем иметь:

f3(x)=z(x,x+1)=x2+2x⋅(x+1)−(x+1)2−4x=2x2−4x−1.

Вновь мы получили функцию одной переменной x. И вновь нужно найти наибольшее и наименьшее значения этой функции на отрезке −1≤x≤3. Отыщем производную функции f3(x) и приравняем её к нулю:

f′3(x)=4x−4;4x−4=0;x=1.

Значение x=1 принадлежит отрезку −1≤x≤3. Если x=1, то y=x+1=2. Добавим к списку точек ещё и M7(1;2) и выясним, чему равно значение функции z в этой точке. Точки на концах отрезка −1≤x≤3, т.е. точки M3(−1;0) и M6(3;4), были рассмотрены ранее, значение функции в них мы уже находили.

z7=f3(1)=2⋅12−4⋅1−1=−3.

Второй шаг решения закончен. Мы получили семь значений:

z1=−2;z2=−4;z3=5;z4=−3;z5=6;z6=5;z7=−3.

Обратимся к третьему шагу алгоритма. Выбирая наибольшее и наименьшее значения из тех чисел, что были получены в третьем пункте, будем иметь:

zmin=−4;zmax=6.

Задача решена, осталось лишь записать ответ.

Ответ: zmin=−4;zmax=6.