В курсе математики начальных классов нашли отражение все свойства умножения: коммутативные (переместит-е), ассоциативное (сочетат-е (a + b) + c = a + (b + c)) и дистрибутивное (распределит-е ( a + b ) • c = a • c + b • c).

      Коммутативность умножения представлена в учебниках как переместительное свойство; от перестановки множителей значение произведения не изменяется. При знакомстве с этим свойством умножения учащиеся выполняют задания на соотнесение рисунка с математической записью и на сравнение числовых выражений, в которых переставлены множители. Усвоение формулировки переместительного свойства умножения обычно не вызывает затруднений, хотя многие дети и ошибаются, называя множители слагаемыми, а произведение — суммой. Это объясняется не только тем, что они не усвоили названий компонентов и результатов действий умножения и сложения, но и является следствием формального подхода к изучению самого переместительного свойства, когда дети абстрагируются от конкретных ситуаций, связанных со смыслом умножения.

    Сочетательное свойство умножения Введение в программу начального курса математики сочетательного свойств умножения позволяет познакомить учащихся с новыми вычислительными приемами, с помощью которых они могут находить рациональные способы вычислений. Это свойство может изучаться как во 2 и так в 3 классе, все зависит от логики построения курса обучения.
Например: в учебнике М. И. Моро изучение сочетательного свойства умножения, которое представлено как умножение числа на произведении, предшествует изучению темы «Умножение на числа, оканчивающиеся нулями». Это позволяет познакомить учащихся с новым способом действия при выполнении устных вычислений для данного случая умножения и обосновать ту форму записи «в столбик», которая используется при умножении чисел, оканчивающихся нулями. В учебнике есть образцы умножения, анализируя образцы учащиеся приходят к выводу, что умножать на число на произведение можно 3 способами: а) 5* (2*3)= 5*6=30                   б) 5* (2*3)= (5*2)*3= 10*3= 30           в) 5* (2*3)= (5*3)*2= 15*2= 30

        Распределительное свойство Знакомство с распределительным свойством так же зависит от логики построения курса обучения. Есть 2 варианта:

1 вариант. Сам термин «Распределительное свойство» не вводится, а рассматривается как 2 правила: а) умножение суммы на число б) умножение числа на сумму
    Изучение этих правил разведено по времени, т.к. первое правило лежит в основе вычислительного приема умножения двузначного числа на однозначное (в пределах 100), а второе правило вводится для разъяснения способа действия при умножении двузначного числа на двузначное «в столбик». Этот вариант используется в учебниках М. И. Моро. Пример: Вычисли разными способами значения выражений: 6*(5*4); 80*(1+6); 20*(2+3).
2 вариант. Учащихся знакомят с названием свойства и усваивают его содержание в процессе выполнения различных заданий. Этот вариант используется в учебниках Н. Б. Истоминой. Пример: Вставь знаки <, > или =, чтобы получить верные записи: (5+2)*3 … 5*3+2*3;     (6+3)*4 … 6*4+3*4.

Методика изучения долей в начальном курсе математики.

Ознакомление с долями и дробями традиционно начинается в 3 классе. С этой целью предусматривается ознакомить детей с долями, их записью, научить сравнивать дроби, решать задачи на нахождение доли числа и числа по доле; в 4 классе ознакомить с дробями, их записью, научить сравнивать дроби, научить решать задачи на нахождение дроби числа

Работа над данной темой ведется в 2 этапа.

Ознакомление с долями.

Ознакомить детей с долями - значит сформировать у них конкретные представления о долях, то есть научить детей образовывать доли практически. Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть

Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги;

Познакомить детей с долями можно таким образом. У каждого из учащихся и у учителя по несколько одинаковых кругов, прямоугольников. Учитель: «Возьмите два одинаковых круга. Один из них разделите на две равные части (показывает, как надо перегнуть и как разрезать круг). Это целый круг, а это половина круга, иначе говоря, одна вторая доля круга. Сколько вторых долей в целом круге? (2) . Покажите их.

  Доли записывают с помощью двух чисел. Одна вторая доля круга, квадрата обозначается так: 1/2. Число 2 показывает, что круг, квадрат или другая фигура (предмет), разделена на 2 равные части, а число 1 показывает, что взяли одну такую часть.

Так же образуются доли 1/4, 1/8, 1/3, 1/6, 1/5, 1/10 и др. При этом учащиеся должны уяснить, что для получения например, 1/5 отрезка (прямоугольника, бумажной полоски) надо данный отрезок (прямоугольник , полоску) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке 5 пятых долей, что одна пятая доля записывается так: 1/5, что в этой записи число 5 обозначает, на сколько равных частей разделен отрезок, а число 1, - что взята одна такая часть. Для закрепления этих знаний и умений учащимся предлагают различные упражнения.

Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. В этом их основное назначение.

 В 3 классе рассматривается только простые задачи, а в 4 классе они включаются в составные.

Ознакомление с дробями.

Образование дробей, как и образование долей рассматривается с помощью наглядных пособий.

Ознакомление начинается с упражнений вида: «Разделите круг на 4 равные части. Как назвать каждую такую часть? Запишите. Покажите три четвертые доли. Вы получили дробь - три четвертых. Кто сможет записать эту дробь? Что показывает число 4 (на сколько равных частей разделили круг)? Что показывает число 3 (сколько таких частей взяли)?

Конкретный смысл дроби очень ярко раскрывается при решении задач на нахождение доли числа («В классе 32 ученика. Из них 1/4 играют в хоккей. Сколько хоккеистов в классе?»)

В дальнейшем, решая такие задачи, учащиеся должны самостоя-тельно выполнять подобные рассуждения. Например, надо узнать, сколько минут в 3/4 ч. Ученик рассуждает: «Найду, сколько минут составляет 1/4 ч, для этого 60 разделю на 4, получится 15; теперь найду, сколько минут в 3/4 ч, для этого 15 умножу на 3, получится 45; значит, 3/4 ч -- это 45 мин».

Помним, что чем больше долей, тем меньше каждая доля.

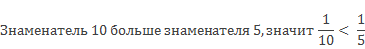
вывод: из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше