Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: {\displaystyle S=\pi r^{2}} 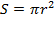Формула проста: чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.

1.Находим по радиусу:

Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.

число Пи. Это число обозначается греческой буквой {\displaystyle \pi } и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр.

В нашем примере (r = 6 см) площадь вычисляется так:

· {\displaystyle S=\pi r^{2}}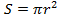

· {\displaystyle S=\pi 6^{2}}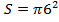

· {\displaystyle S=36\pi } 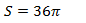или {\displaystyle S=36(3,14)=113,04}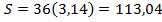

2.2

2. Находим по диаметру: аналогично с первым примером, только сначала находим радиус – диаметр делим пополам.

3. По длине окружности, где С- длина окружности.

Применяем формулу : S=C в квадрате/ 4Пи
4. По площади сектора круга и углу. Применяем формулу: S круга = S сектора круга умножить на частное 360/ С (где С – угол)

.

Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:

1. равные тела имеют равные объемы;

2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.

Будем объем тела Q обозначать V(Q).

Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е³. Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е³, которое называют численным значением объема при данной единице объема.

Свойства численных значений объема

1. Если тела равны, то равны и численные значения их объемов: Q₁ = Q₂

2. Если тело Q состоит из тел Q₁, Q₂,…, Q_n, то численное значение объема тела равно сумме численных значений объемов этих тел.

3. При замене единицы измерения объема численное значение объема увеличивается (уменьшается) во столько раз, во сколько раз уменьшается (увеличивается) единица объема.

Основная единица измерения объема – кубический метр.

В начальной школе рассматривается объем прямоугольного параллелепипеда.

Рассмотрим случай, когда длина, ширина и высота выражены натуральными числами. Если стороны основания равны а и b, то на это основание можно уложить а ∙ b единичных кубиков. Так как в высоту укладывается с таких слоев, то объем параллелепипеда вычисляется по формуле V = а ∙ b∙ с.

Таким образом объем прямоугольного параллелепипеда равен произведению трех его измерений.

В начальной школе изучается также такая величина, как емкость. Она рассматривается как объем сыпучих и жидких тел. Единица измерения емкости – литр. 1 л = 1 дм³.