Методика обучения математике как науке. Предмет и задачи, связь с другими науками

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ОТВЕТЫ

«МЕТОДИКА ПРЕПОДАВАНИЯ ПРЕДМЕТНЫХ ОБЛАСТЕЙ «МАТЕМАТИКА», «ОКРУЖАЮЩИЙ МИР»

Уметь

· использовать математические представления для описания окружающего мира (предметов, процессов, явлений) в количественном и пространственном отношении;

· производить вычисления для принятия решений в различных жизненных ситуациях;

· читать и записывать сведения об окружающем мире на языке математики;

· формировать основы рационального мышления, математической речи и аргументации;

· работать в соответствии с заданными алгоритмами;

· узнавать в объектах окружающего мира известные геометрические формы и работать с ними;

· вести поиск информации ,преобразовать её в удобные для изучения и применения формы.

Начальный курс это исходная база для курса математики, поэтому

включает: арифметику целых неотрицательных чисел и основных величин, элементы алгебры и геометрии.

Главное содержание составляет арифметический материал, элементы алгебры и геометрии органически связываются с арифметическим материалом. Арифметический материал вводится концентрически:

1. Нумерация первого десятка;

2. Нумерация чисел в пределах 100;

3. Нумерация чисел в пределах 1000;

4. Нумерация многозначных чисел.

В тесной связи с арифметическим материалом изучаются: величины,

дроби, алгебраический и геометрический материал.

Кроме пяти традиционных содержательных разделов:

Числа и величины

Арифметические действия над числами

Работа с текстовыми задачами

Пространственные отношения. Геометрические фигуры.

Геометрические величины.

в современных программах есть шестой содержательный раздел:

Работа с информацией.

Методика обучения младших школьников математике в дочисловой период.

У детей в дочисловой период Урок: 30 минут

Особенности детей:

-плохо развита мелкая мускулатура

-быстро устают

- неустойчивость внимания

- слабо развито мышление

-слабо развита конкретизация.

На уроках дочислового периода надо систематизировать и пополнять знания, умения и навыки, которыми обладают дети, дать те знания, которые необходимы для изучения нумерации.

Задачи изучения темы.

1. Должно быть отработано умение вести счет различных объектов (предметов, звуков, движений). Дети должны усвоить, что, отвечая на вопрос «сколько?», предметы можно считать в любом порядке, а на вопрос «который по счету?» - в определенном, указанном порядке.

На уроках дочислового периода дети считают хором, по цепочке, индивидуально, по представлению (Сколько этажей в школе? Сколько героев в сказке «Репка»?)

Дети знакомятся с аксиомой счета - считать можно в любом порядке (слева направо, справа налево, вразброс, соблюдая при этом следующие требования:

- не пропускать при счете ни один предмет;

- ни один предмет не считать дважды.

2. На основе многочисленных практических упражнений дети должны научиться сравнивать две группы предметов, выясняя, в которой из них содержится больше (меньше) предметов, или же убедиться в том, что они содержат равное число предметов.

Сравнение ведется без счета – образованием пар предметов, а также с помощью счета предметов. Сравнение ведется в обе стороны: если в одной из сравниваемых групп предметов больше, то в другой - на столько же меньше. Решается задача по уравниванию количества предметов в группах (двумя способами: добавляют недостающие предметы, убирают «лишние»)

3. На этих уроках уточняются пространственные представления: дети должны научиться различать, например, на странице учебника верхнюю и нижнюю картинку, левую и правую страницы учебника, большой рисунок и маленький, научиться понимать выражения «выше», «ниже», «направо», «справа налево» и т.п.

4. Дети должны научиться понимать выражения, отражающие порядковые отношения: «следовать за», «стоять (идти) перед», «находиться между».

Продолжительность дочислового периода- приблизительно неделя (5-6 уроков). На первой неделе занятий дети учатся работать со счетным материалом, с книгой и в тетради. Формирование соответствующих умений и навыков на уроках дочислового периода только начинается, оно будет продолжено на уроках по теме «Нумерация».

Помимо основных видов деятельности, дети группируют предметы по разным признакам, в т.ч. по форме, цвету, размеру. Вводятся сложение и вычитание на множествах, переместительное свойство умножения.

Задачи:

- познакомить с образованием числа первого десятка

- научить обозначать число цифрой

- соотносить количество, число и цифру

- счет в пределах 10

- определить место числа в ряду чисел

- выполнять сравнение

- изучить состав числа

Изучение чисел происходит последовательно от 1, 2 до 10, затем знакомятся с числом 0. При изучении этой темы дети должны уяснить образование чисел первого десятка, обозначение их на письме, положение в натуральном ряду чисел, состав чисел и научиться выполнять сложение и вычитание вида а+1, а-1. В соответствии с этим подходом последовательно рассматриваются отрезки натурального ряда чисел 1 2, 1 2 3, 1 2 3 4 , …1 2…10.

Проведя такие рассуждения 3-4 раза. Только с другими предметами. Выясняют, что число 4 больше числа 3 на 1. а число 3 меньше числа 4 на 1. Таким образом, число 4 стоит в ряду чисел после 3. Получая следующее число. Учащиеся знакомятся с соответствующей цифрой и учатся её писать. Такое одновременное введение числа и цифры затрудняет осознание различий между этими понятиями.

Число 0 появляется как численность множества, из которого последовательно убираются все элементы.

Формирование представлений о каждом числе, включая виды деятельности:

1. Повторение ранее изученных чисел

2. Знакомство с образованием нового числа (путем присчитывания 1 к предыдущему числу)

3. Пересчет предметов с интонацией выделять число последнего (последнее количество предметов)

4. Обозначать число цифрой

5. Обучение написания чисел

6. Демонстрация образования числа 2 способами: прибавление к предыдущему, вычитание из последующего

7. Подбор к данному числу соответствующего количества предметов

8. Управление в сравнении множеств

9. Определение места числа в натуральном ряду

10. Знакомство с составом числа

11. Выполнение сложения чисел из которых состоит число и вычитание из данного числа

12. Выполнение практических заданий на + и –

Наглядность:

- кассы

- предметы для счета

- карточки

- карточки с образцом

- таблицы состава числа

- карточки арифметических задач

0 – 9

Содержание геометрического материала и ознакомление с величинами и их измерением в 1 классе.

Согласно государственным стандартам обучения в начальных классах общеобразовательной школы одной из целей начального математического образования является формирование у младших школьников достаточно полной системы пространственных представлений, ознакомление учащихся с различными геометрическими фигурами и некоторыми их свойствами, с простейшими чертежами и измерительными приборами.

Главная задача заключается в развитии у учащихся пространственных представлений, умения наблюдать, сравнивать, обобщать и абстрагировать; формировании у школьников практических умений строить, рисовать, моделировать и конструировать геометрические фигуры от руки и с помощью простых чертежных инструментов.

В начальном курсе математики учащихся формируют представление и понятие о геометрические фигуры на плоскости, их существенные признаки и свойства; учат распознавать геометрические фигуры в пространстве и их элементы, сопоставлять образы геометрических фигур с окружающими предметами.

Эта цель последовательно реализуется путем решения следующих задач:

· формирование геометрических представлений об образах геометрических фигур, их элементов, отношений между фигурами и их элементами;

· выработка практических умений и навыков в измерениях и построении простейших геометрических фигур с помощью чертежных инструментов;

· развитие пространственных представлений, воображения и пространственного мышления учащихся;

· обогащение математического словарного запаса, развитие речи учащихся.

Согласно традиционной программе обучения математике в начальной школе, в 1 классе уточняются пространственные представления учащихся. С первых дней обучения ребенка в школе на уроках математики рассматриваются понятия «вверху», «внизу», «выше», «ниже», «слева», «справа», «левее», «правее», «перед», «за», «между», «рядом», а также направления движения «слева направо», «справа налево», «сверху вниз», «снизу вверх». Уже в процессе изучения нумерации чисел первого десятка учащиеся знакомятся с точкой, прямой и кривой линиями, отрезком, ломаной, многоугольником, углом, вершиной и сторонами многоугольника. Здесь же школьники изучают геометрическую величину «длина отрезка», единицы измерения длины - сантиметр, дециметр, и соотношения между ними.

В 1 классе, с самых первых уроков, обучающиеся знакомятся с такими геометрическими фигурами как: квадрат, прямоугольник, треугольник, круг. Разрезание этих фигур на части и составление новых фигур из полученных частей помогает им уяснить инвариантность площади, способствует развитию комбинаторных способностей.

Кроме того, в 1 классе учащиеся знакомятся с такими понятиями как: область, граница, сеть линий и др. Эти понятия имеют топологический характер, поэтому область их применения весьма обширная. Вместе с тем дети без труда их усваивают, т.к. топологические представления у них развиваются раньше, чем аффинные и метрические. Сравнительно рано, в 1классе, появляются простейшие пространственные образы: куб, параллелепипед, цилиндр, пирамида, шар, конус.

Содержание изучаемого учащимися материала в концентре «Сотня».

Задачи:

1. Познакомить обучающихся с новой счетной единицей «десяток».

2. Показать, как образуются числа из десятков и единиц. Ввести понятие «разряд», разъяснить, что двузначные числа имеют два разряда: единицы и десятки.

3. Научить читать и записывать числа, показывать способ записи чисел на основе закона поместного значения цифр.

4. Добиться сознательного разделения понятий «цифра»и «число».Довести до сознания обучающихся тот факт, что значение цифры в записи числа зависит от места, на котором она стоит. Добиться усвоения понятий и формирования умения пользоваться терминами: однозначное, двузначное число.

5. Добиться усвоения натуральной последовательности чисел в пределах 100.

6. Научить считать в пределах ста десятками и по одному.

7. Сформировать умение складывать и вычитать числа на основе знания разрядного состава числа (20+5; 25-5) и суммы удобных слагаемых (16 +1; 16 – 1).

8. Научить сравнивать числа, опираясь на различные знания по нумерации, а также на основе сравнения разряда десятков.

9. В тесной связи с изучением нумерации двузначных чисел познакомить детей с единицами длины.

Изучение нумерации в концентре 100 проходит в два этапа: 1) от 11 до 20; 2) от 21 до 100, так как имеются различия в устной и письменной нумерации в этих числах

Письменная нумерация: 1 3 3 1

Записываются числа одинаково в соответствии с законом поместного значения цифр.

Устная нумерация:

В числе 13 называются сначала единицы, затем десятки.

В числе 31 называются сначала десятки, потом единицы.

Нумерация от 11 до 20

Устная нумерация двузначных чисел строится на использовании первых девяти чисел натурального ряда от 1 до 9. Существует особенность в названии числа десять, которое обозначает десяток, – «дцать».Устная нумерация начинается с формирования понятия о десятке как о новой счетной единице.

Образование чисел второго десятка

Полезно показать детям практически (полоски, брусок, палочки).

Говорим, что две единицы и один десяток.

Во время устной нумерации включаем упражнения на освоение натуральной последовательности, а именно счет.

При изучении письменной нумерации обучающиеся овладевают умением записывать числа, определять, на каком месте пишутся десятки, единицы, как обозначать отсутствующие разряды единиц. Вводятся понятия однозначного и двузначного числа.

Нумерация от 21 до 100

Устная нумерация

Главная задача – сформировать умение у детей называть любое двузначное число и находить его место в нумерационном ряду.

Повторяем счет группами и по одному.

Для счета десятками полезно использовать наглядные пособия (полоски, бруски, палочки, пуговицы, счеты). Например, палочки связываем пучками.

Письменная нумерация

На этом отрезке чисел вводится термин «разряд»– разъясняется, что такое единицы первого и второго разрядов.

Обязательно организуем работу по усвоению десятичного состава числа и натуральной последовательности.

Используем упражнения на осознание детьми позиционной записи:

– Чем интересны числа 5, 6, 55, 65, 56, 66?

– Что обозначает каждая цифра в этих числах?

Рассматриваются случаи сложения и вычитания вида 20 + 4, 24 – 4, 24 – 20.

Содержание изучаемого учащимися материала в концентре «Тысяча».

Нумерация чисел в пределах 1000 и арифметические действия над ними выделяются в особый концентр по следующим причинам:

1) здесь заканчивается изучение нумерации чисел первого класса – класса единиц, что является основой для изучения нумерации многозначных чисел, т.к. следующие классы (класс тысяч, миллионов и т.д.) строятся по аналогии.

2)закрепляются знания устных приемов вычислении, которые раскрываются с опорой на теорию арифметических действий

3) в этом концентре начинается работа над письменными приемами сложения и вычитания

4) тема «Тысячи» изучается во 2 полугодии 2 класса. Материал рассматривается в таком порядке: нумерация, сложение и вычитание (устные, а затем письменные приемы), умножение и деление (устные приемы вычислений).одновременно ведется работа над составными задачами, продолжается работа над числовыми и буквенными выражениями, над равенствами и неравенствами, уравнениями, а также над геометрическим материалом (закрепляются умения измерять и вычислять периметр фигур, чертить круг и назвать его элементы).

Особенностью изучения нумерации чисел в концентре «Тысяча» является использование аналогии как основного метода, а в качестве часто используемого приёма – анализ готового выражения. Это объясняется тем, что учащиеся уже знакомы с основными вопросами, изучаемые в концентрах «Десяток», «Сотня», выполняли соответствующие упражнения, а потому, смогут распространить свои умения на более широкий класс чисел.

В раздел, связанный с освоением нумерации трехзначных чисел, входит: изучение последовательности чисел в пределах 1000, их чтение и запись; знакомство с разрядом сотен, сотней как новой разрядной единицей; представление трехзначного числа в виде суммы разрядных слагаемых.

В целом методика изучения этой темы сходна с изучением нумерации двузначных чисел.

Для того, чтобы записать число 352, сначала построим его модель в верхнем ряду абака. При изучении нумерации следует обратить внимание на формирование умения заменять любое трехзначное число суммой разрядных слагаемых:

583 = 500 + 80 + 3; 405 = 400 + 5; 620 = 600 + 20.

Разрядный состав играет большую подготовительную роль в изучении арифметических действий над трехзначными числами.

Повторение нумерации в пределах 100 позволяет ознакомить детей и с нумерацией в пределах 1000. К этому этапу они уже усвоили образование сотен, от. счета десятками перешли к счету сотнями, повторили и обобщили вывод о том, что десятками и сотнями считают так же, как простыми единицами. Уже на первом уроке дети узнали названия чисел, которые образуются при счете сотен. На основе знания состава двузначных чисел из десятков и единиц дети легко перешли к усвоению состава трехзначных чисел (2 д. 3 ед.=23, 1 с. 2 д. 3 ед.= 123). Работа с таблицей разрядов, с индивидуальными счетными книжками помогает учащимся усвоить письменную нумерацию трехзначных чисел и понятие разряда (единицы - единицы I разряда, десятки - единицы II разряда, сотни - единицы Ш разряда).

Содержание изучаемого учащимися материала в концентре «Многозначные числа».

Нумерация многозначных чисел и действия над ними выделяются в особый концентр по следующим причинам:

- многозначные числа образуются, называются, записываются с опорой и на понятие разряда, и на понятие класса;

- арифметические действия, в основном, выполняются с использованием письменных вычислений.

В результате изучения нумерации многозначных чисел учащиеся должны:

- усвоить названия и последовательность чисел натурального ряда в пределах класса миллионов, понять, как они образуются, знать их десятичный состав;

- знать названия классов (класс единиц, класс тысяч, класс миллионов) и разрядов внутри каждого класса (единицы, десятки, сотни, единицы тысяч, десятки тысяч и т.д.);

- научиться читать и записывать любое число в пределах класса миллионов, представлять любое число в виде суммы его разрядных слагаемых;

- уметь переносить все приемы работы над числами, изученными в предыдущих концентрах, в данный концентр.

Изучение нумерации многозначных чисел начинают с повторения нумерации чисел в пределах 1000. Повторяются все виды упражнений по общей схеме разбора числа, повторяется работа с нумерационной таблицей, все термины, относящиеся к нумерации. Наиболее удобным наглядным пособием для изучения многозначных чисел являются русские счеты, но, к сожалению, они исчезли. Как демонстрационный материал учитель может использовать пособие, сделанное из миллиметровой бумаги, где 1 полоска со сторонами 10 мм и 100 мм показывает 1000 (единицы - 1 мм²). Однако, ими единицы практически трудно показать, но для изучения чисел с более высокими разрядами они незаменимы. 10 таких полосок изображают число 10000.

После ознакомления с числами 10000, 100000, учащиеся знакомятся с классами: 1 класс - класс единиц, 2 класс - класс тысяч (читают по учебнику). Затем сравнивают 1 и 2 классы и устанавливают их сходство и различие: в каждом классе по три разряда, единицы каждого разряда в 10 раз больше предыдущей, но в 1 классе считают и группируют единицы, а в 2 классе - тысячи.

Далее изучаются числа 2 класса - числа вида 75000, 600000, 392000. Работа, в основном, ведется по нумерационной таблице. Выставляя соответствующие цифры учитель обращает внимание на особенности записи чисел 2 класса: три нуля в конце обозначают отсутствие единиц 1, 2, 3 разрядов, т.е. отсутствие единиц 1 класса, но не отсутствие самих разрядов или класса. Рассматривая десятичный состав чисел 2 класса, учащиеся говорят: 392000 - это 3 сотни тысяч, 9 десятков тысяч и 2

единиц тысяч. Повторяют также другие упражнения по общей схеме разбора числа.

На следующем этапе изучаются числа, состоящие из единиц первого и второго класса. Первые упражнения проводятся по нумерационной таблице, куда выставляются карточки с цифрами.

В дальнейшем при разборе числа ограничиваются названием разрядов: 923427 - это 923427 единиц; 92342 десятка; 9234 сотни; 923 тысячи; 92 десятки тысяч; 9 сотен тысяч.

Работа по изучению нумерации завершается отработкой навыков применения общей схемы разбора числа.

Изучение нумерации многозначных чисел завершается с ознакомление учащихся классами миллиардов и триллионов.

Отметим, что наиболее ответственной при изучении нумерации является усвоение терминологии. Это нужно в будущем для правильного объяснения письменных вычислений и, особенно важно в связи с изучением десятичных дробей в 5 классе.

Закрепление.

- анализ решенных примеров.

- решение примеров с подробными, затем краткими объяснениями,

- самостоятельное решение примеров,

- объяснение ошибок, допущенных в решение

Ознакомление с долями.

Ознакомить детей с долями - значит сформировать у них конкретные представления о долях, то есть научить детей образовывать доли практически. Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть

Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги;

Познакомить детей с долями можно таким образом. У каждого из учащихся и у учителя по несколько одинаковых кругов, прямоугольников. Учитель: «Возьмите два одинаковых круга. Один из них разделите на две равные части (показывает, как надо перегнуть и как разрезать круг). Это целый круг, а это половина круга, иначе говоря, одна вторая доля круга. Сколько вторых долей в целом круге? (2) . Покажите их.

Доли записывают с помощью двух чисел. Одна вторая доля круга, квадрата обозначается так: 1/2. Число 2 показывает, что круг, квадрат или другая фигура (предмет), разделена на 2 равные части, а число 1 показывает, что взяли одну такую часть.

Так же образуются доли 1/4, 1/8, 1/3, 1/6, 1/5, 1/10 и др. При этом учащиеся должны уяснить, что для получения например, 1/5 отрезка (прямоугольника, бумажной полоски) надо данный отрезок (прямоугольник , полоску) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке 5 пятых долей, что одна пятая доля записывается так: 1/5, что в этой записи число 5 обозначает, на сколько равных частей разделен отрезок, а число 1, - что взята одна такая часть. Для закрепления этих знаний и умений учащимся предлагают различные упражнения.

Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. В этом их основное назначение.

В 3 классе рассматривается только простые задачи, а в 4 классе они включаются в составные.

Ознакомление с дробями.

Образование дробей, как и образование долей рассматривается с помощью наглядных пособий.

Ознакомление начинается с упражнений вида: «Разделите круг на 4 равные части. Как назвать каждую такую часть? Запишите. Покажите три четвертые доли. Вы получили дробь - три четвертых. Кто сможет записать эту дробь? Что показывает число 4 (на сколько равных частей разделили круг)? Что показывает число 3 (сколько таких частей взяли)?

Конкретный смысл дроби очень ярко раскрывается при решении задач на нахождение доли числа («В классе 32 ученика. Из них 1/4 играют в хоккей. Сколько хоккеистов в классе?»)

В дальнейшем, решая такие задачи, учащиеся должны самостоя-тельно выполнять подобные рассуждения. Например, надо узнать, сколько минут в 3/4 ч. Ученик рассуждает: «Найду, сколько минут составляет 1/4 ч, для этого 60 разделю на 4, получится 15; теперь найду, сколько минут в 3/4 ч, для этого 15 умножу на 3, получится 45; значит, 3/4 ч -- это 45 мин».

Помним, что чем больше долей, тем меньше каждая доля.

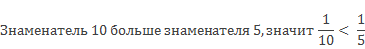
вывод: из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше

Пример простой задачи

По содержанию.

Экологические;
Астрономические;
Географические и т.д.

Цель :

-создать условия для самовыражения, самореализации каждого ученика и для развития самостоятельной деятельности.

- Развитие инициативности и активности обучающихся;

- Развитие навыков проектно-исследовательской работы, умения самостоятельно и творчески мыслить, использовать полученные знания на практике;

- Развитие у обучающихся самостоятельной познавательной деятельности

-Поддержание тесного контакта с родителями, взаимодействие с ними в плане организации совместной деятельности и расширения кругозора учащихся в области научных достижений.

ЗАДАЧИ:

В ходе проектной деятельности формируются способности: Рефлексировать; Целеполагать; Планировать; Проявлять инициативу при реализации идеи проекта, при поиске способа решения проблемы; Вступать в коммуникацию.

Проектная деятельность окружающего мира проходит в несколько этапов.

Первый этап - организационный

Второй этап - целеполагание

Третий этап – подготовительный

Четвертый этап – выполнение проекта

Пятый этап – практическое применение разработанного проекта

Шестой этап – самоанализ

Седьмой этап – подведение итогов

Действия родителей могут быть такими:

-проявлять заинтересованность (важный фактор поддержания мотивации);

-помочь советом, информацией (источник информации может быть опрос, наблюдение, эксперимент, интервью, а также книги и периодические издания, Интернет);

-обеспечение самостоятельности школьников;

-активное участие на каждом этапе проектной деятельности.

ОТВЕТЫ

«МЕТОДИКА ПРЕПОДАВАНИЯ ПРЕДМЕТНЫХ ОБЛАСТЕЙ «МАТЕМАТИКА», «ОКРУЖАЮЩИЙ МИР»

Методика обучения математике как науке. Предмет и задачи, связь с другими науками.

Методика обучения математике — это педагогическая наука о задачах, содержании и методах обучения математике. Она изучает и исследует процесс обучения математике в целях повышения его эффективности и качества. Методика обучения математике рассматривает вопрос о том, как надо преподавать математику;

Для решения проблем методического характера используют следующие методы: эксперимент; изучение и использование отечественного и зарубежного опыта обучения учащихся; анкетирование, беседы с учителями и учащимися; анализ; синтез, моделирование, ранжирование, шкалирование и т.д.

Для доказательства предполагаемых суждений в методике обучения математике используют эксперимент — организуемое обучение с целью проверки гипотезы, фиксации реального уровня знаний, умений, навыков, развития ученика, сравнения результативности предлагаемых методик и традиционно используемых, обоснования различных утверждений. В организации эксперимента используются: наблюдение, анкетирование, качественный и количественный анализ результатов обучения.

Качественный анализ результатов исследования осуществляется с помощью контрольных работ, тестирования школьников, а количественный — по результатам статистической обработки контрольных работ, тестов.

Учебный предмет математики в школе представляет собой элементы арифметики, алгебры, начал математического анализа, евклидовой геометрии плоскости и пространства, аналитической геометрии, тригонометрии.

Цель методики обучения математике заключается в исследовании основных компонентов системы обучения математике в школе и связей между ними. Под основными компонентами понимают цели, содержание, методы, формы и средства обучения математике.

Основными задачами методики преподавания математики являются:

- определение конкретных целей изучения математики по классам, темам, урокам;

- отбор содержания учебного предмета в соответствии с целями и познавательными возможностями учащихся;

- разработка наиболее рациональных методов и организационных форм обучения, направленных на достижение поставленных целей;

- выбор необходимых средств обучения и разработка методики их применения в практике работы учителя математики.

Методика преподавания математики призвана дать ответы на три вопроса: Зачем надо учить математике? Что надо изучать? Как надо обучать математике?

Методика обучения математике связана с такими науками, как философия, психология, педагогика, логика, информатика, история математики и математического образования, физиология человека, и прежде всего с математикой — ее базовой дисциплиной.

2. Начальный курс обучения математике как учебный предмет. Цели и содержание обучения математике в начальных классах.

Обучение математике, так же как и обучение любому другому предмету в школе, должно решать образовательные, воспитательные, развивающие и практические задачи.

Математическое образование – это сложный процесс, основными компонентами которого являются приобретение учащимися определенной системы математических фактов и знаний, овладение определенными математическими умениями и навыками, развитие математического мышления.

Изучение математики способствует формированию научного мировоззрения учащихся, воспитанию трудолюбия, дисциплинированности и других важных моральных качеств.

При изучении математики дети учатся видеть связь математики с реальным миром, который окружает ребенка, и с его жизнью. С одной стороны, надо учить детей распознавать в явлениях окружающего мира математические факты. С другой стороны, надо учить применять математические знания в повседневной жизни.

Цели обучения в курсе математики в 1–4 классах, сформулированные как линии развития личности ученика средствами предмета: