Задачи для решения
Вычислить тепловой эффект и изменение энергии Гиббса при 298 K для реакции в водном растворе
Реакции надо уравнять (окислительно-восстановительные реакции надо опознать и применить метод полу-реакций).
| № | Схема реакции |
| 1. | Al2(SO4)3 (aq) + BaCl2 (aq) = AlCl3 (aq) + BaSO4 (тв.) |
| 2. | Br2 (aq) + KCrO2 (aq) + KOH (aq) = KBr (aq) + K2CrO4 (aq) + H2O (ж) для Br2 (aq): Δf Нo298 = -2,59 кДж/моль; Δf Go298 = -41,48 кДж/моль для CrO2-(aq): Δf Нo298 = -620,5 кДж/моль; Δf Go298 = -612,10 кДж/моль |
| 3. | C (графит) + K2Cr2O7 (aq) + H2SO4 (aq) = CO2 (г) + Cr2(SO4)3 (aq) + K2SO4 (aq) + H2O (ж) |
| 4. | Ca3(PO4)2 (тв.) + H2SO4 (aq) = CaSO4 (тв.) + H3PO4 (aq) при 25°С для H3PO4 (aq): Δf Нo298 = -1277,5 кДж/моль; Δf Go298 = -1143,0 кДж/моль |
| 5. | CaCl2 (aq) + Na2CO3 (aq) = CaCO3 (тв.) + 2NaCl (aq) |
| 6. | Cd (тв.) + CuSO4 (aq) = CdSO4 (aq) + Cu (тв.) |
| 7. | CuO (тв) + NH4OH (aq) = [Cu(NH3)4](OH)2 (aq) + H2O (ж) для NH4OH (aq): Δf Ho298 = -362,5 кДж/моль; Δf Go298 = -263,0 кДж/моль |
| 8. | Fe2(SO4)3 (aq) + MnO2 (тв) + H2O (ж) = FeSO4 (aq) + HMnO4 (aq) + H2SO4 (aq) |
| 9. | Hg (ж) + HNO3 (aq) = Hg(NO3)2 (aq) + NO(г) + H2O (ж) |
| 10. | Hg2Cl2 (тв) + KNO3 (aq) = Hg2(NO3)2 (aq) + KCl (aq) |
| 11. | HI (aq) + K2Cr2O7 (aq) + H2SO4 (aq) = I2 (aq) + Cr2(SO4)3 (aq) + K2SO4 (aq) + H2O (ж) для I2 (aq): Δf Ho298 = 22,6 кДж/моль; Δf Go298 = 16,0 кДж/моль |
| 12. | I2 (г) + H2O (ж) + Na2SO3 (aq) = 2HI (aq) + Na2SO4 (aq) |
| 13. | K2Cr2O7 (aq) + FeSO4 (aq) + H2SO4 (aq) = Fe2(SO4)3 (aq) + Cr2(SO4)3 (aq) + K2SO4 (aq) + H2O (ж) |
| 14. | K2CrO4 (aq) + KI (aq) + H2O (ж) = I2 (aq) + KCrO2 (aq) + KOH(aq) для CrO2- (aq): Δf Ho298 = -620,5 кДж/моль; ΔfGo298 = -612,1 кДж/моль для I2 (aq): Δf Ho298 = 22,6 кДж/моль; Δf Go298 = 16 кДж/моль |
| 15. | KI (aq) + K2Cr2O7 (aq) + H2SO4 (aq) = KIO3 (aq) + Cr2(SO4)3 (aq) + K2SO4 (aq) + H2O (ж) |
| 16. | KMnO4 (aq) + FeSO4 (aq) + H2SO4 (aq) = MnSO4 (aq) + Fe2(SO4)3 (aq) + K2SO4 (aq) + H2O(ж). |
| 17. | KMnO4 (aq) + MnSO4 (aq) + H2O(ж) = MnO2 (тв) + K2SO4 (aq) + H2SO4 (aq) |
| 18. | KMnO4 (aq) + Na2SO3 (aq) + H2O (ж) = MnO2 (тв) + KOH (aq) + Na2SO4 (aq) |
| 19. | KMnO4 (aq) + Na2SO3 (aq) + H2SO4 (aq) = MnSO4 (aq) + K2SO4 (aq) + Na2SO4 (aq) + H2O(aq) |
| 20. | KMnO4 (aq) + NaBr (aq) + H2SO4 (aq) = NaBrO3 (aq) + K2SO4 (aq) + MnSO4 (aq) + H2O (ж) |
| 21. | KMnO4 (aq) + NaNO2 (aq) + KOH(aq) = K2MnO4 (aq) + NaNO3 (aq) + H2O (ж); для MnO42-(aq): ΔfHo298 = -655,2 кДж/моль; ΔfGo298 = -449 кДж/моль |
| 22. | KMnO4 (aq) + NaNO2 (aq) + H2SO4 (aq) = MnSO4 (aq) + K2SO4 (aq) + NaNO3 (aq) + H2O (ж) |
| 23. | KMnO4(aq) + HCl(aq) = KCl(aq) + MnCl2(aq) + H2O(ж) + Cl2(г) |
| 24. | KMnO4 (aq) + H2O2 (aq) + H2SO4 (aq) = MnSO4 (aq) + K2SO4 (aq) + O2 (г); для H2O2 (aq): Δf Ho298 = -191,2 кДж/моль; ΔfGo298 = -134,0 кДж/моль |
| 25. | KMnO4 (aq) + KI (aq) + H2SO4 (aq) = MnSO4 (aq) + I2 (aq) + K2SO4 (aq) + H2O (ж); для I2 (aq): Δf Ho298 = 22,6 кДж/моль; Δf Go298 = 16 кДж/моль |
| 26. | KMnO4 (aq) + KNO2 (aq) + H2O (ж) = MnO2 (тв.) + KNO3 (aq) + KOH (aq) |
| 27. | MnO2 (тв) + NaHSO4 (aq) = NaMnO4 (aq) + NaHSO3 (aq) + H2O (ж) + SO2 (г). |
| 28. | KMnO4 + Na2SO3 + KOH = K2MnO4 + Na2SO4 + H2O для MnO42-(aq): Δf Ho298 = -655,20 кДж/моль; Δf Go298 = -449,00 кДж/моль |
| 29. | Na3AlF6 (тв., α) + NaOH (aq) = NaAlO2 (тв) + NaF (aq) + 2H2O (ж) для NaAlO2 (тв) Δf Ho298 = -1133,03 кДж/моль; Δf Go298 = -1070,00 кДж/моль |
| 30. | Pt (тв) + HNO3 (aq) + HCl (aq) = H2[PtCl6] (aq) + NO (г) + H2O (ж) |
Вычислить энергию Гиббса реакции при заданной температуре
| № | Уравнение реакции | Т, °С |
| 31. | 2CO (г) + SO2 (г) = S2 (г) + 2CO2 (г) | 850 |
| 32. | 2NaHCO3 (тв.) = Na2CO3 (тв.) + H2O (г) + CO2 (г) | 900 |
| 33. | 2NO2 (г) + О3 (г) = О2 (г) + N2O5 (г) | 800 |
| 34. | 4H2S (г) + 2SO2 (г) = 3S2 (г) + 4H2O (г) | 850 |
| 35. | 4HCl (г) + O2(г) = 2H2O(г) + 2Cl2(г) | 700 |
| 36. | 4СО (г) + 2SO2 (г) = S2 (г) + 4CO2 (г) | 850 |
| 37. | CH4 (г) + 2H2S (г) = CS2 (г) + 4H2 (г) | 850 |
| 38. | CH4 (г) + 2O2 (г) = CO2 (г) + 2H2O (г) | 850 |
| 39. | CH4 (г) + СO2 (г) = 2CO (г) + 2H2 (г) | 850 |
| 40. | CuS (тв) + O2 (г) = Cu (т) + SO2 (г) | 800 |
| 41. | CuSO4 (тв) = CuO (тв) + SO3 (г) | 1000 |
| 42. | СuСО3 (тв) = CuO (тв) + СО2 (г); для CuCO3 (тв): ΔfHo298 = -596 кДж/моль, So298 = 88 Дж/(моль·K), а = 92 Дж/(моль·K), b = 39·10-3 Дж/(моль·K), c’ = -18·105 Дж/(моль·K) | 1000 |
| 43. | Fe2O3 (тв) + 3CO (г) = 2Fe (α) + 3CO2 (г) | 700 |
| 44. | Fe2O3 (тв) + C(графит) = Fe (α) + CO2 (г) | 1500 |
| 45. | MgСO3 (т) = MgO (т) + СO2 (г) | 800 |
| 46. | Na2SO4 (α) + 2C(графит) = Na2S (тв) + 2CO2 (г) | 800 |
| 47. | PbCO3 (тв) + H2S (г) = PbS (тв) + H2O (г) + CO2 (г). | 500 |
| 48. | SiO2(кварц-α) + 4HF(г) = SiF4 (г) + 2H2O (г) | 800 |
| 49. | CaCO3 (кальцит) = CaO (тв) + CO2 (г) | 800 |
| 50. | Al2O3 (корунд) + Na2CO3 (α) = 2NaAlO2 (тв) + CO2 (г) | 450 |
| 51. | TiO2 (рутил) + CCl4 (г) = TiCl4 (г) + CO2 (г) | 700 |
| 52. | 2Fe(OH)3(тв) = Fе2O3(тв) + 3H2O(г); для Fe(OH)3(тв): ΔfHo298=-823 кДж/моль, So298=-105 Дж/(моль·K), a = 85,51 Дж/(моль·K), b = 123,24·10−3 Дж/(моль·K), c’ = −15,12·105 Дж/(моль·K), | 900 |
| 53. | 2PbS (тв) + 3O2 (г) = 2PbO (тв, желтый) + 2SO2 (г) | 500 |
| 54. | Ni(OH)2 (тв) = NiO (тв) + H2O (г); для Ni(OH)2 (тв): ΔfHo298 = -547,1 кДж/моль, So298 = 88 Дж/(моль·K), а = 88 Дж/(моль·K), b = 93·10-3 Дж/(моль·K), с’ = 13·105 Дж/(моль·K) | 1000 |
| 55. | Cu(OH)2 (тв) = CuO (тв) + H2O (г); для Cu(OH)2 (тв): ΔfHo298 = -443,09 кДж/моль, So298 =81 Дж/(моль·K), а = 87 Дж/(моль·K), b = 23,3·10-3 Дж/(моль·K), с’ = -5,4·105 Дж/(моль·K) | 1000 |
| 56. | 4CuS (тв) = 2Cu2S (тв) + S2 (г) | 1200 |
| 57. | Cu2O (тв) + FeS (α) = Cu2S (тв) + FeO (тв) | 1200 |
| 58. | 6FeO (тв) + 4O2 (г) = 2Fe3O4 (тв) | 1400 |
| 59. | 3CaSO4 (тв) + CaS (тв) = 4CaO (тв) + 4SO2 (г) | 1000 |
| 60. | CaSO4 (тв) + 4CO (г) = CaS (тв) + 4CO2 (г) | 1000 |
Метод Темкина-Шварцмана
Пример 5. Вычислить энергию Гиббса реакции 4NH3 (г) + 5O2 (г) = 6H2O (г) + 4NO (г) при 850 K.
Решение. 1. Составить таблицу справочных данных, необходимых для расчета:
| Компонент | NH3 (г) | O2 (г) | H2O (г) | NO (г) |
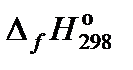 , кДж/моль , кДж/моль
| −45,94 | 0 | −241,81 | 91,26 |
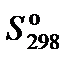 , Дж·моль−1·K−1 , Дж·моль−1·K−1
| 192,66 | 205,04 | 188,72 | 210,64 |
| a, Дж·моль−1·K−1 | 29,80 | 31,46 | 30,00 | 29,58 |
| b·103, Дж·моль−1·K−1 | 25,48 | 3,39 | 10,71 | 3,85 |
| c’·10−5, Дж·моль−1·K−1 | −1,67 | −3,77 | 0,33 | −0,59 |
2. Составить уравнение для расчета теплового эффекта реакции при 298 K и произвести необходимые вычисления:
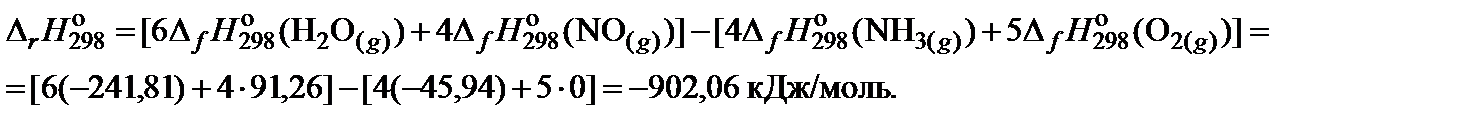
3. Составить уравнение для расчета изменения энтропии реакции в соответствии с законом Гесса и произвести необходимые вычисления:
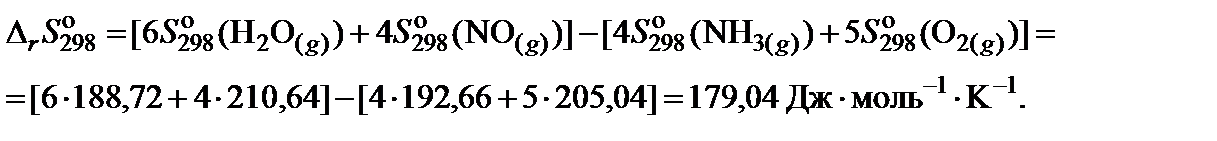
4. Пользуясь законом Гесса, найти изменение коэффициентов теплоемкости в ходе процесса:
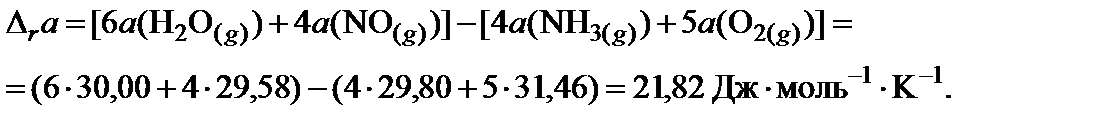
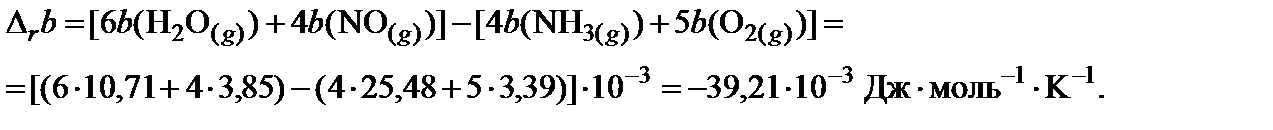
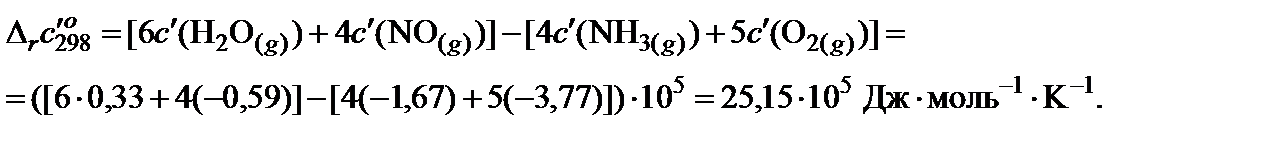
5. В таблице 45 краткого справочника физико-химических величин находят значения интегралов М0, М1 и М‒2 при температуре 800 K и 900 K. Величины для 850 K находят как среднее арифметическое для значений температуры 800 и 900 K.
| T, K | M0 | M1∙10‒3 | M2∙10‒6 | M‒2∙105 |
| 800 | 0,3597 | 0,1574 | 0,0733 | 0,2213 |
| 900 | 0,4361 | 0,2012 | 0,1004 | 0,2521 |
| 850 | 0,3979 | 0,1793 | 0,2376 |
6. Подставить данные в расчетную формулу:
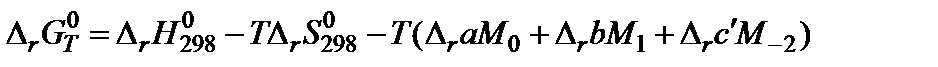 :
:
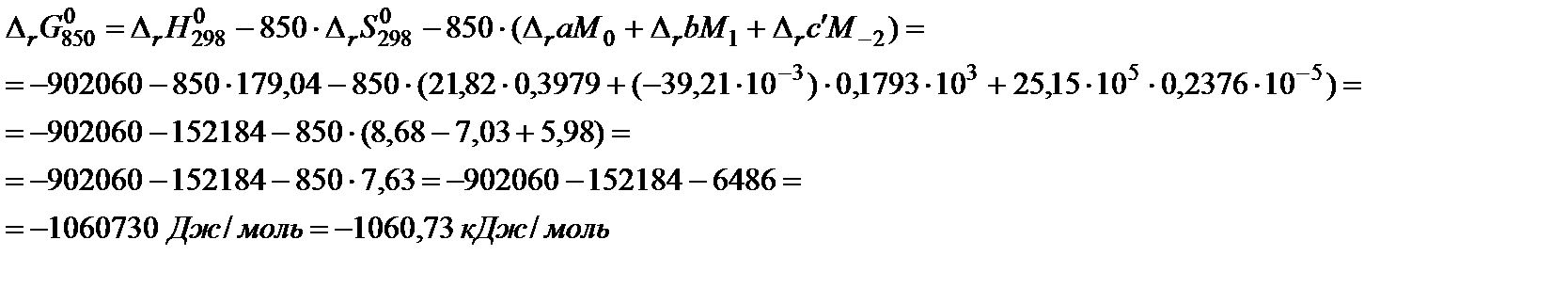
7. Вычислить константу равновесия по формуле:
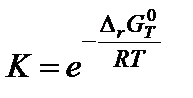 ;
; 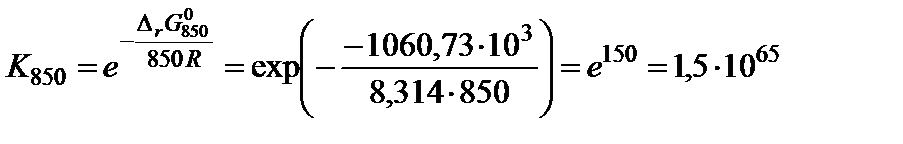
Задачи для решения
2.1. Вычислить константу равновесия реакции, протекающей в водном растворе при 25°С и заданной температуре.
| № | Вещество | Процесс | Т, °С | 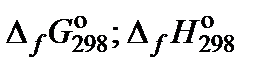 , кДж/моль , кДж/моль
|
| 61. | (СН3СOO)2Ba | гидролиз | 60 | 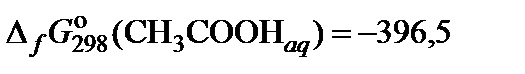
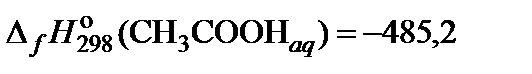
|
| 62. | Ag2CO3 | растворимость | 80 | См. краткий справочник |
| 63. | NH4NO3 | гидролиз | 80 | 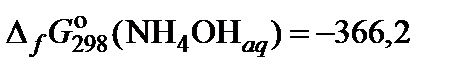
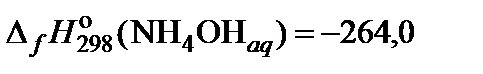
|
| 64. | Hg2CrO4 | растворимость | 90 | См. краткий справочник |
| 65. | Na3PO4 | гидролиз | 70 | См. краткий справочник |
| 66. | CaCO3 | растворимость | 60 | См. краткий справочник |
| 67. | Na2HPO3 | гидролиз | 90 | См. краткий справочник |
| 68. | CaSO4 | растворимость | 70 | См. краткий справочник |
| 69. | FeCl3 | гидролиз | 60 | 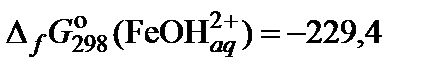
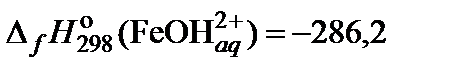
|
| 70. | PbCl2 | растворимость | 80 | 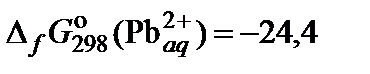
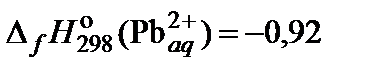
|
| 71. | MnCl2 | гидролиз | 70 | 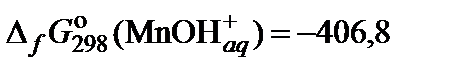
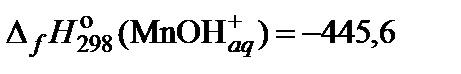
|
| 72. | Li3PO4 | растворимость | 90 | См. краткий справочник |
| 73. | Sn(NO3)2 | гидролиз | 80 | 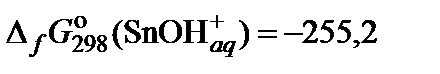
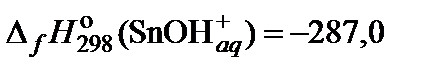
|
| 74. | PbI2 | растворимость | 80 | 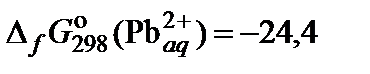
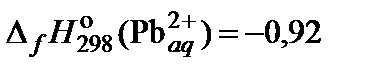
|
| 75. | Zn(NO3)2 | гидролиз | 70 | 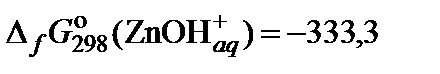
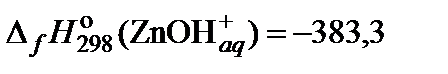
|
| 76. | HCOOK | гидролиз | 90 | 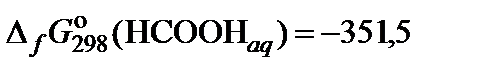
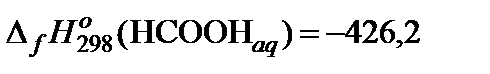
|
| 77. | K2C2O4 | гидролиз | 60 | См. краткий справочник |
| 78. | Са3(РО4)2 | растворимость | 60 | См. краткий справочник |
| 79. | Na2CO3 | гидролиз | 80 | |
| 80. | AgCN | растворимость | 80 | См. краткий справочник |
| 81. | KHCO3 | гидролиз | 70 | 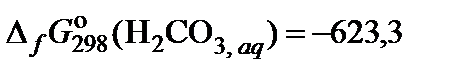
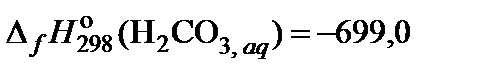
|
| 82. | BaSO3 | растворимость | 60 | См. краткий справочник |
| 83. | Na2S | гидролиз | 90 | См. краткий справочник |
| 84. | Zn(OH)2 | растворимость | 90 | См. краткий справочник |
| 85. | Na2SO3 | гидролиз | 60 | См. краткий справочник |
| 86. | CaC2O4 | растворимость | 70 | См. краткий справочник |
| 87. | NaNO2 | гидролиз | 80 | 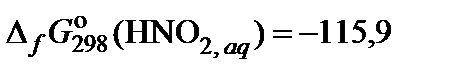
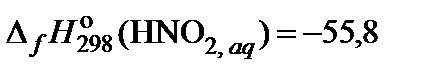
|
| 88. | BaCO3 | растворимость | 90 | См. краткий справочник |
| 89. | MgCO3 | растворимость | 70 | См. краткий справочник |
| 90. | Fe(OH)2 | растворимость | 70 | См. краткий справочник |
Задачи для решения
Общая информация
Неконденсированные системы изучают с помощью как изобарических сечений диаграмм их состояния (в координатах температура и состав), так и изотермических сечений в координатах давление - состав.
В уравнении, определяющем число степеней свободы системы по правилу фаз Гиббса, число внешних переменных уменьшается до единицы
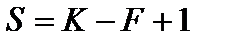 .
.
Максимальное число фаз, находящихся в равновесии в таких системах, не превышает трех, системы с двумя фазами имеют одну степень свободы, а с одной - две степени свободы.
Типовые диаграммы состояния
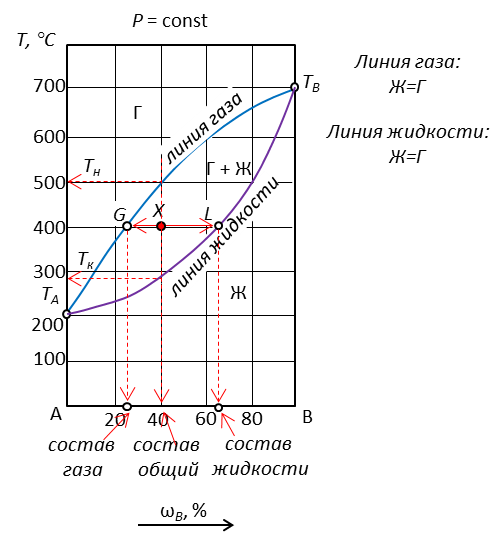
Рис. 1. Диаграмма с неограниченной растворимостью компонентов, без точек азеотропа
Свойства систем, заданных фигуративными точками
| Точка | Исходный состав, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура конденсации | Число степеней свободы | |
| ТН | ТK | |||||||
| X | 40 | 2 | Ж | 65 | 37,5 | 500 | 290 | 2-2+1=1 |
| Г | 25 | 62,5 | ||||||
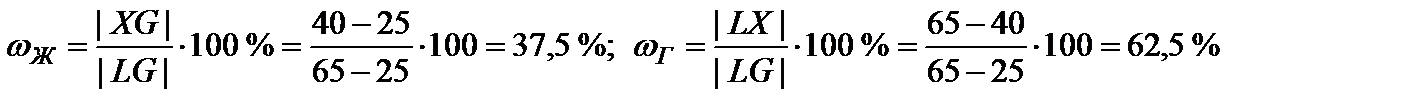
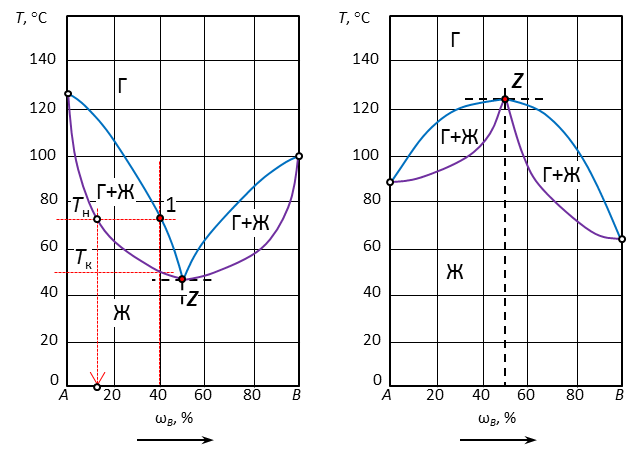
Рис. 2. Диаграмма с неограниченной растворимостью компонентов и нижним азеотропом
| Точка | Исходный состав, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура конденсации | Число степеней свободы | |
| ТН | ТK | |||||||
| 1 | 40 | 2 | Ж | 12 | Ж=Г | 72 | 50 | 2-2+1=1 |
| Г | 40 | |||||||
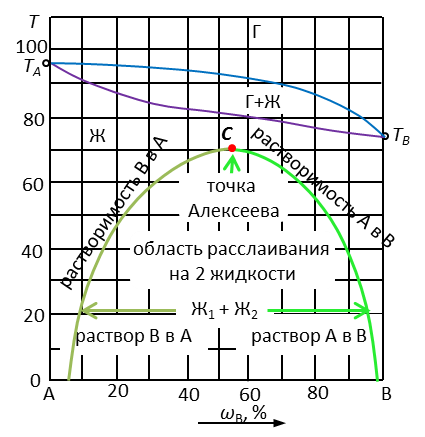
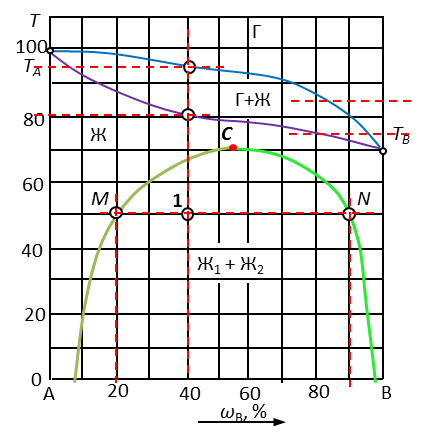
Рис. 3. Диаграмма с областями полной и частичной растворимостью жидкостей
| Точка | Исходный состав системы, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура конденсации | Число степеней свободы F=K-Ф+1 | |
| ТН | ТK | |||||||
| 1 | 40 | 2 | ж1 | 20 | 75 | 95 | 80 | 2-2+1=1 |
| ж2 | 90 | 25 | ||||||
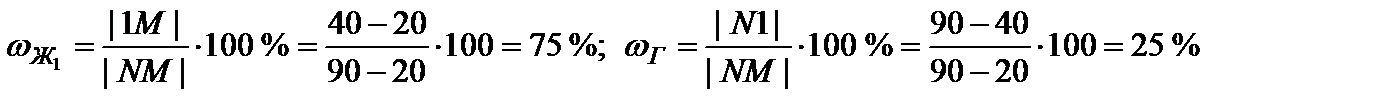
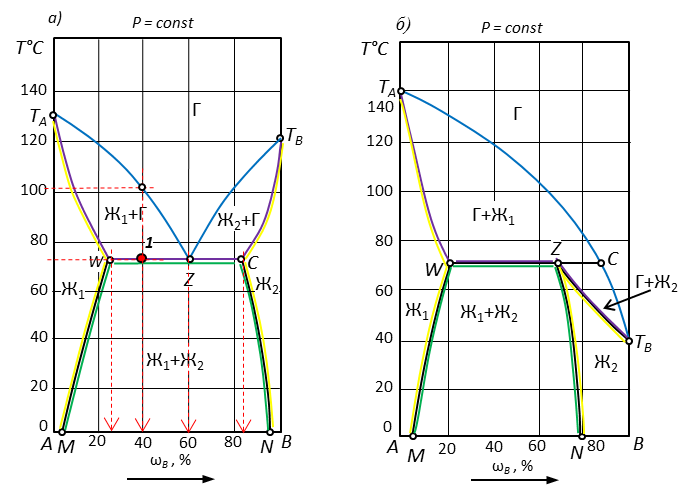
Рис. 4. Диаграмма с ограниченной растворимостью компонентов, полной растворимости нет.
| Точка | Исходный состав системы, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура конденсации | Число степеней свободы F=K-Ф+1 | |
| ТН | ТK | |||||||
| 1 | 40 | 3 | Ж1 | 25 | Ж1=Ж2=Г | 101 | 72 | 2-3+1=0 |
| Г | 60 | |||||||
| Ж2 | 82 | |||||||
Порядок рассмотрения диаграммы
1. Перечертить диаграмму, соблюдая топологию, в заданном масштабе.
2. Дать общую характеристику диаграммы.
3. Отметить линию газа, линию жидкости, линии растворимости компонентов; написать равновесия на линиях.
4. Обозначить поля диаграммы греческими или римскими цифрами.
5. Указать фазовый состав полей диаграммы.
6. Описать значимые точки диаграммы (точки кипения компонентов, точки азеотропа, точки Алексеева): указать температуру, состав, уравнение равновесия.
7. Рассмотреть свойства систем, заданных соответствующими фигуративными точками и заполнить таблицу
| Точка | Исходный состав, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура конденсации | Число степеней свободы | |
| ТН | ТK | |||||||
Примеры решения задач
Пример 9. Обозначить поля диаграммы (рис. 5), дать характеристику компонентов системы. Описать путь конденсации системы, содержащей 45 % компонента В (точка М), заполнить таблицу.

Рис. 5. Диаграмма состояния двухкомпонентной неконденсированной системы пентан – гептан.
Решение. 1. Пронумеровать поля диаграммы (обычно – римскими цифрами).
2. Дать наименование полей диаграммы. Поле I – газ (пар); поле II – пар + жидкость; поле III – жидкость.
3. Дать характеристику диаграммы. Двухкомпонентная неконденсированная система с неограниченной растворимостью компонентов в жидкой фазе.
4. Путь конденсации системы – вертикальная пунктирная линия вниз от точки М (рис. 6), на которой отмечены фигуративные точки М', М'', М''', соответствующие началу процесса (М'), образованию двухфазной системы (М'') и окончанию конденсации (М''').
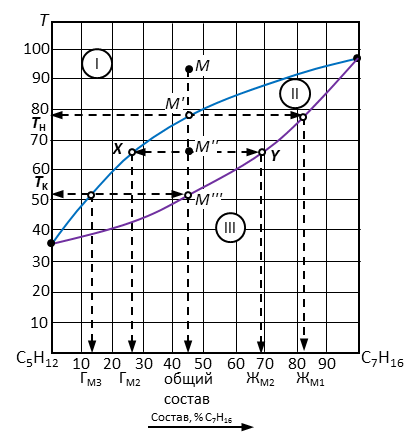
Рис. 6. Решение примера 1.
5. Таблица
| Точка | Исходный состав системы, % В | Кол-во фаз в точке | Наим. фаз | Состав каждой фазы, % В | Относит. кол-во фаз, % | Температура конденсации | C | |
| ТН | ТK | |||||||
| М | 45 | 1 | Г | 45 | 100 | 78 | 51 | 2 |
| М' | 45 | 2 | Г | 45 | Г=Ж | 78 | 51 | 1 |
| Ж | 82 | |||||||
| М'' | 45 | 2 | Г | 27 | 55 | 78 | 51 | 1 |
| Ж | 69 | 45 | ||||||
| М''' | 45 | 2 | Г | 13 | Г=Ж | 78 | 51 | 1 |
| Ж | 45 | |||||||
5. Определить состав системы в точке М, для чего следует опустить перпендикуляр от точки М на ось составов. Состав точки М – 45 % гептана C7H16 – компонента В. Он же будет общим составом системы для всех остальных точек. Точка М находится в поле I, следовательно, число фаз – 1 шт. Наименование фазы – пар; состав совпадает с общим составом системы.
6. Температуру начала конденсации определить по месту пересечения перпендикуляра из точки М и линии газа (граничной линии между полем I и II) – точка М'. От точки М' провести горизонталь на ось температур. Температура начала конденсации равна 78°С. Она остается одинаковой для всех рассматриваемых точек.
7. Определить число степеней свободы в точке М:
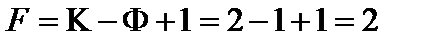 .
.
8. Определить фазовый состав в точке М'. Точка М' находится на линии конденсации, следовательно, количество фаз – 2 шт.: газ и жидкость.
9. Определить состав жидкости в точке М', для чего от этой точки провести ноду до пересечения с линией жидкости (или линией испарения) и от точки пересечения опустить перпендикуляр на ось составов (позиция ЖМ' на рис. 6). Состав жидкости – 82 % C7H16.
10. Определить относительное количество фаз в точке М': так как М' находится на линии равновесия между двумя фазами, то относительное их количество не определяется. В такой ситуации следует записать уравнение равновесия. В данном случае – Ж = Г.
11. Определить число степеней свободы в точке М':
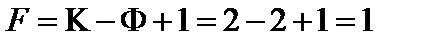 .
.
12. Определить фазовый состав точки М'', которая находится в поле II, следовательно, число фаз – 2 шт.: жидкость и газ.
13. Определить состав жидкости и газа в точке М'': провести ноду до пересечения с линий испарения (точка X) с одной стороны и с линией конденсации (точка Y) с другой стороны. От точек пересечения опустить перпендикуляры на ось составов. Перпендикуляр от линии конденсации определяет состав газа (27 % гептана – точка ГМ'' на рис. 6), от линии испарения – состав жидкой фазы (69 % гептана – точка ЖМ'' на рис. 6).
14. Определить относительное количество фаз в точке М''. В соответствии с правилом рычага
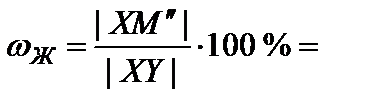 45%;
45%; 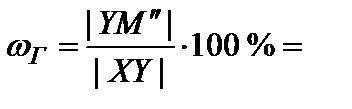 55 %.
55 %.
15. Определить число степеней свободы в точке М'':
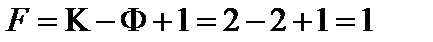 .
.
16. Температуру завершения процесса конденсации определить по месту пересечения перпендикуляра из точки М с линией испарения – точка М'''. От точки М''' провести горизонталь на ось температур. Температура завершения конденсации равна 51°С. Она остается одинаковой для всех рассматриваемых точек.
17. Определить фазовый состав в точке М'''. Точка М''' находится на линии испарения, следовательно, количество фаз – 2 шт.: газ и жидкость.
18. Определить состав пара в точке М''', для этого от этой точки провести ноду до пересечения с линией конденсации и от этой точки опустить перпендикуляр на ось составов (позиция ГМ''' на рис. 6). Состав пара – 13 % C7H16.
19. Определить относительное количество фаз в точке М''': так как М''' находится на линии равновесия между двумя фазами, то относительное их количество не определяется. В такой ситуации следует записать уравнение равновесия. В данном случае – Ж = Г.
20. Определить число степеней свободы в точке М''':
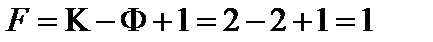 .
.
Пример 10. Обозначить поля диаграммы (рис. 7), дать характеристику компонентов системы. Определить изменение состава и количества фаз в системе, содержащей 25 % анилина при охлаждении ее от 170 до 60°С с интервалом 40°С. Нанести на диаграмму соответствующие фигуративные точки систем и фаз, заполнить таблицу.
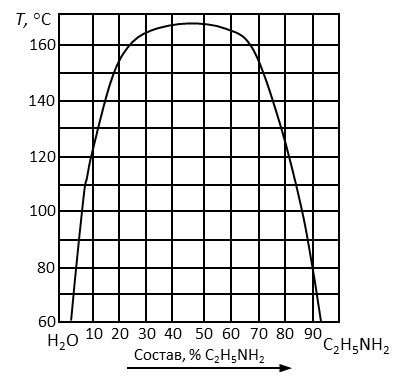
Рис. 7. Диаграмма состояния вода – этаноламин.
Решение. 1. Пронумеровать поля диаграммы (обычно – римскими цифрами).
2. Дать наименование полей диаграммы: поле I – жидкость (пар); поле II – область расслоения двух жидкостей.
3. Дать характеристику диаграммы: двухкомпонентная неконденсированная система с ограниченной растворимостью компонентов в жидкой фазе.
4. Отметить исследуемый состав системы, соответствующий содержанию анилина C2H5NH2 25 % и отметить фигуративные точки N, N', N'', соответствующие заданному температурному интервалу.
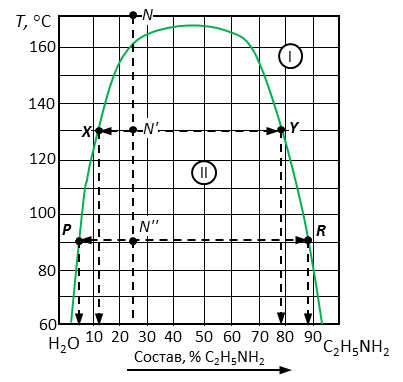
Рис. 8. Решение примера 2.
5. Определить фазовый состав в каждой точке. Точка N принадлежит к полю I, следовательно, количество фаз – 1 шт. – жидкость, содержащая 25 % анилина. Точки N' и N'' принадлежат полю II, где происходит расслаивание системы на две жидкости разного состава, следовательно, количество фаз – 2 шт. Состав жидкостей зависит от температуры.
6. Определить состав расслаивающихся жидкостей в точках N' и N'', как показано на рис. 8 и зафиксировано в табл. 2. При этом следует учитывать, что жидкость 1 представляет насыщенный раствор анилина в воде, а жидкость 2 – раствор воды в анилине. Соответственно точки X и P отображают состав Ж1, а точки Y и R – состав жидкости 2.
7. Пользуясь правилом рычага, определить относительное количество каждой фазы.
Для точки N':
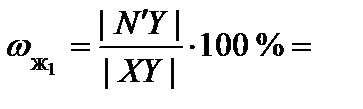 80 %;
80 %; 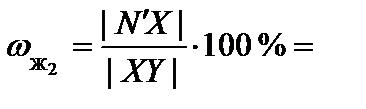 20 %.
20 %.
Для точки N'':
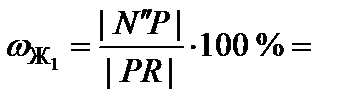 75 %;
75 %; 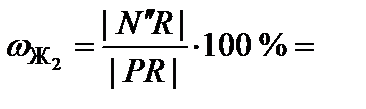 25 %.
25 %.
| Точка | Исходный состав системы, % В | Количество фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное количество фаз, % | |
| N | 25 | 1 | Ж | 25 | 100 | |
| N' | 25 | 2 | Ж1 | 12 | 20 | |
| Ж2 | 78 | 80 | ||||
| N'' | 25 | 2 | Ж1 | 5 | 25 | |
| Ж2 | 88 | 75 |
Задачи для решения
Обозначить поля диаграммы, дать характеристику компонентов системы, заполнить таблицу и т.д. см. пример 9 или пример 10.
181. Описать путь испарения системы с массовой долей CCl4 20 %, рис. 9.
182. Описать путь испарения системы с массовой долей CCl4 40 %, рис. 9.
183. Описать путь испарения системы с массовой долей CCl4 50 %, рис. 9.
184. Описать путь испарения системы с массовой долей CCl4 60 %, рис. 9.
185. Описать путь испарения системы с массовой долей CCl4 80 %, рис. 9
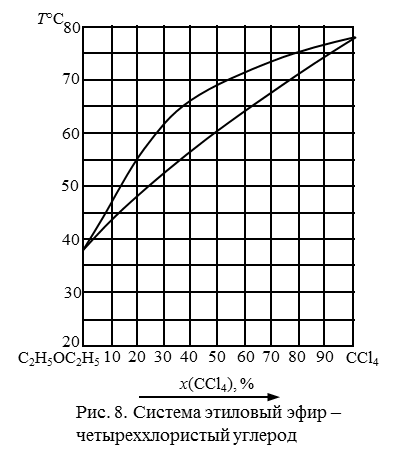
Рис. 9. Система диэтиловый эфир-четыреххлористый углерод.
186. Определить изменение состава и количества фаз в системе, содержащей 15 % воды (рис. 10) при охлаждении от 170 до 60°С с интервалом 40°С.
187. Определить изменение состава и количества фаз в системе, содержащей 25 % воды (рис. 10) при охлаждении от 170 до 60°С с интервалом 40°С.
188. Определить изменение состава и количества фаз в системе, содержащей 35 % воды (рис. 10) при охлаждении от 170 до 60°С с интервалом 40°С.
189. Определить изменение состава и количества фаз в системе, содержащей 45 % воды (рис. 10) при охлаждении от 170 до 60°С с интервалом 40°С.
190. Определить изменение состава и количества фаз в системе, содержащей 55 % воды (рис. 10) при охлаждении от 170 до 60°С с интервалом 40°С.
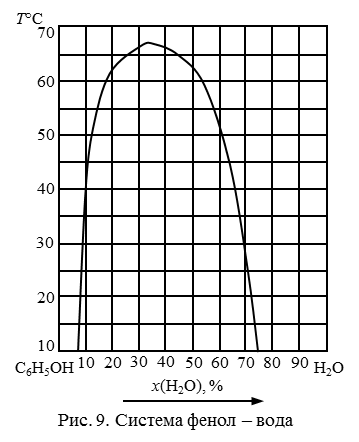
Рис. 10. Система фенол-вода.
191. Описать процессы, происходящие при конденсации системы, содержащей 20 % спирта (рис. 11). Можно ли из раствора заданного исходного состава выделить чистый спирт путем перегонки?
192. Описать процессы, происходящие при конденсации системы, содержащей 40 % спирта (рис. 11). Можно ли из раствора заданного исходного состава выделить чистый спирт путем перегонки?
193. Описать процессы, происходящие при конденсации системы, содержащей 50 % спирта (рис. 11). Можно ли из раствора заданного исходного состава выделить чистый спирт путем перегонки?
194. Описать процессы, происходящие при конденсации системы, содержащей 70 % спирта (рис. 11). Можно ли из раствора заданного исходного состава выделить чистый спирт путем перегонки?
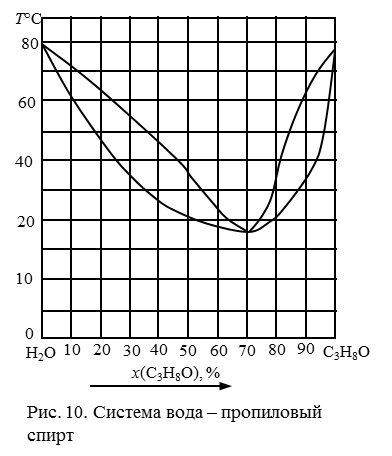
Рис. 11. Система вода – пропанол.
195. Описать процессы, происходящие при испарении раствора, содержащего 30 % кислоты (рис. 12).
196. Описать процессы, происходящие при испарении раствора, содержащего 50 % кислоты (рис. 12).
197. Описать процессы, происходящие при испарении раствора, содержащего 70 % кислоты (рис. 12).
198. Описать процессы, происходящие при испарении раствора, содержащего 10 % уксусной кислоты (рис. 12). Можно ли методом перегонки получить из этого раствора чистую уксусную кислоту?
199. Описать процессы, происходящие при испарении раствора, содержащего 80 % кислоты (рис. 12).
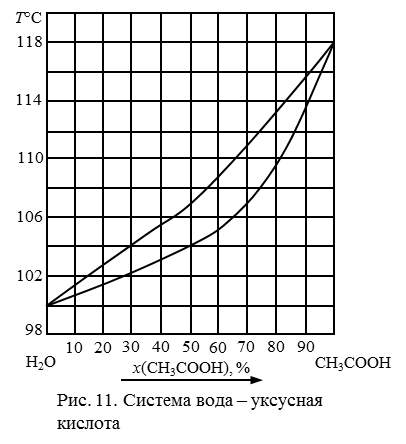
Рис. 12. Диаграмма состояния системы вода – уксусная кислота.
200. Перечертить диаграмму состояния неконденсированной системы (рис. 13), обозначить ее поля. Определить состав азеотропной жидкости. Описать последовательность процессов, происходящих при испарении раствора, содержащего 15 % HNO3. Заполнить таблицу 1. Можно ли методом перегонки этого раствора получить чистую азотную кислоту?
201. Перечертить диаграмму состояния неконденсированной системы (рис. 13), обозначить ее поля. Определить состав азеотропной жидкости. Описать последовательность процессов, происходящих при испарении раствора, содержащего 25 % HNO3. Заполнить таблицу 1. Можно ли методом перегонки этого раствора получить чистую азотную кислоту?
202. Перечертить диаграмму состояния неконденсированной системы (рис. 13), обозначить ее поля, дать характеристику компонентов этой системы, описать последовательность фазовых превращений при охлаждении и конденсации паров в системе, содержащей 40 % HNO3, а также при нагревании и испарении раствора, содержащего 75% HNO3.
203. Перечертить диаграмму состояния неконденсированной системы (рис. 13), обозначить ее поля. Определить состав азеотропной жидкости. Описать последовательность процессов, происходящих при испарении раствора, содержащего 55 % HNO3. Заполнить таблицу 1. Можно ли методом перегонки этого раствора получить чистую азотную кислоту?
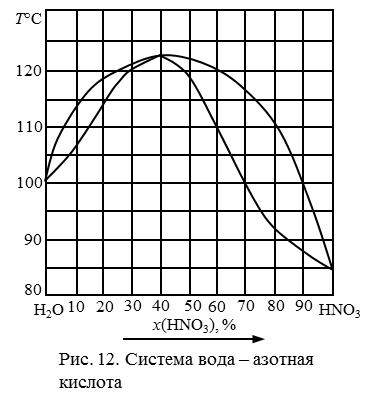
Рис. 13. Диаграмма состояния системы вода – азотная кислота.
204. Определить изменение состава и количества фаз в системе, содержащей 20 % анилина (рис. 14) при охлаждении от 165 до 60°С с интервалом 40°С.
205. Определить изменение состава и количества фаз в системе, содержащей 80 % анилина (рис. 14) при охлаждении от 165 до 60°С с интервалом 40°С.
206. Определить изменение состава и количества фаз в системе, содержащей 60 % анилина (рис. 14) при охлаждении от 165 до 60°С с интервалом 40°С.
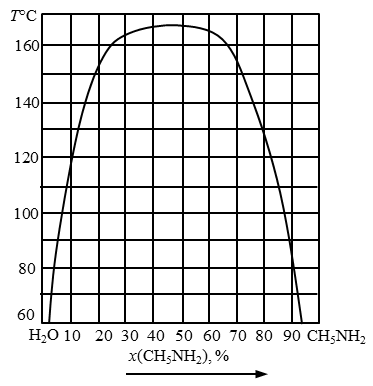
Рис. 14. Диаграмма состояния системы вода – анилин.
207. Определить изменение состава и количества фаз в системе, содержащей 40 % воды (рис. 15) при охлаждении от 220 до 40°С с интервалом 40°С.
208. Определить изменение состава и количества фаз в системе, содержащей 80 % воды (рис. 15) при охлаждении от 165 до 60°С с интервалом 40°С.
209. Определить изменение состава и количества фаз в системе, содержащей 60 % воды (рис. 15) при охлаждении от 165 до 60°С с интервалом 40°С.
210. Определить изменение состава и количества фаз в системе, при температуре 140 °С (рис. 15), содержащей от 0 до 80 % никотина с интервалом 40%.
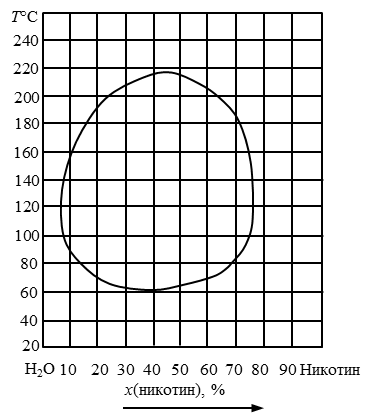
Рис. 15 Диаграмма состояния никотин-вода.
Общая информация
Диаграммы состояния конденсированных систем описывают межфазные равновесия а) между жидкостью и твердым веществом – процессы плавления, растворения, кристаллизации, образования или разрушения химических соединений; б) между разными твердыми фазами - процессы изменения кристаллической структуры вещества или полиморфные превращения, образования твердых растворов. Уравнение правила фаз Гиббса записывается в следующем виде:
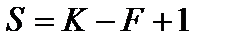 ,
,
где S – число степеней свободы; K – число компонентов; F – количество фаз.
Диаграммы состояния конденсированных систем обычно изображаются в изобарических координатах. По оси абсцисс указан состав системы в мольных или массовых долях (процентах) по компоненту В. По осям ординат указана шкала температур. По линиям А и В показаны температурные точки, характерные для чистых веществ: температуры плавления и полиморфных превращений.
Порядок рассмотрения диаграммы
1. Перечертить диаграмму, соблюдая топологию, в заданном масштабе.
2. Дать общую характеристику диаграммы. При наличии химических соединений вывести их формулу.
3. Отметить линию ликвидуса, линию солидуса, линии растворимости компонентов; написать равновесия на линиях. Составить равновесия на линиях эвтектики и перитектики.
4. Обозначить поля диаграммы греческими или римскими цифрами.
5. Указать фазовый состав полей диаграммы. Начинать следует с определения полей, содержащих одну фазу. Поля, содержащие две фазы находятся обычно между однофазными элементами диаграммы.
6. Описать значимые точки диаграммы (точки плавления компонентов, точки эвтектик, точки перитектик, точки полиморфных превращений и др.): указать температуру, состав, уравнение равновесия.
7. Рассмотреть свойства систем, заданных соответствующими фигуративными точками и заполнить таблицу
| Точка | Исходный состав, % В | Кол-во фаз в точке | Наименование фаз | Состав каждой фазы, % В | Относительное кол-во фаз, % | Температура кристаллизации | Число степеней свободы | |
| ТН | ТK | |||||||
Типовые диаграммы состояния
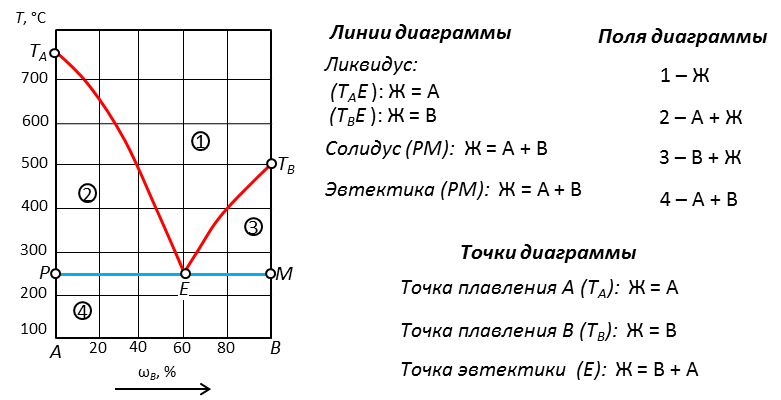
Рис. 16. Диаграмма состояния двухкомпонентной системы с одной точкой эвтектики.
Общая характеристика диаграммы. Есть: неограниченная растворимость компонентов в жидкой фазе. Нет: химических соединений, твердых растворов, полиморфных превращений.
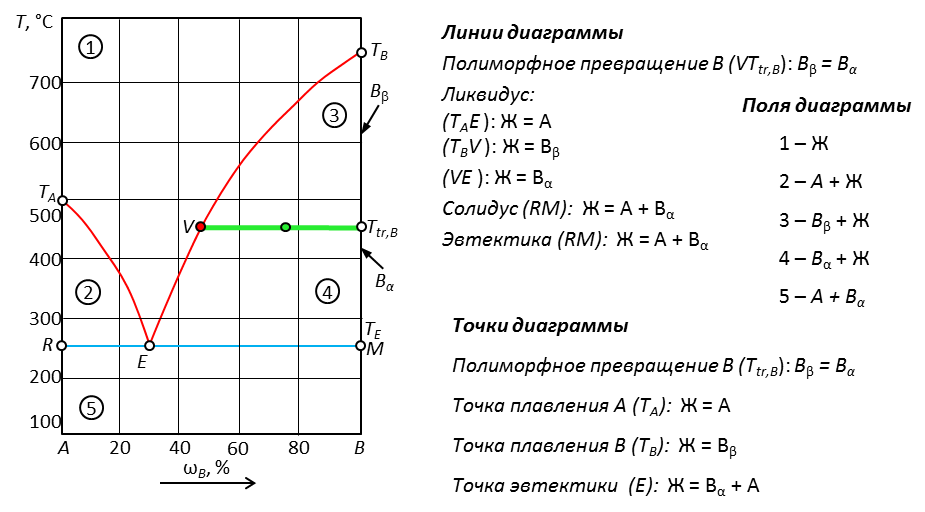
Рис. 17. Диаграмма с полиморфным превращением компонента В
Наличие полиморфного превращения обозначается горизонтальной линией (V- Ttr, B). Начало линии идет от того вещества, которое меняет кристаллическую решетку (от вещества В). Выше линии превращения – одна кристаллическая модификация, ниже – другая.
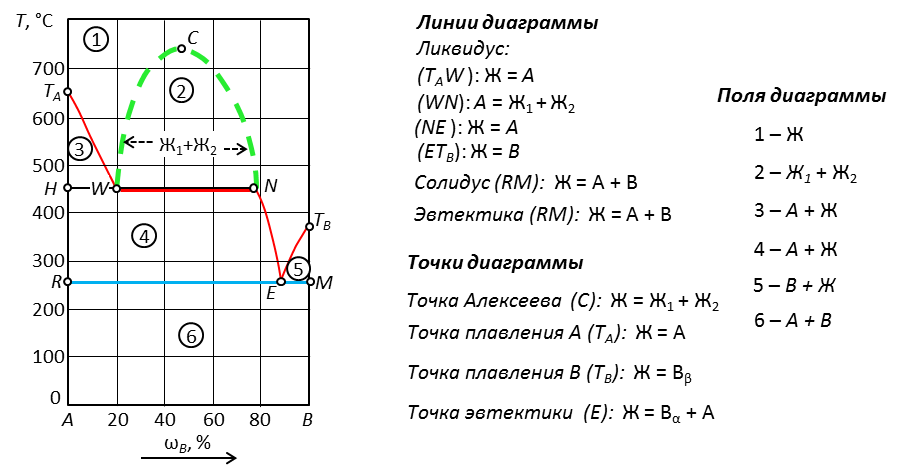
Рис. 18. Диаграмма с ограниченной растворимостью жидкостей
Наличие области ограниченной растворимости жидкостей и их расслаивания на две фазы обозначают пунктирной линией, расположенной выше ликвидуса. Изотерма (WN) показывает начало расслаивания при нагревании системы. Точка Алекссева (С) показывает условия, при которых существует одна жидкая фаза.
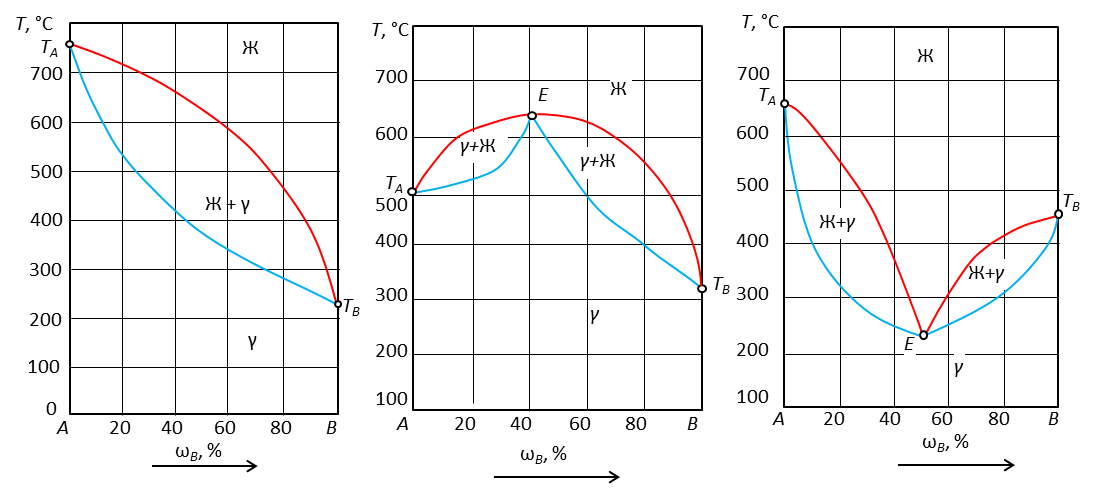
Рис. 19. Диаграммы состояния с твердыми растворами замещения.
Диаграммы просты. Состоят из линий ликвидуса и солидуса. Могут иметь экстремальные точки, а могут и не иметь.
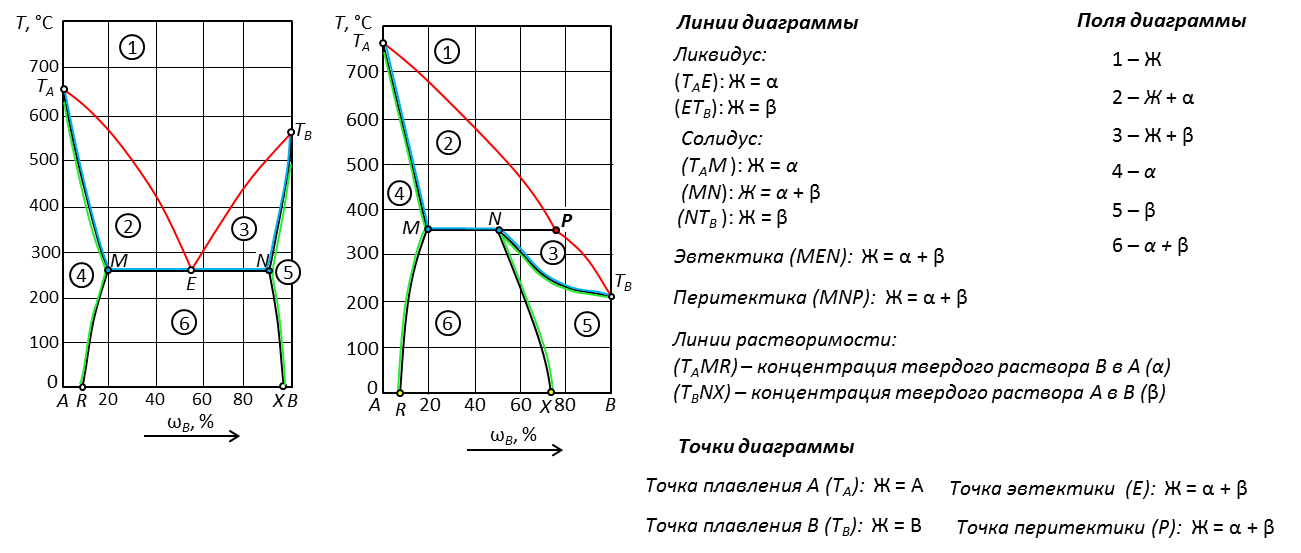
Рис. 20. Диаграммы с твердыми растворами внедрения.
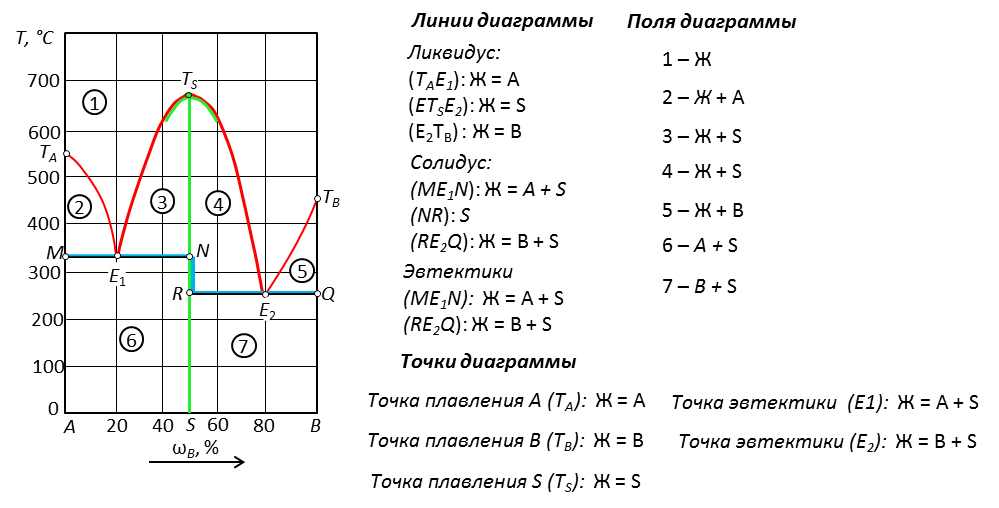
Рис. 21. Диаграмма с химическим соединением постоянного состава, которое плавится без разложения (конгруэнтно).
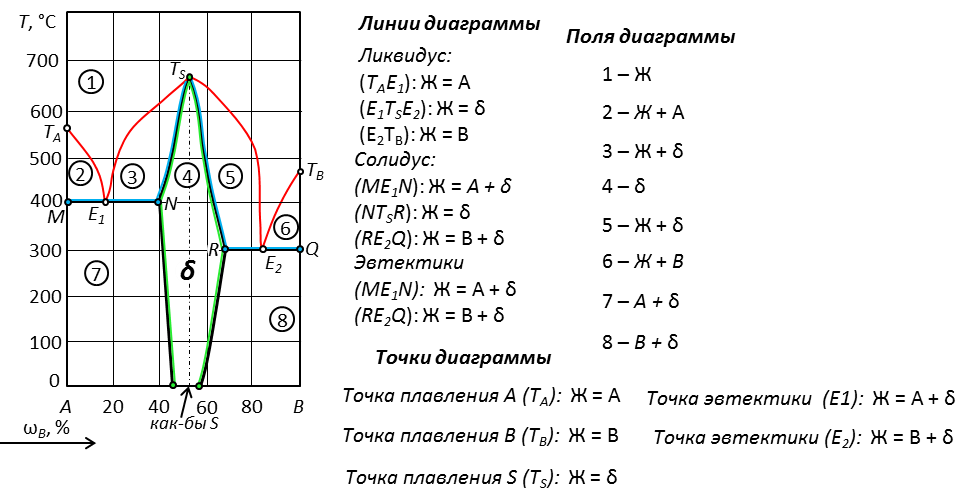
Рис. 22. Диаграмма с дальтонидом, который плавится без разложения
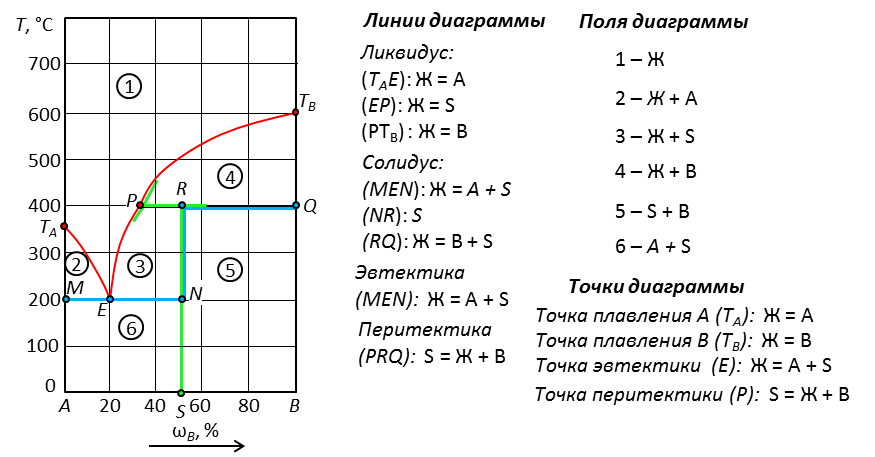
Рис. 23. Химическое соединение постоянного состава, которое плавится с разложением.
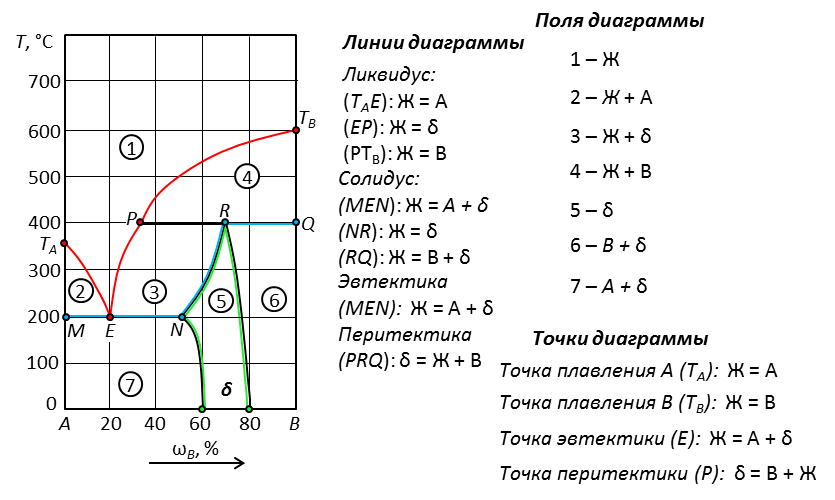
Рис. 24. Химическое соединение переменного состава, которое плавится с разложением. Обозначается на диаграммах как область состава δ, ограниченная линией перитектики.
Примеры решения задач
Пример 11. Прочесть диаграмму состояния системы «медь – магний».

Рис. 16. Диаграмма состояния медь-магний.
Решение. 1. Дать общую характеристику диаграммы состояния.
Температура плавления (кристаллизации) чистой меди ТСu = 1083°С, а магния TMg = 650°С. В расплавленном состоянии эти металлы неограниченно растворимы и образуют одну жидкую фазу. Магний кристаллизуется из двухкомпонентного расплава в чистом виде, а медь – в виде твердого раствора α, область существования которого ограничена пределами от 0 до 5 % Mg и в котором «хозяином» кристаллической решетки является медь. Кристаллические модификации компонентов не меняются.
Медь и магний образуют два химических соединения, плавящиеся без разложения (конгруэнтно). Первое из них содержит от 30 до 37 % магния, плавится при температуре 819°С. Второе химическое соединение S2 плавится при 568°С, имеет постоянный стехиометрический состав, содержит 65 % Mg.
Вывод формул химических соединений. Точке плавления соединения S1 (δ) отвечает мольная доля магния 34 %. Допускают, что количество вещества химического соединения один моль, тогда 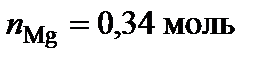 ,
, 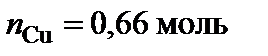 .
. 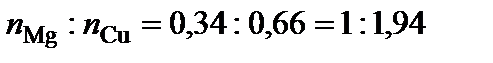 , следовательно, формула химического соединения S1 (δ) – Cu2Mg.
, следовательно, формула химического соединения S1 (δ) – Cu2Mg.
Точке плавления соединения S2 отвечает мольная доля магния 66 %. Допускают, что 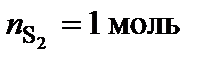 , тогда
, тогда 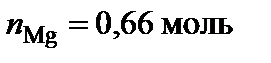 ,
, 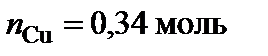 .
. 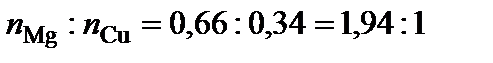 – Mg2Cu.
– Mg2Cu.
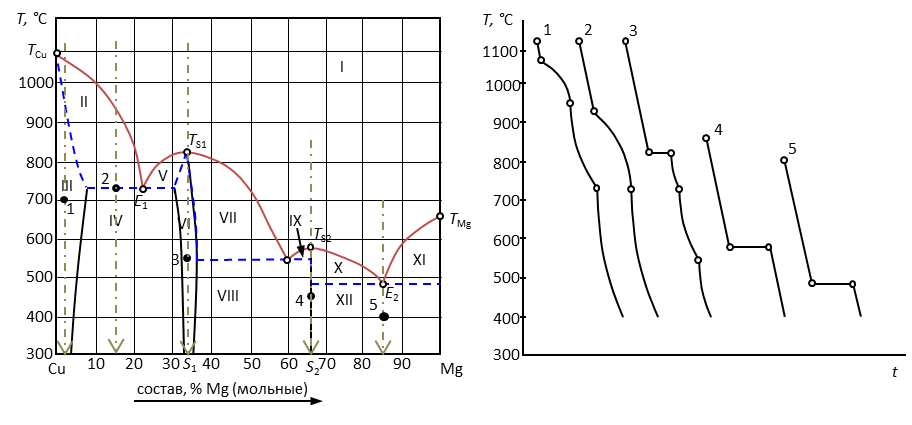
Рис. 17. Решение примера 1.
2. Пронумеровать поля диаграммы и дать их наименование.
I – расплав (Ж); II – Ж + α; III – твердый раствор внедрения магния в меди (α); IV – α + δ; V – δ + Ж; VI – δ; VII – δ + Ж; VIII – δ + S2; IX – Ж + S2; X – Ж + S2; XI – Ж + Mg; XII – Mg + S2.
3.
| № | Состав, % В | Кол-во фаз | Наименование фаз | Состав каждой фазы, %В | Относит. кол-во каждой фазы, % | Т крист. | F | |
| Тн | Тк | |||||||
| 1 | 3 | 1 | α | 3 | 100 | 1090 | 950 | 2-1+1=2 |
| 2 | 15 | 3 | α | 8 | Ж=δ=α | 930 | 730 | 2-3+1=0 |
| Ж | 21 | |||||||
| δ | 30 | |||||||
| 3 | 33 | 1 | δ | 33 | 100 | 820 | 820 | 2-1+1=2 |
| 4 | 65 | 1 | S2 | 65 | 100 | 580 | 580 | 2-1+1=2 |
| 5 | 85 | 2 | S2 | 65 | 43 | 490 | 490 | 2-2+1=1 |
| Mg | 100 | 57 | ||||||
Расчет точки 5
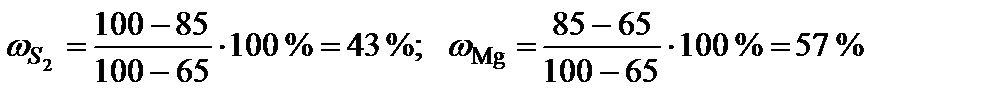
Задачи для решения
211.

212.
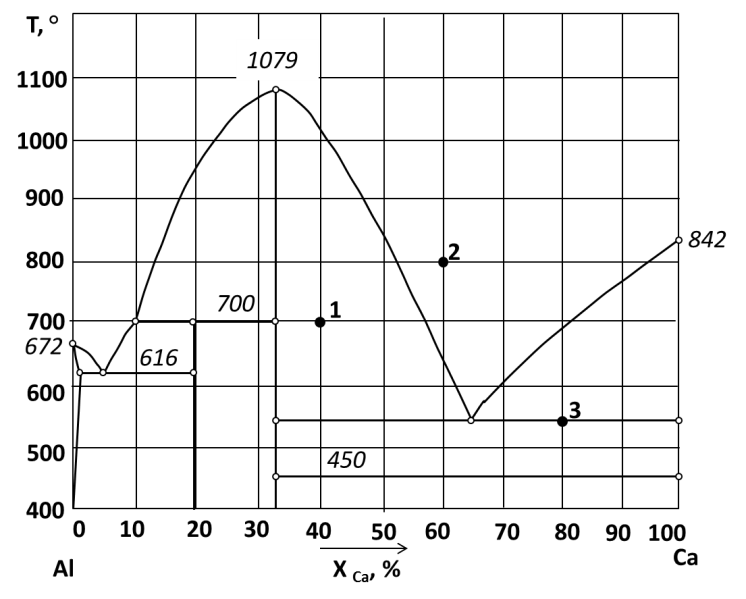
213.

214.

215.

216.

217.

218.

219.

220.

221.

222.

223.

224.

225.
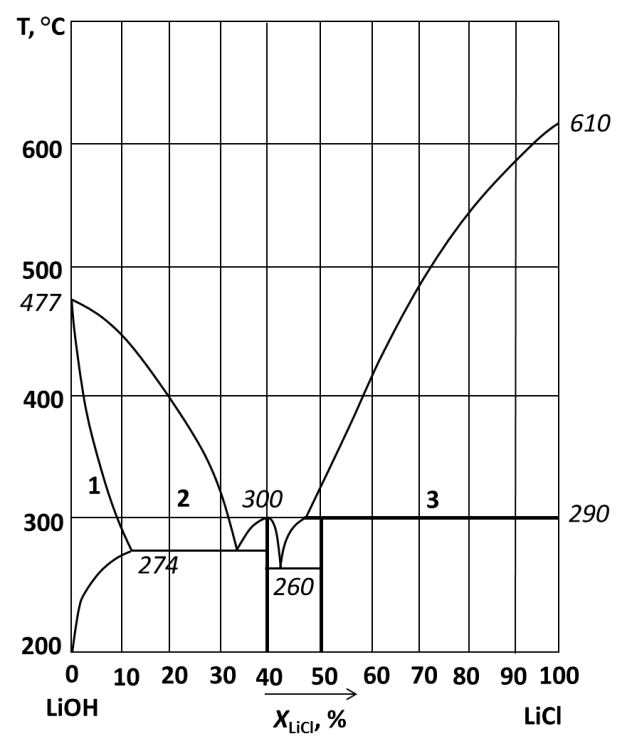
226.

227.

228.
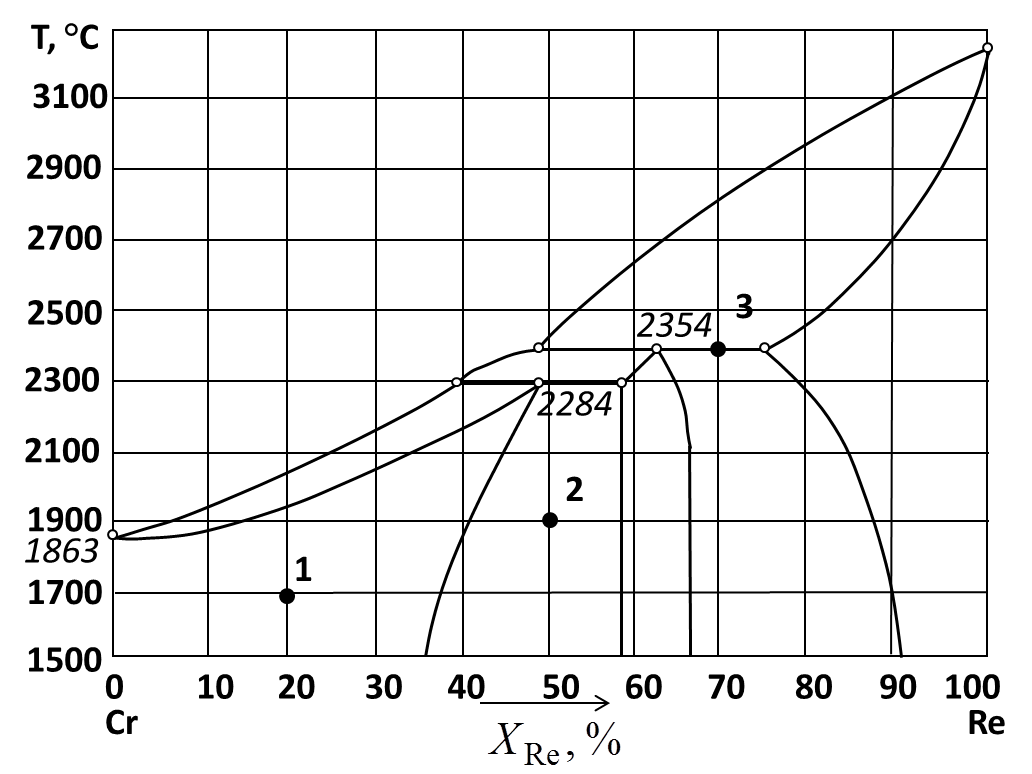
229.

230.

231.

232.

233.

234.

235.

236.

237.

238.

239.

240.

Расчет термодинамических параметров химических реакций
Краткие теоретические сведения
Согласно закону Гесса тепловой эффект реакции не зависит от пути процесса, а определяется только начальным и конечным состояниями системы при условии, что давление и объем в течение всего процесса остаются постоянными, а температура начала и конца процесса одинакова.
Из закона Гесса следует уравнение расчета теплового эффекта химической реакции:
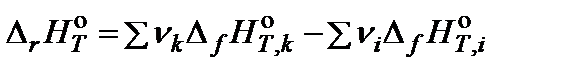 ,
,
где ν – стехиометрический коэффициент; индекс i относится к исходным веществам, индекс k – к продуктам реакции. 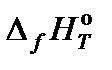 – тепловой эффект образования вещества, приведенный к стандартным условиям при температуре Т.
– тепловой эффект образования вещества, приведенный к стандартным условиям при температуре Т.
За стандартные условия принято состояние вещества в чистом виде при давлении 1 атм. Стандартное состояние вещества отмечается верхним индексом «о». Тепловые эффекты образования веществ для температуры 298 K приводятся в справочной литературе.
При расчете тепловых эффектов химических реакций, протекающих в водных растворах, следует учитывать диссоциацию химических соединений. Для этого следует перейти от молекулярного уравнения реакции к сокращенному ионному уравнению. При составлении ионного уравнения реакции нужно учитывать, что малорастворимые соединения, слабые электролиты (кислоты, основания), оксиды, газообразные вещества на ионы не диссоциируют. Для тех химических соединений, которые диссоциируют в растворе, в расчетах нужно использовать стандартные теплоты образования соответствующих ионов, а для тех, которые не диссоциируют – стандартные теплоты образования соединений.
Зависимость теплового эффекта реакции от температуры описывается уравнением
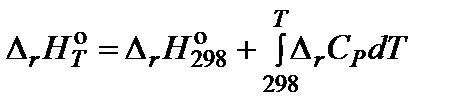 ,
,
Под интегралом находится зависимость теплоемкости от температуры, которая выражается уравнением:
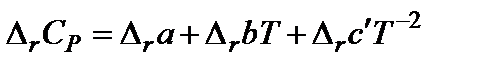 ,
,
Коэффициенты 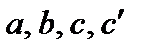 определяют из эксперимента или на основании молекулярно-статистических расчетов и приводят в справочной литературе.
определяют из эксперимента или на основании молекулярно-статистических расчетов и приводят в справочной литературе. 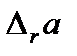 ,
, 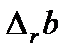 и
и 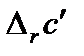 (или
(или 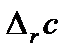 для органических соединений) вычисляют по закону Гесса.
для органических соединений) вычисляют по закону Гесса.
Для определения направления протекания процесса пользуются величиной энергии Гиббса 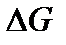 . Энергия Гиббса складывается из изменения энтальпии процесса и так называемого энтропийного фактора:
. Энергия Гиббса складывается из изменения энтальпии процесса и так называемого энтропийного фактора:
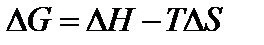 ,
,
где 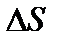 – изменение энтропии.
– изменение энтропии.
Если ΔG < 0, то считается, что процесс термодинамически возможен.
Для изолированных систем энтропия является одним из критериев возможности протекания процесса.
Для расчета изменения энтропии в ходе химической реакции применим закон Гесса:
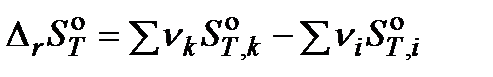 ,
,
где ν – стехиометрический коэффициент; индекс i относится к исходным веществам, индекс k – к продуктам реакции. 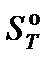 – энтропия образования вещества, приведенная к стандартным условиям при температуре Т.
– энтропия образования вещества, приведенная к стандартным условиям при температуре Т.
Зависимость изменения энтропии химической реакции от температуры описывается уравнением:
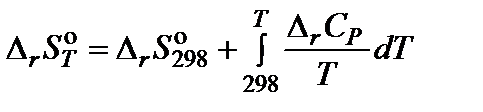 .
.
Примеры решения задач
Пример 1. Вычислить тепловой эффект и изменение энергии Гиббса реакции
K2SO4(aq) + 2AgNO3(aq) = 2KNO3(aq) + Ag2SO4(s),
протекающей в водном растворе, при 298 K.
Решение. Для решения задачи следует перейти от молекулярного уравнения реакции к сокращенному ионному уравнению. При составлении ионного уравнения реакции следует учитывать, что малорастворимые соединения, слабые электролиты (кислоты, основания), оксиды, газообразные вещества на ионы не диссоциируют.
1. Составить полное ионное уравнение для этой реакции, учитывая, что хлорид серебра относится к малорастворимым соединениям (осадок):
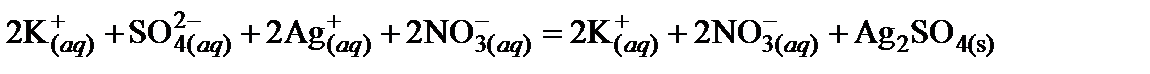 .
.
2. Сократив одинаковые компоненты по обе стороны уравнения, получить сокращенное ионное уравнение:
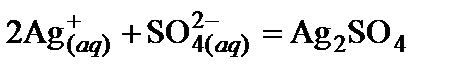 .
.
3. Составить таблицу справочных данных, необходимых для расчета:
| Компонент | Ag2SO4(s) | 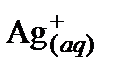
| 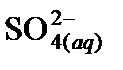
|
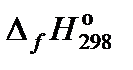 , кДж/моль , кДж/моль
| −715,88 | 105,75 | −909,26 |
 , кДж/моль , кДж/моль
|
4. Составить уравнение для расчета теплового эффекта реакции и выполнить необходимые вычисления:
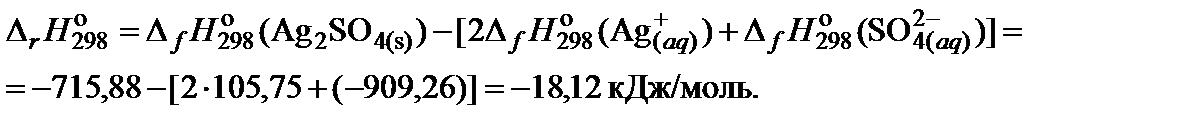
5. Составить уравнение для расчета изменения энергии Гиббса реакции и выполнить необходимые вычисления
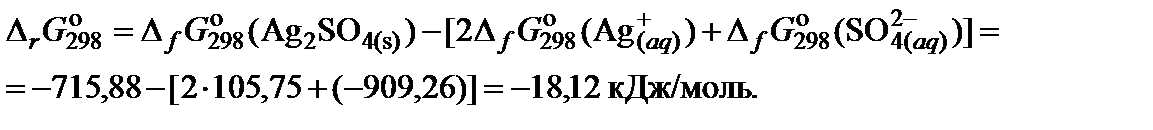
Пример 2. Вычислить изменение энергии Гиббса реакции
4NH3(g) + 5O2(g) = 6H2O(g) + 4NO(g)
при 298 K.
Решение. 1. Составить таблицу справочных данных, необходимых для расчета:
| Компонент | NH3(g) | O2(g) | H2O(g) | NO(g) |
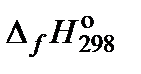 , кДж/моль , кДж/моль
| −45,94 | 0 | −241,81 | 91,26 |
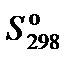 , Дж·моль−1·K−1 , Дж·моль−1·K−1
| 192,66 | 205,04 | 188,72 | 210,64 |
2. Составить уравнение для расчета теплового эффекта реакции и выполнить необходимые вычисления:
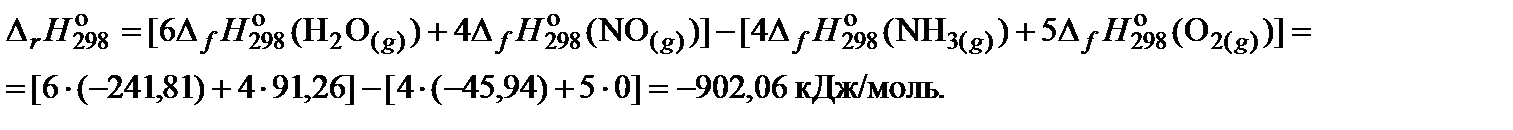
3. Составить уравнение для расчета изменения энтропии реакции в соответствии с законом Гесса и выполнить необходимые вычисления:
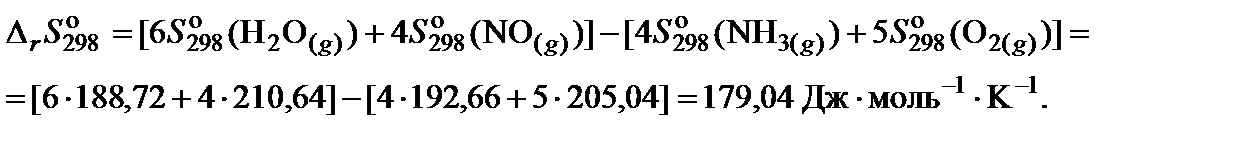
4. Вычислить изменение энергии Гиббса, учитывая разность в размерности теплового эффекта и энтропии:
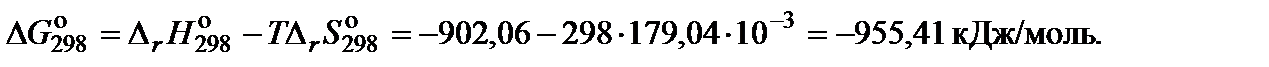
Пример 3 . Вычислить изменение энергии Гиббса при 850 K для реакции
4NH3(g) + 5O2(g) = 6H2O(g) + 4NO(g).
Решение. 1. Составить таблицу справочных данных, необходимых для расчета:
| Компонент | NH3(g) | O2(g) | H2O(g) | NO(g) |
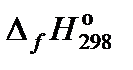 , кДж/моль , кДж/моль
| −45,94 | 0 | −241,81 | 91,26 |
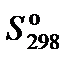 , Дж·моль−1·K−1 , Дж·моль−1·K−1
| 192,66 | 205,04 | 188,72 | 210,64 |
| a, Дж·моль−1·K−1 | 29,80 | 31,46 | 30,00 | 29,58 |
| b·103, Дж·моль−1·K−1 | 25,48 | 3,39 | 10,71 | 3,85 |
| c’·10−5, Дж·моль−1·K−1 | −1,67 | −3,77 | 0,33 | −0,59 |
2. Пользуясь законом Гесса, найти изменение коэффициентов теплоемкости в ходе процесса:
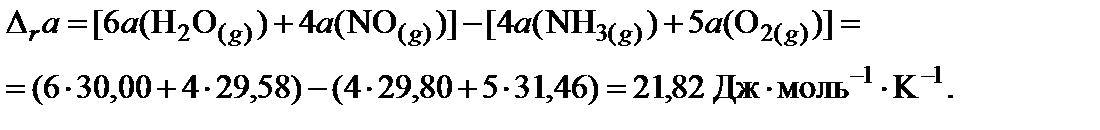
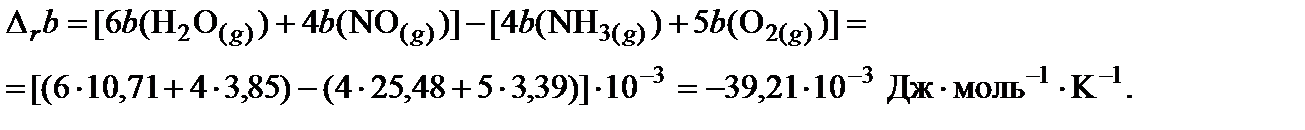
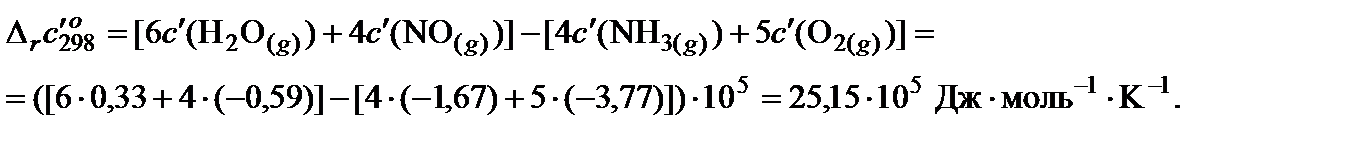
3. Вычислить тепловой эффект реакции при 850 K:
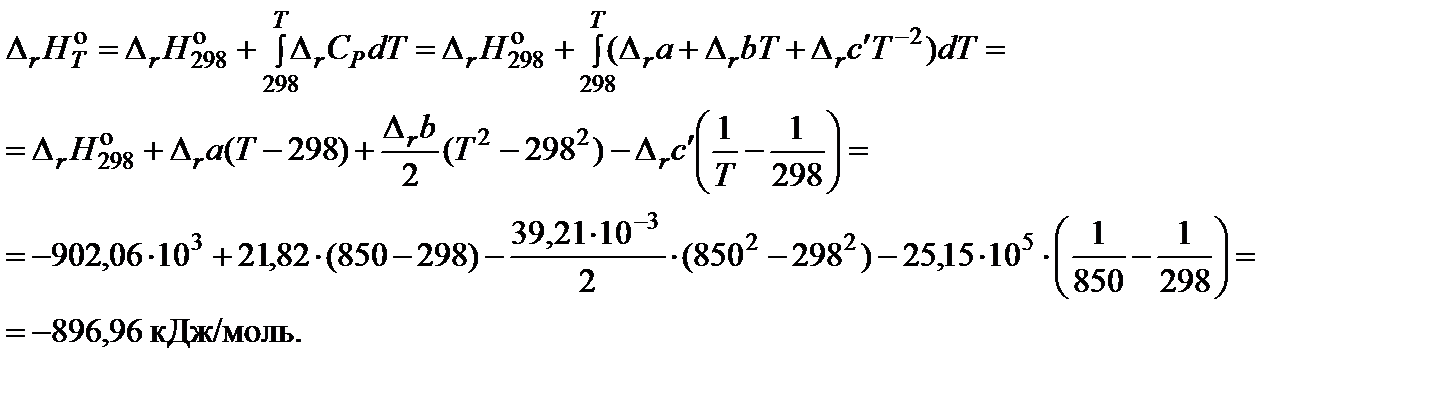
4. Вычислить изменение энтропии реакции при 850 K:
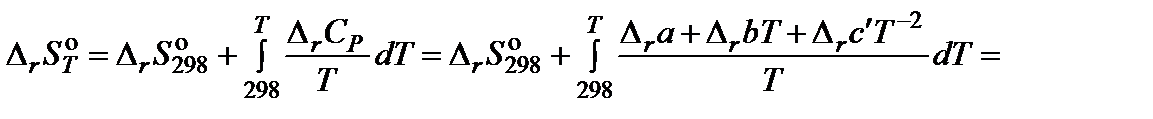
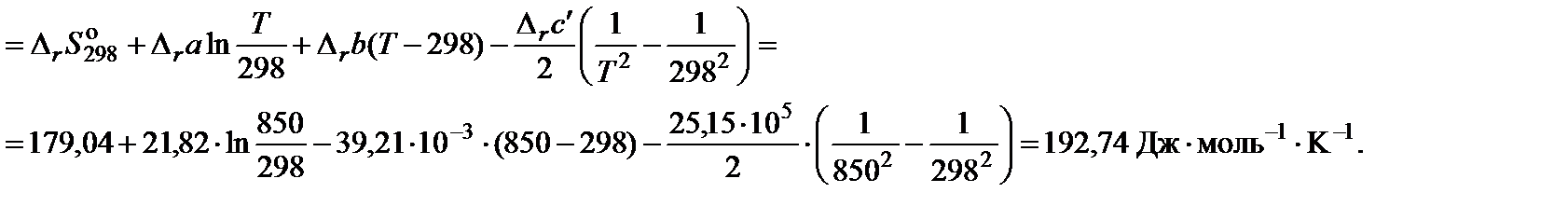
5. Вычислить изменение энергии Гиббса, учитывая размерности теплового эффекта и энтропии:
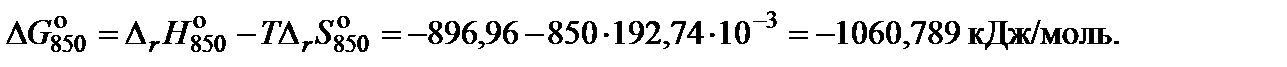
Задачи для решения
Дата: 2019-03-05, просмотров: 990.