Теория вероятностей появилась в XV веке, в эпоху Возрождения, когда азартные игры – игральная кость, карты – были особенно распространены. Первыми выдающимися учеными в этой области науки были: Л. Пачоли (1445-1510), Н. Тарталья (1449-1557) и Дж. Кардано (1501-1576). Даже такие крупные ученые как Г. Галилей (1564-1642), Б. Паскаль (1623-1662), П. Ферма (1601-1665) и Ч. Чейгенс (1629-2695) занимались проблемами азартных игр. Развитие торговли, возросшее значения выигрыша и риска в торговле, страхование, возникающее в связи с развитием судоходства, также способствовали созданию теории вероятностей.

Важным этапом истории теории вероятностей является посмертное издание книги “Ars conjectandi” (Искусство догадок) Я. Бернулли (1654-1705). В этой книге дается общее представление о теории вероятностей, открывается закон о больших числах и обосновывается математическая теория вероятностей. Позже Муавром (1667-1751), Байесом (1702-1761) и Лапласом (1749-1827) были достигнуты такие результаты, которые широко применяются и в наши дни. Многое сделали в разработке теории вероятностей такие ученые как К.Ф. Гаусс (1777-1855), А.М. Лежандр (1752-1833) и Д. Пуассон (1781-1840). Дальнейшее развитие теория вероятностей получила только во второй половине XIX века в работах великих русских математиков П.Л. Чебышев (1821-1894), А.А. Маркова (1856-1922) и А.М. Ляпунова (1857-1918). Начало математической статистике было положено в Англии в начале XX века.

Долгое время теория вероятностей не считалась равноценной другим областям математики, так как не были в достаточной степени выяснены ее принципиальные основы. Это обстоятельство тормозило развитие естественных наук, особенно развитие современной физики.

Огромный вклад в аксиоматическое построение теории вероятностей был внесен математиком А.Н. Колмогоровым (год рождения 1902) в 1933 г. Его достижения в разработке теории вероятностей сделали ее одной и важнейших глав математики, результаты которой применяются в различных областях математички и, наоборот, многие выводы математической дисциплины находят применение в теории вероятностей.

 За 20 лет круг применения теории вероятностей значительно расширился в связи с развитием атомной физики, техники, связи и автоматизации. Результаты теории вероятностей широко применяются в решении как теоретических, так и практических задач, связанных с работой электронно-вычислительных машин.

В последнее время теория вероятностей продолжает занимать видное положение. Кроме упомянутого выше А.Н. Колмогорова должны быть названы, прежде всего, имена С.Н. Бернштейна, А.Я. Хинчина, Б.В. Гнеденко и А.Н. Вендель.

В частности, в области математической статистики наиболее активными представителями являются А.Н. Ширяев, Р.Ш. Липцер и М.П. Ершов.

18. Примеры для самостоятельной работы

1. Выборка задана в виде распределения частот

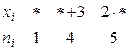
Найти распределение относительных частот.

2. Найти эмпирическую функцию по данному распределению выборки:

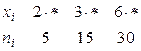
3. Построить полигон частот по данному распределению выборки:

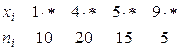
4. Построить гистограмму частот по данному распределению выборки объема .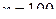

№ интервала	Частотный  интервал	Сумма частот	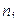Плотность
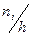
1		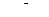10
2		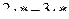20
3		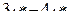45
4		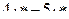15
5		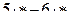10

5. Из генеральной совокупности извлечена выборка объема :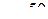

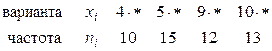
Найти несмещенную оценку генеральной средней.

6. Найти выборочную среднюю и выборочную дисперсию по данному распределению выборки объема :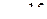

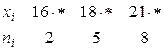
7. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема :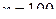

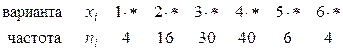
8. Найти методом сумм выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема :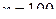

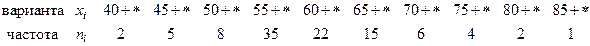
9. Найти методом произведений асимметрию и эксцесс по заданному распределению выборки объема :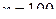

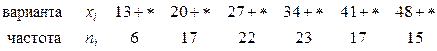
10.  Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема :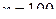

.

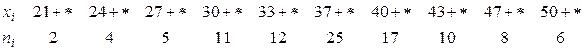Где * - последняя цифра шифра.