Эмпирической функцией распределения (функцией распределения выборки) называют функцию  , определяющую для каждого значения
, определяющую для каждого значения 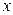 относительную частоту события
относительную частоту события 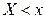 :
:
 , (5.1)
, (5.1)
где  - число вариант, меньших
- число вариант, меньших 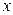 ;
;
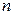 - объем выборки.
- объем выборки.
Свойства эмпирической функции:
Свойство 1. Значения эмпирической функции принадлежат отрезку  .
.
Свойство 2.  - неубывающая функция.
- неубывающая функция.
Свойство 3. Если  - наименьшая варианта, а
- наименьшая варианта, а 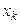 - наибольшая, то
- наибольшая, то
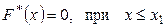
и
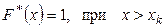 .
.
Пример 5.1. Найти эмпирическую функцию по данному распределению выборки:
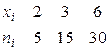 .
.
Решение. Найдем объем выборки 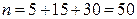 .
.
Наименьшая варианта 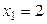 , поэтому
, поэтому 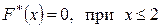 .
.
Значение 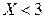 , а именно
, а именно 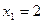 наблюдалось 5 раз, следовательно,
наблюдалось 5 раз, следовательно,
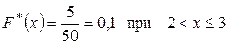 .
.
Значение 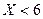 , а именно:
, а именно: 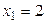 и
и 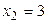 наблюдалось 5+15=20 раз:
наблюдалось 5+15=20 раз:
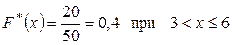 .
.
Так как 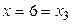 - наибольшая варианта, то
- наибольшая варианта, то 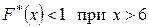 .
.
Искомая эмпирическая функция:
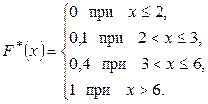 .
.
График этой эмпирической функции:
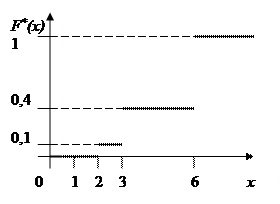
Рис. 5.1. График эмпирической функции
Полигон и гистограмма
6.1. Дискретное распределение признака  .
.
Полигоном частот называют ломаную, отрезки которой соединяют точки 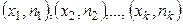 , где
, где  - варианты выборки и
- варианты выборки и 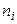 - соответствующие им частоты.
- соответствующие им частоты.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 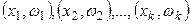 , где
, где  - варианты выборки и
- варианты выборки и 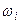 соответствующие им относительные частоты [2].
соответствующие им относительные частоты [2].
6.2. Непрерывное распределение признака  .
.
При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины 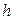 и находят
и находят 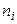 - сумму частот вариант, попавших в
- сумму частот вариант, попавших в 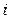 -й интервал.
-й интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 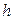 , а высоты равны отношению
, а высоты равны отношению 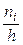 (плотность относительной частоты). Площадь частичного
(плотность относительной частоты). Площадь частичного 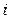 -го прямоугольника равна
-го прямоугольника равна  - относительной частоте вариант, попавших в
- относительной частоте вариант, попавших в 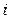 -й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Пример 6.2.1. Построить полигон частот по данному распределению выборки:
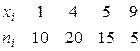 .
.
Решение. Отложим на оси абсцисс варианты  , а на оси ординат – соответствующие им частоты
, а на оси ординат – соответствующие им частоты 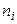 , соединив точки
, соединив точки 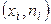 отрезками прямых, получим искомый полигон частот (рис.6.2.1).
отрезками прямых, получим искомый полигон частот (рис.6.2.1).
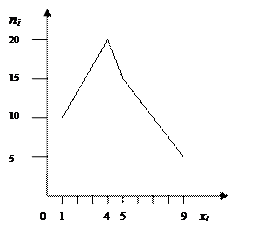
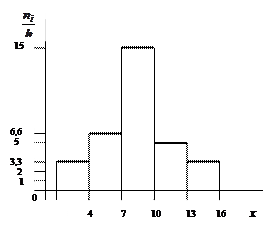
Рис.6.2.1. Полигон частот Рис.6.2.2. Гистограмма частот
Пример 6.2.2. Построить гистограмму частот по данному распределению выборки объема 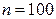 :
:
| Номер интервала | Частичный интервал
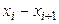 , длиною , длиною 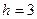
| Сумма частот вариант
интервала 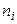
| Плотность
частоты 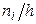
|
| 1 2 3 4 5 | 1-4 4-7 7-10 10-13 13-16 | 10 20 45 15 10 | 3,3 (3) 6,6 (6) 15 5 3,3 (3) |
Решение. Построим на оси абсцисс заданные интервалы длины 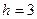 . Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты
. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты 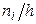 . Например, над интервалом
. Например, над интервалом 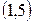 построим отрезок, параллельный оси абсцисс, на расстоянии
построим отрезок, параллельный оси абсцисс, на расстоянии 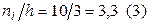 . Аналогично строят остальные отрезки. Искомая гистрограмма частот изображена на рис.6.2.2.
. Аналогично строят остальные отрезки. Искомая гистрограмма частот изображена на рис.6.2.2.
Точечные оценки
Статистической оценкой 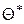 неизвестного параметра
неизвестного параметра 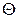 теоретического распределения называют функцию
теоретического распределения называют функцию 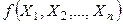 от наблюдаемых случайных величин
от наблюдаемых случайных величин  [1].
[1].
Точечной называют статистическую оценку, которая определяется одним числом 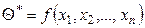 , где
, где 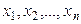 - результаты
- результаты 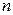 наблюдений над количественным признаком
наблюдений над количественным признаком 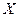 (выборка).
(выборка).
Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
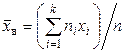 , (7.1)
, (7.1)
где  - варианта выборки,
- варианта выборки, 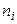 - частота варианты
- частота варианты  ,
, 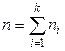 - объем выборки.
- объем выборки.
Замечание 1. Если первоначальные варианты  - большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число
- большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число 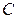 , т.е. перейти к условным вариантам
, т.е. перейти к условным вариантам  (в качестве
(в качестве 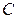 выгодно принять число, близкое к выборочной средней. Поскольку выборочная средняя неизвестна, число
выгодно принять число, близкое к выборочной средней. Поскольку выборочная средняя неизвестна, число 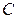 выбирают «на глаз»). Тогда
выбирают «на глаз»). Тогда
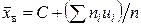 . (7.2)
. (7.2)
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
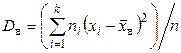 ; (7.3)
; (7.3)
эта оценка является смещенной, так как
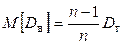 . (7.4)
. (7.4)
Более удобна формула
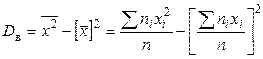 . (7.5)
. (7.5)
Замечание 2. Если первоначальные варианты  - большие числа, то целесообразно вычесть из всех вариант одно и то же число
- большие числа, то целесообразно вычесть из всех вариант одно и то же число 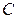 , равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам
, равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам  (дисперсия при этом не изменится). Тогда
(дисперсия при этом не изменится). Тогда
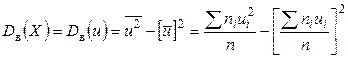 . (7.6)
. (7.6)
Замечание 3. Если первоначальные варианты являются десятичными дробями с  десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число
десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число  , т.е. переходят к условным вариантам
, т.е. переходят к условным вариантам 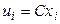 . При этом, дисперсия увеличивается в
. При этом, дисперсия увеличивается в 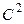 раз, поэтому, найдя дисперсию условных вариант, надо разделить ее на
раз, поэтому, найдя дисперсию условных вариант, надо разделить ее на 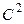 :
:
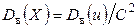 . (7.7)
. (7.7)
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
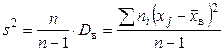 . (7.8)
. (7.8)
Более удобная формула
 . (7.9)
. (7.9)
В условных вариантах она имеет вид
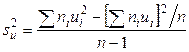 , (7.10)
, (7.10)
причем если  , то
, то 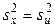 ; если
; если 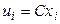 , то
, то 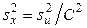 .
.
Замечание 4. При большом числе данных используют метод произведений или метод сумм.
Пример 7.1. Из генеральной совокупности извлечена выборка объема 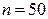 :
:
 .
.
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя
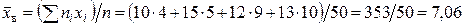 .
.
Пример 7.2. Найти выборочную среднюю по данному распределению выборки объема 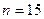 :
:
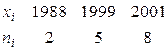 .
.
Решение. Первоначальные варианты – большие числа, поэтому перейдем к условным вариантам 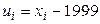 . В итоге получим распределение условных вариант:
. В итоге получим распределение условных вариант:
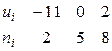 .
.
Найдем искомую выборочную среднюю:
 .
.
Пример 7.3. Найти выборочную дисперсию по данному распределению выборки объема 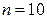 :
:
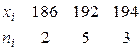 .
.
Решение. Варианты – сравнительно большие числа, поэтому перейдем к условным вариантам 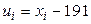 (мы вычли из вариант число
(мы вычли из вариант число 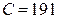 , близкое к выборочной средней). В итоге получим распределение условных вариант:
, близкое к выборочной средней). В итоге получим распределение условных вариант:
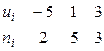 .
.
Найдем искомую выборочную дисперсию:

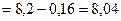 .
.
Метод моментов
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.
Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка:  . Учитывая, что
. Учитывая, что  и
и 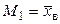 , получим
, получим
 . (8.1)
. (8.1)
Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (8.1) относительно неизвестного параметра, тем самым получим его точечную оценку.
Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:
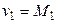 ,
,  .
.
Учитывая, что 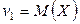 ,
, 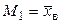 ,
,  ,
, 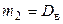 , имеем
, имеем
 (8.2)
(8.2)
Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (8.2) относительно неизвестных параметров, тем самым получим их точечные оценки.
Разумеется, для вычисления выборочной средней  и выборочной дисперсии
и выборочной дисперсии 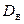 надо располагать выборкой
надо располагать выборкой 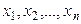 .
.
Пример 8.1. Случайная величина 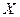 распределена по закону Пуассона
распределена по закону Пуассона
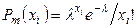 ,
,
где 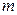 - число испытаний, произведенных в одном опыте;
- число испытаний, произведенных в одном опыте; 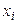 - число появлений события в
- число появлений события в 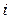 -м опыте.
-м опыте.
Найти методом моментов по выборке 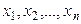 точечную оценку неизвестного параметра
точечную оценку неизвестного параметра 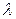 , определяющего распределение Пуассона.
, определяющего распределение Пуассона.
Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравняем начальный теоретический момент первого порядка 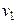 начальному эмпирическому моменту первого порядка
начальному эмпирическому моменту первого порядка 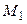 :
:
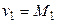 .
.
Приняв во внимание, что 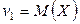 ,
, 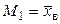 , получим
, получим 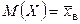 . Учитывая, что математическое ожидание распределения Пуассона равно параметру
. Учитывая, что математическое ожидание распределения Пуассона равно параметру 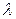 этого распределения, окончательно имеем
этого распределения, окончательно имеем 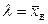 .
.
Итак, точечной оценкой параметра 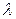 распределения Пуассона служит выборочная средняя:
распределения Пуассона служит выборочная средняя: 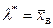 .
.
Пример 8.2. Найти методом моментов по выборке 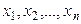 точечные оценки неизвестных параметров
точечные оценки неизвестных параметров  и
и 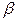 гамма-распределения, плотность которого
гамма-распределения, плотность которого
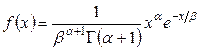
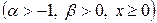 .
.
Решение. Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка 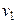 начальному эмпирическому моменту первого порядка
начальному эмпирическому моменту первого порядка 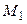 и центральный теоретический момент второго порядка
и центральный теоретический момент второго порядка 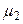 центральному эмпирическому моменту второго порядка
центральному эмпирическому моменту второго порядка 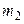 :
:
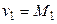 ,
,  .
.
Учитывая, что 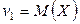 ,
, 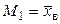 ,
,  ,
, 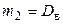 , имеем
, имеем
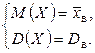 (8.3)
(8.3)
Математическое ожидание и дисперсия гамма-распределения соответственно равны  ,
,  , поэтому (8.3) можно записать в виде
, поэтому (8.3) можно записать в виде
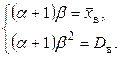
Решив эту систему, окончательно получим искомые точечные оценки неизвестных параметров: 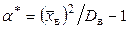 ,
, 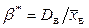 .
.
Дата: 2019-03-05, просмотров: 416.