З адача математической статистики
В теории вероятностей обычно исходят из того, что известны или вероятность некоторых более простых событий, или функции распределения некоторых случайных переменных. При подбрасывании монеты, например, нам известно (как предварительное условие), что подбрасываемая монета имеет симметричную форму. Но это не доказано нами. Может возникнуть вопрос: «Имеет ли подбрасываемая монета действительно симметричную форму?». Симметричность монеты может быть проверена применением некоторого физического метода. Если данная монета подбрасывается много раз подряд и орел выпадает примерно в половине всех экспериментов, то можно предположить, что монета является симметричной. Чтобы высказать такое предположение, необходимо определить, что подразумевается под термином «монета подбрасывается много раз» и «примерно в половине». С помощью математической статистики можно ответить на эти вопросы, так как ее задачей является определение на основе результатов экспериментов вероятности некоторых событий, функции плотности случайных переменных, математического ожидания, дисперсии и других характерных черт. Но бывает (небольшая вероятность), что монета выпадет на орел много раз подряд; в таком случае принимается решение: монета не имеет симметричную форму. Но может случиться, что монета несимметричной формы выпадает на орел именно в половине первой части экспериментов и в этом случае также принимается ошибочное решение. На основе применения методов математической статистики можно утверждать о правильности решения с большой вероятностью.
Исследование гипотез
Часто приходится отвечать на вопрос о правильности или неправильности некоторой гипотезы. Например, если на каком-то заводе приняли определенную партию товара, то не обязательно знать точно, сколько процентов составляют бракованные предметы в партии товара. Обычно достаточно определить, что относительное количество бракованного товара больше или меньше чем 3%. В первом случае партия товара будет отвергнута, а во втором – принята. Для реализации исследований статистических гипотез служат статистические пробы.
Проба 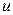 . Пусть
. Пусть 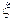 представляет собой случайную переменную с нормальным распределением, с известной дисперсией
представляет собой случайную переменную с нормальным распределением, с известной дисперсией 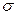 . Надо проверить такую гипотезу, равняется ли математическое ожидание случайной величины
. Надо проверить такую гипотезу, равняется ли математическое ожидание случайной величины 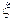 определенному числу
определенному числу 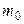 .
.
Для контроля данной гипотезы выбирается проба из 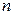 элементов таким образом, что элементы пробы выбираются независимо друг от друга. Пусть результатом снятий проб будут величины
элементов таким образом, что элементы пробы выбираются независимо друг от друга. Пусть результатом снятий проб будут величины 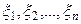 . Проведем расчет величины
. Проведем расчет величины
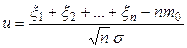 . (2.1)
. (2.1)
Можно увидеть, что случайная переменная 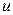 имеет нормальное распределение, дисперсию 1; если выполняется гипотеза
имеет нормальное распределение, дисперсию 1; если выполняется гипотеза 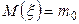 , то
, то 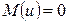 . Таким образом, при выполнении данной гипотезы действительно следующее соотношение:
. Таким образом, при выполнении данной гипотезы действительно следующее соотношение:
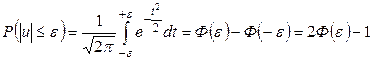 . (2.2)
. (2.2)
Пусть 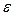 будет таким, что можно было выполнить соотношение
будет таким, что можно было выполнить соотношение
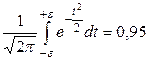 . (2.3)
. (2.3)
В таком случае, если из пробы получено такое значение 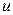 , абсолютная величина которого больше чем
, абсолютная величина которого больше чем 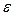 , то гипотеза
, то гипотеза 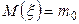 может быть отвергнута, так как произошло событие, которое является невероятным при правильности гипотезы. Иными словами, если гипотеза
может быть отвергнута, так как произошло событие, которое является невероятным при правильности гипотезы. Иными словами, если гипотеза 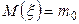 отвергнута при выполнении условия
отвергнута при выполнении условия 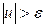 , то только в 5% всех случаев будет отвергнута правильная гипотеза.
, то только в 5% всех случаев будет отвергнута правильная гипотеза.
Бывает и так, что гипотеза 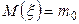 не выполняется и все-таки принимается решение о правильности гипотезы. Вероятность ошибки такого рода нельзя определить так просто, как в случае проявления ошибки другого характера. Ибо в этом случае, если
не выполняется и все-таки принимается решение о правильности гипотезы. Вероятность ошибки такого рода нельзя определить так просто, как в случае проявления ошибки другого характера. Ибо в этом случае, если 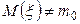 , все равно
, все равно 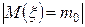 представляет собой малую величину. В таком случае более вероятно, что мы примем неправильную гипотезу
представляет собой малую величину. В таком случае более вероятно, что мы примем неправильную гипотезу 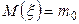 , чем в том случае, когда
, чем в том случае, когда 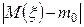 имеет очень большое значение. В случае, если
имеет очень большое значение. В случае, если 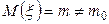 , гипотеза принимается с вероятностью
, гипотеза принимается с вероятностью
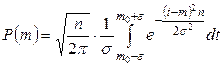 . (2.4)
. (2.4)
Данная формула показывает, что если значение 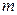 близко к значению
близко к значению 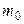 , то с вероятностью
, то с вероятностью 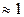 принимается гипотеза
принимается гипотеза 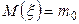 ; если значение
; если значение 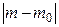 велико, то гипотеза отвергается с вероятностью
велико, то гипотеза отвергается с вероятностью 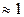 .
.
Функция 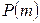 называется силовой функцией пробы.
называется силовой функцией пробы.
Проба 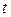 . При использовании пробы
. При использовании пробы 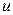 незнание дисперсии обычно представляет собой серьезное затруднение. Пусть
незнание дисперсии обычно представляет собой серьезное затруднение. Пусть 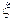 означает случайную переменную с нормальным распределением. Проверяется гипотеза о том, равняется ли математическое ожидание случайной переменной
означает случайную переменную с нормальным распределением. Проверяется гипотеза о том, равняется ли математическое ожидание случайной переменной 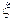 определенному числу
определенному числу 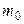 . Проведем
. Проведем 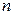 экспериментов, результаты которых обозначим знаками
экспериментов, результаты которых обозначим знаками 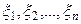 . Оценивается значение выражения
. Оценивается значение выражения
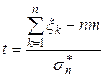 , (2.5)
, (2.5)
где
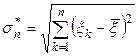 (2.6)
(2.6)
и
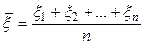 . (2.7)
. (2.7)
Функция распределения случайной переменной 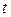 оценивается просто и ее значения могут быть собраны в таблицах. Имея таблицы, можно решить вопрос о правильности гипотезы
оценивается просто и ее значения могут быть собраны в таблицах. Имея таблицы, можно решить вопрос о правильности гипотезы 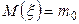 , как это было показано при представлении пробы
, как это было показано при представлении пробы 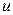 .
.
При применении подобных проб можно решить вопрос о принятии или отклонении других статических гипотез. Ниже приведены только некоторые виды гипотез, для которых уже разработаны пробы.
Часто бывают такие случаи, когда необходимо знать закон распределения случайной переменной, а иногда закон распределения известен, но неизвестны его параметры. В таких случаях выдвигают гипотезу либо о законе распределения, либо гипотезу, связанную с параметрами закона распределения.
Наряду с выдвинутой гипотезой, рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.
Выдвинутую гипотезу называют нулевой (основной).
Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой.
Различают гипотезы, которые содержат только одно и более одного предположений.
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.
Статистическим критерием (или просто критерием) называют случайную величину, которая служит для проверки нулевой гипотезы.
Наблюдаемым значением называют значение критерия, вычисленное по выборкам.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (область допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Поскольку критерий – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.
В приложениях 5-9 приведены значения критических точек распределения 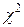 , Стьюдента, Фишера-Снедекора, Кохрена [4].
, Стьюдента, Фишера-Снедекора, Кохрена [4].
Полигон и гистограмма
6.1. Дискретное распределение признака  .
.
Полигоном частот называют ломаную, отрезки которой соединяют точки 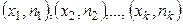 , где
, где  - варианты выборки и
- варианты выборки и 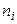 - соответствующие им частоты.
- соответствующие им частоты.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 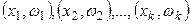 , где
, где  - варианты выборки и
- варианты выборки и 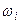 соответствующие им относительные частоты [2].
соответствующие им относительные частоты [2].
6.2. Непрерывное распределение признака  .
.
При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины 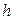 и находят
и находят 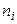 - сумму частот вариант, попавших в
- сумму частот вариант, попавших в 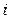 -й интервал.
-й интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 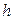 , а высоты равны отношению
, а высоты равны отношению 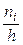 (плотность относительной частоты). Площадь частичного
(плотность относительной частоты). Площадь частичного 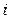 -го прямоугольника равна
-го прямоугольника равна  - относительной частоте вариант, попавших в
- относительной частоте вариант, попавших в 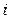 -й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Пример 6.2.1. Построить полигон частот по данному распределению выборки:
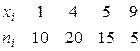 .
.
Решение. Отложим на оси абсцисс варианты  , а на оси ординат – соответствующие им частоты
, а на оси ординат – соответствующие им частоты 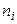 , соединив точки
, соединив точки 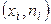 отрезками прямых, получим искомый полигон частот (рис.6.2.1).
отрезками прямых, получим искомый полигон частот (рис.6.2.1).
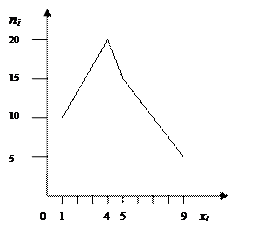
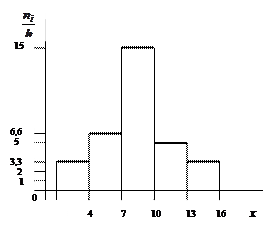
Рис.6.2.1. Полигон частот Рис.6.2.2. Гистограмма частот
Пример 6.2.2. Построить гистограмму частот по данному распределению выборки объема 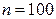 :
:
| Номер интервала | Частичный интервал
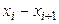 , длиною , длиною 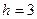
| Сумма частот вариант
интервала 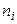
| Плотность
частоты 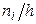
|
| 1 2 3 4 5 | 1-4 4-7 7-10 10-13 13-16 | 10 20 45 15 10 | 3,3 (3) 6,6 (6) 15 5 3,3 (3) |
Решение. Построим на оси абсцисс заданные интервалы длины 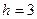 . Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты
. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты 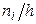 . Например, над интервалом
. Например, над интервалом 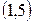 построим отрезок, параллельный оси абсцисс, на расстоянии
построим отрезок, параллельный оси абсцисс, на расстоянии 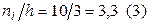 . Аналогично строят остальные отрезки. Искомая гистрограмма частот изображена на рис.6.2.2.
. Аналогично строят остальные отрезки. Искомая гистрограмма частот изображена на рис.6.2.2.
Точечные оценки
Статистической оценкой 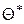 неизвестного параметра
неизвестного параметра 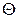 теоретического распределения называют функцию
теоретического распределения называют функцию 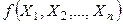 от наблюдаемых случайных величин
от наблюдаемых случайных величин  [1].
[1].
Точечной называют статистическую оценку, которая определяется одним числом 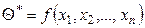 , где
, где 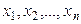 - результаты
- результаты 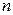 наблюдений над количественным признаком
наблюдений над количественным признаком 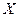 (выборка).
(выборка).
Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
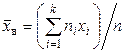 , (7.1)
, (7.1)
где  - варианта выборки,
- варианта выборки, 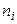 - частота варианты
- частота варианты  ,
, 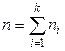 - объем выборки.
- объем выборки.
Замечание 1. Если первоначальные варианты  - большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число
- большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число 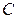 , т.е. перейти к условным вариантам
, т.е. перейти к условным вариантам  (в качестве
(в качестве 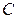 выгодно принять число, близкое к выборочной средней. Поскольку выборочная средняя неизвестна, число
выгодно принять число, близкое к выборочной средней. Поскольку выборочная средняя неизвестна, число 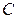 выбирают «на глаз»). Тогда
выбирают «на глаз»). Тогда
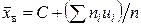 . (7.2)
. (7.2)
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
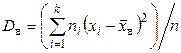 ; (7.3)
; (7.3)
эта оценка является смещенной, так как
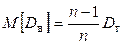 . (7.4)
. (7.4)
Более удобна формула
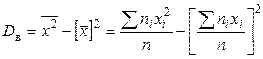 . (7.5)
. (7.5)
Замечание 2. Если первоначальные варианты  - большие числа, то целесообразно вычесть из всех вариант одно и то же число
- большие числа, то целесообразно вычесть из всех вариант одно и то же число 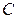 , равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам
, равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам  (дисперсия при этом не изменится). Тогда
(дисперсия при этом не изменится). Тогда
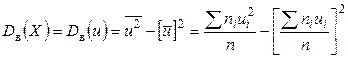 . (7.6)
. (7.6)
Замечание 3. Если первоначальные варианты являются десятичными дробями с  десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число
десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число  , т.е. переходят к условным вариантам
, т.е. переходят к условным вариантам 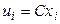 . При этом, дисперсия увеличивается в
. При этом, дисперсия увеличивается в 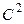 раз, поэтому, найдя дисперсию условных вариант, надо разделить ее на
раз, поэтому, найдя дисперсию условных вариант, надо разделить ее на 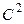 :
:
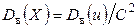 . (7.7)
. (7.7)
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
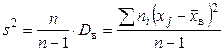 . (7.8)
. (7.8)
Более удобная формула
 . (7.9)
. (7.9)
В условных вариантах она имеет вид
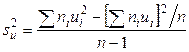 , (7.10)
, (7.10)
причем если  , то
, то 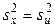 ; если
; если 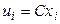 , то
, то 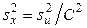 .
.
Замечание 4. При большом числе данных используют метод произведений или метод сумм.
Пример 7.1. Из генеральной совокупности извлечена выборка объема 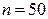 :
:
 .
.
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя
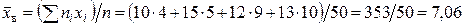 .
.
Пример 7.2. Найти выборочную среднюю по данному распределению выборки объема 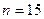 :
:
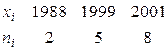 .
.
Решение. Первоначальные варианты – большие числа, поэтому перейдем к условным вариантам 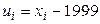 . В итоге получим распределение условных вариант:
. В итоге получим распределение условных вариант:
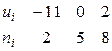 .
.
Найдем искомую выборочную среднюю:
 .
.
Пример 7.3. Найти выборочную дисперсию по данному распределению выборки объема 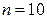 :
:
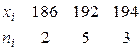 .
.
Решение. Варианты – сравнительно большие числа, поэтому перейдем к условным вариантам 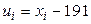 (мы вычли из вариант число
(мы вычли из вариант число 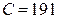 , близкое к выборочной средней). В итоге получим распределение условных вариант:
, близкое к выборочной средней). В итоге получим распределение условных вариант:
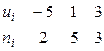 .
.
Найдем искомую выборочную дисперсию:

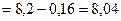 .
.
Метод моментов
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.
Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка:  . Учитывая, что
. Учитывая, что  и
и 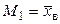 , получим
, получим
 . (8.1)
. (8.1)
Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (8.1) относительно неизвестного параметра, тем самым получим его точечную оценку.
Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:
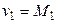 ,
,  .
.
Учитывая, что 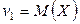 ,
, 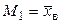 ,
,  ,
, 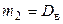 , имеем
, имеем
 (8.2)
(8.2)
Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (8.2) относительно неизвестных параметров, тем самым получим их точечные оценки.
Разумеется, для вычисления выборочной средней  и выборочной дисперсии
и выборочной дисперсии 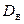 надо располагать выборкой
надо располагать выборкой 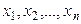 .
.
Пример 8.1. Случайная величина 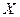 распределена по закону Пуассона
распределена по закону Пуассона
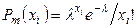 ,
,
где 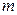 - число испытаний, произведенных в одном опыте;
- число испытаний, произведенных в одном опыте; 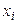 - число появлений события в
- число появлений события в 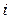 -м опыте.
-м опыте.
Найти методом моментов по выборке 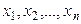 точечную оценку неизвестного параметра
точечную оценку неизвестного параметра 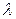 , определяющего распределение Пуассона.
, определяющего распределение Пуассона.
Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравняем начальный теоретический момент первого порядка 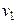 начальному эмпирическому моменту первого порядка
начальному эмпирическому моменту первого порядка 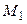 :
:
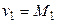 .
.
Приняв во внимание, что 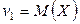 ,
, 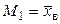 , получим
, получим 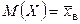 . Учитывая, что математическое ожидание распределения Пуассона равно параметру
. Учитывая, что математическое ожидание распределения Пуассона равно параметру 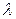 этого распределения, окончательно имеем
этого распределения, окончательно имеем 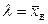 .
.
Итак, точечной оценкой параметра 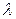 распределения Пуассона служит выборочная средняя:
распределения Пуассона служит выборочная средняя: 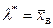 .
.
Пример 8.2. Найти методом моментов по выборке 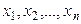 точечные оценки неизвестных параметров
точечные оценки неизвестных параметров  и
и 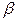 гамма-распределения, плотность которого
гамма-распределения, плотность которого
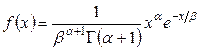
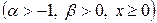 .
.
Решение. Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка 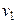 начальному эмпирическому моменту первого порядка
начальному эмпирическому моменту первого порядка 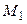 и центральный теоретический момент второго порядка
и центральный теоретический момент второго порядка 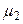 центральному эмпирическому моменту второго порядка
центральному эмпирическому моменту второго порядка 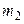 :
:
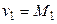 ,
,  .
.
Учитывая, что 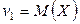 ,
, 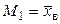 ,
,  ,
, 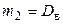 , имеем
, имеем
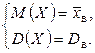 (8.3)
(8.3)
Математическое ожидание и дисперсия гамма-распределения соответственно равны  ,
,  , поэтому (8.3) можно записать в виде
, поэтому (8.3) можно записать в виде
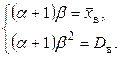
Решив эту систему, окончательно получим искомые точечные оценки неизвестных параметров: 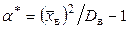 ,
, 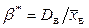 .
.
Интервальные оценки
Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью 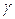 покрывает заданный параметр.
покрывает заданный параметр.
1. Интервальной оценкой (с надежностью 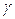 ) математического ожидания
) математического ожидания 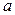 нормально распределенного количественного признака
нормально распределенного количественного признака 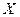 по выборочной средней
по выборочной средней 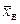 при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении 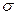 генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал
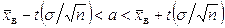 , (10.1)
, (10.1)
где 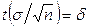 - точность оценки,
- точность оценки, 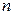 - объем выборки,
- объем выборки, 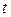 - значение аргумента функции Лапласа
- значение аргумента функции Лапласа 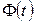 , при котором
, при котором 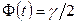 ; при неизвестном
; при неизвестном 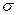 (и объеме выборки
(и объеме выборки 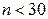 )
)
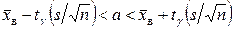 , (10.2)
, (10.2)
где 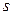 - «исправленное» выборочное среднее квадратическое отклонение,
- «исправленное» выборочное среднее квадратическое отклонение, 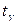 находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным 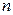 и
и 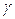 [3].
[3].
2. Интервальной оценкой (с надежностью 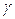 ) среднего квадратичекого отклонения
) среднего квадратичекого отклонения 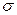 нормально распределенного количественного признака
нормально распределенного количественного признака 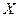 по «исправленному» выборочному среднему квадратическому отклонению
по «исправленному» выборочному среднему квадратическому отклонению 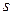 служит доверительный интервал
служит доверительный интервал
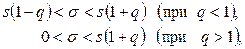 (10.3)
(10.3)
где 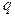 находят по таблице приложения 4 с заданными
находят по таблице приложения 4 с заданными 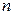 и
и 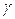 .
.
3. Интервальной оценкой (с надежностью 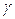 ) неизвестной вероятности
) неизвестной вероятности 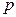 биноминального распределения по относительной частоте
биноминального распределения по относительной частоте 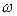 служит доверительный интервал (с приближенными концами
служит доверительный интервал (с приближенными концами 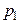 и
и 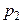 )
)
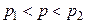 ,
,
где
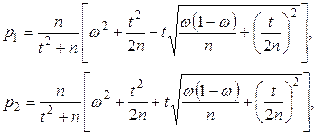 (10.4)
(10.4)
где 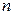 общее число испытаний;
общее число испытаний; 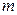 - число появлений события;
- число появлений события; 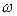 - относительная частота, равная отношению
- относительная частота, равная отношению 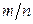 ;
; 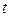 - значение аргумента функции Лапласа (приложение 2), при котором
- значение аргумента функции Лапласа (приложение 2), при котором 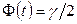 (
( 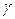 - заданная надежность).
- заданная надежность).
Замечание. При больших значениях 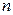 (порядка сотен) можно принять в качестве приближенных границ доверительного интервала
(порядка сотен) можно принять в качестве приближенных границ доверительного интервала
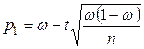 ,
, 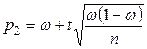 . (10.5)
. (10.5)
Пример 10.1. Найти доверительный интервал для оценки с надежностью 0,975 неизвестного математического ожидания 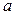 нормально распределенного признака
нормально распределенного признака 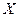 генеральной совокупности, если генеральное среднее квадратическое отклонение
генеральной совокупности, если генеральное среднее квадратическое отклонение 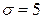 , выборочная средняя
, выборочная средняя 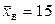 и объем выборки
и объем выборки 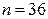 .
.
Решение. Требуется найти доверительный интервал
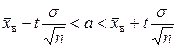 . (10.6)
. (10.6)
Все величины, кроме 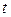 , известны. Найдем
, известны. Найдем 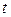 из соотношения
из соотношения 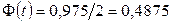 . По таблице приложения 1 находим
. По таблице приложения 1 находим 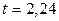 . Подставив
. Подставив 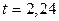 ,
, 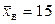 ,
, 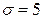 ,
, 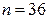 в (10.6), окончательно получим искомый доверительный интервал
в (10.6), окончательно получим искомый доверительный интервал 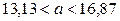 .
.
Пример 10.2. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожидания 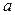 генеральной совокупности по выборочной средней равна
генеральной совокупности по выборочной средней равна 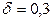 , если известно среднее квадратическое отклонение
, если известно среднее квадратическое отклонение 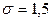 нормально распределенной генеральной совокупности.
нормально распределенной генеральной совокупности.
Решение. Воспользуемся формулой, определяющей точность оценки математического ожидания генеральной совокупности по выборочной средней: 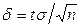 . Отсюда
. Отсюда
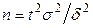 . (10.7)
. (10.7)
по условию, 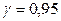 ; следовательно,
; следовательно, 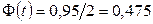 . По таблице приложения 2 найдем
. По таблице приложения 2 найдем 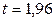 . Подставив
. Подставив 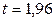 ,
, 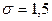 и
и 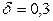 в (10.7), получим искомый объем выборки
в (10.7), получим искомый объем выборки 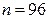 .
.
Пример 10.3. Произведено 15 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем «исправленное» среднее квадратическое отклонение 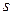 случайных ошибок измерений оказалось равным 0,7. Найти точность прибора с надежностью 0,99. Предполагается, что результаты измерений распределены нормально.
случайных ошибок измерений оказалось равным 0,7. Найти точность прибора с надежностью 0,99. Предполагается, что результаты измерений распределены нормально.
Решение. Точность прибора характеризуется средним квадратическом отклонением случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала, покрывающего 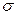 с заданной надежностью
с заданной надежностью 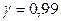 :
:
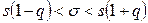 . (10.8)
. (10.8)
По данным 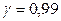 и
и 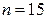 по таблице приложения 4 найдем
по таблице приложения 4 найдем 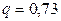 . Подставив
. Подставив 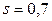 ,
, 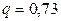 в соотношение (10.8), окончательно получим
в соотношение (10.8), окончательно получим 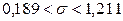 .
.
Средней и дисперсии
11.1. Равноотстоящие варианты
Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае удобно находить выборочную среднюю и дисперсию методом произведений по формулам
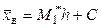 ,
, 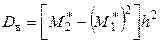 ,
,
где 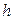 - шаг (разность между двумя соседними вариантами);
- шаг (разность между двумя соседними вариантами); 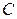 - ложный нуль (варианта, которая расположена примерно в середине вариационного ряда);
- ложный нуль (варианта, которая расположена примерно в середине вариационного ряда); 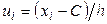 - условная варианта;
- условная варианта; 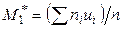 - условный момент первого порядка;
- условный момент первого порядка; 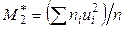 - условный момент второго порядка.
- условный момент второго порядка.
Пример 11.1. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема 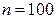 :
:
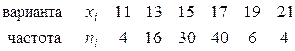 .
.
Решение. Составим расчетную табл. 11.1; для этого:
1) запишем варианты в первый столбец;
2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;
3) в качестве ложного нуля 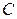 выберем варианту (17), которая имеет наибольшую частоту (в качестве
выберем варианту (17), которая имеет наибольшую частоту (в качестве 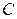 можно взять любую варианту, расположенную примерно в середине столбца); в клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0; над нулем последовательно записываем -1, -2, -3 а под нулем 1, 2;
можно взять любую варианту, расположенную примерно в середине столбца); в клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0; над нулем последовательно записываем -1, -2, -3 а под нулем 1, 2;
4) произведения частот 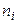 на условные варианты
на условные варианты 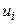 запишем в четвертый столбец; отдельно находим сумму (А1=--74) отрицательных чисел и отдельно сумму (А2=14) положительных чисел; сложив эти числа, их сумму (-60) помещаем в нижнюю клетку четвертого столбца;
запишем в четвертый столбец; отдельно находим сумму (А1=--74) отрицательных чисел и отдельно сумму (А2=14) положительных чисел; сложив эти числа, их сумму (-60) помещаем в нижнюю клетку четвертого столбца;
5) произведения частот на квадраты условных вариант, т.е. 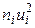 , запишем в пятый столбец (удобнее перемножить числа каждой строки третьего и четвертого столбцов;
, запишем в пятый столбец (удобнее перемножить числа каждой строки третьего и четвертого столбцов; 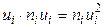 ); сумму чисел столбца (152) помещаем в нижнюю клетку пятого столбца;
); сумму чисел столбца (152) помещаем в нижнюю клетку пятого столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, т.е. 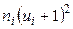 , запишем в шестой контрольный столбец; сумму чисел столбца (132) помещаем в нижнюю клетку шестого столбца.
, запишем в шестой контрольный столбец; сумму чисел столбца (132) помещаем в нижнюю клетку шестого столбца.
В итоге получим расчетную табл. 11.1.
Для контроля вычислений пользуются тождеством
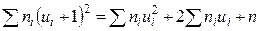 .
.
Контроль:
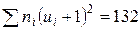 ,
, 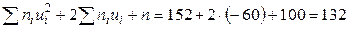 .
.
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков:
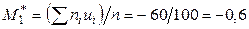 ;
; 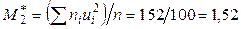 .
.
Найдем шаг (разность между любыми двумя соседними вариантами): 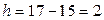 .
.
Вычислим искомые выборочные среднюю и дисперсию, учитывая, что ложный нуль (варианта, которая имеет наибольшую частоту) 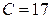 :
:
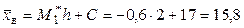 ;
;
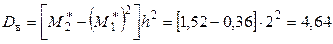 .
.
Таблица 11.1
| 1 | 2 | 3 | 4 | 5 | 6 |
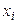
| 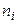
| 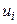
| 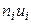
| 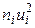
| 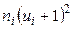
|
| 11 | 4 | -3 | -12 | 36 | 16 |
| 13 | 16 | -2 | -32 | 64 | 16 |
| 15 | 30 | -1 | -30 | 30 | 0 |
| 17 | 40 | 0 | А1=-74 | 40 | |
| 19 | 6 | 1 | 6 | 6 | 24 |
| 21 | 4 | 2 | 8 | 16 | 36 |
| А2=14 | |||||
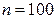
| 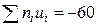
| 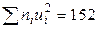
| 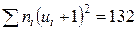
|
11.2. Неравноотстоящие варианты
Если первоначальные варианты не являются равноотстоящими, то интервал, в котором заключены все варианты выборки, делят на несколько равных, длины 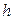 , частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.
, частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.
При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой (особенно при малом числе интервалов), делают поправку Шеппарда, а именно вычитают из вычисленной дисперсии 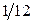 квадрата длины частичного интервала.
квадрата длины частичного интервала.
Таким образом, с учетом поправки Шеппарда дисперсию вычисляют по формуле
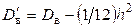 .
.
Пример 11.2. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема 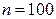 :
:
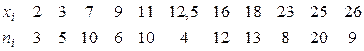 .
.
Решение. Разобьем интервал 2-26 на следующие четыре частичных интервала длины  .приняв середины частичных интервалов в качестве новых вариант
.приняв середины частичных интервалов в качестве новых вариант 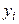 , получим равноотстоящие варианты:
, получим равноотстоящие варианты: 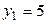 ,
, 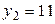 ,
, 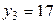 ,
, 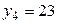 .
.
В качестве частоты 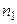 варианты
варианты 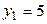 примем сумму частот вариант, попавших в первый интервал:
примем сумму частот вариант, попавших в первый интервал: 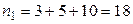 .
.
Вычислим аналогично частоты остальных вариант, получим распределение равноотстоящих вариант:
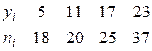
Пользуясь методом произведений, найдем 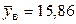 ,
, 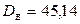 .
.
Принимая во внимание, что число частичных интервалов (4) мало, учтем поправку Шеппарда:
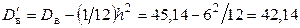 .
.
Интервал конфиденции
Лишь в редких случаях можно довольствоваться тем, что найдена некоторая оценка неизвестного параметра: обычно находится определитель, насколько данная оценка является точной, иными словами следует найти такой интервал, содержащий неизвестный параметр с большой вероятностью. Такой интервал называется интервалом конфиденции.
Метод определения интервала конфиденции можно показать на следующем примере. Пусть 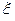 представляет собой случайную переменную с нормальным распределением, с известной дисперсией
представляет собой случайную переменную с нормальным распределением, с известной дисперсией 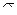 и с неизвестным значением математического ожидания
и с неизвестным значением математического ожидания 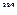 . Пусть
. Пусть 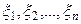 представляют собой такую пробу, из которой следует определить интервал конфиденции. Как известно, значение математического ожидания
представляют собой такую пробу, из которой следует определить интервал конфиденции. Как известно, значение математического ожидания 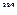 оценивается с помощью статистики [1]
оценивается с помощью статистики [1]
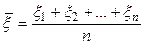 ,
,
поэтому естественно искать интервал конфиденции в виде 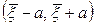 . Точнее задача заключается в таком определении значения
. Точнее задача заключается в таком определении значения 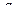 , чтобы интервал
, чтобы интервал 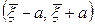 содержал в себе неизвестный параметр
содержал в себе неизвестный параметр 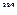 с большой вероятностью. Нетрудно увидеть, что
с большой вероятностью. Нетрудно увидеть, что
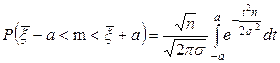 .
.
Таким образом, с помощью таблицы, представленной для функции 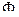 , может быть определено значение
, может быть определено значение 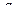 при условии, что интервал
при условии, что интервал 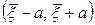 содержит в себе значение
содержит в себе значение 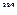 с желаемой вероятностью.
с желаемой вероятностью.
Теория игр
Основателем теории игр считают математика Иоганна фон Неймана. Им доказаны основная теорема теории игр и возможности ее практического применения.
В теории игр речь идет об играх двух лиц. Предполагается, что игры являются ограниченными, т.е. оба игрока в обоих случаях могут делать только определенное количество шагов и игра заканчивается после ограниченного количества шагов. Отсюда вытекает ограниченность числа стратегий обоих игроков.
Под понятием стратегии подразумевается такая система правил, с помощью которой задается, как ходит игрок в некоторой данной ситуации.
В игре бывают и случайные ходы (например, подбрасывание игральной кости, раздача карт и т.д.). Таким образом, даже знанием стратегий обоих игроков не определяется однозначно исход игры. Пусть 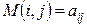 означает значение математического ожидания выигрыша первого игрока при условии, что первый игрок проводит игру по
означает значение математического ожидания выигрыша первого игрока при условии, что первый игрок проводит игру по 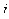 -той, а второй – по
-той, а второй – по 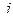 -той стратегии. В соответствии с этим вся игра может рассматриваться с помощью матрицы размерности
-той стратегии. В соответствии с этим вся игра может рассматриваться с помощью матрицы размерности 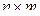 , где
, где  - означает число стратегий первого, а
- означает число стратегий первого, а 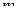 - второго игрока. Элемент матрицы
- второго игрока. Элемент матрицы 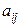 в
в 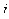 -той строке и в
-той строке и в 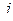 -том столбце представляет собой значение математического ожидания первого игрока. Такая игра иногда называется матричной игрой.
-том столбце представляет собой значение математического ожидания первого игрока. Такая игра иногда называется матричной игрой.
Стратегия. Целью теории игр (обычно в матричных играх) является нахождение лучшей стратегии отдельных игроков. В большинстве игр было бы целесообразно применять всегда одну и ту же стратегию, так как если противник определит нашу стратегию, ему легче будет найти хорошую обратную стратегию. Таким образом, кажется вероятным получение лучшей стратегии в том случае, когда стратегия выбирается случайным образом из отдельных стратегий. Предположим, что первый игрок выбирает свою стратегию из возможных с вероятностью 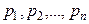
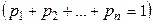 , а второй – с вероятностью
, а второй – с вероятностью 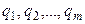
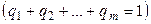 , соответственно. В таком случае математическое ожидание выигрыша отдельных игроков определяется выражением:
, соответственно. В таком случае математическое ожидание выигрыша отдельных игроков определяется выражением:
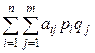 . (15.1)
. (15.1)
Цена игр. Первый игрок может проводить следующее рассуждение: если я выбираю свои стратегии с вероятностями 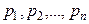 , то могу предположить, что мой противник будет выбирать свои с вероятностями
, то могу предположить, что мой противник будет выбирать свои с вероятностями 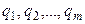 , при которых математическое ожидание моего выигрыша будет очень мало. Иначе говоря, если я буду выбирать из моих стратегий по распределению вероятностей
, при которых математическое ожидание моего выигрыша будет очень мало. Иначе говоря, если я буду выбирать из моих стратегий по распределению вероятностей 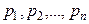 , то математическое ожидание моего выигрыша будет, по меньшей мере,
, то математическое ожидание моего выигрыша будет, по меньшей мере,
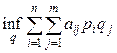 , (15.2)
, (15.2)
где инфимум относится ко всем распределениям вероятностей 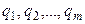 . Итак, лучшим можно считать такое распределение вероятностей
. Итак, лучшим можно считать такое распределение вероятностей 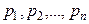 , для которого самое большое возможное значение имеет выражение (15.2).
, для которого самое большое возможное значение имеет выражение (15.2).
Аналогично, для второго игрока лучшей стратегией является выбор по распределению вероятностей 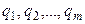 , для которого значение выражения
, для которого значение выражения
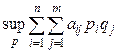 (15.3)
(15.3)
имеет наименьшее возможное значение.
По основной теореме теории игр выполняется следующее соотношение:
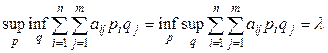 . (15.4)
. (15.4)
Данное число называется ценой игры.
Итак, по основной теореме теории игр утверждается, что первый игрок имеет такую стратегию, при использовании которой математическое ожидание его выигрыша будет по меньшей мере 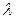 (при выборе вторым игроком любой стратегии); а второй игрок имеет такую стратегию, при которой математическое ожидание его потери будет по крайней мере
(при выборе вторым игроком любой стратегии); а второй игрок имеет такую стратегию, при которой математическое ожидание его потери будет по крайней мере 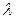 .
.
Решающие функции
Теория решающих функций является одной из наиболее новых областей статистики. Хотя они применяются широко, решающие функции здесь представлены только на примере контроля качества товара. Очевидно, что в некотором объеме товара процент брака оценивается тем точнее, чем больше элементов выбирается для пробы. Снятие пробы со многими элементами, однако, может быть связано с большими расходами. Может быть дорогостоящим и исследование элементов пробы, и бывает, когда в результате исследования элементы придут в негодное состояние. (Если, например, исследуется срок перегорания электрических ламп, приходится прокалить несколько электрических ламп).
Так как снятие проб связано с расходами, статистику нужно стремиться принять решение на основе пробы с небольшим количеством элементов. Однако решение, принятое на основе пробы с небольшим количеством элементов, будет ошибочно с большей вероятностью, чем решение, принятое на основе пробы с большим количеством элементов. Ошибочное решение может привести к крупным потерям. Статистик должен выбрать такое число элементов пробы, при котором расходы (расходы снятия пробы плюс расходы из-за ошибочных решений) будут минимальными.
Пусть 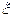 - некоторая случайная переменная с неизвестной
- некоторая случайная переменная с неизвестной 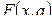 функцией распределения, с неизвестным параметром
функцией распределения, с неизвестным параметром 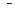 . Например,
. Например, 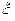 может означать некоторую характеристику поставляемого товара (например, вес, длину), и параметр
может означать некоторую характеристику поставляемого товара (например, вес, длину), и параметр 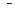 , например, может представлять математическое ожидание случайной величины
, например, может представлять математическое ожидание случайной величины 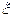 .
.
Решение следует принимать на основе пробы с  элементами
элементами 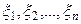 . Предположим, что возможные решения могут быть
. Предположим, что возможные решения могут быть 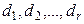 . Решение принимается на основе исследования пробы
. Решение принимается на основе исследования пробы 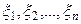 , т.е. дается объяснение
, т.е. дается объяснение  -мерной решающей функции
-мерной решающей функции 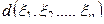 , возможными значениями которой являются возможные решения
, возможными значениями которой являются возможные решения 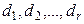 .
.
Пусть обозначаются суммарные расходы через 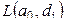 , если предположить, что значением параметра
, если предположить, что значением параметра 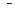 является
является 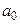 и в результате исследования пробы
и в результате исследования пробы 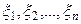 принято решение
принято решение 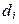 . Зная функции
. Зная функции 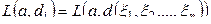 и
и 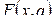 (функция распределения), математическое ожидание расходов станет исчислимым при условии
(функция распределения), математическое ожидание расходов станет исчислимым при условии 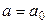 . Пусть такое математическое ожидание обозначается через
. Пусть такое математическое ожидание обозначается через
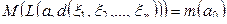 .
.
Количество элементов пробы  и решающую функцию
и решающую функцию 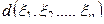 следует выбирать таким образом, чтобы значение
следует выбирать таким образом, чтобы значение 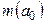 было по возможности мало при любом значении
было по возможности мало при любом значении 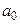 , или иными словами, ищутся такое значение
, или иными словами, ищутся такое значение  и такая функция
и такая функция 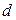 , для которых значение
, для которых значение 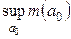 является минимальным.
является минимальным.
Такой вывод делается на основе рассуждений, проводимых по теории игр. Представим себе, что статистик и «природа» играют; в этой игре природа имеет право выбирать значение параметра 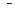 , а правом статистика является выбирать решающую функцию. Иначе говоря, стратегиями природы являются возможные значения параметра
, а правом статистика является выбирать решающую функцию. Иначе говоря, стратегиями природы являются возможные значения параметра 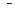 , а стратегиями статистика – возможные решения. (Такая игра обычно не является конечной). По рассуждениям, проводимым в соответствии с теорией игр, очевидно, что самая хорошая стратегия статистика будет такая, что он случайно выбирает решение из возможных решений с некоторым распределением вероятностей.
, а стратегиями статистика – возможные решения. (Такая игра обычно не является конечной). По рассуждениям, проводимым в соответствии с теорией игр, очевидно, что самая хорошая стратегия статистика будет такая, что он случайно выбирает решение из возможных решений с некоторым распределением вероятностей.
Другой результат будет получен, если параметр 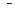 рассматривается как случайная переменная. Тогда ситуация рассматривается таким образом, что значение
рассматривается как случайная переменная. Тогда ситуация рассматривается таким образом, что значение 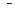 является числом, зависящим от различных случайных факторов в некотором объеме товара, доставляемого в разных случаях. Предположим, что известна функция распределения
является числом, зависящим от различных случайных факторов в некотором объеме товара, доставляемого в разных случаях. Предположим, что известна функция распределения 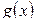 случайной переменной
случайной переменной 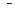 , тогда величина
, тогда величина 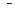 также представляет собой случайную переменную. В таком случае статистический метод целесообразно выбирать таким образом, чтобы значение математического ожидания
также представляет собой случайную переменную. В таком случае статистический метод целесообразно выбирать таким образом, чтобы значение математического ожидания 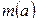 было минимальным.
было минимальным.
З адача математической статистики
В теории вероятностей обычно исходят из того, что известны или вероятность некоторых более простых событий, или функции распределения некоторых случайных переменных. При подбрасывании монеты, например, нам известно (как предварительное условие), что подбрасываемая монета имеет симметричную форму. Но это не доказано нами. Может возникнуть вопрос: «Имеет ли подбрасываемая монета действительно симметричную форму?». Симметричность монеты может быть проверена применением некоторого физического метода. Если данная монета подбрасывается много раз подряд и орел выпадает примерно в половине всех экспериментов, то можно предположить, что монета является симметричной. Чтобы высказать такое предположение, необходимо определить, что подразумевается под термином «монета подбрасывается много раз» и «примерно в половине». С помощью математической статистики можно ответить на эти вопросы, так как ее задачей является определение на основе результатов экспериментов вероятности некоторых событий, функции плотности случайных переменных, математического ожидания, дисперсии и других характерных черт. Но бывает (небольшая вероятность), что монета выпадет на орел много раз подряд; в таком случае принимается решение: монета не имеет симметричную форму. Но может случиться, что монета несимметричной формы выпадает на орел именно в половине первой части экспериментов и в этом случае также принимается ошибочное решение. На основе применения методов математической статистики можно утверждать о правильности решения с большой вероятностью.
Исследование гипотез
Часто приходится отвечать на вопрос о правильности или неправильности некоторой гипотезы. Например, если на каком-то заводе приняли определенную партию товара, то не обязательно знать точно, сколько процентов составляют бракованные предметы в партии товара. Обычно достаточно определить, что относительное количество бракованного товара больше или меньше чем 3%. В первом случае партия товара будет отвергнута, а во втором – принята. Для реализации исследований статистических гипотез служат статистические пробы.
Проба 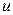 . Пусть
. Пусть 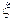 представляет собой случайную переменную с нормальным распределением, с известной дисперсией
представляет собой случайную переменную с нормальным распределением, с известной дисперсией 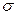 . Надо проверить такую гипотезу, равняется ли математическое ожидание случайной величины
. Надо проверить такую гипотезу, равняется ли математическое ожидание случайной величины 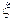 определенному числу
определенному числу 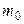 .
.
Для контроля данной гипотезы выбирается проба из 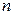 элементов таким образом, что элементы пробы выбираются независимо друг от друга. Пусть результатом снятий проб будут величины
элементов таким образом, что элементы пробы выбираются независимо друг от друга. Пусть результатом снятий проб будут величины 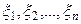 . Проведем расчет величины
. Проведем расчет величины
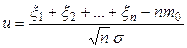 . (2.1)
. (2.1)
Можно увидеть, что случайная переменная 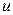 имеет нормальное распределение, дисперсию 1; если выполняется гипотеза
имеет нормальное распределение, дисперсию 1; если выполняется гипотеза 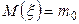 , то
, то 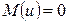 . Таким образом, при выполнении данной гипотезы действительно следующее соотношение:
. Таким образом, при выполнении данной гипотезы действительно следующее соотношение:
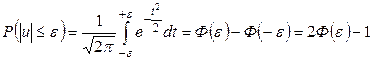 . (2.2)
. (2.2)
Пусть 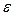 будет таким, что можно было выполнить соотношение
будет таким, что можно было выполнить соотношение
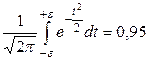 . (2.3)
. (2.3)
В таком случае, если из пробы получено такое значение 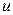 , абсолютная величина которого больше чем
, абсолютная величина которого больше чем 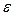 , то гипотеза
, то гипотеза 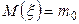 может быть отвергнута, так как произошло событие, которое является невероятным при правильности гипотезы. Иными словами, если гипотеза
может быть отвергнута, так как произошло событие, которое является невероятным при правильности гипотезы. Иными словами, если гипотеза 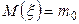 отвергнута при выполнении условия
отвергнута при выполнении условия 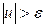 , то только в 5% всех случаев будет отвергнута правильная гипотеза.
, то только в 5% всех случаев будет отвергнута правильная гипотеза.
Бывает и так, что гипотеза 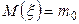 не выполняется и все-таки принимается решение о правильности гипотезы. Вероятность ошибки такого рода нельзя определить так просто, как в случае проявления ошибки другого характера. Ибо в этом случае, если
не выполняется и все-таки принимается решение о правильности гипотезы. Вероятность ошибки такого рода нельзя определить так просто, как в случае проявления ошибки другого характера. Ибо в этом случае, если 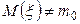 , все равно
, все равно 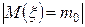 представляет собой малую величину. В таком случае более вероятно, что мы примем неправильную гипотезу
представляет собой малую величину. В таком случае более вероятно, что мы примем неправильную гипотезу 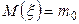 , чем в том случае, когда
, чем в том случае, когда 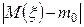 имеет очень большое значение. В случае, если
имеет очень большое значение. В случае, если 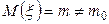 , гипотеза принимается с вероятностью
, гипотеза принимается с вероятностью
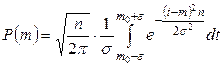 . (2.4)
. (2.4)
Данная формула показывает, что если значение 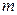 близко к значению
близко к значению 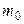 , то с вероятностью
, то с вероятностью 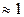 принимается гипотеза
принимается гипотеза 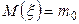 ; если значение
; если значение 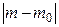 велико, то гипотеза отвергается с вероятностью
велико, то гипотеза отвергается с вероятностью 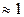 .
.
Функция 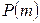 называется силовой функцией пробы.
называется силовой функцией пробы.
Проба 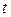 . При использовании пробы
. При использовании пробы 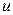 незнание дисперсии обычно представляет собой серьезное затруднение. Пусть
незнание дисперсии обычно представляет собой серьезное затруднение. Пусть 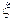 означает случайную переменную с нормальным распределением. Проверяется гипотеза о том, равняется ли математическое ожидание случайной переменной
означает случайную переменную с нормальным распределением. Проверяется гипотеза о том, равняется ли математическое ожидание случайной переменной 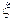 определенному числу
определенному числу 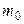 . Проведем
. Проведем 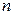 экспериментов, результаты которых обозначим знаками
экспериментов, результаты которых обозначим знаками 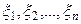 . Оценивается значение выражения
. Оценивается значение выражения
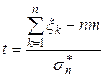 , (2.5)
, (2.5)
где
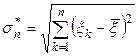 (2.6)
(2.6)
и
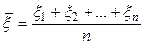 . (2.7)
. (2.7)
Функция распределения случайной переменной 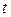 оценивается просто и ее значения могут быть собраны в таблицах. Имея таблицы, можно решить вопрос о правильности гипотезы
оценивается просто и ее значения могут быть собраны в таблицах. Имея таблицы, можно решить вопрос о правильности гипотезы 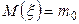 , как это было показано при представлении пробы
, как это было показано при представлении пробы 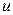 .
.
При применении подобных проб можно решить вопрос о принятии или отклонении других статических гипотез. Ниже приведены только некоторые виды гипотез, для которых уже разработаны пробы.
Часто бывают такие случаи, когда необходимо знать закон распределения случайной переменной, а иногда закон распределения известен, но неизвестны его параметры. В таких случаях выдвигают гипотезу либо о законе распределения, либо гипотезу, связанную с параметрами закона распределения.
Наряду с выдвинутой гипотезой, рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.
Выдвинутую гипотезу называют нулевой (основной).
Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой.
Различают гипотезы, которые содержат только одно и более одного предположений.
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.
Статистическим критерием (или просто критерием) называют случайную величину, которая служит для проверки нулевой гипотезы.
Наблюдаемым значением называют значение критерия, вычисленное по выборкам.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (область допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Поскольку критерий – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.
В приложениях 5-9 приведены значения критических точек распределения 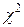 , Стьюдента, Фишера-Снедекора, Кохрена [4].
, Стьюдента, Фишера-Снедекора, Кохрена [4].
Дата: 2019-03-05, просмотров: 383.