Асимметрия и эксцесс эмпирического распределения определяются, соответственно, равенствами:
, 
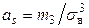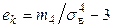; (13.1)
здесь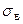 
- выборочное среднее квадратическое отклонение; 
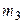и 
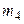- центральные эмпирические моменты третьего и четвертого порядков:
, 
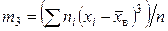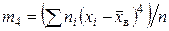. (13.2)
Эти моменты в случае равноотстоящих вариант с шагом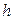 
(шаг равен разности между любыми двумя соседними вариантами) удобно вычислять по формулам:
,
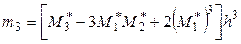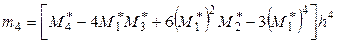, (13.3)
где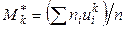 
- условные моменты 
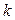-го порядка 
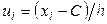- условные варианты. Здесь 
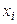- первоначальные варианты; 
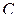- ложный нуль, т.е. варианта, имеющая наибольшую частоту (либо любая варианта, расположенная примерно в середине вариационного ряда).
Итак, для отыскания асимметрии и эксцесса необходимо вычислить условные моменты, что можно сделать методом произведений или методом сумм.
13.1. Метод произведений
Пример 13.1.1. Найти метод произведений асимметрию и эксцесс по заданному распределению выборки объема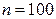 
:
.
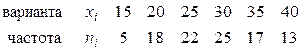Решение. Воспользуемся методом произведений. Составим расчетную табл. 13.1. В §11 при решении примера 1 уже было указано, как заполняются столбцы 1-5 расчетной таблицы, поэтому ограничимся краткими пояснениями.
Для заполнения столбца 6 удобно перемножить числа каждой строки столбцов 3 и 5. Для заполнения столбца 7 удобно перемножать числа каждой строки столбцов 3 и 6. Столбец 8 служит для контроля вычислений с помощью тождества:
.
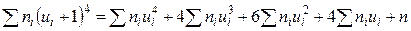Приведем расчетную табл. 13.1.
Таблица 13.1.1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
| 
| 
| 
| 
| 
| 
| 
|
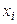
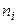
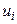
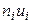
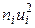
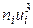
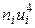
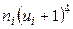
| 15 | 5 | -3 | -15 | 45 | -135 | 405 | 80 |
| 20 | 18 | -2 | -36 | 72 | -144 | 288 | 18 |
| 25 | 22 | -1 | -22 | 22 | -22 | 22 | 0 |
| 30 | 25 | 0 | 0 | 0 | 0 | 0 | 25 |
| 35 | 17 | 1 | 17 | 17 | 17 | 17 | 272 |
| 40 | 13 | 2 | 26 | 52 | 104 | 208 | 1053 |
|
| 
| 
| 
| 
| 
|
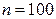
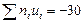
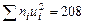
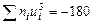
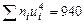
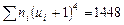
Контроль:
,
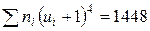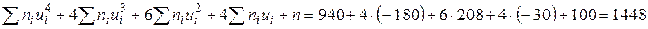
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Найдем условные моменты третьего и четвертого порядков (условные моменты первого и второго порядков вычислены в примере 1: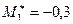 
; 
):
; 
.
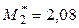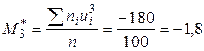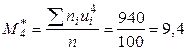Найдем центральные эмпирические моменты третьего и четвертого порядков:
,
.
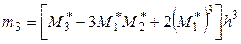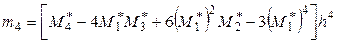Подставляя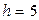 
и 
, 
, 
, 
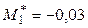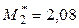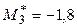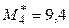, получим 
, 
.
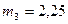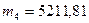Найдем искомые асимметрию и эксцесс, учитывая, что
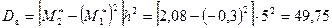и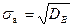 
:
;
.
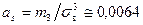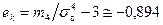13.2. Метод сумм
Пример 13.2.1. Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема :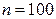
.
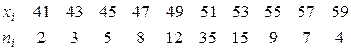Решение. Воспользуемся методом сумм, для этого составим расчетную табл. 13.2. В §12 уже было указано, как заполняются столбцы 1-4 расчетной таблицы, поэтому ограничимся краткими пояснениями.
Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (51); над этим нулем и под ним поставим еще по два нуля.
В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты: 2; 2+8=10; 2+8+20=30. Сложив накопленные частоты, получим число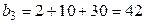 
, которое поместим в верхнюю клетку пятого столбца.
В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вверх; в итоге будем иметь следующие накопленные частоты: 5; 5+17=22. Сложив накопленные частоты, получим число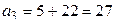 
, которое поместим в нижнюю клетку пятого столбца.
Аналогично заполняют столбец 6, причем суммируем частоты столбца 5. Сложив накопленные частоты, расположенные над нулями, получим число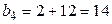 
, которое запишем в верхнюю клетку шестого столбца. Сложив числа, расположенные под нулями (в нашей задаче есть лишь одно слагаемое), получим число 
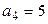, которое поместим в нижнюю клетку шестого столбца.
В итоге получим расчетную табл. 13.2.
Контроль: сумма чисел, расположенных непосредственно над нулем третьего столбца, слева от него и под ним, должна быть равна объему выборки (30+35+35=100); сумма двух чисел, расположенных над двумя ступеньками ступенчатой линии (обведены жирными отрезками), должна быть рана соответственно числам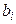 
, стоящими над предшествующей ступенькой (при движении по «лесенке» вверх): 
; 
; 
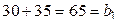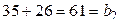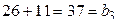. Аналогично проверяется совпадение сумм двух чисел, стоящих под «ступеньками лесенки», ведущей вниз: 
; 
; 
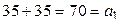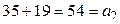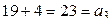. При несовпадении хотя бы одной из указанных сумм следует искать ошибку в расчете.
Таблица 13.2.1
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 
| 
| 
| 
| 
|
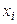
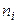
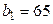
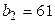
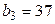
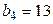
| 41 | 2 | 2 | 2 | 2 | 2 |
| 43 | 3 | 5 | 7 | 9 | 11 |
| 45 | 5 | 10 | 17 | 26 | 0 |
| 47 | 8 | 18 | 35 | 0 | 0 |
| 49 | 12 | 30 | 0 | 0 | 0 |
| 51 | 35 | 0 | 0 | 0 | 0 |
| 53 | 15 | 35 | 0 | 0 | 0 |
| 55 | 9 | 20 | 35 | 0 | 0 |
| 57 | 7 | 11 | 15 | 19 | 0 |
| 59 | 4 | 4 | 4 | 4 | 4 |
| 
| 
| 
| 
|
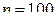
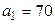
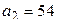
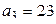
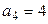
Найдем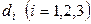 
и 
:
, 
, 
;
; 
;
; 
.
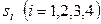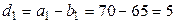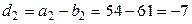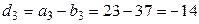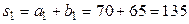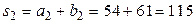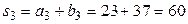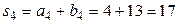Найдем условные моменты первого, второго, третьего и четвертого порядков:
; 
;
;
.
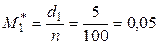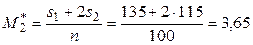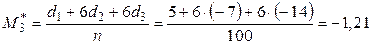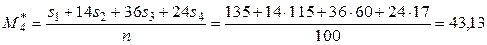Найдем центральные эмпирические моменты третьего и четвертого порядков:
,
.
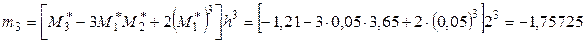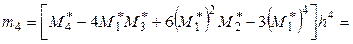
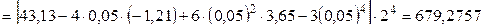Найдем искомые асимметрию и эксцесс, учитывая, что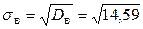 
( 
):
;
.
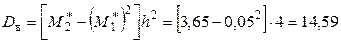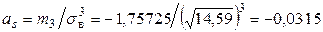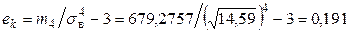Интервал конфиденции
Лишь в редких случаях можно довольствоваться тем, что найдена некоторая оценка неизвестного параметра: обычно находится определитель, насколько данная оценка является точной, иными словами следует найти такой интервал, содержащий неизвестный параметр с большой вероятностью. Такой интервал называется интервалом конфиденции.
Метод определения интервала конфиденции можно показать на следующем примере. Пусть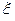 
представляет собой случайную переменную с нормальным распределением, с известной дисперсией 
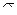и с неизвестным значением математического ожидания 
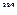. Пусть 
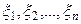представляют собой такую пробу, из которой следует определить интервал конфиденции. Как известно, значение математического ожидания 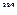оценивается с помощью статистики [1]
,
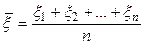поэтому естественно искать интервал конфиденции в виде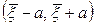 
. Точнее задача заключается в таком определении значения 
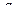, чтобы интервал 
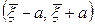содержал в себе неизвестный параметр 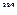с большой вероятностью. Нетрудно увидеть, что
.
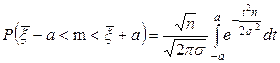Таким образом, с помощью таблицы, представленной для функции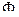 
, может быть определено значение 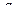при условии, что интервал 
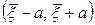содержит в себе значение 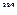с желаемой вероятностью.
Теория игр
Основателем теории игр считают математика Иоганна фон Неймана. Им доказаны основная теорема теории игр и возможности ее практического применения.
В теории игр речь идет об играх двух лиц. Предполагается, что игры являются ограниченными, т.е. оба игрока в обоих случаях могут делать только определенное количество шагов и игра заканчивается после ограниченного количества шагов. Отсюда вытекает ограниченность числа стратегий обоих игроков.
Под понятием стратегии подразумевается такая система правил, с помощью которой задается, как ходит игрок в некоторой данной ситуации.
В игре бывают и случайные ходы (например, подбрасывание игральной кости, раздача карт и т.д.). Таким образом, даже знанием стратегий обоих игроков не определяется однозначно исход игры. Пусть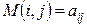 
означает значение математического ожидания выигрыша первого игрока при условии, что первый игрок проводит игру по 
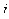-той, а второй – по 
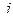-той стратегии. В соответствии с этим вся игра может рассматриваться с помощью матрицы размерности 
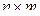, где 
- означает число стратегий первого, а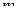 
- второго игрока. Элемент матрицы 
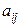в 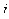-той строке и в 
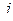-том столбце представляет собой значение математического ожидания первого игрока. Такая игра иногда называется матричной игрой.
Стратегия. Целью теории игр (обычно в матричных играх) является нахождение лучшей стратегии отдельных игроков. В большинстве игр было бы целесообразно применять всегда одну и ту же стратегию, так как если противник определит нашу стратегию, ему легче будет найти хорошую обратную стратегию. Таким образом, кажется вероятным получение лучшей стратегии в том случае, когда стратегия выбирается случайным образом из отдельных стратегий. Предположим, что первый игрок выбирает свою стратегию из возможных с вероятностью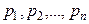 
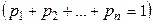, а второй – с вероятностью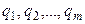 
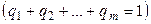, соответственно. В таком случае математическое ожидание выигрыша отдельных игроков определяется выражением:
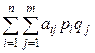. (15.1)
Цена игр. Первый игрок может проводить следующее рассуждение: если я выбираю свои стратегии с вероятностями 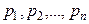, то могу предположить, что мой противник будет выбирать свои с вероятностями 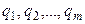, при которых математическое ожидание моего выигрыша будет очень мало. Иначе говоря, если я буду выбирать из моих стратегий по распределению вероятностей 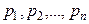, то математическое ожидание моего выигрыша будет, по меньшей мере,
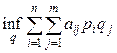, (15.2)
где инфимум относится ко всем распределениям вероятностей 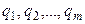. Итак, лучшим можно считать такое распределение вероятностей 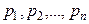, для которого самое большое возможное значение имеет выражение (15.2).
Аналогично, для второго игрока лучшей стратегией является выбор по распределению вероятностей 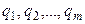, для которого значение выражения
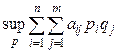(15.3)
имеет наименьшее возможное значение.
По основной теореме теории игр выполняется следующее соотношение:
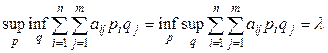. (15.4)
Данное число называется ценой игры.
Итак, по основной теореме теории игр утверждается, что первый игрок имеет такую стратегию, при использовании которой математическое ожидание его выигрыша будет по меньшей мере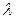 
(при выборе вторым игроком любой стратегии); а второй игрок имеет такую стратегию, при которой математическое ожидание его потери будет по крайней мере .
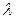Решающие функции
Теория решающих функций является одной из наиболее новых областей статистики. Хотя они применяются широко, решающие функции здесь представлены только на примере контроля качества товара. Очевидно, что в некотором объеме товара процент брака оценивается тем точнее, чем больше элементов выбирается для пробы. Снятие пробы со многими элементами, однако, может быть связано с большими расходами. Может быть дорогостоящим и исследование элементов пробы, и бывает, когда в результате исследования элементы придут в негодное состояние. (Если, например, исследуется срок перегорания электрических ламп, приходится прокалить несколько электрических ламп).
Так как снятие проб связано с расходами, статистику нужно стремиться принять решение на основе пробы с небольшим количеством элементов. Однако решение, принятое на основе пробы с небольшим количеством элементов, будет ошибочно с большей вероятностью, чем решение, принятое на основе пробы с большим количеством элементов. Ошибочное решение может привести к крупным потерям. Статистик должен выбрать такое число элементов пробы, при котором расходы (расходы снятия пробы плюс расходы из-за ошибочных решений) будут минимальными.
Пусть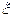 
- некоторая случайная переменная с неизвестной 
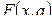функцией распределения, с неизвестным параметром 
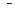. Например, 
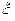может означать некоторую характеристику поставляемого товара (например, вес, длину), и параметр 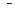, например, может представлять математическое ожидание случайной величины .
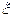Решение следует принимать на основе пробы с элементами 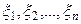. Предположим, что возможные решения могут быть 
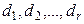. Решение принимается на основе исследования пробы 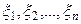, т.е. дается объяснение -мерной решающей функции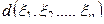 
, возможными значениями которой являются возможные решения .
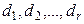Пусть обозначаются суммарные расходы через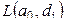 
, если предположить, что значением параметра 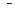является 
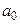и в результате исследования пробы 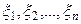принято решение 
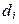. Зная функци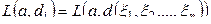и 
и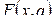 
(функция распределения), математическое ожидание расходов станет исчислимым при условии 
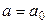. Пусть такое математическое ожидание обозначается через
.
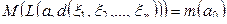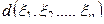Количество элементов пробы и решающую функцию следует выбирать таким образом, чтобы значение 
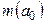было по возможности мало при любом значении 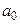, или иными словами, ищутся такое значение и такая функция 
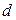, для которых значение 
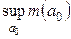является минимальным.
Такой вывод делается на основе рассуждений, проводимых по теории игр. Представим себе, что статистик и «природа» играют; в этой игре природа имеет право выбирать значение параметра 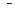, а правом статистика является выбирать решающую функцию. Иначе говоря, стратегиями природы являются возможные значения параметра 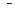, а стратегиями статистика – возможные решения. (Такая игра обычно не является конечной). По рассуждениям, проводимым в соответствии с теорией игр, очевидно, что самая хорошая стратегия статистика будет такая, что он случайно выбирает решение из возможных решений с некоторым распределением вероятностей.
Другой результат будет получен, если параметр 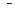рассматривается как случайная переменная. Тогда ситуация рассматривается таким образом, что значение 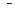является числом, зависящим от различных случайных факторов в некотором объеме товара, доставляемого в разных случаях. Предположим, что известна функция распределения 
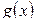случайной переменной 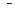, тогда величина 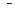также представляет собой случайную переменную. В таком случае статистический метод целесообразно выбирать таким образом, чтобы значение математического ожидания 
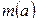было минимальным.
Дата: 2019-03-05, просмотров: 404.
