Средней и дисперсии
11.1. Равноотстоящие варианты
Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае удобно находить выборочную среднюю и дисперсию методом произведений по формулам
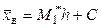 ,
, 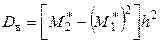 ,
,
где 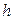 - шаг (разность между двумя соседними вариантами);
- шаг (разность между двумя соседними вариантами); 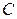 - ложный нуль (варианта, которая расположена примерно в середине вариационного ряда);
- ложный нуль (варианта, которая расположена примерно в середине вариационного ряда); 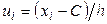 - условная варианта;
- условная варианта; 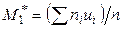 - условный момент первого порядка;
- условный момент первого порядка; 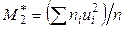 - условный момент второго порядка.
- условный момент второго порядка.
Пример 11.1. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема 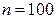 :
:
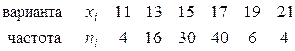 .
.
Решение. Составим расчетную табл. 11.1; для этого:
1) запишем варианты в первый столбец;
2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;
3) в качестве ложного нуля 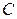 выберем варианту (17), которая имеет наибольшую частоту (в качестве
выберем варианту (17), которая имеет наибольшую частоту (в качестве 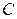 можно взять любую варианту, расположенную примерно в середине столбца); в клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0; над нулем последовательно записываем -1, -2, -3 а под нулем 1, 2;
можно взять любую варианту, расположенную примерно в середине столбца); в клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0; над нулем последовательно записываем -1, -2, -3 а под нулем 1, 2;
4) произведения частот 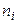 на условные варианты
на условные варианты 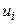 запишем в четвертый столбец; отдельно находим сумму (А1=--74) отрицательных чисел и отдельно сумму (А2=14) положительных чисел; сложив эти числа, их сумму (-60) помещаем в нижнюю клетку четвертого столбца;
запишем в четвертый столбец; отдельно находим сумму (А1=--74) отрицательных чисел и отдельно сумму (А2=14) положительных чисел; сложив эти числа, их сумму (-60) помещаем в нижнюю клетку четвертого столбца;
5) произведения частот на квадраты условных вариант, т.е. 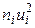 , запишем в пятый столбец (удобнее перемножить числа каждой строки третьего и четвертого столбцов;
, запишем в пятый столбец (удобнее перемножить числа каждой строки третьего и четвертого столбцов; 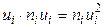 ); сумму чисел столбца (152) помещаем в нижнюю клетку пятого столбца;
); сумму чисел столбца (152) помещаем в нижнюю клетку пятого столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, т.е. 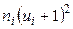 , запишем в шестой контрольный столбец; сумму чисел столбца (132) помещаем в нижнюю клетку шестого столбца.
, запишем в шестой контрольный столбец; сумму чисел столбца (132) помещаем в нижнюю клетку шестого столбца.
В итоге получим расчетную табл. 11.1.
Для контроля вычислений пользуются тождеством
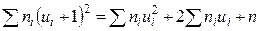 .
.
Контроль:
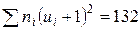 ,
, 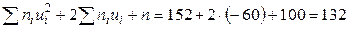 .
.
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков:
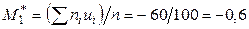 ;
; 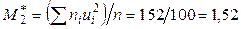 .
.
Найдем шаг (разность между любыми двумя соседними вариантами): 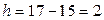 .
.
Вычислим искомые выборочные среднюю и дисперсию, учитывая, что ложный нуль (варианта, которая имеет наибольшую частоту) 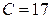 :
:
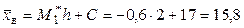 ;
;
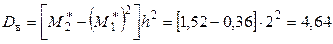 .
.
Таблица 11.1
| 1 | 2 | 3 | 4 | 5 | 6 |
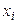
| 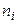
| 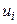
| 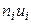
| 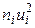
| 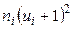
|
| 11 | 4 | -3 | -12 | 36 | 16 |
| 13 | 16 | -2 | -32 | 64 | 16 |
| 15 | 30 | -1 | -30 | 30 | 0 |
| 17 | 40 | 0 | А1=-74 | 40 | |
| 19 | 6 | 1 | 6 | 6 | 24 |
| 21 | 4 | 2 | 8 | 16 | 36 |
| А2=14 | |||||
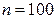
| 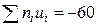
| 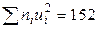
| 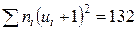
|
11.2. Неравноотстоящие варианты
Если первоначальные варианты не являются равноотстоящими, то интервал, в котором заключены все варианты выборки, делят на несколько равных, длины 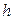 , частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.
, частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.
При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой (особенно при малом числе интервалов), делают поправку Шеппарда, а именно вычитают из вычисленной дисперсии 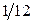 квадрата длины частичного интервала.
квадрата длины частичного интервала.
Таким образом, с учетом поправки Шеппарда дисперсию вычисляют по формуле
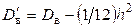 .
.
Пример 11.2. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема 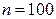 :
:
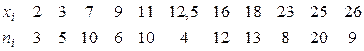 .
.
Решение. Разобьем интервал 2-26 на следующие четыре частичных интервала длины  .приняв середины частичных интервалов в качестве новых вариант
.приняв середины частичных интервалов в качестве новых вариант 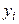 , получим равноотстоящие варианты:
, получим равноотстоящие варианты: 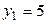 ,
, 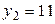 ,
, 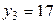 ,
, 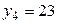 .
.
В качестве частоты 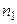 варианты
варианты 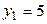 примем сумму частот вариант, попавших в первый интервал:
примем сумму частот вариант, попавших в первый интервал: 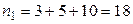 .
.
Вычислим аналогично частоты остальных вариант, получим распределение равноотстоящих вариант:
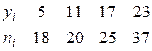
Пользуясь методом произведений, найдем 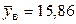 ,
, 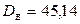 .
.
Принимая во внимание, что число частичных интервалов (4) мало, учтем поправку Шеппарда:
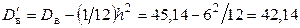 .
.
Дата: 2019-03-05, просмотров: 372.