В случае, когда нет никакой информации о функции распределения некоторой случайной переменной, приходится оценивать полную функцию распределения из элементов пробы.
Пусть 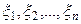 представляет собой пробу из
представляет собой пробу из 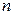 элементов, а упорядоченная проба, полученная из данной пробы, обозначается символом
элементов, а упорядоченная проба, полученная из данной пробы, обозначается символом 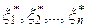 . Функция распределения, основанная на опыте
. Функция распределения, основанная на опыте 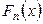 , определяется следующим образом:
, определяется следующим образом:
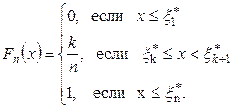 . (3.6)
. (3.6)
Поскольку функция 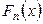 является относительной частотой такого события, при котором результат эксперимента меньше, чем
является относительной частотой такого события, при котором результат эксперимента меньше, чем 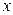 и функция
и функция 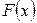 (неизвестная функция распределения) является вероятностью такого же события, то по законам больших чисел функция
(неизвестная функция распределения) является вероятностью такого же события, то по законам больших чисел функция 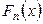 будет близка к функции
будет близка к функции 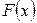 с большой вероятностью при достаточно большом
с большой вероятностью при достаточно большом 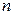 . Это означает, что функцию
. Это означает, что функцию 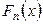 можно считать некоторой оценкой функции
можно считать некоторой оценкой функции 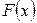 .
.
Гистограмма. Для оценки функции плотности применяется так называемая гистограмма. Гистограмма пробных элементов 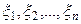 может быть получена следующим образом. Предположим, что все полученные пробные элементы находятся между числами
может быть получена следующим образом. Предположим, что все полученные пробные элементы находятся между числами 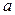 и
и 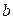 , т.е.
, т.е.
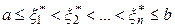 . (3.7)
. (3.7)
Разделим интервал 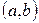 на
на 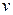 одинаковых частей с точками разделения
одинаковых частей с точками разделения 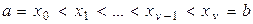 и рассчитаем относительную частоту такого события, при котором некоторый пробный элемент попадает между точками
и рассчитаем относительную частоту такого события, при котором некоторый пробный элемент попадает между точками 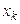 и
и 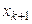 . Если данную относительную частоту изобразить вертикально над интервалом
. Если данную относительную частоту изобразить вертикально над интервалом 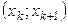 , то получится гистограмма. Путем соответствующего выбора значения
, то получится гистограмма. Путем соответствующего выбора значения 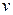 (следует выбирать примерно
(следует выбирать примерно 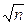 ) может быть достигнуто состояние, при котором гистограмма будет близка к функции плотности с большой вероятностью.
) может быть достигнуто состояние, при котором гистограмма будет близка к функции плотности с большой вероятностью.
Статистическое распределение выборки
Пусть для изучения количественного (дискретного или непрерывного) признака  из генеральной совокупности извлечена выборка
из генеральной совокупности извлечена выборка 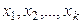 объема
объема 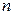 . Наблюдавшиеся значения
. Наблюдавшиеся значения 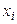 признака
признака  называют вариантами, а последовательность вариантов, записанных в возрастающем порядке, - вариационным рядом.
называют вариантами, а последовательность вариантов, записанных в возрастающем порядке, - вариационным рядом.
Статистическими распределениями выборки называют перечень вариант 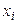 вариационного ряда и соответствующих им частот
вариационного ряда и соответствующих им частот 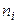 (сумма всех частот равна объему выборки
(сумма всех частот равна объему выборки 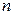 ) или относительных частот
) или относительных частот 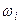 (сумма всех относительных частот равна 1). Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал) [1].
(сумма всех относительных частот равна 1). Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал) [1].
Пример 4.1. Выборка задана в виде распределения частот:
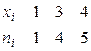 .
.
Найти распределение относительных частот.
Решение. Найдем объем выборки 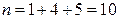 . Найдем относительные частоты:
. Найдем относительные частоты:
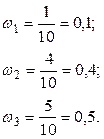
Напишем искомое распределение относительных частот:
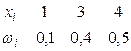 .
.
Контроль: 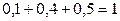 .
.
Дата: 2019-03-05, просмотров: 347.