При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
Виды проявления количественных связей между признаками
функциональная связь
корреляционная связь
Определения функциональной и корреляционной связи
Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
Практическое значение установления корреляционной связи. Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Величина, характеризующая направление и силу связи между признаками. Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
Способы представления корреляционной связи
график (диаграмма рассеяния)
коэффициент корреляции
Направление корреляционной связи
прямая
oбратная
Сила корреляционной связи
сильная: ±0,7 до ±1
средняя: ±0,3 до ±0,699
слабая: 0 до ±0,299
Методы определения коэффициента корреляции и формулы
метод квадратов (метод Пирсона)
ранговый метод (метод Спирмена)
Методические требования к использованию коэффициента корреляции
измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
расчет может производиться с использованием абсолютных или производных величин
для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
число наблюдений не менее 30
Рекомендации по применению метода ранговой корреляции (метод Спирмена)
когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
когда признаки представлены не только количественными, но и атрибутивными значениями
когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
Рекомендации к применению метода квадратов (метод Пирсона)
когда требуется точное установление силы связи между признаками
когда признаки имеют только количественное выражение
Методика и порядок вычисления коэффициента корреляции
1) Метод квадратов
построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно х и у;
определить для каждого вариационного ряда средние значения (М1 и М2);
найти отклонения (dх и dy) каждого числового значения от среднего значения своего вариационного ряда;
полученные отклонения перемножить (dx X dy)
каждое отклонение возвести в квадрат и суммировать по каждому ряду (Σ dx2 и dy2 )
подставить полученные значения в формулу расчета коэффициента корреляции:
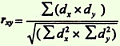
при наличии вычислительной техники расчет производится по формуле:
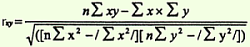
2) Ранговый метод
составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют
величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин
определить разность рангов между х и у (d): d = х — у
возвести полученную разность рангов в квадрат (d2)
получить сумму квадратов разности (Σ d2) и подставить полученные значения в формулу:
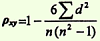
Схема оценки корреляционной связи по коэффициенту корреляции
| Сила связи | Направление связи | |
| прямая (+) | обратная (-) | |
| Сильная | от + 1 до +0,7 | от - 1 до - 0,7 |
| Средняя | от + 0,699 до + 0,3 | от - 0,699 до - 0,3 |
| Слабая | от + 0,299 до 0 | от - 0,299 до 0 |
Вычисление ошибки коэффициента корреляции
ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):
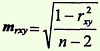
ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):
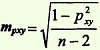
Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов
Способ 1
Достоверность определяется по формуле:
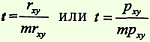
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.
| Задача - эталон |
на применение метода квадратов
Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.
Таблица 1
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) |
| 4 8 11 27 34 37 | 28 56 77 191 241 262 |
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.
Решение.
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) | dх | dу | dх х dу | dx2 | dy2 |
| 4 8 11 27 34 37 | 28 56 77 191 241 262 | -16 -12 -9 +7 +14 +16 | -114 -86 -66 +48 +98 +120 | 1824 1032 594 336 1372 1920 | 256 144 81 49 196 256 | 12996 7396 4356 2304 9604 14400 |
| Мх=Σ х / n | Му=Σ у / n |
| Σ dх x dу=7078 | Σ dх2=982 | Σ dy2=51056 | |
| Мх=120/6=20 | Мy=852/6=142 |
| ||||
Определить средние величины Mx ряду вариант "х" и Му в ряду вариант "у" по формулам:
Мх = Σх/n (графа 1) и
Му = Σу/n (графа 2)
Найти отклонение (dх и dу) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у"
dх = х — Мх (графа 3) и dy = у — Му (графа4).
Найти произведение отклонений dx х dy и суммировать их: Σ dх х dу (графа 5)
Каждое отклонение dx и dу возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ dx2 = 982 (графа 6) и Σ dy2 = 51056 (графа 7).
Определить произведение Σ dx2 х Σ dy2 и из этого произведения извлечь квадратный корень
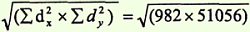
Полученные величины Σ (dx x dy) и √(Σdx2 x Σdy2) подставляем в формулу расчета коэффициента корреляции:
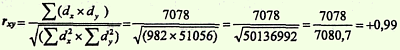
Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mrxy) и критерий t по формулам:
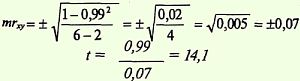
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
2-й способ. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции" (см. приложение 1). При числе степеней свободы (n — 2)=6 - 2=4, наш расчетный коэффициент корреляции rxу = + 0,99 больше табличного (rтабл = + 0,917 при р = 99%).
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: rху = + 0,99, р > 99,9%).
| Задача - эталон |
на применение рангового метода
Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
| Стаж работы в годах | Число травм на 100 работающих |
| до 1 года 1-2 3-4 5-6 7 и более | 24 16 12 12 6 |
Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака "стаж работы в годах" имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод — метод квадратов.
Решение. Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.
Таблица 2
| Стаж работы в годах | Число травм | Порядковые номера (ранги) | Разность рангов | Квадрат разности рангов | |
| X | Y | d(х-у) | d2 | ||
| До 1 года | 24 | 1 | 5 | -4 | 16 |
| 1-2 | 16 | 2 | 4 | -2 | 4 |
| 3-4 | 12 | 3 | 2,5 | +0,5 | 0,25 |
| 5-6 | 12 | 4 | 2,5 | +1,5 | 2,25 |
| 7 и более | 6 | 5 | 1 | +4 | 16 |
|
| Σ d2 = 38,5 | ||||
Каждый из рядов парных признаков обозначить через "х" и через "у" (графы 1—2).
Величину каждого из признаков заменить ранговым (порядковым) номером. Порядок раздачи рангов в ряду "x" следующий: минимальному значению признака (стаж до 1 года) присвоен порядковый номер "1", последующим вариантам этого же ряда признака соответственно в порядке увеличения 2-й, 3-й, 4-й и 5-й порядковые номера — ранги (см. графу 3).
Аналогичный порядок соблюдается при раздаче рангов второму признаку "у" (графа 4).
В тех случаях, когда встречаются несколько одинаковых по величине вариант (например, в задаче-эталоне это 12 и 12 травм на 100 работающих при стаже 3—4 года и 5—6 лет, порядковый номер обозначить средним числом из суммы их порядковых номеров. Эти данные о числе травм (12 травм) при ранжировании должны занимать 2 и 3 места, таким образом среднее число из них равно (2 + 3)/2 = 2,5.
Таким образом, числу травм "12" и "12" (признаку) следует раздать ранговые номера одинаковые — "2,5" (графа 4).
Определить разность рангов d = (х — у) — (графа 5)
Разность рангов возвести в квадрат (d2) и получить сумму квадратов разности рангов Σ d2 (графа 6).
Произвести расчет коэффициента ранговой корреляции по формуле:
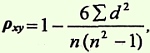
где n — число сопоставляемых пар вариант в ряду "x" и в ряду "у"
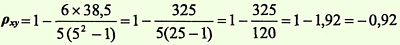
Определить достоверность коэффициента ранговой корреляции.
1-й способ. Определить ошибку (mрху) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:
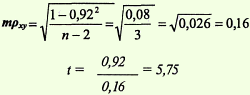
Полученный критерий t = 5,75 соответствует вероятности безошибочного прогноза (р) больше 95 %:
рху = - 0,92; mрху = ± 0,16; t = 5,75; р > 95%
2-й способ. По таблице "Стандартных коэффициентов корреляции": при числе степеней свободы (n - 2) = 5 - 2 = 3 наш расчетный коэффициент корреляции рху = - 0,92 больше табличного 0,878 и меньше 0,933, что соответствует вероятности безошибочного прогноза больше 95% и меньше 98%. Это позволяет считать полученный коэффициент ранговой корреляции достоверным.
Вывод. С вероятностью безошибочного прогноза (р) больше 95% установлено, что чем больше стаж работы, тем меньше частота травм (связь обратная, сильная, достоверная корреляционная: рху = - 0,92, p > 95%.
| Приложение 1. |
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
| Число степеней свободы — 2 | Уровень вероятности р (%) | ||
| 95% | 98% | 99% | |
| 1 | 0,997 | 0,999 | 0,999 |
| 2 | 0,950 | 0,980 | 0,990 |
| 3 | 0,878 | 0,934 | 0,959 |
| 4 | 0,811 | 0,882 | 0,917 |
| 5 | 0,754 | 0,833 | 0,874 |
| 6 | 0,707 | 0,789 | 0,834 |
| 7 | 0,666 | 0,750 | 0,798 |
| 8 | 0,632 | 0,716 | 0,765 |
| 9 | 0,602 | 0,885 | 0,735 |
| 10 | 0,576 | 0,858 | 0,708 |
| 11 | 0,553 | 0,634 | 0,684 |
| 12 | 0,532 | 0,612 | 0,661 |
| 13 | 0,514 | 0,592 | 0,641 |
| 14 | 0,497 | 0,574 | 0,623 |
| 15 | 0,482 | 0,558 | 0,606 |
| 16 | 0,468 | 0,542 | 0,590 |
| 17 | 0,456 | 0,528 | 0,575 |
| 18 | 0,444 | 0,516 | 0,561 |
| 19 | 0,433 | 0,503 | 0,549 |
| 20 | 0,423 | 0,492 | 0,537 |
| 25 | 0,381 | 0,445 | 0,487 |
| 30 | 0,349 | 0,409 | 0,449 |
| Источник |
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., "Гэотар-Медиа", 2007, учебное пособие для вузов
| Литература |
Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина, 2003. — 368 с.
Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.
Основные теоретические положения темы:
При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой-либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
Все явления в природе и в обществе находятся во взаимной связи. Различают две формы проявления количественных связей между признаками: функциональную и корреляционную.
Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-химических процессов.
Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для социально-гигиенических процессов, клинической медицины и биологии.
Практическое значение установления корреляционной связи:
1. Выявление причинно-следственной связи между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.).
2. Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Корреляционный анализ позволяет изучить взаимодействие факторов, измерить “силу” характер и направленность влияния одних факторов на другие.
Величиной, характеризующей направление и силу связи между признаками, является коэффициент корреляции. Корреляционная связь может быть представлена таблицей, графиком (диаграмма рассеяния) или коэффициентом корреляции.
Измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту). Расчет может производиться с использованием как абсолютных, так и производных величин.
Для вычисления коэффициента корреляции используются несгруппированные данные (это требование применяется только при вычислении коэффициента корреляции по методу квадратов). Число наблюдений не менее 30.
Коэффициент корреляции одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ±1.
| Сила связи | Характер связи | |
| Прямая (+) | Обратная (–) | |
| Полная | +1 | –1 |
| Сильная | От +0,9 до +0,7 | От –0,9 до –0,7 |
| Средняя | От +0,6 до +0,3 | От –0,6 до –0,3 |
| Слабая | От +0,2 до 0 | От –0,2 до 0 |
| Связь отсутствует |
По характеру зависимость между факторами может быть линейной, когда при изучении одного фактора другой также пропорционально меняется и криволинейной, когда происходят непропорциональные изменения.
По направленности влияние одного фактора на другой бывает положительным, когда с увеличением одного фактора, другой также увеличивается, и отрицательным, когда при увеличении одного фактора, другой уменьшается.
Метод ранговой корреляции применяется в тех случаях, когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных, когда признаки не только количественные, но и атрибутивные и ряды распределения признаков имеют открытые варианты (например: стаж работы до 1 года).
Оценка достоверности коэффициента корреляции определяется в зависимости от метода вычисления коэффициента корреляции:
Ошибка коэффициента корреляции, вычисленного методов квадратов (Пирсона):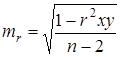 
Ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):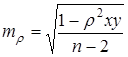 
Критерий достоверности определяется по формуле: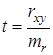 
или 
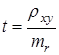, где rxy – коэффициент корреляции, x и y – признаки, между которыми определяется связь, n – число наблюдений.
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n – 2), где n – число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности P ³ 99%.
Контрольные вопросы:
1) Дайте определение функциональной и корреляционной связи.
2) Приведите примеры прямой и обратной корреляционной связи.
3) Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками.
4) В каких случаях применяется ранговый метод вычисления коэффициента корреляции?
5) Каковы основные этапы вычисления коэффициента корреляции ранговым методом?
6) Как определяется достоверность коэффициента корреляции? Укажите способы.
В ходе статистического исследования этих связей необходимо выявить причинно-следственные зависимости между показателями, т.е. насколько изменение одних показателей зависит от изменения других показателей.
Существует две категории зависимостей (функциональная и корреляционная) и две группы признаков (признаки-факторы и результативные признаки). В отличие от функциональной связи, где существует полное соответствие между факторными и результативными признаками, в корреляционной связи отсутствует это полное соответствие.
Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.
Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.
Важнейшей задачей является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи ( уравнения регрессии).
Могут иметь место различные формы связи:
прямолинейная
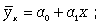(8.1)
криволинейная в виде:
параболы второго порядка (или высших порядков)
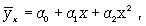(8.2)
гиперболы
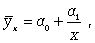(8.3)
показательной функции
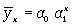(8.4)
и т.д.
Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):
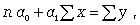
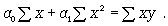(8.5)
Если связь выражена параболой второго порядка (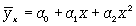 
), то систему нормальных уравнений для отыскания параметров a0 , a1 , a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде
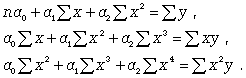(8.6)
Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения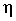 
:
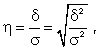(8.7)
где -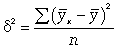 
дисперсия в ряду выравненных значений результативного показателя 
; 
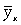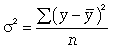- дисперсия в ряду фактических значений у.
Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:
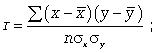(8.8)
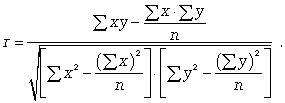
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.
В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.
Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.
Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены 
К. Спирмэном и М. Кендэлом.
Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле
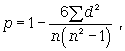(8.9)
где d = Nx - Ny , т.е. разность рангов каждой пары значений х и у; n - число наблюдений.
Ранговый коэффициент корреляции Кендэла (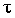 
) можно определить по формуле
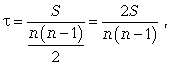(8.10)
где S = P + Q.
К непараметрическим методам исследования можно отнести коэффициент ассоциации Кас и коэффициент контингенции Ккон , которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.
Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:
| Признаки | А (да) | А (нет) | Итого |
| В (да) | a | b | a + b |
| В (нет) | с | d | c + d |
| Итого | a + c | b + d | n |
Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков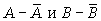 
; n - общая сумма частот.
Коэффициент ассоциации можно расcчитать по формуле
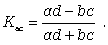(8.11)
Коэффициент контингенции рассчитывается по формуле
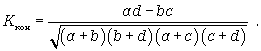(8.12)
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.
Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП ).
Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:
| Признаки | A | B | C | Итого |
| D | m11 | m12 | m13 | ∑m1j |
| E | m21 | m22 | m23 | ∑m2j |
| F | m31 | m32 | m33 | ∑m3j |
| Итого | ∑mj1 | ∑mj2 | ∑mj3 | П |
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.
Коэффициент взаимной сопряженности Пирсона определяется по формуле
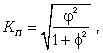(8.13)
где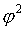 
- показатель средней квадратической сопряженности:
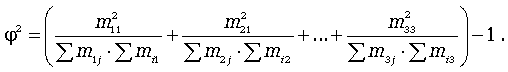
Коэффициент взаимной сопряженности изменяется от 0 до 1.
Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле
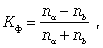(8.14)
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; nb - соответственно количество несовпадений.
Коэффициент Фехнера может изменяться в пределах -1,0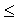 
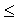Кф +1,0.
Дата: 2019-03-05, просмотров: 320.
