Цель:

1. Ознакомление с параметрическими методами классификации выборки.

2. Изучение оценки параметрических методов результатов статистического исслеования.

Малые выборки. Приведенные выше формулы и построенные на основании их оценочные таблицы применимы только при наличии относительно большого (практически не менее 30) числа наблюдений. При меньшем количестве наблюдений (так называемая малая выб орка), что довольно часто имеет место в клинических и экспериментальных работах, для оценки достоверности результатов прибегают к специальным таблицам. (Напомним, что среднееквадратическ ое отклонение при малых выборках вычисляется по формуле:

).

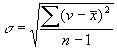Это объясняется тем, что при небольших выборках распределение выборочных средних систематически отклоняется от кривой нормального распределения. Большие отклонения от генеральной средней п ри малых выборках являются более вероятными, чем при больших выборках.

Английский ученый В.Госсет (Стьюдент) исследовал распределение t для малых выборок и установил формулу плотности этого распределения.

Для определения пределов колеблемости полученной по данным малдой выборки средней величины и оценки достоверности различий, сравниваемых средних (относительных величин) используют специальную таблицу критерия t (Стьдента).

В графах 2.3 и 4 таблицы помещены величины доверительного коэффициента (t), показывающие во сколько раз разность сравниваемых величин при данном малом чис ле наблюдений должна превышать свою среднюю ошибку для того, чтобы эта разность могла быть признана достоверной с данным уровнем вероятности, а результаты статистического исследования – достаточно надежными. Числа графы 2-й исчислены для вероятности прав ильного заключения равной 0,95 (95%) и вероятности ошибки – 0,05 (5%), числа графы 3-й – с соответствующими вероятностями 0,99 (99%) и 0,01(1%); числа графы 4-й соответственно – 99,9 и 0,1%. Практически достаточно пользоваться числами графы 3 и даже 2 и только в случае необходимости, особенно большой точности, прибегать к числам графы 4.

Значение коэффициента t (Стьюдента) зависит не только от вероятности (р_t), но и от объема выборки (при n` = n-1). Из таблицы видно, что чем меньше выборка, тем больше значение t.

Обращаться к таблице следует по графе 1, в которой указано число степеней свободы n` = n-1, т.е. числу проведенных наб людений , уменьшенному на единицу. Так, например, если после 8 испытаний действия спинномозговой анестезии на уровень кровяного двления установлено, что средняя величина снижения кровяного давления составляла 5,75 мм при средней ошибке 0,65, то из таблиц ы t видно, что при n` = 8-1 = 7; t =2,36 (графа 2 приложения 11). Это значит, что с вероятностью ошибки не более чем 5% можно утверждать, что размеры снижения кровяного давления при спинномозговой анестезии находятся в пределах 5,75±2,36 х 0,65, т.е. в пределах 5,75±1,53 или 4,22 – 8,26 мм; с вероятностью ошибки не более чем 1% можно утверждать, что ра змеры снижения кровяного давления в результате спинномозговой анестезии составляют 5,75±3,50 х 0,65 (графа 3 приложения 11) или 3.48 – 8,02 мм.

Если оценивается достоверность разности коэффициентов или средних, т.е. 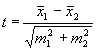, то n₁ + n₂ – 2 .

Среднее падение АД при спинномозговой анестезии 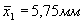, а при эфирном наркозе 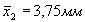; случайна ли разность 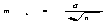или действительно эфирный наркоз вызывает меньшее падение АД, чем спинномозговая анестезия?

Таблица 31. Падение артериального давления в зависимости от вида обезболивания

Вычисления 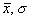и m_x для каждого ряда можно произвести обычным путем, но для упрощения расчетов можно использовать следующую формулу, удобную для применения при малых числах наблюдений :

.

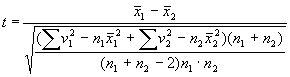Упрощение расчетов при использовании этой формулы достигается тем, что вместо вычисления σ и m ограничиваются определением 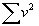для каждого ряда чисел, что значительно облегчает вычислительную работу (v – о тдельные наблюдения, варианты). В данном примере:

Σv₁²= 6²⁺5²+7²+4² +8² +5² =288 , а

Σv²₂ = 2² +3² +4² + 2² +7²+5² 4² +3² =132.

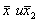как указано было выше, равняются соответственно 5,75 и 3,75; их квадраты .

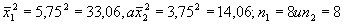Подставив все эти числа в приведенную выше формулу, получим:

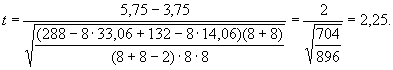
Оценивая t по данным приложения 2, видим, что при n` =8 +8-2=14 в графе 2 этой таблицы стоит величина 2.14. Следовательно, для достоверности утверждения неслучайности различия величин 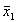и 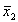, с вероятностью ошибки не более чем 0, 05 (не более чем 5%) достаточно, чтобы t было не менее чем 2.14. В данном примере t =2,25. Значит, действие двух п риведенных видов обезболивания на снидение кровяного давления действительно различно и это различие может считаться статистически доказанным.

Оценка достоверности интенсивных коэффициентов заболеваемости при наличии повторных заболеваний. Формула средней ошибки показателя 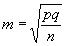пригодна для оценки показателей только в случаях так называемого альтернативного варьирования, т.е. тогда, когда возможны только два исхода (умер или не умер, заболел данной болезнью или не заболел, привить против данного заболевания или не привит и т.п.).

По этой формуле можно исчислять средние ошибки коэффициентов смертности, летальности, а также заболеваемости теми болезнями, которыми, как правило, можно заболеть только один раз (хронические болезни – коронаросклероз, злокачествен ные опухоли, острозаразные заболевания, дающие длительный иммунитет, и т.п.) в течение жизни или хотя бы только один раз за период наблюдения (обычно год).

Определить среднюю ошибку по указанной выше формуле для коэффциентов общей заболеваемости (т.е. заболеваемости всеми болезнями, вместе взятыми) или заболеваемости с временной утратой трудоспособности неправильно.

Практически в течение года человек может болеть несколько раз различными болезнями или даже одной и той же болезнью, длящейся относительно недолго и не дающей стойкого иммунитета (например, грипп, острый катар верхних дыхательных п утей, ангина, пневмония и др.). Случаев временной нетрудоспособности в связи с заболеванием также может быть несколько за год у одного и того же работающего не только в связи с заболеваниями некоторыми острыми болезнями, но и по поводу обострений хрониче ских болезней.

В таких случаях средние ошибки показателей заболеваемости следует рассчитывать по формуле средней ошибки средних величин, т.е.

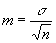, строя вариационные ряды, где вариантами являются числа заболеваний или случаев временной нетрудоспособности в связи с заболеванием в течение года ( 0;1;2;3;4 и т.д.), а частотами – числа болевших данное число раз.

Однако такие расчеты, правильные теоретически, трудно осуществимы на практике, так как требуют кропотливой работы по распределению наблюдаемой группы населения на не болевших ни разу за год, болевших один раз, два раза и т.д.

Трудность этой работы зачастую заставляет вовсе отказываться от расчета средних ошибок коэффициентов заболеваемости, а следовательно, и от статистической оценки достоверности их разности.

В подобной ситуации допустимо приближенное вычисление средней ошибки показателей, предложенное В.А.Мозгляковой. Исходя из предположения, что распределение по числу заболеваний во многих случаях близко к так называемому распределени ю Пуассона, при котором наибольшие частоты соответствуют не средним, а наименьшим вариантам, В.А.Мозглякова предложила в целях упрощения пользоваться расчетом средних квадратических отклонений и средних ошибок уровней заболеваемости по формулам, пригодны м для распределения Пуассона, а именно:

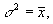а .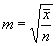

Хорошее соответствие фактического распределения кратности заболеваний теоретическому распределению Пуассона имеет место при числе наблюдений 100-150 и средней величине коэффициента заболев аемости 1,0 на 1 человека. Если коэффициент больше 1.5, то рекомендуемым расчетом не следует пользоваться.

Описанные методы оценки достоверности результатов статистического исследования с помощью критерия t (критерий Стьюдента) в основном пригодны для так называемого нормального распределения, т.е. такого, при котором крайние значения (самые малые и самые большие) вариант встречаются редко, а наиболее часты варианты. Близкие по своей величине к средней арифметической ряда; или для состояния (да-нет, жив-умер и т.п.). Методы оценки достоверности различия параметров таких вариационных рядов называются параметрическими.

Однако характер распределения медико-биологических явлений нередко отличается от нормального. Проводя новые исследования, врач-экспериментатор часто не знает, какому закону варьирования будут следовать результаты, полученные в нескольких опытах, а относительно небольшое число проведенных наблюдений не позволяет ему определить форму распределения. В этих случаях оценку достоверности следует производить с применением так называемых непараметрических критериев.