Это уравнение отражает воздействие на параметры потока формы канала. Для его вывода рассмотрим стационарное течение в канале (G=const). Из уравнения расхода:

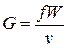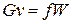, или , (1)

после его дифференцирования имеем:

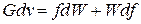. (2)

Разделим выражение (2) на уравнение (1) почленно.

Тогда имеем:

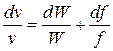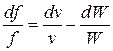, или . (3)

Из уравнения адиабатного процесса

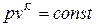, (4)

после дифференцирования получим:

,

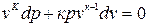или 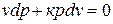. (5)

Разделим выражение (5) на 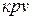. Тогда:

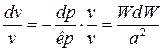. (6)

где 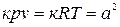; а – скорость звука, м/с; - vdp=WdW – уравнение Бернулли. После подстановки выражения (6) в уравнение (3) имеем:

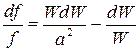, (7)

или

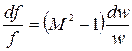, (8)

где 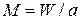- число Маха. Правая часть уравнения обращения воздействий для адиабатного изоэнтропийного течения идеального газа (8) содержит основные параметры потока: число Маха и изменение скорости 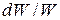, а левая часть – отражает воздействие на течение среды изменения площади поперечного сечения канала df, т.е. формы канала.

Рассмотрим воздействие формы канала df на адиабатное течение в соплах и диффузорах. Сопла – это каналы, в которых происходит расширение газа и увеличение скорости его движения. В диффузорах происходит сжатие газа и уменьшение скорости его движения.

Течение в соплах

Для течения в соплах, где газ расширяется и скорость растет dW>0. При этом знак df будет одинаковым со знаком скобки (М²-1) уравнения (8).

Если на входе в сопло число Маха M<1 и разность (М²-1) – отрицательна, то сопло является суживающимся, т.е. df<0.

Если на входе в сопло число Маха М>1, то разность (М²-1) – положительна и df>0, т.е. сопло – расширяющееся. Увеличение скорости течения при М>1 происходит за счет увеличения площади поперечного сечения канала.

Течение в диффузорах

В диффузорах, где происходит сжатие газа и уменьшение скорости его движения, dW<0 и знак df противоположен знаку выражения (М²-1). При M>1 df<0, т.е. диффузор суживающийся. При M<1 df>0, т.е. диффузор расширяющийся.

Таким образом, один и тот же канал в зависимости от величины скорости газа на входе в канал может работать и как диффузор и как сопло. В суживающемся сопле нельзя достичь скорости газа, большей, чем местная скорость звука. Для получения скорости истечения большей скорости звука должны применяться комбинированные сопла – сопла Лаваля.

15 Сопло́ Лава́ля — газовый канал особого профиля, разгоняющий проходящий по нему газовый поток до сверхзвуковых скоростей. Широко используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.

Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами. Эффективные сопла современных ракетных двигателей профилируются на основании газодинамических расчётов.

Сопло было предложено в 1890 г. шведским изобретателем Густафом де Лавалем для паровых турбин.