Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах. Помимо сугубо практичного применение можно этому закону найти применение и философское ведь что ни говорите, но первый закон термодинамики является выражением одного из самых общих законов природы – закона сохранения энергии. Еще Еклезиаст писал, что ничто ни откуда не появляется и никуда не уходит, все пребывает вечно, постоянно трансформируясь, в этом и кроется вся суть первого закона термодинамики.
7
Второй закон термодинамики, как и первый, является постулатом, обоснованным многовековым опытом человечества. Открытию этого закона способствовало изучение тепловых машин. Французский ученый С. Карно первым показал (1824 г.), что любая тепловая машина должна содержать помимо источника теплоты (нагревателя) и рабочего тела (пар, идеальный газ и др.), совершающего термодинамический цикл, также и холодильник, имеющий температуру обязательно более низкую, чем температура нагревателя.
Коэффициент полезного действия η такой тепловой машины, работающей по обратимому циклу (циклу Карно), не зависит от природы рабочего тела, совершающего этот цикл, а определяется только температурами нагревателя Т1 и холодильника Т2:
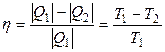 , (3.1)
, (3.1)
где Q1 – количество теплоты, сообщенное рабочему телу при температуре Т1 от нагревателя; Q2 – количество теплоты, отданное рабочим телом при температуре Т2 холодильнику.
Второй закон термодинамики представляет собой обобщение вывода Карно на произвольные термодинамические процессы, протекающие в природе. Известно несколько формулировок этого закона.
Клаузиус (1850 г.) сформулировалвторой закон термодинамики так: невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более горячим.
У. Томсон (Кельвин) (1851 г.) предложил следующую формулировку: невозможно построить периодически действующую машину, вся деятельность которой сводилась бы к совершению механической работы и соответствующему охлаждению резервуара.
Постулат Томсона может быть сформулирован и так: вечный двигатель второго рода невозможен. Вечным двигателем второго рода называют устройство, которое без компенсации полностью превращало бы периодически теплоту какого-либо тела в работу (В.Оствальд). Под компенсациейпонимают изменение состояния рабочего тела или отдачу части теплоты рабочим телом другим телам и изменение термодинамического состояния этих тел при круговом процессе превращения теплоты в работу.
Второй закон термодинамики устанавливает, что без компенсации в круговом процессе ни один джоуль теплоты нельзя превратить в работу.Работа же превращается в теплоту полностью без всякой компенсации. Последнее связано, как отмечалось ранее, с самопроизвольностью процесса рассеивания (обесценивания) энергии.
Второй закон термодинамики вводит функцию состояния системы, которая количественно характеризует процесс рассеивания энергии. В этом смысле приведенные формулировки второго закона термодинамики равноценны, ибо из них следует существование функции состояния системы – энтропии.
В настоящее время второй закон термодинамикиформулируется следующим образом: существует аддитивная функция состояния системы S – энтропия, которая следующим образом связана с теплотой, поступающей в систему, и температурой системы:
Скрыть объявление
 для обратимых процессов; (3.2)
для обратимых процессов; (3.2)
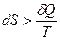 для необратимых процессов. (3.3)
для необратимых процессов. (3.3)
Таким образом, при обратимых процессах в адиабатически изолированной системе ее энтропия не изменяется (dS = 0), а при необратимых процессах увеличивается (dS > 0).
В отличие от внутренней энергии значение энтропии изолированной системы зависит от характера происходящих в ней процессов: в ходе релаксации энтропия изолированной системы должна возрастать, достигая максимального значения при равновесии.
В общем виде второй закон термодинамики для изолированной системы записывается так:
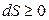 . (3.4)
. (3.4)
Энтропия изолированной системы или увеличивается, если в ней протекают самопроизвольные необратимые процессы, или остается постоянной. Поэтому второй закон термодинамики определяют также как закон о неубывании энтропии в изолированных системах.
Таким образом, второй закон термодинамики дает критерий самопроизвольности процессов в изолированной системе. Спонтанно в такой системе могут протекать только процессы, сопровождающиеся увеличением энтропии. Самопроизвольные процессы заканчиваются с установлением равновесия в системе. Значит, в состоянии равновесия энтропия изолированной системы максимальна. В соответствии с этим критерием равновесия в изолированной системе будет
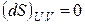 ,
, 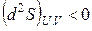 . (3.5)
. (3.5)
Если в процессе принимает участие неизолированная система, то для оценки необратимости (самопроизвольности) процесса необходимо знать изменение энтропии системы dS1 и изменение энтропии окружающей среды dS2. Если принять, что система и окружающая среда (их часто называют «вселенной») образуют изолированную систему, то условием необратимости процесса будет
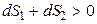 ,
,
то есть процесс будет необратим, если общее изменение энтропии системы и окружающей среды будет больше нуля.
Окружающая среда – огромный резервуар; eе объем и температура не изменяются при теплообмене с системой. Поэтому можно для окружающей среды приравнять δQ = dU и не важно, обратимо или необратимо происходит переход теплоты, так как и δQобр, и δQнеобр точно равны dU окружающей среды. Таким образом, изменение энтропии окружающей среды всегда равно:
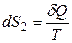 .
.
8.
Рассмотрим произвольный термодинамический процесс расширения газа 1–2–3 в системе координат Pv (рис. 13).
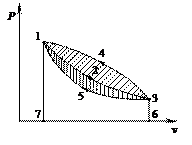
|
| Рис. 13. Прямой и обратный термодинамические циклы. |
В точке 3 в результате расширения газа его давление и температура стали равны давлению и температуре окружающей среды. Площадь под кривой процесса 12367 равна работе расширения. Для возобновления работы данного рабочего тела необходимо возвратить его в первоначальное состояние из точки 3 в точку 1. Это можно осуществить тремя различными путями:
1) по пути 3–2–1, при этом работа расширения будет равна работе сжатия, а суммарная работа цикла равна нулю;
2) по пути 3–4–1, при этом работа сжатия будет больше работы расширения на пл. 12341, а работа цикла будет отрицательной;
3) по пути 3–5–1, при этом работа расширения будет больше работы сжатия на пл. 12351, а суммарная работа цикла будет положительной.
Совокупность последовательно происходящих термодинамических процессов, в результате которых рабочее тело возвращается в первоначальное состояние, называется круговым процессом, или циклом.
Циклы бывают прямые и обратные. Цикл, в результате которого получается положительная работа, называется прямым циклом. По прямым циклам работают все тепловые двигатели. Цикл, для осуществления которого необходимо затрачивать работу, называется обратным циклом. По обратным циклам работают холодильные машины.
В диаграммах Pv и Ts прямые циклы осуществляются по часовой стрелке, обратные – против часовой стрелки.
Рассмотрим произвольный прямой термодинамический цикл 1 кг идеального газа (рис. 14).
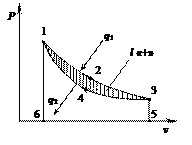
|
| Рис. 14. Прямой термодинамический цикл. |
Цикл 12341 осуществляется по часовой стрелке, следовательно он является прямым. В процессе расширения 1–2–3 за счет подводимой теплоты q1 и снижения внутренней энергии рабочее тело совершает работу расширения, численно равную площади под линией процесса 12356. В процессе сжатия 3–4–1 отводится теплота q2 и повышается внутренняя энергия рабочего тела за счет затраченной работы сжатия, численно равной площади 14356. В результате осуществления прямого цикла получается положительная работа, равная разности между работой расширения и сжатия, и графически изображаемая площадью 12341. Полезно используемое количество теплоты q может быть найдено как разность между подведенной и отведенной теплотой:
 . (4.18)
. (4.18)
Изменение внутренней энергии в цикле Δu = 0, так как рабочее тело возвращается в первоначальное состояние. В соответствии с первым законом термодинамики, подставив Δu в выражение (4.1), получим
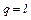 , (4.19)
, (4.19)
т.е. вся полезно используемая в цикле теплота преобразуется в работу.
Эффективность прямого термодинамического цикла (цикла ДВС) оценивается термическим к.п.д. – ηt, определяемым из выражения
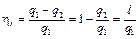 ,
,  . (4.20)
. (4.20)
Рассмотрим произвольный обратный термодинамический цикл 1 кг идеального газа (рис. 15).

|
| Рис. 15. Обратный термодинамический цикл. |
Цикл 12341 осуществляется против часовой стрелки, следовательно, он является обратным. Направление теплоты q1 и q2 в обратном цикле по сравнению с прямым изменяется на противоположное. В процессе расширения 1–2–3 подводится теплота q2 низкого потенциала и снижается внутренняя энергия, рабочее тело совершает работу расширения, численно равную площади под линией процесса 12356. В процессе сжатия 3–4–1 отводится теплота q1 высокого потенциала и повышается внутренняя энергия рабочего тела за счет затраченной работы сжатия, численно равной площади 14356. В обратном цикле работа цикла отрицательная, равна разности между работой расширения и сжатия, и графически изображается площадью 12341, т.е. обратный цикл может осуществляться только при затрате работы от внешнего источника.
Прямой и обратный циклы Карно и их свойства
Цикл Карно - обратимый круговой процесс, в котором совершается наиболее полное превращение теплоты в работу (или работы в теплоту). Термический КПД и холодильный коэффициент цикла Карно не зависят от физических свойств рабочего тела. Прямой (обратный) цикл Карно имеет максимально возможный термический КПД (холодильный коэффициент) в заданном интервале температур.
Т.к. ht цикла Карно всегда больше 1, не зависит от рода рабочего тела и имеет наибольшее значение по сравнению с ht любых других циклов, ограниченных тем же интервалом температур, то:
а) никакими новыми конструкциями тепловых двигателей или применением новых рабочих тел нельзя всю подведенную в цикле теплоту превратить в полезную работу;
б) для увеличения ht нужно стремиться к таким процессам, образующим цикл, в которых средняя температура подвода теплоты была бы как можно больше, а средняя температура отвода теплоты - как можно меньше.
1. Прямой цикл Карно
 а
а
|  б
б
|
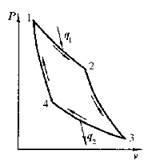
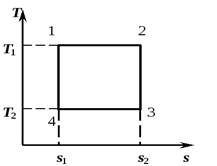
Рис. 6.2. Прямой цикл Карно: а- в vP-диаграмме; б- в sT-диаграмме
Два процесса 1-2 и 3-4 (рис. 6.2) протекают при постоянных температурах, причем Т1- температура горячего источника (нагревателя), Т2 – температура холодного источника (холодильника, т.е. Т1>Т2. Процессы 2-3 и 4-1 - адиабатные. В соответствии с первым законом термодинамики

Внутренняя энергия при Т = const не меняется, а изменение внутренней энергии в адиабатных процессах, протекающих в одном и том же интервале температур, одно и то же, поэтому работа цикла:
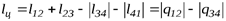
и термический КПД
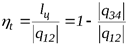
Согласно sT-диаграмме:
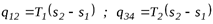 , тогда
, тогда
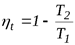 . (6.4)
. (6.4)
Таким образом, КПД цикла Карно определяется обращением температур горячего и холодного источников теплоты. Его значение возрастает при увеличении Т1 или уменьшении Т2. В случае отсутствия перепада температур h t = 0. Цикл Карно состоит из обратимых процессов и поэтому является обратимым.
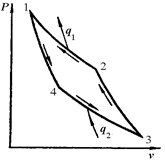
2. Обратный цикл Карно
 а
а
|  б
б
|
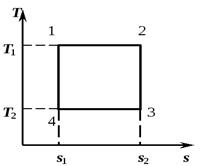
Рис. 6.2. Обратный Карно: а- в vP-диаграмме; б- в sT-диаграмме
Обратный цикл Карно характеризуется затрачиваемой извне работой 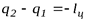 . При этом теплота от холодного источника передается горячему. Это цикл холодильной машины. Ее холодильный коэффициент всегда больше 1:
. При этом теплота от холодного источника передается горячему. Это цикл холодильной машины. Ее холодильный коэффициент всегда больше 1:
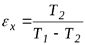 (6.5)
(6.5)
Аналитическое выражение iIзакона термодинамики.
Для обратимого цикла Карно имеем:
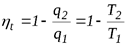 ,
,
тогда 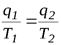 или
или 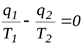 .
.
Если учесть в этом соотношении, что q1 >0 (теплота подводится к рабочему телу) и q2<0 (теплота отводится от рабочего тела), то
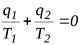 или
или  (6.6)
(6.6)
Отношение подводимой или отводимой теплоты к соответствующей абсолютной температуре называется приведенной теплотой. Выражение (6.6) показывает, что алгебраическая сумма приведенных теплот для обратимого цикла Карно равна нулю, т.е.
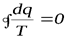 . (6.7)
. (6.7)
Отношение 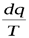 считаютполным дифференциалом функции состояния
считаютполным дифференциалом функции состояния 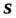 , называемой энтропией. Т.к.dq = Tds, то
, называемой энтропией. Т.к.dq = Tds, то
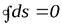 (6.8)
(6.8)
Таким образом, алгебраическая сумма приведенных теплот для любого обратимого цикла равна нулю. Энтропия рабочего тела в результате совершения произвольного обратимого цикла не изменяется.
Уравнение (6.8), выведенное Клаузиусом в 1854 году, представляет собой аналитическое выражение II закона термодинамики для произвольного обратимого цикла и называется первым интегралом Клаузиуса.
В цикле с необратимыми процессами при прочих равных условиях работа, совершаемая рабочим телом меньше, чем в цикле с обратимым процессом, и при одинаковх температурах источника теплоты и холодильника
h tнеобр < h t
Поэтому при наличии в цикле необратимых процессов:
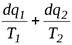 <0 (6.9)
<0 (6.9)
или после интегрирования по контуру
 <0 (6.10)
<0 (6.10)
Это неравенство представляет собой аналитическое выражение II закона термодинамики для произвольного необратимого цикла и называется вторым интегралом Клаузиуса.
Объединяя (6.7) и (6.10), можно записать одно уравнение II закона термодинамики для обратимых (=) и необратимых (<) циклов:
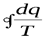 £0 (6.11)
£0 (6.11)
Энтропия есть функция состояния рабочего тела, поэтому изменение энтропии как для обратимого, так и необратимого процессов будет одним и тем же.
Для элементарного необратимого процесса
 >
> 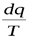 (6.12)
(6.12)
9
Термодинамическим процессом называется последовательное и взаимосвязанное изменение состояния термодинамической системы в результате её взаимодействия с окружающей средой. Исследование термодинамических процессов идеальных газов Идеальный газ в действительности не существует - это модель газа. Использование в термодинамике понятия идеального газа, с одной стороны, упрощает изучение процессов, а с другой стороны, даёт результаты близкие реальному газу, взятому при малых давлениях. ставит своей целью разработать методы расчёта параметров состояния системы в процессе, а также теплоты и работы процесса.
Изучение работы тепловых машин показывает, что наибольший интерес для практики представляют некоторые частные случаи, когда значение одного из параметров остаётся постоянным. Такие процессы называются изопроцессами. К ним относятся изохорный (х=const), изобарный (p=const), изотермный (T=const) и изоэнтропный (s=const). Наряду с изопроцессами рассматриваются политропные процессы, которые являются, с одной стороны, обобщением изопроцессов идеальных газов, а с другой стороны, они сами могут рассматриваться как разновидность изопроцессов, так как для них постоянны работоёмкость CW и показатель политропы n.
Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v=соnst. Из уравнения состояния идеального газа (4) следует, что р/Т =R=v=соnst т.е.давление газа прямо пропорционально его абсолютной температуре:
р2/р1=Т2 /Т1 (41)
Работа расширения в этом процессе равна нулю, так как dv =0.
Количество теплоты, подведенной к рабочему телу в процессе 12 при cv=const, определяется из соотношений (26):
q= 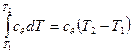 (42)
(42)
При переменной теплоемкости
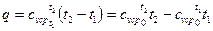 (43)
(43)
где са |  - средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.
- средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.
На рис. 11. представлен график процесса.

Так как t = 0, то в соответствии с первым законом термодинамики ∆u = q и
∆u = сv(Т2 – Т1) при сv = соnst;
∆u = сv |  при сv = vаr (44)
при сv = vаr (44)
Поскольку внутренння энергия идеального газа является функцией только его температуры, то формулы (44) справедливы для любого термодинамического процесса идеального газа.
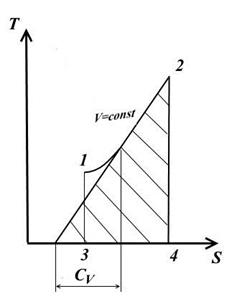
Изменение энтропии визохорном процессе определяется:
s2 – s1 = сv ln (Т2/Т1), (45)
т. е. зависимость энтропии от температуры на изохоре при сv = соnst имеет логарифмический характер (см. рис. 4.1).
Изобарный процесс. Из уравнения состояния идеального газа (4) при р = = соnst находим v/Т= R/р = соnst, или
v2/v1 = Т2/Т1 (46)
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.). На рис. 12 изображен график процесса. Из выражения 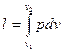 следует, что
следует, что
Скрыть объявление
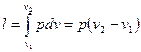 (47)
(47)
Так как pv1 = RT1 и pv2 = RT2, то одновременно
l = R(T2 – T1) (48)
Количество теплоты, сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения (26):
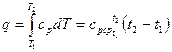 (49)
(49)
где срср - средняя массовая изобарная теплоемкость в интервале температур от t1 до t2 ;при ср = соnst
q = ср(t2 – t1). (50)

|
Рис. 12. Изображение изобарного процесса в р, v- и Т,s – координатах
Измемение энтропии при ср = соnst равно:
s2 – s1 = срln (Т2/Т1) (51)
т. е. температурная зависимость энтропии при изобарном процессе тоже имеет логарифмический характер, но поскольку ср>сv, то изобара в Т, s -диаграмме идет более полого, чем изохора.
Изотермический процесс. При изотермическом процессе температура
постоянна, следовательно, pv=RT=const, или
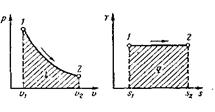
р2/р1 = v1/v2 (52)
т. е. давление и объем обратно пропорциональны друг другу, так что при изо-термическом сжатии давление газа возрастает, а при расширении - падает (закон Бойля — Мариотта, 1662 г.).
|
Графиком изотермического процесса в р,v-координатах, как показывает
уравнение (52), является равнобокая гипербола, для которой координатные оси служат асимптотами (рис.13).
Рис. 13. Изображение изотермического процесса в р, v- и Т, s –координатах
Работа процесса:
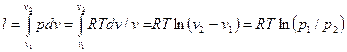 (53)
(53)
Так как температура не меняется, то внутренняя энергия идеального газа в данном процессс остается постоянной (∆u = 0) и вся подводимая к газу теплота полностью превращается в работу расширения:
q=l (54)
При изотермическом сжатии от газа отводится теплота в количестве, равном затраченной иа сжатие работе.
Из соотношений (32) и (52) следует, что изменение энтропии в изотермическом процессе выражается формулой
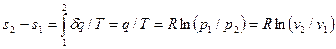 . (55)
. (55)
Адиабатный процесс.Процесс, происходящий без теплообмена с окружающей средой, называется адиабатным, т. е. δq = 0. Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т. е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Как правило, это возможно, ибо теплообмен происходит значителыю медленнее, чсм сжатие или расширение газа.
Уравнения первого закона термодинамики для адиабатного процесса прини-мают вид: срdТ – vdр=0; сv dТ + рdv=0. Поделив первое уравнение на второе, получим
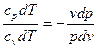 , или
, или 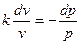
Интегрируя последнее уравнение при условии, что k = ср/сv =соnst, находим
 и
и 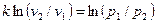 .
.
После потенцирования имеем 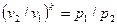 , или
, или
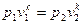 (56)
(56)
Это и есть уравнения адиабаты идеального газа при постоянном отношении теплоемкостей (k = соnst).
Величина
k= ср/сv (57)
называется показателем адиабаты. Подставив ср = сv + R, получим k = 1+Rсv . Согласно классической кинетической теории теплоемкость газов не зависит от температуры,поэтому можно считать, что величина k также не зависит от температуры и определяется числом степеней свободы молекулы. Для одноатомного газа k=1,66, для двухатомного k =1,4, для трех- и многоатомных газов k =1,33.
Поскольку k > 1, то в координатах р, v (рис. 14) линия адиабаты идет круче линии изотермы: при аднабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
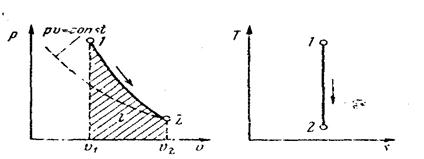
Рис. 14. Изображение адиабатного процесса в р,v- и Т,s- координатах
Определив из уравнения состояния, написанного для состояний 1 и 2, отношение объемов или давлений и подставив их в (56), получим уравнение адиа-батного процесса в форме, выражающей зависимость температуры от обьема или давления:
 ;
;
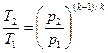 (58)
(58)
Работа расширепия при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по одной из следующих формул:
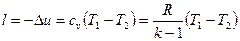 (59)
(59)
Так как при р1v1=RТ1 и р2 v2=RТ2 , то
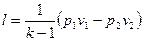 (60)
(60)
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q = 0. Выражение с = δq/dТ показывает, что теплоемкость адиабатного процесса равна нулю.
Поскольку при адиабатном процессе δq = 0, энтропия рабочего тела не изме-няется (ds = 0 и s=соnst). Следовательно, на Т, s- диаграмме адиабатный процесс изображается вертикально.
Политропиый процесс и его обобщающее значение. Любой произвольный процесс можно описать в р, v- координатах (по крайней мере на небольшом участке) уравнением
рvn= соnst , (61)
подбирая соответствующее значение n. Процесс, описываемый уравнением (4.21), называется политропным. Показатель политропы п может принимать любое численное значение в пределах от - ∞ до +∞ , но для данного процесса он является величиной постоянной.
Из уравнения (61) и уравнения Клапейрона нетрудно получить выражения, устанавливающие связь между р, v и Т в любых двух точках на политропе, аналогично тому, как это было сделано для адиабаты:
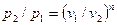 ;
; 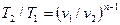 ;
; 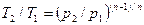 (62)
(62)
Работа расширения газа в политропном процессе имсст вид 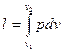 .
.
Так как для политропы в соответствии с (62)
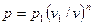 ,
,
то
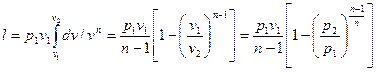 (63)
(63)
Уравнение (63) можно преобразовать к виду:
 ;
;
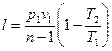 ; (64)
; (64)

Количество подведенной (или отведенной) в процессе теплоты можно определить с помощью уравнения первого закона термодинамики: q=(u2 – u1) + l.
Поскольку u2 – u1 =сv (Т2 — Т1);  , то
, то
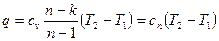 , (65)
, (65)
где
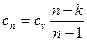 (66)
(66)
представляет собой теплоемкость идеального газа в политропном процессе. При постоянных сv, k и n теплоемкость сn = const, поэтому политропный процесс иногда определяют как процесс с постоянной теплоемкостью. Изменение энтропии
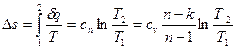 (67)
(67)
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов. Ниже приведены характеристики термодинамических процессов.
Процесс п сn
Изохорный +∞ сv
Изобарный 0 ср
Изотермический 1 ∞
Адиабатный k 0
На рис. 15 показано взаимное расположение на р, v- и Т,s- диаграммах поли-тропных процессов с разными значениями показателя политропы. Все процессы начинаются в одной точке («в центре»).
Изохора (п= ± ∞) делит поле диаграммы на две области: процессы, нахо-дящиеся правее изохоры, характеризуются положительнй работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных правее изохоры, характерна отрицательная работа.
Процессы, расположенные правее и выше адиабаты, идут с подводом теп-лоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты.
Для процессов, расположенных над изотермой (n = 1), характерно увеличе-ние внуиренней энергии газа; процессы, расположенные под изотермой, сопро-вождаются уменьшением внутренней энергии.
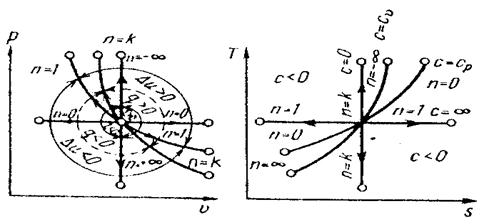
Рис. 15. Изображение основных термодинамических процессов идеального газа в р, v- и Т, s-координатах
Ts-диаграмме
Каждое из этих уравнений содержит два множителя. Один характеризует качество или напряженность энергии (ω2− квадрат скорости, H – высота подъема груза, T – температура, p−давление), а второй – выражает количество или ёмкость тела по отношению к данной энергии (m – масса тела, V− удельный объем, S – энтропия). Первый множитель является интенсивным фактором, а второй – экстенсивным. То есть энтропия представляет собой емкость термодинамической системы по отношению к тепловой напряженности 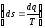 .
.
Клаузиус дал формулировки первого и второго законов термодинамики.
1. Энергия Вселенной постоянна.
2. Энтропия Вселенной стремится к максимуму.
Таким образом, это должно привести к тепловой смерти Вселенной, когда температура выровняется. Но это противоречит, тому, что закон возрастания энтропии получен для изолированной системы.
TS – диаграмма.
На этой диаграмме по оси ординат откладывается температура, а по оси абсцисс – энтропия.
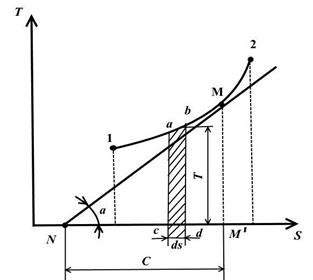
Равновесное состояние в TS− диаграмме изображаются точками с координатами, соответствующими значениям температуры и энтропии.
Обратимый термодинамический процесс изменения состояния рабочего тела от начального состояния 1 до конечного состояния 2 изображается на TS− диаграмме непрерывной кривой, проходящей между этими точками.
Площадь abdc равна TdS=dq, т.е. выражает элементарное количество теплоты, получаемой или отдаваемой системой в обратимом процессе.
Площадь под кривой 1-2 равна
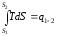 .
.
То есть площадь под кривой в TS− диаграмме, представляет собой теплоту, подведенную к системе или отведенную от нее.
Поэтому TS− диаграмму называют тепловой.
Проведем в произвольной точке M на кривой 1-2 касательную к этой кривой
Величина представляет собой истинную теплоемкость процесса.
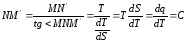
Газовые процессы в TS− диаграмме.
1. Изотермический процесс.
При изотермическом процессе T=const. Поэтому TS− диаграмме он изображается прямой линией, параллельной оси абсцисс.
С учетом того, что dT=0, зависимости изменения энтропии идеального газа в изотермическом процессе примут вид
 (1)
(1)
(уходит слагаемое 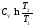 в правой части)
в правой части)
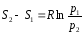 (2)
(2)
Выражение для энтропии идеального газа
 через T,V (1) через T,V (1)
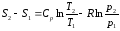 Tp (2) Tp (2)
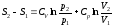 pV (3) pV (3)
|
Процесс 1-2 – это процесс, в котором энтропия увеличивается, а следовательно, к газу подводится теплота и газ совершает работу расширения, эквивалентную этой теплоте.
Процесс2-1− это процесс сжатия, в котором теплота, эквивалентная работе сжатия, отводится от газа и энтропия уменьшается
Площадь фигуры S112 S2 соответствует количеству теплоты q, сообщаемому газу, и одновременно работе l (изотермический процесс)
2. Адиабатный процесс
В адиабатном процессе q=0 и dq=0, а следовательно dS=0.
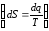
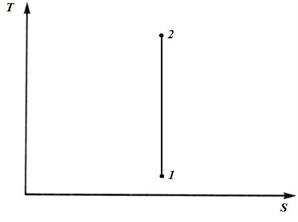
Следовательно, в адиабатном процессе S=const и в TS − диаграмме адиабатный процесс изображается прямой линией, параллельной оси T.
Поскольку в адиабатном процессе S=const,то адиабатные обратимые процессы называют также изоэнтропными.
При адиабатном сжатии температура рабочего тела повышается, а при расширении понижается. Поэтому процесс1-2 – это процесс сжатия, а процесс 2-1 – это расширение.
Из уравнения
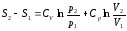 (3)
(3)
При k=const получим 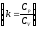

или
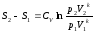 (*)
(*)
Для обратимого адиабатного процесса S1=S2=const, тогда из (*)
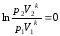
Откуда,
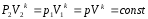
− уравнение адиабаты в координатах p и V.
3. Изохорный процесс
Для изохорного процесса V=const, dV=0.
При постоянной теплоемкости (из ур. (1))
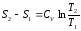 −вид на TS – диаграмме
−вид на TS – диаграмме
Подкасательная к кривой процесса в любой её точке определяет значение истинной теплоёмкости CV.
Подкасательная будет положительной только в том случае, если кривая будет обращена выпуклостью вниз.
Площадь под кривой процесса 1-2 на TS – диаграмме дает в масштабе количество подведенной (или отведенной в процессе 2-1) теплоты q, равное изменению внутренней энергии U2-U1.
4. Изобарный процесс
В изобарном процессе давление постоянное p=const
В этом случае
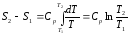 из (2)
из (2)
Следовательно, при p=const как и при V=const изобара является логарифмической кривой, поднимается следа направо и обращена выпуклостью вниз.
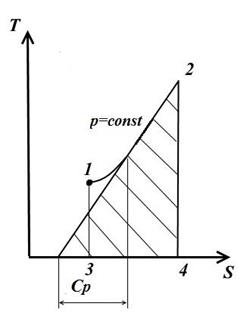
Подкасательная к кривой 1-2 в любой её точке дает значения истинной теплоёмкости Cp.
Площадь под кривой дает кол-во теплоты q, которая сообщается газу при p=const, равное изменению энтальпии i2-i1.
5. Политропный процесс
В политропном процессе 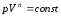 .Теплоёмкость в этом процессе
.Теплоёмкость в этом процессе
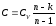
Тогда,
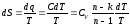
Отсюда, для конечного изменения состояния газа
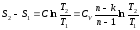
Политропный процесс на TS – диаграмме изображается кривой, расположение которой зависит от показателя n.
6. Круговой процесс. Цикл Карно.
Изобразим в TS – диаграмме произвольный обратимый цикл 1a2b1.
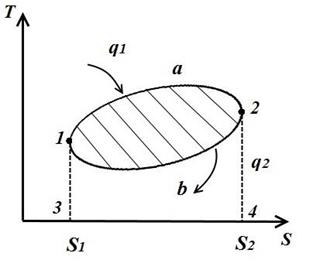
В процессе 1a2 рабочее тело получает кол-во теплоты q1, численно равное площади под кривой 1a2, а в процессе 2-b-1 отдает кол-во теплоты q2, численно равное площади под кривой 2-b-1.
Часть теплоты
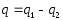
переходит в работу цикла l (∆u=0 в цикле).
Работа цикла положительна, если цикл проходит по часовой стрелке и отрицательна, если против часовой стрелки (направление цикла в pV и TS − диаграммах одинакова).
Термический к.п.д. кругового процесса
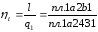
Изменение энтропии в любом цикле равно нулю.
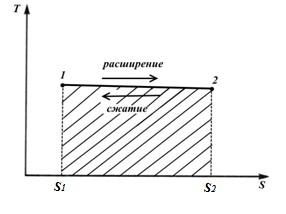
Цикл Карно состоит из двух изотерм и двух адиабат. В TS – диаграмме он будет изображаться в виде прямоугольника (горизонтальные линии – изотермы, вертикальные – адиабаты)
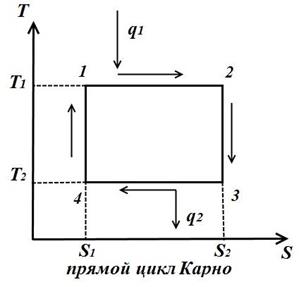
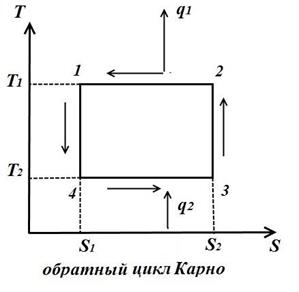
Количество теплоты, подведенное к рабочему телу, числено равно площади прямоугольника 12S2S1:
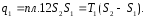
Количество теплоты, отведенное к холодильнику, соответствует площади прямоугольника 34S1S2:
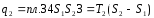
Теплота, эквивалентная работе цикла, равная площади цикла

Термический к.п.д. цикла
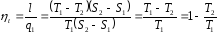
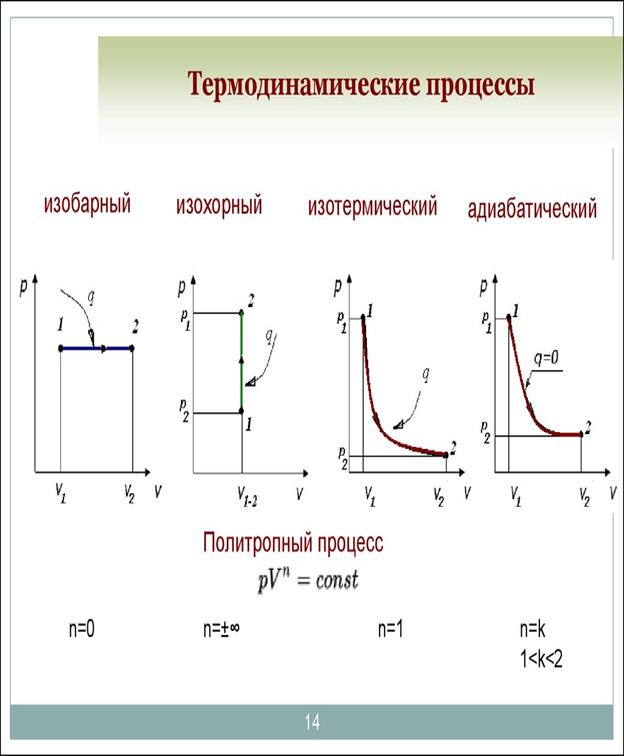
Для обратного цикла (рис. справа)
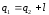
Холодильный коэффициент обратного цикла
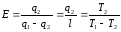
Дата: 2019-03-05, просмотров: 369.