Термодинамическая система, обменивающаяся с окружающей средой веществом, называется открытой. Такие системы широко встречаются в технических устройствах. Примером может служить движение газов и паров в элементах паровых и газовых турбин, магистральных газопроводах, воздуховодах, нагревателях, струйных аппаратах и т. д. При анализе термодинамики потока принимают следующие допущения: поток одномерный; термодинамические параметры и скорость постоянны по всему сечению потока (т. е. рассматриваются их усредненные значения по сечению); поток стационарный, т. е. в любом сечении все величины, характеризующие течение, остаются постоянными во времени, поток является сплошным. Последнее предположение означает, что через любое сечение канала А в единицу времени проходит одно и тоже массовое количество вещества m, кг / с:
m = A·w·ρ = A· w/v = const, (8.1)
где А – поперечное сечение канала, по которому движется поток, м2; w – скорость потока, м/с; ρ – плотность вещества, кг/м3; v – удельный объем вещества, м3/кг.
Это уравнение называется уравнением сплошности или уравнением неразрывности.
В задачу термодинамического анализа процессов, происходящих в потоке, входит выявление зависимостей между различными механическими и термодинамическими величинами, в частности, взаимосвязи между изменением параметров потока р, v, T и скоростью движения рабочего тела как целого w.
Вид этой связи будет зависеть от характера внешних воздействий на поток. К внешним воздействиям на поток, которые будут нами рассматриваться, относятся:
а) геометрическое воздействие, при котором течение происходит в канале переменного сечения;
б) тепловое воздействие, при котором течение сопровождается
подводом или отводом теплоты q;
в) механическое воздействие, при котором течение сопровождается отдачей или затратой технической работы lТ.
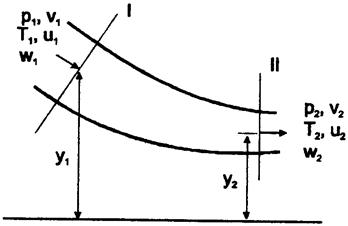
Рассмотрим поток газа через канал произвольной формы (рисунок 8.1), к которому в общем случае подводится теплота q и техническая работа lТ отводится от внешнего объекта или подводится к нему (случай подвижного канала).
Допущения об обратимости процесса течения газов и паров дают возможность применить к потоку через канал основные термодинамические соотношения. Уравнение первого закона термодинамики запишется в этом случае так же, как и для процесса без видимого движения газа:
q = Δu + l,
где l – работа, совершаемая потоком газа или пара (при отсутствии движения газа она целиком состояла из работы, затрачиваемой на преодоление сил внешнего давления).
Рис. 8.1 – Схема потока газа через канал произвольной формы
В случае потока эта работа будет состоять из:
а) работы против сил давления на входе потока в канал и на
выходе из канала lp, которая называется работой проталкивания;
б) работы, затрачиваемой на изменение внешней кинетической
энергии потока lw ;
в) работы, затрачиваемой на изменение внешней потенциальной энергии потока lу;
г) технической работы, которая отбирается от потока (турбинный канал) или подводится к нему (компрессионный канал) lТ.
Таким образом,
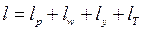 .
.
Результирующая работа газа против внешних сил (работа проталкивания) равна:
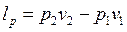 , (8.2)
, (8.2)
где 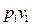 – секундная работа совершенная над газом при входе его в сечение I;
– секундная работа совершенная над газом при входе его в сечение I; 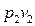 – работа производимая газом при выходе из сечения П.
– работа производимая газом при выходе из сечения П.
Работа, затраченная на изменение внешней кинетической и потенциальной энергии 1 кг потока, соответственно вычисляются так:
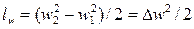 ; (8.3)
; (8.3)
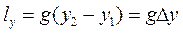 . (8.4)
. (8.4)
Тогда аналитическое выражение первого закона термодинамики для потока примет вид:
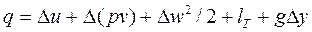 (8.5)
(8.5)
или в дифференциальной форме:
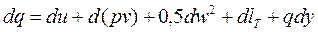 . (8.6)
. (8.6)
Если пренебречь изменением внешней потенциальной энергии и учитывая, что du + d(pv) = dh, имеем:
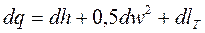 (8.7)
(8.7)
Выражение (8.7) – это первый закон термодинамики для потока. Этот закон утверждает, что теплота, подведенная к потоку рабочего тем от внешнего источника, расходуется на увеличение энтальпии рабочего тела, увеличение кинетической энергии потока и производство технической работы. Если техническая работа отсутствует, то
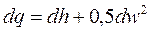 . (8.8)
. (8.8)
При адиабатном процессе уравнение принимает вид:
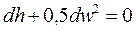 . (8.9)
. (8.9)
После преобразования, уравнение (8.8) примет вид:
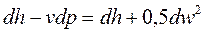 , (8.10)
, (8.10)
откуда
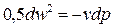 . (8.11)
. (8.11)
Та часть работы расширения, которая превращается в кинетическую энергию и может быть использована в машинах, называется располагаемой работой l0:
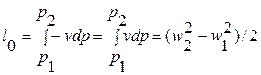 . (8.12)
. (8.12)
Располагаемую работу можно определить по формуле:
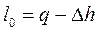 . (8.13)
. (8.13)
Для политропного процесса идеальных газов:
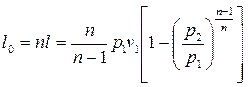 . (8.14)
. (8.14)
Для адиабатного процесса:
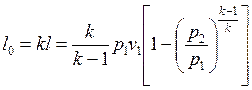 . (
. (
Дата: 2019-03-05, просмотров: 384.