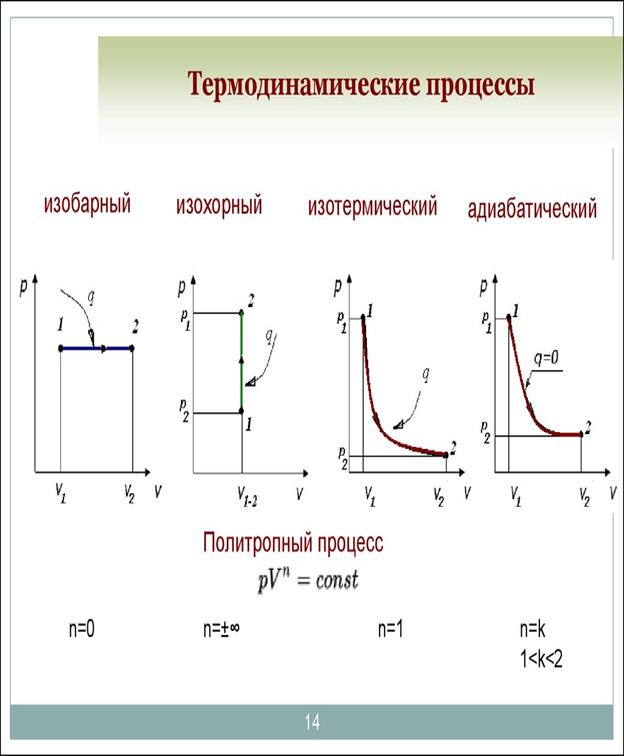
Термодинамика и основы статистики.
Основные понятия.
Моделью материального тела является совокупность атомов и молекул, свойства; законы взаимодействия, движения которых известны. Существует два раздела физики: термодинамика и статическая физика- они изучают закономерности процессов в макротелах, состоящих из атомов и молекул. Они изучают тепловые свойства макротел.
Метод термодинамики -- феноменологический(учитывает превращение энергии без учёта природы исследуемых явлений, связанных с молекулярно-кинетической структурой вещества). Метод статической физики -- исследование системы, состоящей из атомов и молекул путём задания уравнений, описывающих поведение совокупности частиц, и с помощью вероятностного метода определяется поведение макросистемы.
Классическая термодинамика, основоположником которой является Томсон, Клаузиус, изучает равновесные системы и процессы в таких системах.
Неравновесная термодинамика. Она ещё развивается и изучает неравновесные системы.
Основоположниками молекулярно - кинетической теории являются Клаузис, Больцман, Максвелл.
Создателем статической физики является Гиббс. В основе статической физики был положен метод Гиббса для равновесных системы.
Работа расширения
Работа в термодинамике, так же как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.
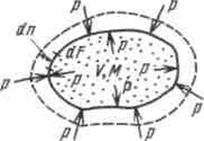
Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.
|
Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ действует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки: 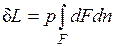 .
.
Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности:  , следовательно
, следовательно
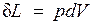 . (3.1)
. (3.1)
При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, равна
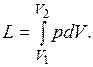
Из (3.1) следует, что 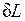 и dV всегда имеют одинаковые знаки:
и dV всегда имеют одинаковые знаки:
если dV>0, то и 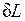 >0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;
>0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;
если же dV<0, то и 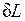 <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ является джоуль (Дж).
<0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ является джоуль (Дж).
Отнеся работу расширения к 1 кг массы рабочего тела, получим
l = L/M; 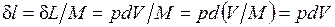 .
.
Величина , представляющая собой удельную работу, совершаемую системой, содержащей 1 кг газа, равна
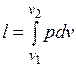 . (3.2)
. (3.2)
Поскольку в общем случае р — величина переменная, то интегрирование возможно лишь тогда, когда известен закон изменения давления р = р(v).
Формулы (3.1) — (3.2) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.
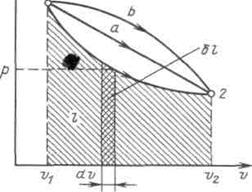
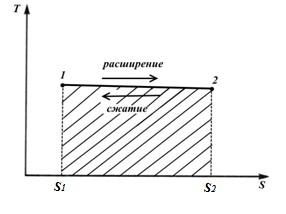
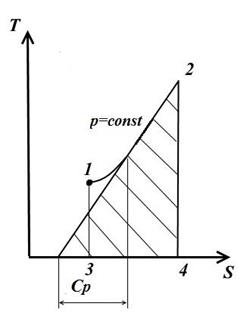
В термодинамике для исследования равновесных процессов широко используют р,v – диаграмму, в которой осью абсцисс служит удельный объем, а осью ординат — давление. Поскольку состояние термодинамической системы определяется двумя параметрами, то на р,v – диаграмме оно изображается точкой. На рисунке точка 1 соответствует начальному состоянию системы, точка 2 — конечному, а линия 12 — процессу расширения рабочего тела от v1 до v2. При бесконечно малом изменении объема площадь заштрихованной вертикальной полоски равна 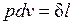 ; следовательно, работа процесса 12 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами.
; следовательно, работа процесса 12 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами.
Таким образом, работа изменения объема эквивалентна площади под кривой процесса в диаграмме р, v (рисунок 3.1).
|
Рисунок 3.1 - Графическое изображение работы в р, v – координатах
Каждому пути перехода системы из состояния / в состояние 2 (например, 12, 1а2 или 1b2) соответствует своя работа расширения.Следовательно, работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояний системы. С другой стороны, 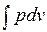 зависит от пути интегрирования и, следовательно, элементарная работа
зависит от пути интегрирования и, следовательно, элементарная работа 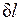 не является полным дифференциалом.
не является полным дифференциалом.
Работа всегда связана с перемещением макроскопических тел в пространстве, например перемещением поршня, деформацией оболочки, поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от одного тела к другому и является мерой переданной энергии. Поскольку величина 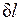 пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные продукты сгорания того или иного топлива.
пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные продукты сгорания того или иного топлива.
Теплота
Помимо макрофизической формы передачи энергии — работы существует также и микрофизическая, т. е. осуществляемая на молекулярном уровне форма обмена энергией между системой и окружающей средой. В этом случае энергия может быть передана системе без совершения работы. Мерой количества энергии, переданной микрофизическим путем, служит теплота.
Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвекцией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности температур между телами.
Как будет показано ниже, элементарное количество теплоты 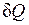 , так же как и L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.
, так же как и L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.
Внутренняя энергия — это свойство самой системы, она характеризует состояние системы. Теплота и работа — это энергетические характеристики процессов механического и теплового взаимодействий системы с окружающей средой. Они характеризуют те количества энергии, которые переданы системе или отданы ею через ее границы в определенном процессе.
Энтальпия
В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:
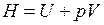 .
.
Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).
Энтальпия обладает свойством аддитивности. Величина
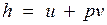 ,
,
называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:
 ;
; 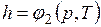 ;
; 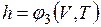 ,
,
а величина dh является полным дифференциалом.
Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.
Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G .
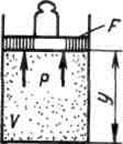
|
Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил: 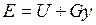 . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа:
. В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: 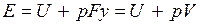 . Получаем, что
. Получаем, что 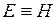 , т.е. энтальпию можно трактовать как энергию расширенной системы.
, т.е. энтальпию можно трактовать как энергию расширенной системы.
Уравнение 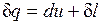 в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения
в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения 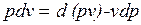 может быть записано в виде
может быть записано в виде 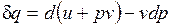 , или
, или
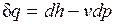 .
.
Из этого соотношения следует, что если давление системы сохраняется неизменным, т. е. осуществляется изобарный процесс (dp=0), то
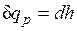 и
и 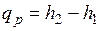 .
.
т. е. теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
Это выражение очень часто используется в расчетах, так как огромное количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбин и реактивных двигателей, теплообменных аппаратах), а также целый ряд процессов химической технологии и многих других осуществляется при постоянном давлении. Кстати, по этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии, а не внутренней энергии.
Для идеального газа с учетом получим
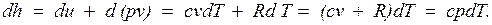
Так как между энтальпией и внутренней энергией существует связь 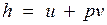 , выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv.
, выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv.
Например, для воды при t=0.01ºC и р =610,8 Па, u = 0, a
h = pv = 0,611 Дж/кг.
При расчетах практический интерес представляет изменение энтальпии в конечном процессе: 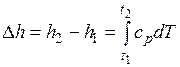 .
.
Энтропия
Как уже указывалось, величина  не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который совершает газ.
не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который совершает газ.
В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты q является абсолютная температура Т.
Покажем это на примере изменения параметров идеального газа в равновесных процессах:
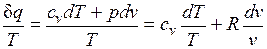 . (3.3)
. (3.3)
Выражение 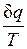 при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К.
при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К.
Таким образом, аналитически энтропия определяется следующим образом:
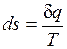 . (3.4)
. (3.4)
Формула (3.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:
 ;
; 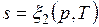 ;
; 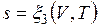 .
.
Значение энтропии для заданного состояния определяется интегрированием уравнения (3.4):

где  — константа интегрирования.
— константа интегрирования.
При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре , стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т. е. s0 = 0 при Т = 0 К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.
Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:
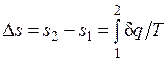 ,
,
поэтому энтропию тоже часто отсчитывают от произвольно выбранного уровня.
Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение (3.3), положив для простоты cv= const:
 . (3.5)
. (3.5)
Из уравнения Клапейрона, записанного для состояний 1 и 2, следует:
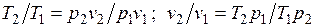 .
.
После подстановки отношений и в выражение (3.4) получим следующие формулы для изменения энтропии идеального газа:
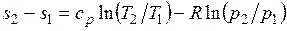 ;
;
 . (3.6)
. (3.6)
Поскольку энтропия есть функция состояния рабочего тела, уравнениями (3.5) — (3.6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

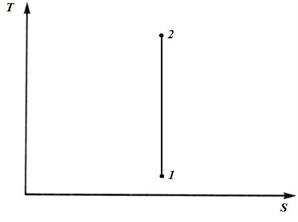
Рисунок 3.2 - Графическое изображение теплоты в T, s – координатах
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов Т, s-диаграмму, на которой (как и на p,v -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (Рисунок 3.2).
В равновесном процессе
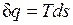 ;
;
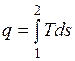 .
.
Очевидно, что в Т, s-диаграмме элементарная теплота процесса  изображается элементарной площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
изображается элементарной площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
Формула 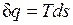 показывает, что ds и
показывает, что ds и  имеют одинаковые знаки, следовательно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу (
имеют одинаковые знаки, следовательно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу (  >0) его энтропия возрастает (ds>0), а при отводе теплоты (
>0) его энтропия возрастает (ds>0), а при отводе теплоты (  <0) — убывает (ds<0).
<0) — убывает (ds<0).
4
0 Теплоемкость – это способность поглощать некоторые объемы тепла во время нагревания или отдавать при охлаждении. Теплоемкость тела – это отношение бесконечно малого числа теплоты, что получает тело, к соответствующему приросту его температурных показателей. Величина измеряется в Дж/К. На практике применяют немного другую величину – удельную теплоемкость.
Теплоемкость тела — это физическая величина, определяемая отношением количества теплоты, поглощенной телом при нагревании, к изменению его температуры:
Физический смысл теплоемкости тела: теплоемкость тела равна количеству теплоты, поглощенному телом при нагревании или выделенному при его охлаждении на 1К.
Теплоемкость тела — это произведение удельной теплоемкости вещества, из которого оно изготовлено, и массы этого тела.
Удельная теплоемкость — это способность разных веществ к поглощению теплоты при их нагревании.
Удельная теплоемкость вещества определяется отношением количества теплоты, полученной им при нагревании, к массе вещества и изменению его температуры, если :
Молярная теплоемкость — это физическая величина, равная отношению количества теплоты, поглощенного веществом при нагревании или выделенного при охлаждении, к количеству молей нем и изменению температуры:
Физический смысл молярной теплоемкости: молярная теплоемкость вещества, определяемая количеством теплоты, которое поглощается при нагревании или выделяется при охлаждении 1 моля вещества на 1 К.
Следовательно, молярную теплоемкость можно определить другим способом:
что говорит о том, что молярная теплоемкость не зависит от его химического состава и температуры.
Уравнение Роберта Майера: молярная теплоемкость идеального газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной:
Закон Дюлонга и Пти: молярная теплоемкость всех теплоемкостей должна быть одинакова и равна утроенной универсальной газовой постоянной:
5
Теплота и работа
Изменение состояния термодинамической системы при ее взаимодействии с внешней средой можно осуществить путем теплообмена или совершением работы.
Процесс передачи энергии системе от внешних тел, называют работой.
Процесс обмена внутренними энергиями соприкасающихся тел, без совершения работы, называют теплообменом.
Количество переданной энергии системе внешними телами путем теплообмена, называют теплотой (количеством теплоты ).
Например, работу над газом, находящимся в цилиндре под поршнем, производят силы давления со стороны внешних сил (рис. 3.1).

Рис. 3.1
Работа А*, совершаемая внешними телами над системой, численно равна и противоположна по знаку работе А, совершаемой системой над внешними телами, т.е. А = - А*.
По определению, давление
Р = Fд / S.
Из механики известно, что работа А* = Fд Dh . Тогда
| А* = Р ( Dh S ) = P DV. | (3.1) |
В процессе совершения работы над системой происходит изменение параметров, характеризующих ее состояние, например, давления, объема, температуры.
Изменить параметры состояния системы можно при теплообмене за счет передачи тепла от одного нагретого тела другому.
Теплота - это не заключенная в теле энергия, а то количество энергии, которое передается от горячего тела холодному.
Таким образом, теплота и работа являются различными формами передачи энергии от одного тела другому. Процессы работы и теплоты качественно различны. Совершение работы над системой может привести к изменению любого вида энергии: кинетической, потенциальной и т.д. Если энергия сообщается системе в форме теплоты, то она идет на увеличение энергии теплового движения частиц системы, называемой внутренней энергией U системы.
Часто оба способа передачи энергии системе могут осуществляться одновременно. Например, при нагревании газа в сосуде с подвижным поршнем. Для перевода системы из одного состояния в другое, с помощью различных термодинамических процессов, ей нужно сообщить различные количества теплоты. Следовательно, теплота и работа, являются функциями процесса изменения состояния системы. Поэтому элементарное количество теплоты, сообщенное системе в процессе бесконечно малого изменения ее состояния, подобно элементарной работе и не является полным дифференциалом.
Полная энергия термодинамической системы включает в себя сумму всех видов энергии частиц, входящих в систему :
1) Кинетическую энергию хаотического движения атомов и молекул (поступательную, вращательную и колебательную энергии).
2) Потенциальную энергию взаимодействия атомов и молекул.
3) Энергию электронных оболочек атомов и ионов.
4) Энергию взаимодействия протонов и нейтронов в ядрах атомов и другие виды энергий.
Во всех процессах, не связанных с химическими реакциями и другими изменениями конфигурации электронных оболочек атомов и ионов, а также с ядерными реакциями в веществах, их энергии не изменяются и не влияют на изменение внутренней энергии.
Внутренняя энергия идеального газа определяется только средней кинетической энергией теплового хаотического движения всех молекул. Изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса перехода, а определяется только параметрами начального и конечного состояний, т.е.
| DU=U2-U1. | (3.2) |
Следовательно, внутренняя энергия является функцией состояния системы.
Работа и теплота зависят от вида процесса перехода системы из состояния 1 в состояние 2. Поэтому работа в тепловых процессах на замкнутом пути не равна нулю. Действительно, пусть система (идеальный газ) переходит из состояния 1 в состояние 2 и обратно в результате двух различных равновесных процессов.
Графически можно изобразить только равновесные процессы.
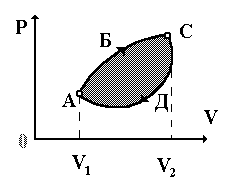
Рис. 3.2
На P - V диаграмме (рис. 3.2) одному из них соответствует кривая А-Б-С. Работа на этом участке
 , ,
| (3.3) |
где давление Р изменяется вдоль кривой А-Б-С.
Работу равна площади криволинейной трапеции, ограниченной сверху кривой А-Б-С.
Другому процессу соответствует кривая А-Д-С, т.е. работа
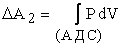 , ,
| (3.4) |
где давление Р изменяется вдоль кривой А-Д-С.
Эта работа равна площади криволинейной трапеции, ограниченной сверху кривой А-Д-С.
Полная работа не равна нулю, т.е.
DА = DА1 - DА2 ¹ 0.
Следовательно, она численно равна площади фигуры, ограниченной кривыми А-Б-С-Д-А.
В чем различие между температурой, теплотой и внутренней энергией?
1. Температура - мера средней кинетической энергии отдельных молекул или мера отклонения системы от термодинамического равновесия.
2. Теплота - количество энергии, переданной от одного тела другому.
Существуют три вида теплообмена: конвекция, излучение, теплопроводность.
а) Излучение - процесс передачи энергии путем теплообмена без совершения механической работы называют излучением.
Для передачи теплоты путем излучения не требуется вещество, как средство передачи теплоты от одного тела другому.
Само существование жизни на Земле возможно только за счет получения энергии от Солнца.
Кванты солнечного света непрерывным потоком устремляются к Земле неся животворную энергию.
На долю Земли приходится около 0,2 % всей энергии излучения Солнца (ежесекундно Земля получает примерно 2 кг фотонов). Остальные 99,8 % энергии излучения Солнца включены во всеобщую галактическую энергию и энергию всей Метагалактики.
Степень поглощения излучения зависит от состояния поверхности и материала тела.
б) Конвекция.
Процесс передачи теплоты за счет перемещения молекул из одной части объема в другую называют конвекцией.
Хотя газы и жидкости являются плохими проводниками теплоты, тем не менее они могут обеспечить довольно быструю передачу ее на значительные расстояния благодаря существованию конвекции. Различают конвекцию естественную и вынужденную.
Например, нагретый атмосферный воздух поднимается вверх, а холодный опускается вниз.
Вблизи батарей радиаторов отопления или других нагревателей нагретый воздух расширяется, его плотность уменьшается, что и приводит к его подъему вверх помещения.
Крупномасштабные проявления естественной конвекции наблюдаются на примере океанских или морских течений (например, Куросиво, Гольфстрим и др.). Ветер - один из примеров явления конвекции, вызывающий изменение погодных условий.
Возникновение конвективных потоков в сосуде с водой при ее нагревании приведены на рис. 3.3.
Рис. 3.3
Теплопроводность будет рассмотрена в разделе "Явления переноса".
3. Внутренняя энергия - полная энергия всех молекул газа [см. п.1.7].
Например, у двух нагретых медных цилиндров равной массы, имеющих одинаковые температуры
внутренняя энергия двух вместе взятых цилиндров будет больше каждого из них в отдельности.
Количество же теплоты передаваться не будет, т.к. температуры одинаковы.
Или, если смешать 100 г воды при температуре 50 0С с 200 г воды при температуре 20 0С, то количество теплоты будет переходить от воды с температурой 50 0С к воде с температурой 20 0С, хотя внутренняя энергия воды при 20 0С больше из-за большей массы.
Энергия (гр. energeia – деятельность) – источник жизни, основа и средство управления всеми природными и общественными системами. Энергия – одно из основных свойств материи – способность производить работу; в широком смысле – сила.
Очевидно, что законы превращения энергии проявляются во всех процессах, происходящих в природе и обществе, включая экономику, культуру, науку и искусство. Энергия – движущая сила мироздания. Компонент энергии есть во всем: в материи, информации, произведениях искусства и человеческом духе.
Фундаментальные законы термодинамики имеют универсальное значение в природе. Любая естественная или искусственная система, не подчиняющаяся этим законам, обречена на гибель. Но для управления энергетическими процессами, прежде всего, необходимо понять роль энергии в экологических системах. Знание закономерностей энергетических потоков в природных экосистемах поможет предсказать будущее антропогенных систем.
Ясно, что будущее зависит от объединения энергетики, экономики и экологии (трех «э») в единую систему взаимосвязанных явлений и процессов. Изучение таких систем требует системного и энергетического подхода, поскольку энергия – это тот фундамент, который позволяет природные ценности перевести в разряд экономических, а экономические – оценивать с позиций экологии.
Природные экологические системы могут служить моделью общих принципов управления, основанного на энергетических процессах. Эти системы существуют на Земле много миллионов лет. Изучив природные системы, можно познать многие законы, справедливые для антропогенных экосистем.
Пища, созданная в результате фотосинтетической деятельности зеленых растений, содержит потенциальную энергию химических связей, которая при потреблении ее животными организмами превращается в другие формы энергии.
Животные, поглощая энергию пищи, большую ее часть переводят в теплоту, а меньшую – в химическую потенциальную энергию.
Энергия существует во многих формах и видах: солнечная, тепловая, химическая, электрическая, атомная, энергия ветра, воды и др. Формы энергии различны по способности производить полезную работу. Энергия слабого ветра, прибоя, маломощных геотермальных источников может произвести небольшое количество работы. Концентрированные формы энергии (нефть, уголь и др.) обладают высоким рабочим потенциалом. Энергия солнечного света по сравнению с энергией ископаемого топлива обладает низкой работоспособностью, а по сравнению с рассеянной низкотемпературной теплотой – высокой. Качество энергии, сконцентрированной в биомассе растений, животных, топливе, отличается от качества рассеянной тепловой энергии.
Качество энергии характеризует ее способность совершать работу, т.е. ее эксергию (гр. ex – высшая степень, ergon – работа).
Эксергия – это максимальная работа, которую совершает термодинамическая система при переходе из данного состояния в состояние физического равновесия с окружающей средой. Эксергией называют полезную долю участвующей в каком-то процессе энергии, значение которой определяется степенью отличия какого-то параметра системы от его значения в окружающей среде.
Для создания энергии более высокого качества необходимы затраты энергии более низкого качества.
Поток солнечной энергии, вовлекаемый в цепь превращений в биосфере, образует порядок и повышает эксергию некоторой части энергии.
Чтобы образовалась 1 ккал биомассы растения, требуется приблизительно в 10 раз меньше килокалорий солнечного света, чем для образования 1 ккал биомассы растительноядного животного. Единица биомассы животного способна совершать работу в соответствующее число раз выше, чем такая же биомасса растений.
В сущности, качество энергии измеряется длиной пути, пройденного ею от Солнца. Энергия высокой концентрации совершает больший объем работы, управляет большим числом процессов. Чтобы сконцентрировать энергию, разные виды ее должны взаимодействовать.
При разработке будущей стратегии в стране и в мире в целом необходимо руководствоваться важнейшим принципом – использовать энергию такого качества, которое соответствует выполняемой работе. Большинство достижений экономики основано на применении многих скрытых косвенных интеллектуальных или дополнительных форм энергии, которые часто не учитываются при оценках стоимости продукции.
Необходимо разрабатывать меры по сохранению, как количества, так и качества энергии.
Сохранение качества энергии – это задача устранения ненужной деградации энергии, ее потерь. Улавливание теплоты с помощью тепловых насосов при производстве электрической энергии – пример энэргосберегающих технологий, препятствующих рассеиванию и потерям энергии. Снижение температуры – энэргоразрушительный процесс, а рециркуляция теплоты – энэргосберегающий.
Энергия – наиболее удобная основа для классификации экосистем. Различают четыре фундаментальных типа экосистем:
1) движимые Солнцем, малосубсидируемые;
2) движимые Солнцем, субсидируемые другими естественными источниками;
3) движимые Солнцем и субсидируемые человеком;
4) движимые топливом.
По мере углубления энергетического кризиса и роста цен на горючее люди, видимо, будут больше интересоваться использованием солнечной энергии и разрабатывать технологии ее концентрации. Возможно, в будущем и возникнет новый тип экосистем – город, движимый энергией не только топлива, но и Солнца.
В своем развитии человеческое общество прошло через все четыре типа описанных выше экосистем.
Чистая энергия – это энергия на выходе из системы в виде продукции после вычета всех энергозатрат на ее преобразования.
Энергию обратной связи (Эш), необходимую для поддержания выхода, иногда называют энергетическим штрафом.
6
Ts-диаграмме
Каждое из этих уравнений содержит два множителя. Один характеризует качество или напряженность энергии (ω2− квадрат скорости, H – высота подъема груза, T – температура, p−давление), а второй – выражает количество или ёмкость тела по отношению к данной энергии (m – масса тела, V− удельный объем, S – энтропия). Первый множитель является интенсивным фактором, а второй – экстенсивным. То есть энтропия представляет собой емкость термодинамической системы по отношению к тепловой напряженности  .
.
Клаузиус дал формулировки первого и второго законов термодинамики.
1. Энергия Вселенной постоянна.
2. Энтропия Вселенной стремится к максимуму.
Таким образом, это должно привести к тепловой смерти Вселенной, когда температура выровняется. Но это противоречит, тому, что закон возрастания энтропии получен для изолированной системы.
TS – диаграмма.
На этой диаграмме по оси ординат откладывается температура, а по оси абсцисс – энтропия.
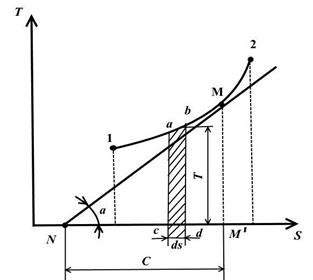
Равновесное состояние в TS− диаграмме изображаются точками с координатами, соответствующими значениям температуры и энтропии.
Обратимый термодинамический процесс изменения состояния рабочего тела от начального состояния 1 до конечного состояния 2 изображается на TS− диаграмме непрерывной кривой, проходящей между этими точками.
Площадь abdc равна TdS=dq, т.е. выражает элементарное количество теплоты, получаемой или отдаваемой системой в обратимом процессе.
Площадь под кривой 1-2 равна
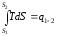 .
.
То есть площадь под кривой в TS− диаграмме, представляет собой теплоту, подведенную к системе или отведенную от нее.
Поэтому TS− диаграмму называют тепловой.
Проведем в произвольной точке M на кривой 1-2 касательную к этой кривой
Величина представляет собой истинную теплоемкость процесса.
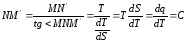
Газовые процессы в TS− диаграмме.
1. Изотермический процесс.
При изотермическом процессе T=const. Поэтому TS− диаграмме он изображается прямой линией, параллельной оси абсцисс.
С учетом того, что dT=0, зависимости изменения энтропии идеального газа в изотермическом процессе примут вид
 (1)
(1)
(уходит слагаемое 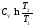 в правой части)
в правой части)
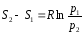 (2)
(2)
Выражение для энтропии идеального газа
 через T,V (1) через T,V (1)
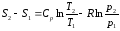 Tp (2) Tp (2)
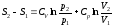 pV (3) pV (3)
|
Процесс 1-2 – это процесс, в котором энтропия увеличивается, а следовательно, к газу подводится теплота и газ совершает работу расширения, эквивалентную этой теплоте.
Процесс2-1− это процесс сжатия, в котором теплота, эквивалентная работе сжатия, отводится от газа и энтропия уменьшается
Площадь фигуры S112 S2 соответствует количеству теплоты q, сообщаемому газу, и одновременно работе l (изотермический процесс)
2. Адиабатный процесс
В адиабатном процессе q=0 и dq=0, а следовательно dS=0.
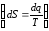
Следовательно, в адиабатном процессе S=const и в TS − диаграмме адиабатный процесс изображается прямой линией, параллельной оси T.
Поскольку в адиабатном процессе S=const,то адиабатные обратимые процессы называют также изоэнтропными.
При адиабатном сжатии температура рабочего тела повышается, а при расширении понижается. Поэтому процесс1-2 – это процесс сжатия, а процесс 2-1 – это расширение.
Из уравнения
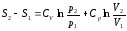 (3)
(3)
При k=const получим 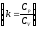

или
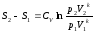 (*)
(*)
Для обратимого адиабатного процесса S1=S2=const, тогда из (*)
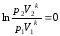
Откуда,
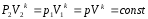
− уравнение адиабаты в координатах p и V.
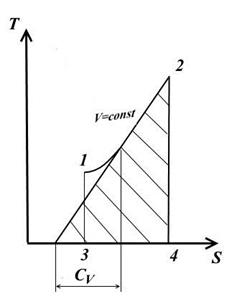
3. Изохорный процесс
Для изохорного процесса V=const, dV=0.
При постоянной теплоемкости (из ур. (1))
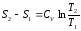 −вид на TS – диаграмме
−вид на TS – диаграмме
Подкасательная к кривой процесса в любой её точке определяет значение истинной теплоёмкости CV.
Подкасательная будет положительной только в том случае, если кривая будет обращена выпуклостью вниз.
Площадь под кривой процесса 1-2 на TS – диаграмме дает в масштабе количество подведенной (или отведенной в процессе 2-1) теплоты q, равное изменению внутренней энергии U2-U1.
4. Изобарный процесс
В изобарном процессе давление постоянное p=const
В этом случае
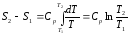 из (2)
из (2)
Следовательно, при p=const как и при V=const изобара является логарифмической кривой, поднимается следа направо и обращена выпуклостью вниз.
Подкасательная к кривой 1-2 в любой её точке дает значения истинной теплоёмкости Cp.
Площадь под кривой дает кол-во теплоты q, которая сообщается газу при p=const, равное изменению энтальпии i2-i1.
5. Политропный процесс
В политропном процессе 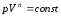 .Теплоёмкость в этом процессе
.Теплоёмкость в этом процессе
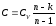
Тогда,
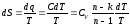
Отсюда, для конечного изменения состояния газа
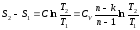
Политропный процесс на TS – диаграмме изображается кривой, расположение которой зависит от показателя n.
6. Круговой процесс. Цикл Карно.
Изобразим в TS – диаграмме произвольный обратимый цикл 1a2b1.
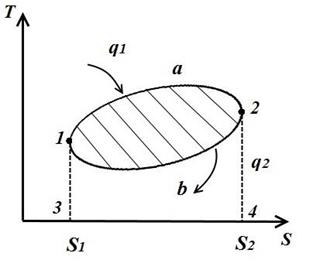
В процессе 1a2 рабочее тело получает кол-во теплоты q1, численно равное площади под кривой 1a2, а в процессе 2-b-1 отдает кол-во теплоты q2, численно равное площади под кривой 2-b-1.
Часть теплоты
переходит в работу цикла l (∆u=0 в цикле).
Работа цикла положительна, если цикл проходит по часовой стрелке и отрицательна, если против часовой стрелки (направление цикла в pV и TS − диаграммах одинакова).
Термический к.п.д. кругового процесса
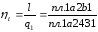
Изменение энтропии в любом цикле равно нулю.
Цикл Карно состоит из двух изотерм и двух адиабат. В TS – диаграмме он будет изображаться в виде прямоугольника (горизонтальные линии – изотермы, вертикальные – адиабаты)
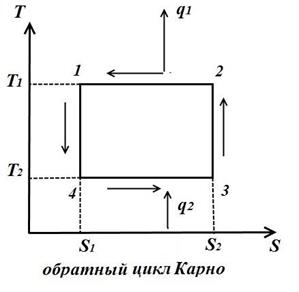
Количество теплоты, подведенное к рабочему телу, числено равно площади прямоугольника 12S2S1:
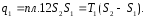
Количество теплоты, отведенное к холодильнику, соответствует площади прямоугольника 34S1S2:
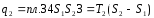
Теплота, эквивалентная работе цикла, равная площади цикла

Термический к.п.д. цикла
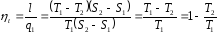
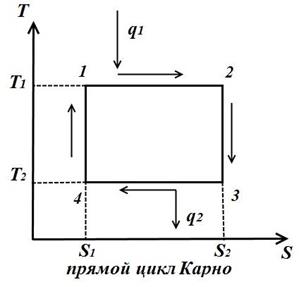
Для обратного цикла (рис. справа)
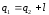
Холодильный коэффициент обратного цикла
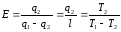
Горение твердого топлива
Твердое топливо является термически нестойким органическим веществом, процесс горения которого протекает через ряд стадий. Основной стадией, определяющей интенсивность всего процесса в целом, является стадия горения так называемого коксового остатка — углерода, оставшегося в частице топлива после завершения деструкции вещества исходного топлива и выхода летучих веществ. В основе процесса горения частиц углерода лежат гетерогенные химические реакции взаимодействия углерода с окружающими горящую частицу газами: 02, Н20, С02 и др. Наиболее глубокие исследования горения углерода проведены в СССР А. С. Предводителевым, Л. Н. Хитриным, Г. Ф. Кнорре, Б. В. Канторовичем и др.
В основе процесса горения частицы углерода, движущейся в потоке воздуха, лежит модель, предложенная Л. Н. Хитриным, согласно которой угольные частицы малых размеров приобретают скорость, близкую к скоростям движения потока воздуха. При таком условии вынужденный конвективный перенос массы отсутствует и частица выгорает равномерно. При этом возможны четыре режима взаимодействия углерода с кислородом воздуха в зависимости от температуры среды (рис. 2.14). Основными реакциями в модели считаются реакции углерода с кислородом, поступающим к поверхности частицы за счет диффузии из основного потока с образованием оксида и диоксида углерода. Продукты сгорания диффундируют от поверхности частицы в окружающее ее пространство. При невысоких температурах (973 К) (реакция 1) реакции окисления углерода протекают с образованием СО и СОг. При более высоких температурах (1070—1470 К) возможна вторичная реакция догорания образовавшегося СО вблизи поверхности частицы так, что в окружающую среду будет отводиться только или преимущественно диоксид углерода (СОг) (реакция 1). При этом часть образовавшегося СОг может при Т = = 1473—1573 К вновь продиффундировать к поверхности углерода и вступить с ним в эндотермическую реакцию с образованием оксида углерода (реакция 2), который затем догорит в результате взаимодействия с кислородом в зоне пламени вокруг частицы.

При высоких температурах (выше 1470—1570 К), как правило, кислород не достигает поверхности частицы и процесс горения протекает по гетерогенной реакции С+ +С02 = 2С0 С последующим догоранием СО на некотором расстоянии от поверхности в зоне пламени (реакция 2). В случае омывания частицы потоком окислителя с большой скоростью (Re>100) с лобовой стороны частицы будут протекать только гетерогенные реакции (реакции 1 и 2, рис. 2.14,6); догорание же оксида углерода будет наблюдаться в кормовой части потока на границе циркуляционной зоны (реакция 3, рис. 2.14,6), а вторичные реакции C-f-C02 будут иметь место главным образом в тыльной части углеродной частицы (схема 2, рис. 2.14,6), где кислород отсутствует, но имеются хорошие тепловые условия для обеспечения эндотермических реакций.
Важной отличительной особенностью горения коксового (углеродного) остатка частицы твердого топлива является его высокая пористость, что обеспечивает диффузию внутрь углеродной частицы активных по отношению к углероду газов (С02, 02, Н20). Л. Н. Хитрин оценивает величину удельной внутренней поверхности частицы, приходящейся на единицу ее объема, для древесного угля от 57 до 114 см2/см3, для электродного угля от 70 до 500 и для антрацита около 1000 см2/см3. В ходе реагирования внутренняя поверхность частицы увеличивается за счет испарения влаги, выхода летучих веществ, изменения температуры и других факторов.
Чем больше проницаемость материала, интенсивнее диффузия газов внутрь его и чем медленнее протекает реакция, тем глубже проникание кислорода и других газов внутрь частицы и тем большая масса участвует в реакции. Процесс внутренней диффузии можно рассматривать как самостоятельный, не зависящий от характера диффузионных процессов в зоне горения: В этом случае суммарную скорость гетерогенной реакции через потребление кислорода можно записать (согласно Л. Н. Хит- рину):
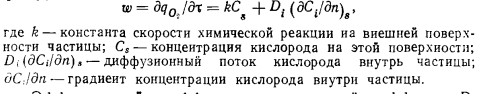
Эффективный коэффициент внутренней диффузии Д зависит от пористости материала, величины и свойств поверхности пор. Величина внутридиффузионного потока зависит от проницаемости материала и интенсивности реагирования на поверхности его пор. Она определяется значениями кинетических констант и размером внутренней реакционной поверхности в единице объема частицы. Чем выше активность и воспламеняемость твердого топлива и чем при меньших температурах оно воспламеняется, тем в меньшей степени увеличивается его внутренняя поверхность во время его термической деструкции на начальных стадиях горения и тем меньшее значение в процессе имеет внутреннее реагирование. И, наоборот, чем менее реакционное топливо, чем труднее оно воспламеняется, тем процессы, приводящие к раскрытию пор угольного вещества, протекают полнее и тем выше значение внутреннего реагирования.
Особенно значительна роль внутреннего реагирования при горении композиционных топлив — топливных гранул, капель топливных суспензий и др. С повышением температуры горения значение внутреннего реагирования ослабевает. При сжигании высокозольных твердых топлив даже при высоких температурах значение внутреннего реагирования существенно возрастает, так как зольная оболочка, образующаяся при выгорании такой частицы, становится дополнительным сопротивлением для диффузии газов к поверхности реагирования. Однако влияние этой оболочки на процесс сказывается только при горении крупных частиц топлива; при пылевидном сжигании даже при зольности топлива 30—35 % это влияние несущественно.
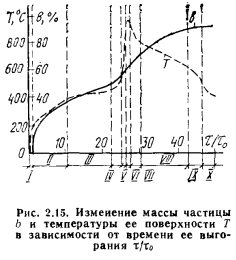
При горении частицы натурального твердого топлива стадии горения коксового (углеродного) остатка предшествует ряд факторов, существенно влияющих на процесс в целом, а именно: подогрев и подсушка частицы топлива; деструкция вещества топлива с выделением летучих; горение летучих и др. Важной особенностью горения этих частиц является четко выраженная стадийность с резким изменением характера закономерностей развития каждой стадии во времени. Экспериментальные исследования динамики выгорания частицы твердого топлива (рис. 2.15), выполненные практически на всех марках угля в широком диапазоне температур среды (от 573 до 1273 К), позволили создать модель горения частицы натурального топлива — угля, включающую 10, а для высоковлажных углей и водоугольных суспензий — 11 стадий процесса.
При вводе частицы в высокотемпературную окислительную среду она вначале проходит стадию прогрева I при определяющем влиянии внешнего теплообмена и массопереноса на изменение массы и температуры частицы. При выгорании частицы высоковлажного топлива или капли водоугольной суспензии вслед за стадией прогрева наблюдается стадия поверхностного испарения влаги (на схеме не показана), протекающая при постоянной температуре частицы. Собственно процесс горения частицы начинается со стадии II— стадии дальнейшего прогрева частицы и начала низкотемпературных экзотермических реакций внутри объема частицы, что приводит к достаточно резкому увеличению ее температуры при непрерывной скорости изменения температуры и потери массы.
Стадия III характерна уменьшением скорости роста температур в связи с началом эндотермических реакций деструкции угольного вещества с выходом летучих продуктов этой деструкции. Стадия завершается воспламенением летучих вокруг частицы, что приводит к интенсификации процессов деструкции внутри частицы. Эти процессы продолжаются во время IV стадии — стадии горения летучих; V—стадия параллельного протекания процессов горения летучих вокруг объема частицы и начала поверхностного гетерогенного горения углерода, о чем свидетельствует резкое возрастание температуры поверхности частицы; VI — стадия активного поверхностного горения с догоранием вокруг поверхности еще выделяющихся летучих. Во время этой стадии достигается максимальная температура поверхности частицы.
Во время I—V стадий происходит изменение структуры реагирующей частицы с резким увеличением ее пористости и активации открывающейся поверхности. На стадии VII наблюдается активное горение коксового (углеродного) остатка частицы с догоранием еще выделяющихся летучих на ее поверхности. Эта стадия характеризуется резким падением температуры на поверхности частицы. VIII стадия — это горение коксового остатка, как правило, самая продолжительная стадия, протекающая при плавном снижении температуры поверхности и развитии реакций внутри объема частицы. Процесс горения заканчивается стадией догорания коксового остатка (стадия IX), в основе которой лежит внутреннее реагирование углерода частицы с диффундирующими внутрь ее газами, и стадией X — стадией охлаждения зольного остатка частицы до температуры среды. Важно, что практически все стадии протекают при разных режимах горения от чисто диффузионных (стадии I, II. IV, VII, VIII, IX) до кинетических (стадии III, VI).
В целом же весь процесс выгорания частицы натурального твердого топлива суммарно можно рассматривать как протекающий в промежуточном режиме ближе к диффузионному, а для инженерных расчетов — в чисто диффузионном режиме. При термической деструкции угольного вещества (стадии II, III, IV, V) происходит выделение продуктов деструкции в виде газа, кислоты, воды и смолы. Относительная доля выделяющихся газа и жидкости зависит от скорости нагрева частицы: чем выше скорость нагрева, тем выход этих веществ больше. По мере движения к поверхности частицы вода и кислоты испаряются, а смола и газообразные углеводороды подвергаются вторичному разложению. Водяной пар, проходя через раскаленную углеродную поверхность, на стадиях IV и V может вступать в реакцию с углеродом и интенсифицировать процесс.
В конце III стадии процесса происходит воспламенение частицы топлива, которое практически во всех случаях начинается с воспламенения выделившихся из нее горючих летучих, имеющих более низкую температуру воспламенения, чем коксовый (углеродный) ее остаток. В связи с этим роль летучих в процессе воспламенения во многом является решающей. Выход летучих является следствием деструкции угольного вещества; чем выше интенсивность их выхода, тем больше глубина деструкции, прямым следствием которой является активация образующейся новой реакционной поверхности твердого остатка за счет повышения пористости частицы. Образование летучих в объеме частицы приводит к повышению ее внутреннего давления и к разработке поверхности твердого остатка, что способствует существенной интенсификации процесса горения в целом, особенно на заключительной его стадии.
В то же время выделяющиеся летучие обволакивают частицу и при определенных условиях на стадии IV и V (частично) препятствуют диффузии кислорода к поверхности частицы и тем самым в известной степени несколько тормозят основные гетерогенные реакции горения. Однако, как показали исследования, это наблюдается только у относительно крупной частицы размером 1,0 мм и более. Чем выше размер частицы, тем относительно меньшая доля летучих выделяется до момента их воспламенения и тем большая их часть выгорает параллельно с гетерогенным реагированием на поверхности частицы.
При сжигании частиц топлива в потоке большое значение в процессе воспламенения играет время индукции Тинд, т. е. время, затрачиваемое на самопроизвольное повышение температуры в процессе химического реагирования горючего с окислителем, приводящего к воспламенению. Величина тИнД определяется как промежуток времени, в течение которого температура частицы повышается от начальной до температуры воспламенения. Чем выше температура среды, в которую введена частица топлива, тем меньше время индукции. Для оценки процесса воспламенения твердых топлив иногда пользуются параметром условная температура воспламенения— минимальная температура среды, при которой происходит воспламенение частицы при длительном ее пребывании в ней (т. е. при ТцНд 0). Эта температура воспламенения зависит не только от вида топлива, но и от тепловых условий взаимодействия частицы со средой. Так, для одиночной мелкой частицы эта температура меняется от 1170—1270 К для антрацита до 800—850 К для бурого угля. Для частиц тех же топлив, находящихся в контакте с другими такими же частицами (например, в слое), эта температура снижается почти в 2 раза, что свидетельствует о более благоприятных условиях воспламенения топлива при слоевом его сжигании.
При инженерных расчетах времени горения частицы твердого топлива стадии горения условно объединяют в четыре укрупненные расчетные стадии (см. рис. 2.15):
1) от момента ввода частицы в зону горения до момента воспламенения летучих (стадии /, II и III); время этой стадии рассчитывают как время выхода летучих твл
2) от момента воспламенения летучих до конца их видимого горения (стадии IV, V); время этой стадии рассчитывают как время видимого горения летучих тгл; 3) от момента прекращения видимого горения летучих до начала активного горения коксового остатка (стадия VI); время стадии рассчитывают как время прогрева коксового остатка до его воспламенения твл; 4) от момента начала активного горения коксового остатка до завершения процесса (стадии VII, VIII, IX); время стадии рассчитывают как время горения коксового остатка тГк).
Эти условные времена расчетных стадий горения частицы рассчитывают на основании экспериментальных данных, полученных при изучении изменения цветовой температуры частицы в процессе горения, а также визуального наблюдения за процессом с применением киносъемки. Расчетные зависимости позволяют определить влияние начального размера частицы d, мм; температуры среды Гг, К; концентрации кислорода 02, %; плотности частицы рчт, кг/м3, на время протекания расчетных стадий процесса. При этом принято, что
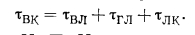
В. И. Бабий и И. П. Иванова получили следующие эмпирические зависимости для времен расчетных стадий процесса:
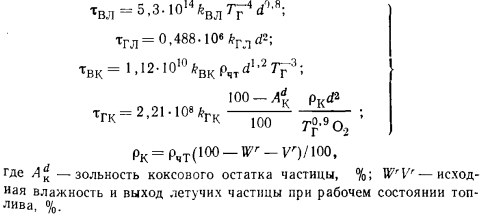
Коэффициенты k в формулах суммарно характеризуют физико-химические свойства исходных топлив и получены экспериментально. Для углей (бурых, каменных и антрацитов) значения k меняются в пределах: &Вл — от 0.82 до 1,06; 6ГЛ — от 1,00 до 1,42; kBK — от 0,8 до 1,59;. гк — от 0,45 до 1,02. Анализ формул показывает, что расчетная стадия выхода летучих, определяемая твл,- пропорциональна интенсивности теплового излучения на поверхность капли (твлГ4) н время ее протекания практически линейно зависит от диаметра частицы (тВл~08), что свидетельствует об участии всей массы частицы в этом процессе.
Время расчетной стадии горения летучих (2—3) определяется только величиной поверхности частицы топлива (тлг~2), поскольку горение летучих протекает вокруг частицы и не зависит ни от температуры среды, ни от других параметров. Время протекания расчетной стадии горения коксового остатка тГк линейно зависит от концентрации кислорода (что свидетельствует о первом порядке реакции), пропорционально поверхности частицы d2 (это означает, что относительно малая роль внутреннего реагирования) и слабо зависит от температуры среды ТгкГ-09 (что является следствием преимущественно диффузионного режима горения). Приведенные формулы позволяют получить сравнительные данные о поведении частиц углей различных марок при их выгорании.
Горение жидкого топлива
Жидкое топливо в топочных устройствах, как правило, сжигается в распыленном состоянии, в виде капель в потоке воздуха. Горение жидких топлив всегда происходит в паровой фазе, поэтому процессу горения капли всегда предшествует процесс испарения. В общем случае в высокотемпературной среде капля жидкого топлива окружена некоторой зоной, насыщенной его парами, на внешней поверхности которой вокруг капли устанавливается сферическая зона горения. Скорость химической реакции смеси паров жидкого топлива с окислителем достаточно велика, так что толщина зоны горения по отношению к диаметру зоны горения незначительна. Толщина паровой зоны вокруг капли топлива зависит от температуры в зоне горения и от параметров испарения топлива: чем выше температура горения и чем ниже температура кипения топлива и теплота его испарения, тем выше толщина паровой зоны.
В стационарном процессе скорость горения жидкого топлива в случае, если все оно выгорает в зоне вокруг капли, зависит от скорости его испарения. В пространстве между зоной горения и каплей находятся пары топлива и некоторая часть продиффундировавших туда продуктов сгорания, а вне зоны горения — окислитель и продукты сгорания (рис. 2.16). В зону горения из объема капли диффундируют пары топлива, а с внешней стороны — окислитель (кислород воздуха). В результате реакции с выделением теплоты образуются продукты сгорания, которые в основном отводятся в окружающее каплю пространство.
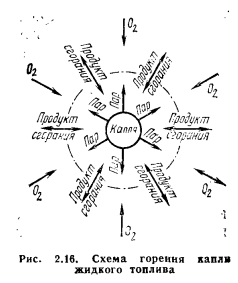
Теплота, необходимая для испарения топлива, передается поверхности капли из зоны горения в основном излучением и в результате частичной диффузии внутрь паровой оболочки продуктов сгорания. При таких предпосылках время горения капли жидкого топлива в диффузионном режиме может быть рассчитано на основании теплового баланса ее испарения
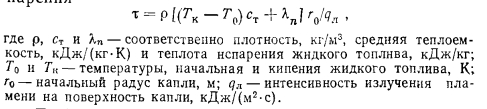
Любое жидкое топливо, в том числе дизельное топливо и мазут, полученное из нефти путем ее разделения по температурам кипения отдельных фракций, содержит ряд индивидуальных углеводородов со своей температурой кипения. Поэтому процесс горения капель такого топлива протекает сложнее и в инженерных расчетах время выгорания капли топлива рассчитывают, используя соотношение, вытекающее из линейной зависимости квадрата диаметра капли топлива от времени т его испарения (закон Срезневского):
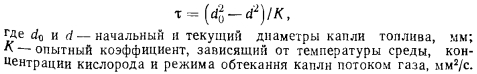
При горении в воздухе с температурой 1070—1170 К и скоростях обтекания капли до 1 м/с для мазута и солярового масла величина /С=1-у1,2 мм2/с. При очень Малых размерах капель и высоких скоростях обтекания возможны режимы, при которых пары топлива выносятся в потоке газов и сгорают там по законам газовых смесей. Для обеспечения необходимой интенсивности испарения жидких топлив и их перемешивания с окислителем при вводе в зону горения они распыляются в потоке воздуха с образованием полидисперсного потока мелких капель размерами от 0 до 0,15—0,2 мм. Этим достигается большая удельная поверхность испарения, а затем и горения. Мелкие капли топлива быстро испаряются н создают газовоздушную смесь, которая, воспламеняясь, образует горящий факел. Область распространения факела можно условно разделить на следующие зоны: распыления топлива, его испарения и образования газовоздушной смеси, воспламенения и горения этой смеси. Как по сечению топливно-воздушной струи, так и по ее длине в процессе горения непрерывно изменяются температура и концентрация топлива и окислителя. При этом возможно образование локальных зон, в которых концентрация топлива будет выше теоретически необходимой. Не допустить образования таких зон — значит обеспечить высокую полноту выгорания жидкого топлива.
Для производства тепловой энергии из нефтяных топлив применяют лишь мазут и печное бытовое топливо. При сжигании мазута для испарения его наиболее тяжелых фракций с температурой кипения 700 К и выше требуется прогрев капель до таких температур, при которых происходит деструкция топлива с образованием как газообразной, так и твердой фазы. Таким образом, при нагреве капель мазута до высокой температуры образуется твердая углеродная фаза — сажа и кокс, которые выгорают так же, как частицы твердого топлива, но имеют значительно меньшую активность по отношению к кислороду воздуха. Раскаленные частицы сажи и кокса в пламени обусловливают светимость факела. Газообразные и твердые продукты разложения мазута, выделяющиеся в зоне, в которой концентрация кислорода уже невелика, образуют зону догорания топлива, существенно увеличивающую общую длину факела.
31. Горение газа
Горение газов осуществляется в объеме и относится к гомогенному горению; оно может происходить в кинетической и диффузионных областях.
Кинетическое горение
После того как произошло воспламенение, наступает процесс распространения пламени, связанный с постоянной передачей тепла от сгоревших к новым порциям топлива. Подобная передача тепла определяется законами теплопроводности и диффузии и зависит от характера пламени. Если пламя распространяется в неподвижной смеси или в смеси, движущейся ламинарно, то основной формой передачи тепла является молекулярная теплопроводность.Подобный чисто теплопроводный процесс получил название нормального горения. При турбулентном движении газоокислительной смеси большую роль приобретает турбулентная диффузия. При некоторых условиях распространение пламени происходит с огромной скоростью и имеет характер взрывной волны. Подобное распространение пламени получило название детонационного горения или просто детонации.
Нормальное горение. После воспламенения горючей смеси возникает определенный фронт горения. Распространение пламени предполагает перемещение этого горения в направлении несгоревших порций газа. Позади фронта горения находятся продукты сгорания, впереди — невоспламенившаяся горючая смесь
Возникшая при этом разность температур между продуктами сгорания и горючей смесью приводит к передаче тепла теплопроводностью, которая, опережая фронт горения, способствует подогреву новых порций смеси до температуры воспламенения и вызывает перемещение фронта. В большинстве случаев при горении газов фронт пламенч является очень тонким —около 4×10–2 —6×10–2 см, поэтому с некоторым приближением его можно рассматривать как поверхность.При нормальном горении фронт пламени в покоящейся горючей смеси перемещается с определенной скоростью un = Dn/Dt, где Dn — расстояние, на которое перемещается фронт пламени за время Dt.Скорость нормального горения определяется исключительно процессом теплопроводности и потому является физико-химической константой горючей смеси.По современным представлениям горение газовой смеси может быть изображено графически (рис. 43). Самовоспламенение происходит в точке Tв, но до идет химическая реакция, свойственная индукционному периоду. Быстрая реакция происходит в коротком интервале температур от в до Тг, который соответствует химической толщине фронта пламени dр.Тепловая толщина фронта бп представляет собой зону тепловой подготовки прогрева горючей смеси до , после которой развивается интенсивная химическая реакция.
Для всех горючих газов существует оптимальное соотношение газа и воздуха, при котором скорость нормального горения достигает максимальной величины.
Увеличение температуры подогрева газа или газовой: смеси приводит к существенному увеличению скорости горения.
Горение однородной смеси в турбулентном потоке. Горение при турбулентном режиме — гораздо более распространенный случай в металлургической практике по сравнению с горением в спокойной или ламинарно движущейся среде.
В настоящее время турбулентное горение рассматривается как процесс, протекающий в отдельных перемешивающихся объемах (объемное горение).
На скорость турбулентного горения и на состояние фронта горения большое влияние оказывает общий уровень турбулентности потока. Измерения скорости турбулентного перемещения пламени показали, что отношение скорости турбулентного распространения пламени к нормальной скорости uт/uн быстро возрастает с увеличением числа Rе.
Это увеличение происходит в результате изменения uт, так как uн — const.
Диффузионное горение
В настоящее время широко распространен диффузионный метод сжигания газообразного топлива, при котором смешение и горение происходит в одном объеме. Поэтому процессы смешения при диффузионном горении играют первостепенную роль.
Процессы смешения между струями топлива и воздуха могут протекать при ламинарном и турбулентном течениях этих струй. В первом случае смешение определяется молекулярной диффузией, во втором — турбулентной диффузией.На рис. 44 представлена упрощенная схема распределения концентраций в ламинарном пламени. Как видно, кислород полностью отсутствует внутри объема, ограниченного фронтом пламени, так же как топливо отсутствует за пределами этого объема.Расчеты и опыты показали, что высота пламени пропорциональна скорости подачи газа и обратно пропорциональна коэффициенту диффузии.Если рассматривать факел, образующийся при вытекании горючего газа в неограниченную спокойную среду, то при определенной (критической) скорости ламинарный факел начнет переходить в турбулентный.
Критическое значение критерия Rекр, при достижении которого начинается переход ламинарного пламени в турбулентное, зависит от вида топлива, динамических характеристик потока и влияния на них процесса горения.
32
Циклы компрессоров
5.6.1. Способы получения высоких давлений газов
Сжатые газы широко используются в сельскохозяйственном производстве как в качестве энергоносителей, так и рабочего тела в различных технологических процессах. Машины для создания давления и подачи газа потребителю называют в е н т и л я т о р а м и, в о з д у х о д у в к а м и, к о- м п р е с с о р а м и. Компрессоры создают избыточное давление от 0,15 МПа
.и более; нагнетатели и насосы – от 0.02 до 0.2 МПа; вентиляторы повышают давление газов до 0,02 МПа.
По принципу действия компрессоры делятся на две группы: объемные и динамические.
В объемных компрессорах повышение давления достигается сжатием газа путем сближения ограничивающих его стенок. Объемные компрессоры подразделяются на поршневые, ротационные, винтовые и мембранные.
В динамических компрессорах газу первоначально сообщается некоторая кинетическая энергия, которая затем в специальных каналах (диффузорах) преобразуется в потенциальную энергию давления. Динамические компрессоры
компрессоры подразделяются на лопаточные и струйные.
Н  а рис. 5.15 представлена схема поршневого одноступенчатого охлаждаемого компрессора. В цилиндре 1 поршень 2 перемещается кривошипно- шатунным механизмом При движении поршня слева направо открывается впускной клапан 3 и цилиндр заполняется газом. При обратном движении поршня впускной клапан закрывается, объем газа в ци- линдре уменьшается, а давление увеличивается. Давление на выходе из компрессора устанав- ливается регулировкой выпускного клапана 4.При открытии последнего газ выталкивается поршнем из цилиндра и подается потребителю с давлением нагнетания. С целью снижения энер-
а рис. 5.15 представлена схема поршневого одноступенчатого охлаждаемого компрессора. В цилиндре 1 поршень 2 перемещается кривошипно- шатунным механизмом При движении поршня слева направо открывается впускной клапан 3 и цилиндр заполняется газом. При обратном движении поршня впускной клапан закрывается, объем газа в ци- линдре уменьшается, а давление увеличивается. Давление на выходе из компрессора устанав- ливается регулировкой выпускного клапана 4.При открытии последнего газ выталкивается поршнем из цилиндра и подается потребителю с давлением нагнетания. С целью снижения энер-
Рис. 5.15 гии, затрачиваемой на сжатие газа, цилиндр охлаждается теплоносителем 5.
Схема ротационного компрессора показана на рис.5.16. В корпусе 1
эксцентрично расположен ротор 3, в пазах которого свободно скользят пластины 2. При вращении ротора под действием центробежных сил пластины плотно прижимаются к корпусу, препятствуя перетеканию газа из одной полости в другую. Попавшая между пластинами порция газа по ходу вращения ротора уменьшается в объеме, за счет чего и повышается давление.
Н  а рис. 5.17 представлена схема винтового компрессора. В корпусе 3 на подшипниках 1 и 4 установлены два ротора:
а рис. 5.17 представлена схема винтового компрессора. В корпусе 3 на подшипниках 1 и 4 установлены два ротора:
Рис. 5.16ведущий 7 и ведомый 6. Для предотвра
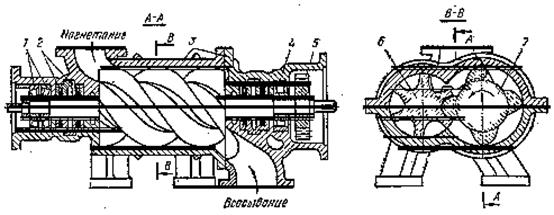
Рис. 5.17
щения утечки газов по валам роторов установлены специальные уплотнения 2. Синхронное вращение роторов обеспечивается шестернями связи 5. В корпусе имеются патрубки для всасывания и нагнетания газа с окнами против торцов роторов. По мере того как роторы делают один оборот, всасывающее окно перекрывается зубьями, а поступившая порция газа, перемещаясь вдоль роторов. Зубья ведущего ротора входят в соответствующие углубления в ведомом роторе, в результате чего объем газа уменьшается, а давление увеличивается. К противоположному торцу роторов газ поступает в сжатом состоянии и выталкивается в нагнетательное окно.
Схемы лопаточных компрессоров приведены на рис 5.18 и рис. 5.19
В корпусе 1 центробежного компрессора (см. рис.5.18) вращается диск 2,
выполненный с рабочими лопатками в виде каналов 3. Газ, поступивший в
1. 

Назначение и
2.
3.
4.
Рис. 5.18 Рис. 5.19
межлопаточные каналы, отбрасывается центробежными силами к периферии и попадает в диффузоры 4, лопатки которых укреплены в корпусе. В диффузорах происходит преобразование кинетической энергии газа в потенциальную энергию давления. Через нагнетательный патрубок сжатый газ поступает потребителю.
В осевом компрессоре (см. рис.5.19) направление движения газа
совпадает с осью ротора. Рабочие лопатки компрессора 1 закреплены в кольцевых проточках ротора 6, образуя форму дисков. Осевое расстояние между дисками обеспечивает размещение в корпусе 5 лопаток 2 спрямляющего аппарата, выполняющего роль диффузора. Канал, образованный лопатками одного диска и последующего за ним спрямляющего аппарата, называют с т у-п е н ь ю компрессора. Спрямляющие лопатки первого ряда 3 и конффузор 4 обеспечивают осевое направление входящего в компрессор воздуха. При вращении ротора кинетическая энергия газа в каналах между рабочими лопатками становится существенной. Газовый поток, проходя далее диффу-
зор 7, преобразует. кинетическую энергию в энергию сил давления. Давление на выходе из компрессора в основном определяется количеством ступеней.
К показателям компрессорных машин относят:
- тип компрессора;
- число ступеней, z;
- степень повышения давления в компрессора, 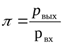 ;
;
- подачу компрессора,  м3/с .
м3/с .
Под объемной подачей понимают количество кубических метров газа, выходящего из компрессора в единицу времени и приведенного к давлению и температуре на входе в компрессор.
На рис. 5.20 показаны поля применимости компрессоров
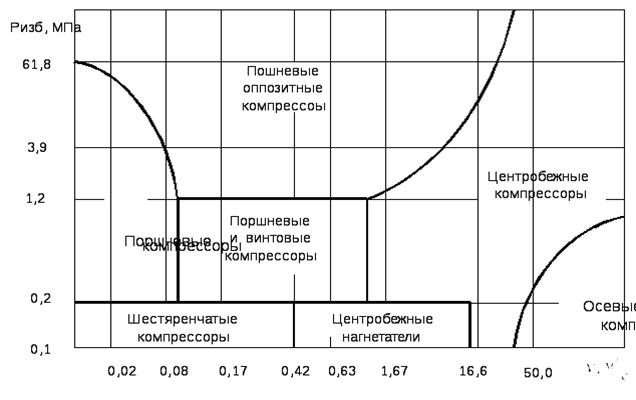 Рис. 5.20
Рис. 5.20
5.6.2. Поршневой компрессор и его показатели
В одноступенчатом поршневом компрессоре (ОПК) зависимость давления газа внутри цилиндра от занимаемого им объема определяют опытным путем с помощью прибора, именуемого и н д и к а т о р о м. Подобную зависимость, например, изображенную на рис. 5.21, называют и н д и к а т о р- н о й д и а г р а м м о й или действительным циклом ОПК.
Рассмотрим процессы этого цикла.
4-1 – процесс наполнения цилиндра «свежей» порцией газа. Этот процесс не является термодинамическим, так как он осуществляется с нарастанием массы газа, практически с неизменной температурой и переменным давлением;
1-2 – процесс повышения давления. В этом процессе на начальном этапе к газу от стенок цилиндра подводится тепло, а в конце сжатия, наоборот, газ нагревает стенки. Данный процесс необратим;
2-3 – процесс нагнетания. Он протекает с изменением массы газа,
с  забросом давления для открытия выпускного клапана и неизменной температурой. Этот процесс тоже далек от термодинамического;
забросом давления для открытия выпускного клапана и неизменной температурой. Этот процесс тоже далек от термодинамического;
3-4 – процесс расширения газа, оставшегося в цилиндре после закрытия. Этому процессу присущи как подвод, так и отвод тепла.
В реальном поршневом компрессоре при нагнетании не весь газ покидает цилиндр. Часть его остается в объеме так называемого в р е д н о г о пространства V0 (объем между крышкой цилиндра и крайним левым положением поршня). При движении поршня слева направо оставшийся в цилиндре газ расширяется, Рис. 5.21
занимая объем V4 . Объем новой всасываемой порции газа будет равен только разности: Vвс = V1– V4.
К показателям поршневого компрессора, кроме степени повышения давления  и объемной подачи
и объемной подачи 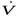 , относят:
, относят:
– величину рабочего объема цилиндра Vp, м3;
– относительную величину вредного объема 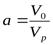 ;
;
– коэффициент объемной подачи 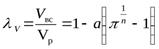 .
.
С увеличением 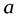 и
и 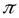 объемная подача поршневого компрессора
объемная подача поршневого компрессора
уменьшается, что наглядно демонстрируется рисунками 5.22 и 5.23.

Рис.5.22 Рис. 5.23
Величина вредного пространства ограничивает и давление нагнетания ОПК. Так при λ = 0 значение 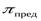 определяется по выражению:
определяется по выражению:
 .
.
Степень повышения давления у реальных компрессоров лимитируется не только относительной величиной вредного пространства, но и температурой газа в конце сжатия T2, которая не должна превышать температур самовоспламенения смазки. В одноступенчатом компрессоре с учетом реальных значений  ,
, 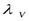 иT2 можно получить
иT2 можно получить 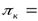 3,75… 4,25. В современных поршневых компрессорах
3,75… 4,25. В современных поршневых компрессорах 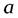 = 0,025…0,045 и
= 0,025…0,045 и 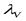 = 0,75…090.
= 0,75…090.
Для оценки совершенства реального компрессора проводят анализ его идеального цикла.
5.6.3. Идеальный цикл одноступенчатого поршневого компрессора
Заменим реальный цикл компрессора идеальным, для чего примем допущения:
– вредное пространство в компрессоре отсутствует;
– процессы всасывания и нагнетания, протекающие с изменением
массы газа, считаем термодинамическими;
– тепловые и механические потери отсутствуют.
. На рис. 5.24 идеальный цикл ОПК изображен в pV-координатах , а на рис.5.25, – в Ts – координатах.
Рис. 5.24 Рис. 5.25
В принципе, процесс сжатия может быть изотермическим (1-2), адиабатным (1-2¢¢) или политропным с n< к (1-2¢) и n > к (1-2```). Процесс нагнетания сжатого газа (2-3) осуществляется изобарно. Процесс (3-4) – условный, соответствует падению давления в цилиндре без вредного пространства при изменении направления движения поршня. Всасывание изображено процессом 4-1.
Из рис. 5.24 следует, что минимальная работа, затраченная на сжатие газа за один цикл будет при изотермическом процессе (наименьшая площадь цикла 4-1-2-3-4). Однако, изотермическое сжатие газа в поршневых комрессорах нереально. Если в процессе сжатия от газа отводить теплоту, допустим через стенки цилиндра, то работа сжатия будет несколько больше, чем при изотермическом процессе, но меньше, чем при адиабатном. Отсюда в реальных компрессора показатель политропы сжатия находится в пределах 1< n < к.
Значение работы цикла получим интегрирование функции V=f(p) для политропного процесса, т.е.
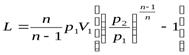 . (5.9)
. (5.9)
Анализ выражения (5.9) показывает, что при неизменных p1 и V1 пот-
ребляемая работа будет тем больше, чем больше значения p2 и n .
5.6.4. Идеальный цикл многоступенчатого компрессора
Как было сказано выше, существует предел степени повышения давления в одной ступени поршневого компрессора. Для получения газа высокого давления применяются многоступенчатые компрессоры, в которых сжатие осуществляется последовательно в нескольких цилиндрах (ступенях) с охлаждением сжимаемого газа после каждой ступени.
Принципиальная схема двухступенчатого компрессора приведена на рис.5.26, а его идеальный цикл в pV – координатах – на рис.5.27.

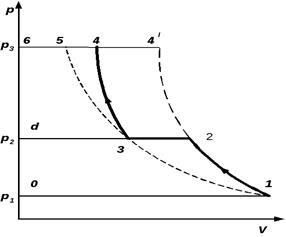
Рис. 5.26 Рис. 5.27
Здесь процессы сжатия газа по ступеням изображены политропами
1-2 и 3-4. Изобара 2-3 характеризует уменьшение объема газа в процессах его охлаждения между ступенями компрессора. Ступенчатое сжатие с промежуточным охлаждением приближает рабочий процесс компрессора к наиболее экономичному изотермическому процессу.
Вся работа, затраченная на привод двухступенчатого компрессора при политропном сжатии газа в каждой ступени, определяется площадью цикла 1-2-3-4-6-0-1. Если процесс сжатия осуществить по политропному процессу в одной ступени до давления p4, то затраченная работа будет больше, чем у двухступенчатого компрессора на величину, эквивалентную площади
2-3-4-4′-2.
Таким образом, многоступенчатое сжатие уменьшает расход энергии на привод компрессора, повышает коэффициент объемной подачи и позволяет получить высокие степени повышения давления.
На примере анализа двухступенчатого компрессора определим, при каком распределении величины  между ступенями работа цикла будет минимальной. Запишем выражение (5.9) для двухступенчатого компрессора:
между ступенями работа цикла будет минимальной. Запишем выражение (5.9) для двухступенчатого компрессора:
 .
.
Обозначим давление p2 = p3 = px и, полагая, что в результате охлаждения газа между ступенями имеет T3 = T1 , получим:
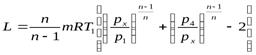
Чтобы определить, при каком рx работа на сжатие будет минимальна, необходимо приравнять к нулю первую производную L по px , т.е.  :
:
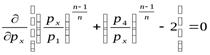 .
.
В результате получим px2 = p1· p4, откуда
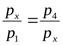 .
.
Следовательно, для двухступенчатого компрессора наименьшая затрата работы будет в случае, когда степень повышения давления в каждой ступени одинакова. Это утверждение для многоступенчатого компрессора записывается выражением:

Так как степень повышения давления в компрессоре 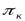 равна произведению
равна произведению 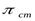 , то
, то
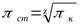 , (5.10)
, (5.10)
где z – число ступеней компрессора.
При заданном значении 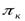 число ступеней определяют по выражению:
число ступеней определяют по выражению:
 (5.11)
(5.11)
С учетом соотношения (5.9) работа для многоступенчатого компрессора при сжатии газа массой m кг может быть вычислена по формуле:
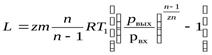 . (5.12)
. (5.12)
Многоступенчатое сжатие
При необходимости достижения высокого давления сжатия компрессоры выполняют многоступенчатыми, причем после каждой ступени рабочее тело поступает в охладитель О, где при постоянном давлении охлаждается до температуры всасывания (рис. 10.7).

Рис. 10.7. Схема двухступенчатого компрессора с промежуточным
Охлаждением рабочего тела
Две причины определяют необходимость многоступенчатого сжатия. Первая из них связана с ограничениями по температуре рабочего тела, т.к. при сжатии до высоких давлений имеет место недопустимое из-за коксования или даже выгорания смазки повышение температуры в конце сжатия выше 200 оС.
Вторая причина выявляется при анализе процессов многоступенчатого (двухступенчатого) сжатия, изображенных на рис. 10.8. Процесс сжатия изображен ломаной линией 12¢1¢2.
| 
|
| а | б |
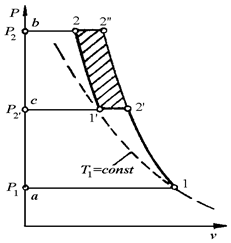
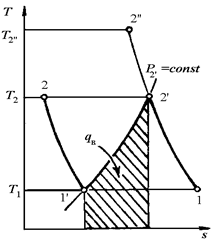
| Рис. 10.8. Процесс сжатия в двухступенчатом поршневом компрессоре: а- в vP – диаграмме; б - в sT – диаграмме. | |
Воздух всасывается в первый цилиндр при давлении 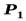 и сжимается в нем по политропе 12¢ до давления
и сжимается в нем по политропе 12¢ до давления 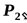 , с которым поступает в холодильник, где по изобаре
, с которым поступает в холодильник, где по изобаре 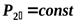 охлаждается до температуры точки 1¢ и уменьшает свой объем. Этот процесс охлаждения изображается отрезком горизонтали 2¢1¢, точка 1¢ лежит так же, как и точка 1 на изотерме 11¢. Из холодильника воздух в состоянии 1¢ всасывается во второй цилиндр и сжимается там по политропе до требуемого давления
охлаждается до температуры точки 1¢ и уменьшает свой объем. Этот процесс охлаждения изображается отрезком горизонтали 2¢1¢, точка 1¢ лежит так же, как и точка 1 на изотерме 11¢. Из холодильника воздух в состоянии 1¢ всасывается во второй цилиндр и сжимается там по политропе до требуемого давления 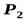 .
.
Вследствие охлаждения рабочего тела в промежуточном охладителе, работа, затрачиваемая на привод многоступенчатого компрессора (пл. а12¢1¢2 b), меньше, чем такая же работа при одноступенчатом сжатии (пл. а12¢¢b) на значение, эквивалентное заштрихованной на vP-диаграмме площади. Вместе с этим выигрыш в работе на привод многоступенчатого компрессора по сравнению с одноступенчатым в какой-то мере декомпенсируется дополнительными затратами энергии на прокачку охлаждающей воды по соответствующим каналам охладителя. Теплота qв, передаваемая охлаждающей воде, в некотором масштабе изображается на sT-диаграмме площадью под кривой процесса охлаждения 2¢1¢ (заштрихованная площадь).
Чем больше число ступеней сжатия и холодильников, промежуточных охладителей, тем ближе будет процесс к изотермическому.
Отношение давлений 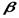 в ступенях задается при проектировании компрессора. В двухступенчатом компрессоре:
в ступенях задается при проектировании компрессора. В двухступенчатом компрессоре: 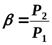 ;
; 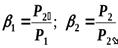 и
и 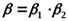
33
Циклы двс
Здравствуйте! Двигатель внутреннего сгорания (ДВС) — это тепловая машина, в которой подвод теплоты к рабочему телу осуществляется за счет сжигания топлива внутри самого двигателя. Рабочим телом в таких двигателях является на первом этапе воздух или смесь воздуха с легковоспламеняемым топливом, а на втором этапе — продукты сгорания.В поршневых двигателях внутреннего сгорания подвод теплоты происходит непосредственно в цилиндре в процессе сгорания топлива. Эти двигатели имеют сравнительно высокую экономичность, малые габариты и вес, приходящийся на единицу мощности, и поэтому в основном применяются в качестве транспортных двигателей: в авиации, автомобильном, водном и железнодорожном транспорте. Кроме того, они используются в стационарных энергетических установках малой мощности.
Недостатком поршневых двигателей является необходимость применения кривошипного механизма, предназначенного для преобразования поступательного движения поршня во вращательное. Наличие несбалансированных масс в кривошипном механизме при увеличении числа оборотов приводит к возникновению больших механических нагрузок. Поэтому мощные двигатели внутреннего сгорания выполняются тихоходными, что увеличивает их габариты и вес.
Различные требования, предъявляемые к двигателям внутреннего сгорания в зависимости от их назначения, привели к созданию самых разнообразных типов этих двигателей. Однако с термодинамической точки зрения их можно классифицировать по характеру процессов. Циклы, которые применяются в двигателях, можно подразделить на следующие три вида:
1) цикл с подводом теплоты при постоянном объеме;
2) цикл с подводом теплоты при постоянном давлении;
3) смешанный цикл, в котором теплота подводится при постоянном объеме и при постоянном давлении.
Смешанный цикл.
Двигатели, работающие по смешанному циклу, являются более совершенными по сравнению с двигателями с изобарным сгоранием, так как у них отсутствует компрессор. Первый патент на бескомпрессорный двигатель высокого давления был выдан в 1901 г. русскому инженеру Г. В. Тринклеру. Однако эти двигатели получили широкое распространение значительно позже, когда удалось осуществить тонкое распыливание топлива с помощью топливного насоса и форсунок специальной конструкции. В настоящее время по смешанному циклу работают преимущественно транспортные двигатели, в которых используется тяжелое топливо.
В смешанном цикле, как и в цикле с изобарным сгоранием, сжатию подвергается воздух. Топливо подается в цилиндр с помощью насоса в конце сжатия (точка 2 на рис. 4) при давлении 30—150 МПа и вследствие высокой температуры воздуха самовоспламеняется. Подача топлива под большим давлением создает благоприятные условия для хорошего распиливания и перемешивания его с воздухом, что обеспечивает достаточно полное сгорание топлива и повышение экономичности двигателя. Процесс горения идет сначала при постоянном объеме (изохора 2—3), а затем при постоянном давлении (изобара 3—3').
Решение
Находим КПД цикла:
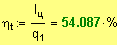
Третье начало термодинамики
Третье начало термодинамики - закон термодинамики, сформулированный В. Нерстом в 1906 году (тепловой закон Нернста), согласно которому энтропия S любой системы стремится к конечному для неё пределу, не зависящему от давления, плотности или фазы, при стремлении температуры (Т) к абсолютному нулю.
Третье начало термодинамики позволяет находить абсолютное значения энтропии, что нельзя сделать на основе первого и второго начал термодинамики. В классической термодинамике (первого и второго начал) энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S0, что практически не мешает большинству термодинамических исследований, так как реально измеряется разность энтропий (S0) в различных состояниях. Согласно третьему началу термодинамики при Т = 0 значение DS = 0.
М. Планк в 1911 году дал другую формулировку третьего начала термодинамики - как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю:
 (8)
(8)
Отсюда S0 = 0. Это даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов.
Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S = klnW.
При абсолютном нуле температуры система находится в основном квантово-механическом состоянии, если оно невырождено, для которого W = 1 (состояние реализуется единственным микрораспределением. Следовательно, энтропия S при Т = 0 равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем может стать существенной при T → 0 дискретность квантовых уровней макроскопической системы, приводящая к явлениям квантового вырождения.
Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достигнуть ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться.
21. Теплопроводность. температурное поле
Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:
- теплопроводностью;
- конвекцией;
- излучением (радиацией).
Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.
Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом.
В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.
Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией). Этот процесс происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение э/м волн в пространстве, поглощение энергии излучения другим телом. Совместный теплообмен излучением и теплопроводностью называют радиационно-кондуктивным теплообменом.
Совокупность всех трех видов теплообмена называется сложным теплообменом.
Процессы теплообмена могут происходит в различных средах: чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т.д. В зависимости от этого теплообмен протекает по разному и описывается различными уравнениями.
Процесс переноса теплоты может сопровождаться переносом вещества (массообмен). Например испарение воды в воздух, движение жидкостей или газов в трубопроводах и.т.п. и.т.д. Тогда процесс теплообмена усложняется, так как теплота дополнительно переносится с массой движущегося вещества.
Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:
t = f(x,y,z,τ) , (9.1)
где:t –температура тела;
x,y,z -координаты точки;
τ - время.
Такое температурное поле называется нестационарным ∂t/∂i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности
Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:
t = f(x,y,z) , ∂t/∂i = 0 (9.2)
Уравнение двухмерного температурного поля:
для нестационарного режима:
t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)
для стационарного режима:
t = f(x,y) , ∂t/∂z = 0; ∂t/∂i = 0 (9.4)
Уравнение одномерного температурного поля:
для нестационарного режима:
t = f(x,τ) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i ¹ 0 (9.5)
для стационарного режима:
t = f(x) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i = 0 (9.6)
Изотермической поверхностью называется поверхность тела с одинаковыми температурой.
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + ∆t.Градиентом температуры называют предел отношения изменения температуры∆tк расстоянию между изотермами по нормали ∆n, когда стремится к нулю:
gradt = |gradt| = lim[∆t/∆n]∆n→0 = ∂t/∂n (9.7)

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормалиn:
gradt = ∂t/∂n no , (9.7*)
где:no –единичный вектор.
Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком – Q, [Вт=Дж/с].
Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – q = Q / F, [Вт/м2]
Для твердого тела уравнение теплопроводности подчиняется закону Фурье:
||Тепловой поток, передаваемая теплопроводностью,||пропорциональна градиенту температуры и площади сечения,||перпендикулярного направлению теплового потока.
Q = -λ∙F∙ ∂t/∂n, (9.8)
или
q = -λ ∙ ∂t/∂n ∙no = -λ∙gradt , (9.9)
где: q –вектор плотности теплового потока;
λ – κоэффициент теплопроводности, [Вт/(м∙К)].
Численное значение вектора плотности теплового потока равна:
q = -λ∙ ∂t/∂n = -λ∙|gradt| , (9.10)
где:|gradt|- модуль вектора градиента температуры.
Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту, Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.
Дифференциальное уравнение теплопроводности для трехмерного нестационарного температурного поля имеет следующий вид:
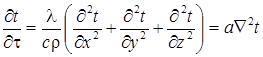 , (9.11)
, (9.11)
где: а = λ/(с·ρ) –коэффициент температуропроводности [м2/с], характеризует скорость изменения температуры.
Для стационарной задачи, дифференциальное уравнение имеет вид:
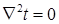 . (9.12)
. (9.12)
22.
Конвективным теплообменом, или теплоотдачей, называется процесс переноса тепла между поверхностью твердого тела и жидкой средой. При этом перенос тепла осуществляется одновременным действием теплопроводности и конвекции.
Явление теплопроводности в жидкостях и газах, так же как и в твердых телах, вполне определяется коэффициентом теплопроводности и температурным градиентом (см. разд. 2). Иначе обстоит дело с явлением конвекции — вторым элементарным видом распространения тепла. Здесь процесс переноса тепла неразрывно связан с переносом самой среды. Поэтому конвекция возможна лишь в жидкостях и газах, частицы которых легко могут перемещаться.
По природе возникновения различают два вида движения — свободное и вынужденное. Свободным называется движение, происходящее вследствие разности плотностей нагретых и холодных частиц жидкости в поле тяжести. Возникновение и интенсивность свободного движения определяются тепловыми условиями процесса и зависят от рода жидкости, разности температур, напряженности гравитационного поля и объема пространства, в котором протекает процесс. Свободное движение называется также естественной конвекцией. Вынужденным называется движение, возникающее под действием посторонних возбудителей, например насоса, вентилятора и пр. В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.
Интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи  , который определяется по формуле Ньютона
, который определяется по формуле Ньютона
|
Q = (tc - tж).
Согласно этому закону количество переданного тепла Q пропорционально поверхности теплообмена F и разности температур стенки и жидкости (tc—tж).
Коэффициент теплоотдачи можно определить как количество тепла, переданное в единицу времени через единицу поверхности при разности температур между поверхностью и жидкостью в один градус:
|

В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и различают поэтому средний по поверхности коэффициент теплоотдачи и локальный или местный коэффициент теплоотдачи, соответствующий единичному элементу поверхности.
Процессы теплоотдачи неразрывно связаны с условиями движения жидкости. Как известно из курса гидравлики, имеются два основных режима течения: ламинарный и турбулентный. При ламинарном режиме течение имеет спокойный, струйчатый характер. При турбулентном — движение неупорядоченное, вихревое. Изменение режима движения происходит при некоторой «критической» скорости, которая в каждом конкретном случае различна.
В результате специальных исследований О. Рейнольдс в 1883 г. установил, что в общем случае режим течения жидкости определяется не только одной скоростью, а особым безразмерным комплексом, состоящим из скорости движения жидкости w, коэффициента кинематической вязкости жидкости v и характерного размера l канала или обтекаемого тела. Теперь такой комплекс называется критерием или числом Рейнольдса и обозначается символом Re = wl/v.
Как известно из гидродинамики, критерий Рейнольдса, называемый иначе критерием кинематического подобия, характеризует соотношение между инерционными силами и силами трения и является основной характеристикой, определяющей режим течения жидкости. Переход ламинарного режима в турбулентный происходит при критическом значении этого критерия Reкр. Например, при движении жидкости в трубах Reкр=wкpd/v=2·103.
При турбулентном движении весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и исчезают. В точности механизм вихреобразования еще не установлен. Одной из причин их возникновения является потеря устойчивости ламинарного течения, сопровождающаяся образованием завихрений, которые затем диффундируют в ядро и, развиваясь, заполняют весь поток. Одновременно с этим вследствие вязкости жидкости эти вихри постепенно затухают и исчезают. Благодаря непрерывному образованию вихрей и их диффузии происходит сильное перемешивание жидкости, называемое турбулентным смешением. Чем больше вихрей, тем интенсивнее перемешивание жидкости и тем больше турбулентность потока. Различают естественную и искусственную турбулентность. Первая устанавливается естественно. Для случая стабилизированного движения внутри гладкой трубы турбулентность вполне определяется значением критерия Re. Вторая вызывается искусственным путем вследствие наличия в потоке каких-либо преград, турбулизирующих решеток и других возмущающих источников. Однако при любом виде турбулентности в тонком слое у поверхности из-за наличия вязкого трения течение жидкости затормаживается и скорость падает до нуля. Этот слой принято называть пограничным или вязким подслоем.
Теория пограничного слоя была разработана Л. Прандтлем в начале прошлого столетия (1904 г.)
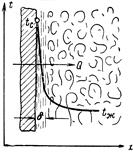
Рис. 4-1. Характер изменения температуры в пограничном слое при нагревании жидкости.
Для процессов теплоотдачи режим движения рабочей жидкости имеет очень большое значение, так как им определяется механизм переноса тепла. При ламинарном режиме перенос тепла в направление нормали к стенке в основном осуществляется путем теплопроводности. При турбулентном режиме такой способ переноса тепла сохраняется лишь в вязком подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемешивания частиц жидкости. В этих условиях для газов и обычных жидкостей интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим. В этом легко убедиться, если проследить за изменением температуры жидкости в направлении нормали к стенке (рис. 4.1). Как видно, наибольшее изменение температуры происходит в пределах тонкого слоя у поверхности, через который тепло передается путем теплопроводности. Следовательно, как для ламинарного, так и для турбулентного режима течения вблизи самой поверхности применим закон Фурье:
|
q = -λ grad t,
где grad t — градиент температуры в слоях жидкости, прилегающих к поверхности твердого тела, °С/м.
Процесс теплоотдачи является сложным процессом, а коэффициент теплоотдачи является сложной функцией различных величин, характеризующих этот процесс. В общем случае коэффициент теплоотдачи является функцией формы Ф, размеров l1, l2, ..., температуры поверхности нагрева tс, скорости жидкости w, ее температуры tж, физических свойств жидкости — коэффициента теплопроводности λ, теплоемкости ср, плотности ρ, вязкости μ и других факторов:
|
α=f(w, tc, tж, λ, ср, ρ, μ, а, Ф, l1 , l2...).
В качестве теплоносителей в настоящее время применяются самые разнообразные вещества — воздух, газы, вода, масла, бензол, нефть, бензин, спирты, расплавленные металлы и различные специальные смеси. В зависимости от рода и физических свойств этих веществ теплоотдача протекает различно и своеобразно. Для каждого теплоносителя физические свойства имеют определенные значения и, как правило, являются функцией температуры, а некоторые из них и давления.
Коэффициент теплопроводности λ характеризует способность вещества проводить тепло; его значение определяет количество тепла, которое проходит в единицу времени через 1 м2 сечения при изменении температуры в один градус на 1 м пути теплового потока (см. разд. 2).
Удельная теплоемкость с определяет количество тепла, необходимое для нагревания 1 кг вещества на один градус. При постоянном давлении теплоемкость обозначается cр (изобарная теплоемкость), а при постоянном объеме cv (изохорная теплоемкость).
Плотность вещества ρ = m/V представляет собой массу вещества в единице объема.
Коэффициент температуропроводности а=λ/сρ характеризует скорость изменения температуры в теле (см. разд. 2).
Вязкость. Все реальные жидкости обладают вязкостью; между частицами или слоями, движущимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. Согласно закону вязкого трения Ньютона эта сила, отнесенная к единице поверхности, пропорциональна изменению скорости в направлении нормали к этой поверхности:
|
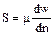 .
.
Величина μ называется коэффициентом вязкости или коэффициентом динамической вязкости.
При dw/dn=1 S = μ, следовательно, коэффициент вязкости выражает собой силу трения, приходящуюся на единицу поверхности соприкосновения двух жидких слоев, «скользящих» друг по другу при условии, что на единицу длины нормали к поверхности скорость движения изменяется на единицу.
В уравнения гидродинамики и теплопередачи часто входит отношение коэффициента вязкости к плотности, называемое коэффициентом кинематической вязкости:
|
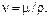
Температурный коэффициент объемного расширения 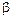 характеризует относительное изменение объема при изменении температуры на один градус:
характеризует относительное изменение объема при изменении температуры на один градус:
|
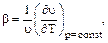
где υ — удельный объем, м3/кг.
Для газов температурный коэффициент объемного расширения определяется по формуле
|
β=1/T.
Механизм и интенсивность переноса теплоты зависят от характера движения жидкости в пограничном слое. Если движение внутри теплового пограничного слоя ламинарное, то теплота в направлении, перпендикулярном к стенке, переносится теплопроводностью. Однако у внешней границы слоя, где температура по нормали к стенке меняется незначительно, преобладает перенос теплоты конвекцией вдоль стенки.
При турбулентном течении в тепловом пограничном слое перенос теплоты в направлении к стенке в основном обусловлен турбулентным перемешиванием жидкости. Интенсивность такого переноса теплоты существенно выше интенсивности переноса теплоты теплопроводностью. Однако непосредственно у стенки, в ламинарном подслое, перенос теплоты к стенке осуществляется обычной теплопроводностью.
Изменение физических свойств жидкости в пограничном слое зависит от температуры, в связи с чем интенсивность теплообмена между жидкостью и стенкой оказывается различной в условиях нагревания и охлаждения жидкости. Так, например, для капельных жидкостей интенсивность теплообмена при нагревании будет большей, чем при охлаждении, вследствие уменьшения пограничного слоя. Следовательно, теплоотдача зависит от направления теплового потока.
Очень большое значение для теплообмена имеют форма и размер поверхностей; в зависимости от них может резко меняться характер движения жидкости и толщина пограничного слоя.
Закон Стефана — Больцмана.
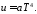
Уравнение является аналитическим выражением закона Стефана - Больцмана, т. е. объемная плотность энергии равновесного излучения пропорцональна абсолютной температуре в четвертой степени.
Обычно в технической литературе закон Стефана — Больцмана пишут в следующем виде:
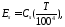
где Сs — коэффициент излучения абсолютно черного тела:
Закон Кирхгофа.
Для всякого тела энергия излучения и энергия поглощения зависят от температуры и длины волны. Различные тела имеют различные значения Е иА. Зависимость между ними устанавливается законом Кирхгофа.
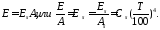
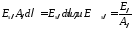 .
.
Из закона Кирхгофа следует, что если тело обладает малой поглощательной способностью, то оно одновременно обладает и малой излучательной способностью (полированные металлы). Абсолютно черное тело, обладающее максимальной поглощательной способностью, имеет и наибольшуюизлучательную способность.
26. интенсификация теплообмена. типы теплообменнх аппаратов\
Одно из направлений интенсификации теплообмена в ТА связано с применением различно профилированных трубок. По мнению специалистов [1-7], реальное применение в конденсирующих ТА могут найти трубки, у которых искусственная шероховатость имеет место как с наружной, так и с внутренней стороны. Интенсификация теплообмена с паровой стороны при этом определяется изменением гидродинамики пленки конденсата на профилированной поверхности трубки - уменьшением за счет действия сил поверхностного натяжения средней толщины пленки конденсата, изменением траектории ее движения и турбулизацией. Интенсификация с водяной стороны также определяется гидродинамикой потока - нарушением упорядоченного течения жидкости в вязком подслое за счет его турбулизации и закрутки. Однако необходимо учитывать, что использование таких трубок приводит к увеличению гидравлического сопротивления ТА, а значит, требует проведения исследований для обоснования целесообразности использования профилированных трубок и выбора оптимальных параметров их профилирования применительно к конкретным ТА и условиям эксплуатации ПТУ. Анализ состояния вопроса [1-7] показал, что для обоснования целесообразности применения различно профилированных трубок в ТА ПТУ необходимо накопление и обобщение данных стендовых исследований и натурных испытаний с целью уточнения методик расчета аппаратов.
Исследование гидродинамики и теплообмена при конденсации пара на различно профилированных трубках проводилось на: профильных витых трубках (ПВТ), продольно-профилированных трубках (ППТ), трубках двойного профиля (ТДП) и встречно-винтовых трубках (ВВТ) [1,2].
Опытами установлено, что гидродинамика пленки конденсата на вертикальной ПВТ существенно отличается от гидродинамики пленки на гладкой трубке. На профильной трубке наблюдается процесс стягивания пленки в канавку и закрутки. При уменьшении шага между канавками S угол отклонения траектории движения пленки от вертикального направления увеличивается и происходит стягивание пленки конденсата в канавки за счет сил поверхностного натяжения.
Относительный эффект интенсификации теплоотдачи при конденсации неподвижного пара на вертикальной ПВТ зависит в основном от режима течения пленки конденсата и параметров профилирования трубок. Интенсивность теплообмена при конденсации пара на поперечно обтекаемой вертикальной ПВТ в зависимости от параметров процесса и параметров профилирования до 2,5 раз выше, чем при конденсации неподвижного пара на гладкой трубке.
Известно, что применение вертикальных ППТ [1,2] позволяет существенно (до 3,5 раз) повысить коэффициент теплоотдачи со стороны конденсирующегося пара. Это объясняется действием на пленку конденсата сил поверхностного натяжения на профилированной криволинейной поверхности трубки. На выступах трубки происходит более интенсивная конденсация пара, т.е. теплообмен фактически лимитируется толщиной пленки конденсата, стекающей по канавкам.
Было предложено дополнительно профилировать ППТ винтовой накаткой, аналогичной ПВТ. При этом предполагалось, что эффект интенсификации будет реализовываться как на наружной поверхности трубки (за счет изменения гидродинамики пленки конденсата), так и внутри нее (за счет турбулизации пристенного слоя теплоносителя). Опытами установлено, что ППТ позволяет повысить уровень теплоотдачи при конденсации водяного пара в среднем в два раза по сравнению с гладкой трубкой. Теплоотдача со стороны конденсирующегося пара на ТДП в зависимости от разности температур "пар-стенка" увеличивается в 1,8-2,2 раза по сравнению с ППТ. В данном случае, по-нашему мнению, проявляются два эффекта: винтовая канавка, заполняясь конденсатом из области продольных канавок, частично отводит его по нисходящей спирали; при этом за счет поворотов часть конденсата с поверхности трубки сбрасывается; винтовая выдавка металла продольных выступов, внедряясь в область течения конденсата в продольных канавках, образует в них чередующиеся локальные сужения, что вносит возмущение в "толстую" ламинарную пленку конденсата, стекающую по продольным канавкам. Первый эффект приводит к уменьшению средней толщины пленки конденсата, а второй - к ее дополнительной турбулизации. Сумма этих эффектов и вызывает интенсификацию теплообмена со стороны конденсирующегося пара.
Одной из перспективных поверхностей для теплообменных аппаратов ПТУ является трубка со встречной винтовой накаткой (ВВТ). Исследования теплообмена при конденсации неподвижного пара показали, что коэффициент теплопередачи ВВТ на 20-30% выше, чем близких по параметрам накатки ПВТ.
Результатами сравнительных испытаний более 100 различных конденсирующих ТА с ПВТ установлено, что интенсификация теплообмена в зависимости от параметров профилирования трубок и режима течения в них воды (при оптимально выбранных параметрах ПВТ) составила от 10 до 80%. Гидравлическое сопротивление ТА при этом возрастает примерно на такую же величину.
Известно [8], что организация режима капельной конденсации пара является самым перспективным направлением интенсификации теплообмена при конденсации пара. Результаты исследований применения нового гидрофобизатора (полифторалкилдисульфид) для трубок из материалов МНЖ5-1 и Л68 показали, что уровень коэффициента теплоотдачи со стороны пара в три- четыре раза превышает теплоотдачу при пленочной конденсации. Опытами установлено, что при попадании в пар воздуха (в момент отключения установки) эффект интенсификации теплообмена резко уменьшается и наблюдается режим смешанной конденсации пара. При возобновлении опыта режим капельной конденсации восстанавливался через 15-20 часов работы установки. После возобновления капельной конденсации уровень теплообмена восстанавливался практически до первоначальной величины. Этот очень важный для практики результат может быть объяснен с учетом современных представлений по динамике биологических систем на основе проведенных спектрометрических исследований гидрофобного покрытия трубок после серии опытов по капельной конденсации. Использованный в опытах стимулятор капельной конденсации имеет в своей структуре как гидрофобный, так и гидрофильный фрагменты. Это увеличивает число степеней свободы конформационного расположения цепи. При резком снижении температуры и отключении подачи в установку пара реализуется более компактная конформация с обнажением гидрофильного фрагмента молекулы. Все это приводит к реализации режима пленочной (смешанной) конденсации в первоначальный момент после повторного включения пара. В дальнейшем водородные связи вызывают самоорганизацию мономолекулярного покрытия с обнажением только гидрофобных участков молекул, что и обеспечивает возобновление режима капельной конденсации. Фактически наблюдается новый тип самоорганизующейся мономолекулярной пленки, которая в зависимости от внешних условий может находиться в различных конформационных состояниях. Коэффициент теплопередачи при капельной конденсации пара на гладкой горизонтальной трубке (МНЖ5-1) в 1,5-2,0 раза выше, чем при пленочной конденсации.
Результаты стендовых испытаний по применению гидрофобизатора на ПВТ (гидрофобизатор наносился на выступы ПВТ) показали, что на вертикальных ПВТ наблюдался отрыв и сброс стекающей пленки конденсата с поверхности трубки в зонах капельной конденсации, что, по-нашему мнению, вызывало уменьшение количества стекающего конденсата по поверхности вертикальной ПВТ и приводило к повышению уровня теплопередачи на 15-25%,
Результаты полупромышленных испытаний опытного модуля (56 горизонтальных трубок, материал - МНЖ5-1), включенного параллельно конденсатору турбины К-300-240 на Рефтинской ГРЭС, проведенных совместно с НПО ЦКТИ, показали, что гидрофобизатор при однократном нанесении на поверхность теплообмена обеспечил поддержание режима капельной конденсации в течение более 4500 часов; при этом коэффициент теплопередачи за счет организации режима капельной конденсации увеличился на 35-70%.
Вибрация трубок теплообменных аппаратов отражается на характере течения пленки конденсата и, следовательно, на теплоотдаче от конденсирующегося пара.
Обобщение экспериментальных данных показало, что в зависимости от удельной паровой нагрузки и параметров вибрации коэффициент теплоотдачи при конденсации пара на вибрирующей горизонтальной трубке может увеличиваться или уменьшаться по сравнению с коэффициентом теплоотдачи при конденсации пара на неподвижной трубке.
Результаты экспериментального исследования обобщены зависимостями, которые дают возможность рассчитать величину поправки к коэффициенту теплоотдачи с паровой стороны для горизонтальных и вертикальных ТА.
Как показывают расчеты, влияние вибрации трубок горизонтальных сетевых подогревателей на теплоотдачу со стороны конденсирующегося пара при характерном для ПСГ уровне удельных паровых нагрузок выражается в увеличении коэффициента теплоотдачи с паровой стороны на величину от 1,6 до 6,7%.
По результатам проведенных стендовых исследований и промышленных испытаний можно предложить ряд практических рекомендаций по повышению эффективности теплообменных аппаратов ПТУ:
- - Выбор наиболее эффективных параметров профилирования трубок необходимо производить на основе оптимизации параметров профилирования и технико-экономического анализа всей ПТУ.
- - При использовании в ТА продольно-профилированных трубок и трубок двойного профилирования можно принять, что теплопередача при конденсации пара увеличивается на 40-150% в зависимости от плотности теплового потока.
- - При использовании в теплообменных аппаратах профилированных трубок с целью повышения надежности соединения трубок с трубными досками концы трубок должны предусматриваться гладкими в пределах 150-200 мм.
- - Применение нового перспективного гидрофобизатора в конденсирующих ТА ПТУ позволяет увеличивать коэффициент теплоотдачи до 3 раз по сравнению с пленочной конденсацией пара. Однако с течением времени идет некоторое понижение коэффициента теплопередачи.
Считаем, что решение вопроса о целесообразности применения любой разработки по повышению эффективности ТА ПТУ должно производиться на основе комплексного технико-экономического анализа для всей энергоустановки. При этом любой ТА необходимо рассматривать не изолированно, а как органичный элемент ПТУ. Основы такой комплексной технико-экономической методики для конкретных ТА ПТУ и конкретных условий эксплуатации на ТЭС представлены в работах [2,9].
Виды теплообменных аппаратов
Теплообменные аппараты классифицируют по:
- по конструкции – аппараты, изготовленные из труб (кожухотрубчатые, «труба в трубе», оросительные, погружные, змеевиковые, воздушного охлаждения); аппараты, поверхность теплообмена которых изготовлена из листового материала (пластинчатые, спиральные, сотовые); аппараты с поверхностью теплообмена, изготовленной из неметаллических материалов (графита, пластмасс, стекла и др.);
- по назначению – холодильники, подогреватели, испарители, конденсаторы;
- по направлению движения теплоносителей – прямоточные, противоточные, перекрестного тока и др.
В общем выпуске теплообменных аппаратов для химической и смежных отраслей промышленности в РФ около 80% занимают кожухотрубчатые теплообменники. Эти теплообменники достаточно просты в изготовлении и надежны в эксплуатации и в то же время достаточно универсальны.
Теплообменники типа «труба в трубе» и змеевиковые стальные в общем объеме теплообменной аппаратуры составляют около 8%, а оросительные из чугуна – около 2%.
2. Кожухотрубчатые теплообменники
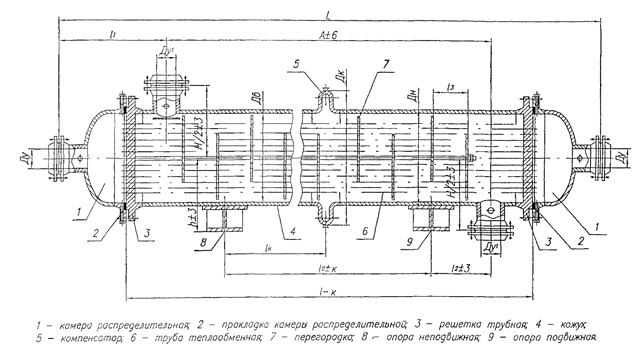
Рис.1. Кожухотрубчатый теплообменник
Кожухотрубчатые теплообменники относятся к наиболее распространенным. Их применяют в промышленности и на транспорте в качестве нагревателей, конденсаторов, охладителей, для различных жидких и газообразных сред. Основными элементами кожухотрубчатого теплообменника являются: кожух (корпус), трубный пучок, камеры-крышки, патрубки, запорная и регулирующая арматура, контрольная аппаратура, опоры, каркас. Кожух аппарата сваривают в виде цилиндра из одного или нескольких, обычно стальных листов. Толщина стенки кожуха определяется максимальным давлением рабочей среды в межтрубном пространстве и диаметром аппарата. Днища камер могут быть сферическими сварными, эллиптическими штампованными и реже – плоскими. Толщина днищ не должна быть меньше толщины корпуса.
Предпочтительнее вертикальное расположение корпуса и всего теплообменника, так как в этом случае уменьшается площадь, занимаемая аппаратом, и более удобно расположение его в рабочем помещении.

Рис. 2. Трубные пучки кожухотрубчатых теплообменников
Трубный пучок теплообменника может быть собран из гладких стальных бесшовных, латунных или медных прямых или U- и W-образных труб диаметром от нескольких миллиметров до 57 мм и длиной от нескольких сантиметров до 6–9 м с диаметром корпуса до 1,4 м и более. Внедряются, особенно в холодильной технике и на транспорте, образцы кожухотрубчатых и секционных теплообменников с низкими накатными продольными, радиальными и спиральными ребрами. Высота продольного ребра не превышает 12–25 мм, а высота выступа катаных труб 1,5–3,0 мм при 600–800 ребрах на 1 м длины. Внешний диаметр труб с низкорадиальными (накатными) ребрами мало отличается от диаметра гладких труб, хотя поверхность теплообмена при этом возрастает в 1,5–2,5 раза. Форма такой поверхности теплообмена обеспечивает высокую тепловую эффективность аппарата при рабочих средах с различными теплофизическими свойствами.
В зависимости от конструкции пучка как гладкие, так и накатные трубы закрепляют в одной или двухтрубных решетках развальцовкой, разбортовкой, сваркой, спайкой или сальниковыми соединениями. Из всех перечисленных способов реже применяют более сложные и дорогостоящие сальниковые уплотнения, допускающие при тепловых удлинениях продольное перемещение труб.
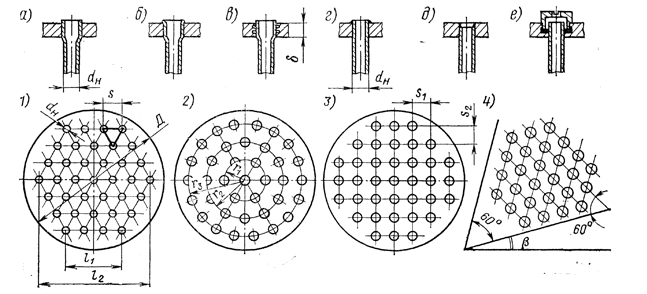
Рис. 3. Способы закрепления и размещения труб в трубных решетках: а – развальцовкой; б – развальцовкой с отбортовкой; в – развальцовкой в очках с канавками; г и д – приваркой; е – с помощью сальника; 1 – по сторонам и вершинам правильных шестиугольников (треугольников); 2 – по концентрическим окружностям; 3 – по сторонам и вершинам квадратов; 4 – по сторонам и вершинам шестиугольников со смещенной на угол β диагональю.
Размещение труб в трубных решетках (рис. 3.) может быть осуществлено несколькими способами: по сторонам и вершинам правильных шестиугольников (шахматное), по сторонам и вершинам квадратов (коридорное), по концентрическим окружностям и по сторонам и вершинам шестиугольников со смещенной на угол β диагональю. Преимущественно трубы размещаются равномерно на всей площади решетки по сторонам и вершинам правильных шестиугольников. В аппаратах, предназначенных для работы на загрязненных жидкостях, часто принимают прямоугольное размещение труб для облегчения очистки межтрубного пространства.
В горизонтальных кожухотрубчатых теплообменниках–конденсаторах с целью уменьшения термического сопротивления на внешней поверхности труб, вызываемого пленкой конденсата, трубы рекомендуется размещать по сторонам и вершинам шестиугольника со смещенной на угол β диагональю, оставляя при этом в межтрубном пространстве свободные проходы для пара.
Некоторые варианты компоновки трубных пучков в корпусе приведены на (рис. 4.). Если обе решетки пучка из прямых труб зажимаются между верхними и нижними фланцами корпуса и крышек, то такой аппарат будет жесткой конструкции (рис.4. а, б). Теплообменники жесткой конструкции применяются при сравнительно небольшой разности температур между корпусом и трубами (примерно 25–30° С) и при условии изготовления корпуса и труб из материалов с близкими значениями их коэффициентов удлинения. При проектировании аппарата необходимо рассчитывать напряжения, возникающие вследствие тепловых удлинений труб в трубной решетке, особенно в местах соединения труб с решеткой. По этим напряжениям в каждом конкретном случае определяют пригодность или непригодность аппарата жесткой конструкции. Возможные варианты кожухотрубчатых теплообменников нежесткой конструкции показаны также на (рис. 4., в, г, д, е).
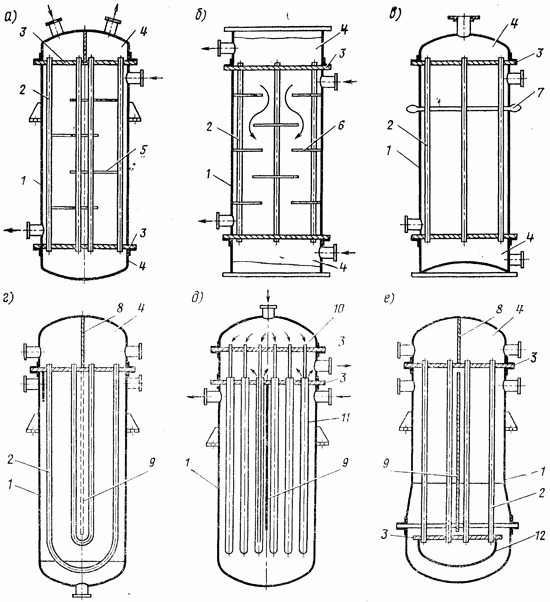
Рис. 4. Схемы кожухотрубчатых теплообменников: а – с жестким креплением трубных решеток с сегментными перегородками; б – с жестким креплением трубных решеток с кольцевыми перегородками; в – с линзовым компенсатором на корпусе; г – с U-образными трубами; д – с двойными трубами (труба в трубе); е – с «плавающей» камерой закрытого типа; 1 – цилиндрический корпус; 2 – трубы; 3 – трубная решетка; 4 – верхняя и нижняя камеры; 5, 6, 9 – сегментная, кольцевая и продольная перегородки в межтрубном пространстве; 7 – линзовый компенсатор; 8 – перегородка в камере; 10 – внутренняя труба; 11 – наружная труба; 12 – «плавающая» камера.
В теплообменниках с U-образными (рис.4., г), а также с W-образными трубами оба конца труб закрепляют в одной (чаще в верхней) трубной решетке. Каждая из труб пучка может свободно удлиняться независимо от удлинения других труб и элементов аппарата. При этом в местах соединений труб с трубной решеткой и в соединении трубной решетки с корпусом не возникает никаких напряжений. Эти теплообменники пригодны для работы при высоких давлениях теплоносителей. Однако аппараты с гнутыми трубами не могут быть признаны лучшими из-за трудности изготовления труб с разным радиусом изгиба, сложности замены и неудобства очистки гнутых труб.
В кожухотрубчатых теплообменниках с двойными трубами (рис.4., д) каждый элемент состоит из двух труб: наружной – с закрытым нижним концом и внутренней – с открытым концом. Верхний конец внутренней трубы меньшего диаметра закрепляют развальцовкой или сваркой в верхней трубной решетке, а трубу большего диаметра – в нижней трубной решетке. При таких условиях монтажа каждый из элементов, состоящий из двух труб, может свободно удлиняться без возникновения тепловых напряжений. Нагреваемая среда движется по внутренней трубе, затем по кольцевому каналу между наружной и внутренней трубами. Тепловой поток от греющей к нагреваемой среде передается сквозь стенку внешней трубы. Кроме того, в процессе переноса теплоты участвует и поверхность внутренней трубы, потому что температура нагреваемой среды в кольцевом канале выше температуры той же среды во внутренней трубе.
27. основные положения и законы теории массообмена. основные соотношения и модели
| Основные положения и законы теории массообмена ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ТЕОРИИ МАССОПЕРЕНОСА 1. Общие сведения В природе и технике наряду с теплообменными широко распространены и массообменные процессы. Очень часто они идут совместно, и от интенсивности одних зависит скорость других. В природе это, например, - процессы переноса теплоты и массы воздушными и водяными течениями и процессы окисления веществ в живых организмах. В технике — процессы восстановления металлов из руд и окисления (горения) топлив, примесей и железа при плавке и нагреве стали. В теории массообмена различают массоотдачу и массопередачу. Массоотдача — перенос массы в пределах одной фазы (гомогенный массоперенос), а массопередача — перенос одного или нескольких веществ из одной фазы в другую через поверхность раздела фаз (гетерогенный массоперенос). Состав фаз выражают: в объемных концентрациях, кг/мэ или кмоль/м3 ; в массовых или мольных долях, кг/100 кг или кмоль/ЮО кмоль. Состав газовых смесей выражают парциальными давлениями. Основную часть жидкой или газообразной фазы, в которой поле концентраций компонентов постоянно, называют ядром. Дело в том, что на поверхности раздела фаз концентрации компонентов отличаются от концентраций этих же веществ в ядрах. Изменение концентраций от значений на границе до их величины в ядре происходит в пределах тонкого пограничного слоя между поверхностью раздела фаз и ядром. Несмотря на относительное перемещение фаз, режим движения в концентрационном пограничном слое очень часто сохраняется ламинарным. Перенос массы между фазами происходит до наступления подвижного равновесия, при котором из одной фазы во вторую переносится столько же вещества, сколько его переходит на второй фазы в первую. Массообмен в пределах одной фазы заканчивается после выравнивания концентраций по всему объему. Массообмен — самопроизвольный процесс переноса какого-либо вещества в форме молекул, атомов, ионов в пространстве с неоднородной концентрацией этого вещества. Массообмен имеет место и при неоднородных полях температур и давлений в рассматриваемом объеме. Молекулярную диффузию под действием неоднородного распределения концентраций в объеме называют концентрационной диффузией. Если причиной диффузии являются разности'(градиенты) температур или давлений, то эти виды диффузионного переноса вещества называют термо- или бародиффузией. Вещество может переноситься под одновременным воздействием нескольких градиентов: концентраций, температур и давлений. Перенос массы помимо молекулярной диффузии может также осуществляться движущимися массами (конвекцией). Совместный перенос массы молекулярной диффузией и конвективным переносом называют конвективным массообменом. Молекулярная диффузия имеет место в неподвижных потоках или в пограничных слоях, находящихся вблизи границы раздела фаз. Она обусловливается беспорядочным движением частичек переносимого вещества. Перенос вещества под действием турбулентных пульсаций называют турбулентной диффузией. Направление переноса вещества внутри фазы или между фазами определяется градиентом его концентраций в отдельных точках системы. Вещество всегда переходит из фазы, где его содержание выше равновесного, в фазу или область, в которых его концентрация ниже равновесного значения (или от большего градиента к меньшему). Скорость массопередачи связана с механизмом переноса распределяемого вещества между фазами, между которыми происходит массообмен. Наиболее распространенные процессы массопередачи в металлургии: абсорбция — поглощение газа жидкостью; адсорбция — поглощение газов, паров или жидкостей твердыми поглотителями; восстановление — удаление кислорода из оксидов металлов (руд); десорбция — процесс обратной абсорбции и адсорбции; насыщение — обогащение поверхностных слоев стали одним или несколькими химическими элементами; окисление — соединение горючего вещества с окислителем, например, при горении топлива в рабочем пространстве печей или горение некоторых химических элементов в расплавах (стали, штейне и т. д.); растворение твердых веществ в жидкостях; сушка - удаление влаги из твердых материалов путем ее испарения. Многие технологические процессы в металлургии реализуются несколькими одновременно протекающими гетерогенными процессами массопереноса. Причем направление переноса веществ из фазы в фазу определяется его концентрациями в фазах и условиями равновесия. Перенос массы в процессах сопровождается переносом энергии. Плотность потока массы, кг/(м2 • К), вещества т, переносимого молекулярной диффузией в бинарных (двухкомпонентных) смесях, можно определить по первому закону Фика: m^-D^dc/dri), (5. 1) где Dj — коэффициент диффузии i-того компонента, м2 /с; dc/dn — градиент концентраций, кг/м4 . Смысл коэффициента диффузии, кг • м/[(кг/мэ ) • с], можно понять из формулы D = mdn/dc. Следовательно, он определяет количество вещества, диффундирующего в единицу времени через единицу поверхности при градиенте концентраций, равном 1. Это физическая константа, не зависящая от гидродинамических условий массопереноса. Бе значение зависит от вида переносимого вещества, свойств среды, через которую оно диффундирует, температуры и давления. Коэффициенты диффузии газа в среду другого газа составляют 0,1 — 1 см2 /с, а диффузии газа в жидкости ~ 1 см2 /(сут), т. е. в 1 - 105 меньше. Следовательно молекулярная диффузия — весьма медленный процесс. Обычно величина коэффициента диффузии в газах в литературе приводится для Г0 = 273 К и р0 = 1 • 105 Па. Поэтому ее обозначают DQ . Значения D при иных давлениях можно вычислить по формуле D = D0 (p/P0 )3 '2 . В справочниках коэффициенты диффузии в жидкостях даны для температуры 20 °С (р20 ). Пересчитать эту величину для другой температуры можно по формуле D = D3 O [l + d(r-20)], где d = 6,33 i0 '5 /p°>33 . В последнем выражении ц — динамический коэффициент вязкости растворителя, Па • с; р — плотность растворителя, кг/м3 . Для газовых фаз закон Фика можно выразить с помощью уравнения состояния идеальных газов. Концентрация какого-либо компонента фазы, кг/м3 , с = 1/у = р/(ЯГ). Здесь v — удельный объем компонента при его локальном парциальном давлении р, м3 /кг; R — газовая постоянная, Дж/(кг ■ К); Т — температура компонента, К; р — местное парциальное давление диффундирующего компонента, Па. При Г- const — = (RT)-4p/un и m—[D/(«T)]dp/dn = -D dp/dn. dn Здесь Dp — коэффициент молекулярной диффузии газа в газе, отнесенный к градиенту парциального давления, с. Для бинарной смеси (состоящей из двух компонентов) коэффициенты диффузии компонентов и Dp неодинаковы вследствие различия газовых постоянных. Поэтому их отношение, при D г = D2 где Ц1 и Ц2 — молекулярные массы компонентов бинарной смеси, кг/моль. Знак минус с правой части закона Фика указывает на то, что поток массы и градиент концентрации направлены в противоположные стороны. Для бинарной смеси справедливо соотношение D1 = D2 , т. е. коэффициенты диффузии взаимно диффундирующих веществ равны. Для многокомпонентной смеси это соотношение не выполняется. Плотность потока массы, переносимой в пределах фазы турбулентной диффузией, m = -DT (dc/dn), (5. 2) где Dx — коэффициент турбулентной диффузии, зависящий только от гидродинамических условий процесса (с* орости потока, масштаба турбулентности), м2 /с. Известно, 4ToDI >D. В жидкостях и газах суммарный перенос массы молекулярной и конвективной диффузией определяется выражением m ■ mM + mK = — Ddc/dn + cw, (5. 3) где mR — плотность потока массы, переносимой конвективной диффузией, С — концентрация диффундирующего вещества внутри фазы, кг/м3 ; w — скорость потока вещества внутри фазы, м/с. В (5. 3) градиент концентрации и скорость потока противоположны по направлению. Движение потока значительно увеличивает перенос массы, поэтому тк ~> тм . Плотность потока массы, кг/(м2 • с), внутри фазы, например, от поверхности раздела в ядро, можно вычислить по уравнению т = В(сп -с0 ). (5. 4) Здесь (сп — cQ ) — разность концентраций, являющаяся движущей силой процесса; с. — средняя концентрация в ядре потока; сп — средняя концентрация на поверхности раздела фаз; В — коэффициент массоотдачи. Он определяет количество массы, переносимой от поверхности раздела фаз в ядро фазы (или в обратном направлении) через единицу поверхности в единицу времени при движущей силе (сп — cQ ) равной единице. Он не является физическим свойством вещества; это — кинетическая характеристика, зависящая не только от свойств фазы, но и от гидродинамических условий течения потока. Этот коэффициент учитывает как молекулярный, так и турбулентный перенос вещества. Коэффициент массоотдачи может быть выражен в разных единицах в зависимости от выбранной системы выражения движущей силы процесса переноса вещества. В общей форме В = m/Дс = кг [м2 • с (е. д. с.)], где е. д. с. — единицы движущей силы. Если движущей силой процесса переноса является разность объемных концентраций, кг/м3 , то коэффициент массоотдачи, м/с, обозначают р0 . Если же разность концентраций выражена в относительных единицах (кг/кг или кмоль/кмоль), то коэффициент массоотдачи, кгДм2 • с), обозначают Рс или рт соответственно. Если же движущей силой переноса является разность парциальных давлений, Па, то коэффициент массоотдачи, с/м, обозначают Рр . Уравнение (5. 4) — аналог уравнения Ньютона - Рихмана. Интенсифицировать массообменные процессы можно за счет повышения коэффициента массоотдачи или увеличения площади поверхности, воспринимающей или отдающей массу, так как разность концентраций устанавливается условиями технологического процесса. Чаще всего прибегают к увеличению поверхности массообмена /, осуществляя, например, обработку материала в слое. Если температура диффундирующего газа не изменяется по объему фазы, то и уравнения состояния газа можно записать, что концентрации сп -1/тп -Рп /(ЙТ) и с0 = 1/у0 = р0 /(ЙГ). Поэтому разность концентраций сп - cQ = (рп - р0 )/(КГ). Здесь vn и v0 - удельны! объемы диффундирующего газа при их парциальных давлениях рп и р0 , м3 /кг; рп и Р0 - парциальные давления газа у поверхности фаз и в ядре, Па. При подстановке последнего соотношения в (5. 4) получим формулу Дальтона для т, кг/(м2 • с): т-[р/(йГ)](рп -р0 ) = рр (рп -р0 ), (5. 3) где рр — коэффициент массоотдачи, отнесенный к разности парциальных давлений. Коэффициенты массоотдачи можно определить следующим образом. Примем, что у поверхности раздела фаз существует ламинарный концентрационный пограничный слой, перенос массы в котором происходит молекулярной диффузией в соответствии с первым законом Фика: m - -Ddc/dn = р(с„ - с0 ) = р Ас. Поэтому P = -(D/Ac)dc/dn. Если вместо разности концентраций воспользоваться разностью парциальных давл то рр = -(£>р/Др) dp/dn = -[Dp /(pn - p0 )]dp/dn, где Dp = D/(RT) — коэффициент молекулярной диффузии какого-либо компон фазы, отнесенный к градиенту парциального давления, с. Из вышеизложенного хорошо просматривается аналогия между Р и коэффици конвективной теплоотдачи, поэтому для отыскания величины коэффициентов ма отдачи применимы все те методы конвективного теплопереноса, которые были расе рены ранее. |
Теплообменные устройства
Теплообменный аппарат (теплообменник) — это устройство, в котором осуществляется теплообмен между двумя или несколькими средами. Устройства, в которых между средами происходит массообмен, называют массообменными аппаратами. Аппараты, в которых одновременно протекают тепло- и массообмен, называют тепломассообменными. Движущиеся среды, обменивающиеся теплотой или применяемые для передачи теплоты от более нагретых тел и веществ к менее нагретым, называют теплоносителями.
Наибольшее распространение в тепломассообменных и теплотехнологических установках получили следующие процессы: нагревание, охлаждение, конденсация, выпаривание, сушка, дистилляция, плавление, кристаллизация, затвердевание. По потенциалу теплоносителя теплотехническое оборудование можно разделить на низкотемпературное, среднетемпературное и высокотемпературное. К высокотемпературным установкам относятся промышленные печи, им соответствуют рабочие температуры в пределах 400...2000 °С. Низко- и среднетемпературное оборудование представляет собой теплообменные аппараты, установки для тепловлажностной обработки и сушки материалов и изделий, установки утилизации тепла и пр. Рабочий диапазон среднетемпературных процессов и установок находится, как правило, в пределах 150...700 °С. Процессы с более низкими температурами, до -150 °С, называют криогенными.
Изучение тепло- и массообменных процессов и установок дает возможность правильно осуществлять выбор теплоиспользующего оборудования для решения вопросов по экономии энергоресурсов на промышленных объектах, а это является одной из задач в работе инженера-энергетика.
По типу взаимодействия сред
Поверхностные
Теплообменные аппараты данного вида подразумевают, что среды (теплоноситель и теплопотребитель) между собой не смешиваются, а теплопередача происходит через контактную поверхность – пластины в пластинчатых теплообменниках или трубки в кожухотрубных.
Смесительные
Кроме поверхностных теплообменников используются агрегаты, в основе эксплуатации которых лежит непосредственный контакт двух веществ.
Наиболее известным вариантом смесительных теплообменников являются градирни:

Рис. 2. Градирни – один из видов смесительных ТО
Градирни используются в промышленности для охлаждения больших объемов жидкости (воды) направленным потоком воздуха.
К смесительным теплообменникам относятся:
- паровые барботеры;
- сопловые подогреватели;
- градирни;
- барометрические конденсаторы.
По типу передачи тепла
Рекуперативные
В данном виде устройств теплопередача происходит непрерывно через контактную поверхность. Примером такого теплообменного аппарата является пластинчатый разборный теплообменник.
Регенеративные
Отличаются от рекуператоров тем, что движение теплоносителя и теплопотребителя имеют периодический характер. Основная область применения таких установок – охлаждение и нагрев воздушных масс.
Установки с подобным типом действия нужны в многоэтажных офисных зданиях, когда теплый отработанный воздух выходит из здания, но его энергию передают свежему входящему потоку.
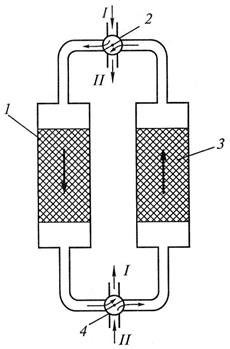
Рис. 3. Регенеративный теплообменник
На изображении видно, как в теплообменник поступают 2 потока: горячий (I) и холодный (II). Проходя через коллектор 1,горячая среда нагревает гофрированную ленту, свернутую в спираль. В это время через коллектор 3, проходит холодный поток.
Спустя какое-то время (от нескольких минут до нескольких часов), когда коллектор 1, заберет достаточное количество тепла (точное время зависит от тех. процесса), крыльчатки 2 и 4 поворачиваются.
Таким образом изменяется направление потоков I и II. Теперь холодный поток идет через коллектор 1 и забирает тепло.
По типу конструкции
Вариаций конструкций теплообменных аппаратов очень много. Их выбор и подбор конкретной модели зависит от большого количества условий эксплуатации и технических характеристик:
- мощность теплообменника;
- давление в системе;
- тип сред (агрессивные или нет);
- рабочие температуры;
- прочие требования.
Подробную классификацию типов конструктивов теплообменных аппаратов можно посмотреть выше на Рис. 1.
Рис. 10.7. Схема двухступенчатого компрессора с промежуточным
Охлаждением рабочего тела
Две причины определяют необходимость многоступенчатого сжатия. Первая из них связана с ограничениями по температуре рабочего тела, т.к. при сжатии до высоких давлений имеет место недопустимое из-за коксования или даже выгорания смазки повышение температуры в конце сжатия выше 200 оС.
Вторая причина выявляется при анализе процессов многоступенчатого (двухступенчатого) сжатия, изображенных на рис. 10.8. Процесс сжатия изображен ломаной линией 12¢1¢2.
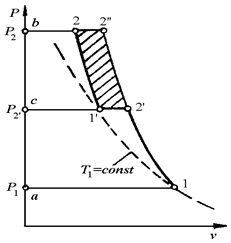
| 
|
| а | б |
| Рис. 10.8. Процесс сжатия в двухступенчатом поршневом компрессоре: а- в vP – диаграмме; б - в sT – диаграмме. | |
Воздух всасывается в первый цилиндр при давлении  и сжимается в нем по политропе 12¢ до давления
и сжимается в нем по политропе 12¢ до давления  , с которым поступает в холодильник, где по изобаре
, с которым поступает в холодильник, где по изобаре  охлаждается до температуры точки 1¢ и уменьшает свой объем. Этот процесс охлаждения изображается отрезком горизонтали 2¢1¢, точка 1¢ лежит так же, как и точка 1 на изотерме 11¢. Из холодильника воздух в состоянии 1¢ всасывается во второй цилиндр и сжимается там по политропе до требуемого давления
охлаждается до температуры точки 1¢ и уменьшает свой объем. Этот процесс охлаждения изображается отрезком горизонтали 2¢1¢, точка 1¢ лежит так же, как и точка 1 на изотерме 11¢. Из холодильника воздух в состоянии 1¢ всасывается во второй цилиндр и сжимается там по политропе до требуемого давления  .
.
Вследствие охлаждения рабочего тела в промежуточном охладителе, работа, затрачиваемая на привод многоступенчатого компрессора (пл. а12¢1¢2 b), меньше, чем такая же работа при одноступенчатом сжатии (пл.а12¢¢b) на значение, эквивалентное заштрихованной на vP-диаграмме площади. Вместе с этим выигрыш в работе на привод многоступенчатого компрессора по сравнению с одноступенчатым в какой-то мере декомпенсируется дополнительными затратами энергии на прокачку охлаждающей воды по соответствующим каналам охладителя. Теплота qв, передаваемая охлаждающей воде, в некотором масштабе изображается на sT-диаграмме площадью под кривой процесса охлаждения 2¢1¢ (заштрихованная площадь).
Чем больше число ступеней сжатия и холодильников, промежуточных охладителей, тем ближе будет процесс к изотермическому.
Отношение давлений  в ступенях задается при проектировании компрессора. В двухступенчатом компрессоре:
в ступенях задается при проектировании компрессора. В двухступенчатом компрессоре:  ;
;  и
и 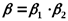 .
.
Циклы паросиловой установки
В паросиловых установках в качестве рабочего тела используются пары различных жидкостей (вода, ртуть и т. п.), но чаще всего водяной пар.
В паровом котле паросиловой установки (1) за счет подвода теплоты Q1, получаемой за счет сгорания топлива в топке, образуется пар при постоянном давлении р1 (рис. 33). В пароперегревателе (2) он дополнительно нагревается и переходит в состояние перегретого пара. Из пароперегревателя пар поступает в паровой двигатель (3) (например, в паровую турбину), где полностью или частично расширяется до давления р1 с получением полезной работы L1. Отработанный пар направляется в холодильник-конденсатор (4), где он полностью или частично конденсируется при постоянном давлении р2. Конденсация пара происходит в результате теплообмена между отработавшим паром и охлаждающей жидкостью, протекающей через холодильник-конденсатор (4).
|
После холодильника сконденсированный пар поступает на вход насоса (5), в котором давление жидкости повышается с величины р2 до первоначального значения р1 после чего жидкость поступает в паровой котел (1). Цикл установки замыкается. Если в холодильнике (4) происходит частичная конденсация отработавшего пара, то в паросиловой установке вместо насоса (5) используется компрессор, где давление пароводяной смеси также повышается с р2 до р1. Однако для того, чтобы уменьшить работу на сжатие, целесообразно полностью сконденсировать пар в конденсаторе и затем сжимать не пароводяную смесь, а выходящую из конденсатора воду. Описанный цикл паросиловой установки называется циклом Ренкина (рис. 34).
Цикл Ренкина состоит из изобары (4–1), где подводится теплота в нагревателе, адиабаты (1–2) расширения пара в паровой турбине, изобары (2–3) отвода теплоты в холодильнике-конденсаторе и изохоры (3–4) повышения давления воды в насосе. Линия (4–а) на изобаре соответствует процессу повышения температуры жидкости после насоса до температуры кипения  при давлении р1. Участок (a–b) соответствует превращению кипящей жидкости в сухой насыщенный пар, а участок (b–1) – процессу подвода теплоты в пароперегревателе для превращения сухого насыщенного пара в перегретый.
при давлении р1. Участок (a–b) соответствует превращению кипящей жидкости в сухой насыщенный пар, а участок (b–1) – процессу подвода теплоты в пароперегревателе для превращения сухого насыщенного пара в перегретый.
а б
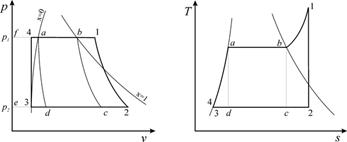
Рис. 34. Цикл Ренкина в координатах p-v (а) и Т-s (б)
Работа, совершаемая паром в турбине, равна разности энтальпий пара до и после турбины
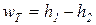 . (306)
. (306)
Работа, затраченная на сжатие воды в насосе, определяется так же по разности энтальпии рабочего тела в точках (4) и (3).
В координатах р-v эта работа определяется площадью e-3-4-f (рис. 34a). Эта работа весьма мала по сравнению с работой турбины.
Полезная работа цикла равна работе турбины за вычетом работы, затрачиваемой на привод насоса wН
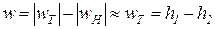 . (307)
. (307)
Удельное количество теплоты q1, подведенной в котле и пароперегревателе, определяется из первого начала термодинамики (работа при этом не совершается) как разность энтальпий рабочего тела в процессе подвода теплоты
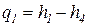 , (308)
, (308)
где h4 – энтальпия горячей воды на входе в паровой котел при давлении р2 практически равна по величине энтальпии кипящей воды в точке (3),
т.е. h4 @ h3.
Сопоставляя соотношения, можно определить термический КПД цикла Ренкина как отношение полезно полученной работы в цикле к количеству подведенной теплоты
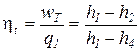 . (309)
. (309)
Другая важная характеристика паросиловой установки – удельный расход пара d, который характеризует количество пара, необходимого для выработки 1 кВт·ч энергии (3600 Дж), и измеряется в  .
.
Удельный расход пара в цикле Ренкина равен
 . (310)
. (310)
Удельный расход пара определяет размеры агрегатов: чем он больше, тем больше пара приходится вырабатывать для получения той же мощности.
Пути повышения экономичности паросиловых установок
Термический КПД цикла Ренкина даже в установках с высокими параметрами пара не превышает 50 %. В реальных установках из-за наличия внутренних потерь в двигателе значение КПД еще меньше.
Существуют два пути повышения экономичности паросиловых установок: повышение параметров пара перед турбиной и усложнение схем паросиловых установок.

| ||||
| ||||
1 – парогенератор; 2 – пароперегреватель; 3 – паровая турбина;
4 – конденсатор; 5 – питательный насос; 6 – тепловой потребитель
Первое направление приводит к увеличению теплоперепада в процессе расширения пара на турбине (h1 - h2) и, как следствие, к увеличению удельной работы и КПД цикла. При этом теплоперепад по турбине h1-h2 можно дополнительно увеличить, снижая противодавление в конденсаторе установки, т.е. уменьшая давление р2.Повышение экономичности паросиловых установок этим путем связано с решением ряда трудных технических задач, в частности, использования высоколегированных, жаропрочных материалов для изготовления турбины.
Эффективность использования паросиловой установки можно значительно повысить за счет использования теплоты отработавшего пара для отопления, горячего водоснабжения, сушки материалов и т. д. С этой целью охлаждающую воду, нагретую в конденсаторе (4) (рис. 35), не выбрасывают в водоем, а прокачивают через отопительные установки теплового потребителя (6). В таких установках станция вырабатывает механическую энергию в виде полезной работы L1 на валу турбины (3) и теплоту Qт.п для отопления. Такие станции называют теплоэлектроцентралями (ТЭЦ). Комбинированная выработка тепловой и электрической энергии – один из основных методов повышения эффективности тепловых установок.
Повысить КПД паросиловой установки по сравнению с циклом Ренкина можно за счет применения так называемого регенеративного цикла
(рис. 36). В этой схеме питательная вода, поступающая в котел (1), нагревается паром, частично отбираемым из турбины (3). По этой схеме пар, полученный в котле (1) и перегретый в пароперегревателе (2), направляется в турбину (3), где происходит его расширение до давления в конденсаторе (4). Однако часть пара после совершения им работы из турбины и направляется в регенеративный подогреватель (6), где в результате конденсации он подогревает питательную воду, подаваемую насосом (5) в котел (1).
Сам конденсат после регенеративного подогревателя поступает на вход насоса (5) или в конденсатор 4, где он смешивается с конденсатом пара, прошедшего через все ступени турбины. Таким образом, в котел поступает такое же количество питательной воды, какое и выходит из него в виде пара. Из диаграмм (рис. 37) видно, что каждый килограмм пара, входящий в турбину, расширяется от давления р1 до давления р2, совершая работу w1=h1-h2. Пар в количестве (1 - g) долей килограмма расширяется до конечного давления p3, совершая работу w2=h2-h3. Суммарная работа 1 кг пара в регенеративном цикле будет
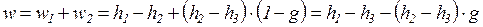 , (311)
, (311)
где  – доля пара отбираемого из турбины и подаваемого в регенератор.
– доля пара отбираемого из турбины и подаваемого в регенератор.
Рис. 37. График адиабатного расширения пара в турбине с промежуточным отбором (а) и изменения количества пара (б)
Уравнение показывает, что использование регенерации теплоты приводит к уменьшению удельной работы расширения по сравнению с циклом Ренкина с теми же параметрами пара. Однако расчеты показывают, что работа в регенеративном цикле уменьшается медленнее, чем расход теплоты на получение пара при наличии регенерации, поэтому КПД паросиловой установки с регенеративным подогревом в итоге выше КПД обычного цикла.
Применение пара высоких и сверхвысоких давлений с целью повышения КПД установок наталкивается на серьезное затруднение: влажность его на последних ступенях турбины получается настолько высокой, что заметно снижает КПД турбины, вызывает эрозию лопаток, может служить причиной выхода их из строя. Поэтому в установках с высокими параметрами пара приходится применять так называемый промежуточный перегрев пара, что также ведет к повышению КПД установки (рис. 38).
Рис. 38. Схема паросиловой установки с промежуточным перегревом пара:
1 – парогенератор; 2 – пароперегреватель; 3 – турбина высокого давления (ТВД); 4 – турбина низкого давления (ТНД); 5 – конденсатор; 6 – питательный насос; 7 – промежуточный пароперегреватель; 8 – потребитель
В паросиловой установке с промежуточным перегревом пара, после расширения в турбине высокого давления (3) пар отводится в специальный пароперегреватель (7), где он вторично подогревается при давлении ррп до температуры 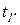 , которая обычно несколько ниже, чем температура t1. Перегретый пар поступает в турбину низкого давления (4), расширяется в ней до конечного давления р2 и уходит в конденсатор (5) (рис. 39).
, которая обычно несколько ниже, чем температура t1. Перегретый пар поступает в турбину низкого давления (4), расширяется в ней до конечного давления р2 и уходит в конденсатор (5) (рис. 39).
Влажность пара после турбины при наличии перегрева пара значительно меньше, чем она была бы без него (x1>x2) (рис. 39). Применение промежуточного перегрева в реальных условиях дает повышение КПД приблизительно на 4 %. Этот выигрыш получается не только за счет повышения относительного КПД турбины низкого давления, но и за счет повышения суммарной работы расширения пара по турбине низкого и высокого давлений. Дело в том, что сумма отрезков  и
и  , характеризующих работу соответственно турбин высокого и низкого давлений, больше отрезка 1 – e, характеризующего работу расширения в турбине установки, в которой не применяется промежуточного перегрева пара (рис. 39б).
, характеризующих работу соответственно турбин высокого и низкого давлений, больше отрезка 1 – e, характеризующего работу расширения в турбине установки, в которой не применяется промежуточного перегрева пара (рис. 39б).
а б
Рис. 39. Процесс расширения пара в установке с промежуточным перегревом
Холодильные машины
Холодильная машина – устройство для отвода теплоты от охлаждаемого тела, температура которого должна быть ниже, чем температура окружающей среды. Холодильные машины используются для получения температур от 10 до -1500 С.Область более низких температур относится к криогенной технике. Холодильные машины отнимают теплоту от охлаждаемого тела и передают охлаждающей среде (воде или окружающему воздуху) с затратой энергии.
Применяются несколько типов холодильных машин:
- воздушные холодильные машины;
- паровые компрессорные холодильные машины;
- абсорбционные холодильные машины.
Воздушная холодильная машина. Хладагентом в ней служит воздух. Принцип ее действия заключается в следующем. Воздух из охлаждаемой камеры 3 засасывается компрессором 1, где подвергается адиабатическому сжатию. Сжатый воздух поступает затем в теплообменник 2, где охлаждается водой. Далее воздух направляется в расширительную машину – детандер 4, где расширяется и производит полезную работу. Температура воздуха при расширении снижается до -60…-700 С. Охлажденный воздух затем поступает в холодильную камеру 3, где отнимает тепло от охлаждаемого тела.
Холодильный коэффициент теоретического цикла воздушной холодильной машины равен
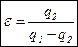 , (3.7)
, (3.7)
где q1 - количество теплоты, отнимаемого от охлаждаемого тела,  ;
;
q2 - количество теплоты, передаваемое охлаждающей воде,  .
.
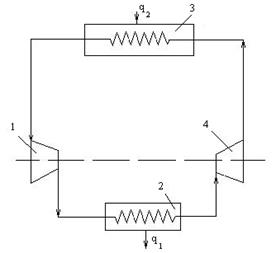
Рис.3.4-Схема воздушной холодильной машины
Паровая компрессорная холодильная машина. Рабочим телом такой машины являются низкокипящие тела: аммиак, фреоны и др. При атмосферном давлении температура их кипения ниже 00 С. Компрессор 1 сжимает пары рабочего тела, которые затем поступают в конденсатор 2, где отдают теплоту при постоянном давлении. Пары при этом конденсируются, превращаясь в жидкость за счет охлаждения водой. Далее жидкость проходит через дроссельный клапан 4, где расширяясь, превращается в пар. Затем рабочее тело виде пара поступает в охлаждаемую камеру 3 (испаритель), где при постоянных давлении и температуре насыщенный пар превращается в нагретый, отнимая теплоту от охлаждаемого тела. Далее пар подается в компрессор и цикл повторяется.
Холодильный коэффициент машины равен
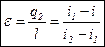 . (3.8)
. (3.8)
где q2 – количество теплоты, отнимаемое от охлаждающего тела,  ;
;
l – затраченная работа,  ;
;
i1 и i2 – энтальпия рабочего тела на входе и выходе из компрессора,  ;
;
i - энтальпия рабочего тела на входе в испаритель, 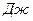 .
.
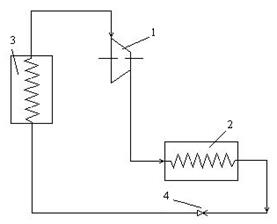
Рис.3.5-Схема паровой компрессорной холодильной машины
Паровая компрессорная холодильная машина имеет более высокий КПД, чем воздушная.
Абсорбционная холодильная машина. В основу принципа действия абсорбционной холодильной машины положено свойство растворов изменять температуру кипения в зависимости от концентрации. В этих машинах в качестве рабочего тела используется водно-аммиачный раствор, температура которого снижается с повышением концентрации аммиака в растворе (рис.3.12.).
Абсорбционная холодильная машина работает следующим образом. Пары аммиака из генератора 1 сжижаются в конденсаторе 2 и через редукционный вентиль 3 поступают в испаритель 4, находящийся в охлаждаемой камере. При дросселировании давление паров падает от рк до давления в испарителе рх, а температура снижается от t1 до t4 . Рабочее тело при этом переходит в газожидкостное состояние, отнимая теплоту Qx.
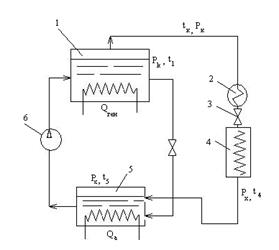
1 – генератор; 2 – конденсатор; 3 – редукционный вентиль;
4 – испаритель; 5 – абсорбер; 6 – насос.
Рис.3.6-Схема абсорбционной холодильной машины
Образовавшиеся в испарителе пары аммиака направляются в абсорбер 5, где поглощаются слабым водно-аммиачным раствором. Здесь использовано свойство слабого аммиачного раствора поглощать холодные пары аммиака. В абсорбер 5 из генератора 1 поступает слабый раствор аммиака, который по мере поглощения паров NH3 понижает свою концентрацию, а также давление паров рх и температуру t5. Насыщенный раствор аммиака насосом 6 перекачивается в генератор 1. В генераторе 1, благодаря подводу извне теплоты Qген, происходит кипение раствора при давлении рк с выделением почти чистого аммиака NH3. По мере отгонки аммиака раствор обедняется и отводится через редукционный вентиль в абсорбер 5. Выделенные пары аммиака поступают в конденсатор 2, где сжижаются путем отвода теплоты Qk. Перекачивающий насос 6 повышает давление раствора от Рх до Рк.Теплота растворения аммиака в абсорбере Qa отводится охлаждающей водой или воздухом.
Эффективность работы абсорбционной холодильной установки оценивается коэффициентом использования тепла
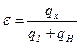 , (3.9)
, (3.9)
где qx – холодопроизводительность, т. е. тепло, отбираемое в испарителе;
q1 – количество тепла, подведенное греющим паром в генераторе;
qH – затраты тепла на работу насоса.
Абсорбционная холодильная машина имеет ряд преимуществ, благодаря которым они получили широкое распространение: простота обслуживания, невысокая стоимость, возможность использования отработанного тепла. К недостаткам относятся низкий КПД, большой расход воды.
Термодинамика и основы статистики.
Основные понятия.
Моделью материального тела является совокупность атомов и молекул, свойства; законы взаимодействия, движения которых известны. Существует два раздела физики: термодинамика и статическая физика- они изучают закономерности процессов в макротелах, состоящих из атомов и молекул. Они изучают тепловые свойства макротел.
Метод термодинамики -- феноменологический(учитывает превращение энергии без учёта природы исследуемых явлений, связанных с молекулярно-кинетической структурой вещества). Метод статической физики -- исследование системы, состоящей из атомов и молекул путём задания уравнений, описывающих поведение совокупности частиц, и с помощью вероятностного метода определяется поведение макросистемы.
Классическая термодинамика, основоположником которой является Томсон, Клаузиус, изучает равновесные системы и процессы в таких системах.
Неравновесная термодинамика. Она ещё развивается и изучает неравновесные системы.
Основоположниками молекулярно - кинетической теории являются Клаузис, Больцман, Максвелл.
Создателем статической физики является Гиббс. В основе статической физики был положен метод Гиббса для равновесных системы.
Дата: 2019-03-05, просмотров: 404.