Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1ГПЗ- задача на построение точек пересечения линий и поверхностей.

2ГПЗ- задача на построение линий пересечения поверхностей.

Решение обеих ГПЗ зависит от расположения ГО ( линий поверхности)

Относительно ПП.

Различают 3 случая:

- оба ГО проецирующие

Решать ничего не надо, проекции искомых геометрических элементов известны, их необходимо выделить и обозначить.

- один ГО проецирующий, второй общего положения.

В этом случае одна проекция искомого геометрического элемента известна, она принадлежит основной проекции проецирующего ГО. Вторую проекцию необходимо строить из условия принадлежности не проецирующего ГО.

- оба ГО общего положения

Алгоритм решения:

а)заключить прямую в проецирующую плоскость

б) построить линию пересечения это плоскости заданной (2ГПЗ2)

в) определить точки пересечения заданной прямой с построенной линией пересечения

г) определить видимость заданной прямой относительно заданной плоскости

 

39. Как определить видимость при пересечении прямой линии с плоскостью?

Взаимное положение прямой линии и плоскости в пространстве может быть следующим: а) прямая лежит в плоскости, б) прямая пересекает плоскость, в) прямая параллельна плоскости. Если на чертеже непосредственно нельзя установить взаимного положения прямой и плоскости, то прибегают к некоторым вспомогательным построениям, в результате которых от вопроса о взаимном положении прямой и плоскости переходят к вопросу о взаимном положении данной прямой и некоторой вспомогательной прямой. 1) через данную прямую проводят вспомогательную плоскость и строят линию пересечения этой плоскости и данной плоскости; 2) устанавливают взаимное положение данной прямой и прямой пересечения плоскостей; найденное положение определяет взаимное положение данных прямой и плоскости. Точки и линии, лежащие для зрителя за плоскостью невидимы, видимыми будут точки и линии, расположенные по одну сторону плоскости со зрителем. Видимые отрезки линий вычерчиваются сплошными линиями, а невидимые – штриховыми.

40. Какая точка из числа расположенных на общем перпендикуляре к горизонтальной плоскости проекций считается видимой на этой плоскости проекций?

Точки на одном проецирующем луче называются конкурирующими. Они в направлении проецирующего луча имеют общую для них проекцию, т.е. их проекции тождественно совпадают. Характерным признаком конкурирующих точек на эпюре является тождественное совпадение их одноименных проекций. Конкуренция заключается в видимости этих проекций относительно наблюдателя. Говоря другими словами, в пространстве для наблюдателя одна из точек видима, другая – нет. И, соответственно, на чертеже: одна из проекций конкурирующих точек видима, а проекция другой точки – невидима.

На пространственной модели проецирования (рис. 5) из двух конкурирующих точек А и В видима точка А по двум взаимно дополняющим признакам. Судя по цепочке S₁→А→В точка А ближе к наблюдателю, чем точка В. И, соответственно, – дальше от плоскости проекций π₁ (т.е. z_A > z_A).

 

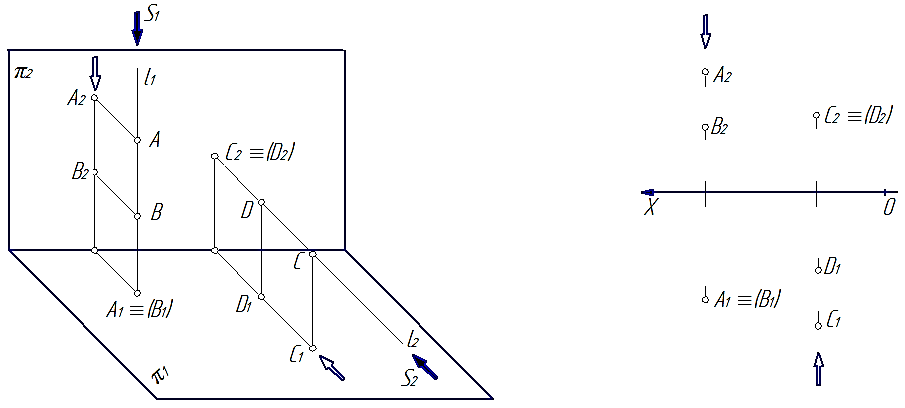
Рис. 5 Рис.6

Если видима сама точка A, то видима и её проекция A₁. По отношению к совпадающей с ней проекцией B₁. Для наглядности и при необходимости на эпюре невидимые проекции точек принято заключать в скобки.

Уберем на модели точки А и В. Останутся их совпадающие проекции на плоскости π₁ и раздельные проекции – на π₂. Условно оставим и фронтальную проекцию наблюдателя (⇩), находящегося в центре проецирования S₁. Тогда по цепочке изображений ⇩ → A₂ → B₂ можно будет судить о том, что z_A > z_B и что видима и сама точка А и её проекция А₁.

Аналогично рассмотрим конкурирующие точки С и D по видимости относительно плоскости π₂. Поскольку общий проецирующий луч этих точек l₂ параллелен оси 0Y, то признак видимости конкурирующих точек С и D определяется неравенством y_C > y_D. Следовательно, что точка D закрыта точкой С и соответственно проекция точки D₂ будет закрыта проекцией точки С₂ на плоскости π₂.

Рассмотрим, как определяется видимость конкурирующих точек на комплексном чертеже (рис. 6).

Судя по совпадающим проекциям А₁≡В₁ сами точки А и В находятся на одном проецирующем луче, параллельном оси 0Z. Значит сравнению подлежат координаты z_A и z_B этих точек. Для этого используем фронтальную плоскость проекций с раздельными изображениями точек. В данном случае z_A > z_B. Из этого следует, что видима проекция А₁.

Точки C и D на рассматриваемом комплексном чертеже (рис. 6) так же находятся на одном проецирующем луче, но только параллельном оси 0Y. Поэтому из сравнения y_C > y_D делаем вывод, что видима проекция С₂.

Общее правило. Видимость для совпадающих проекций конкурирующих точек определяется сравнением координат этих точек в направлении общего проецирующего луча. Видима та проекция точки, у которой эта координата больше. При этом сравнение координат ведется на плоскости проекций с раздельными изображениями точек.

 

41. Что называется многогранником, призмой, пирамидой?

Многогранники

^{Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником (рисунок 35).}

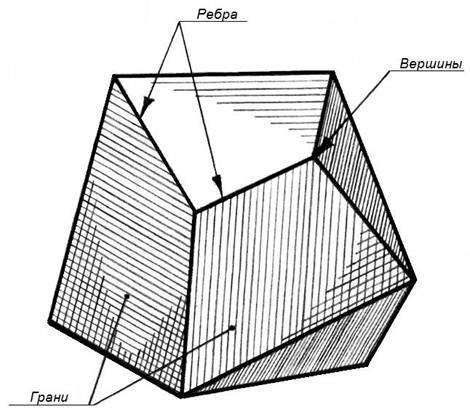
^{Рисунок 35 – Многогранник}

^{Многогранники различают в зависимости от формы и количества граней.}

^{Рассмотрим некоторые из многогранников, которые наиболее часто встречаются в технических чертежах.}

^Призма

^{Призма – многогранник, у которого две грани (основания) n-угольники, расположенные в параллельных плоскостях, а остальныеnграней (боковые грани) – параллелограммы. Призма может быть прямой, если боковые ребра перпендикулярны основанию (рисунок 36) и наклонной, если ребра не перпендикулярны основанию. Прямая призма называется правильной, если в основании у нее правильный многогранник.}

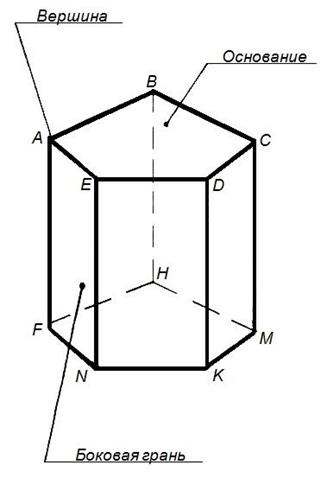
^{Рисунок 36 - Призма}

Пирамида

^{Пирамида – многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину. В основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной (рисунок 37) и т.д.}

^{При изображениях на комплексных чертежах многогранников принято считать, что их грани непрозрачные и поэтому проекции отдельных ребер и граней будут невидимы. При решении вопросов видимости принимается следующие правила (рисунок 38):}

^{1. Линии, образующие внешний контур (очерк) каждой проекции, всегда видимы.}

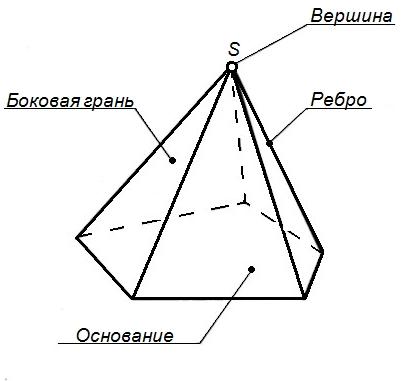
^{Рисунок 37 - Пирамида}

^{2. Если внутри очерка пересекаются проекции двух ребер, то одна из них видимая, а другая невидимая (рисунок 38). Видимость определяется с помощью конкурирующих точек.}

^{3. Если проекция хотя бы одного из ребер, ограничивающих грань, невидимая, то и вся грань невидимая.}

^{4. На видимой грани лежат видимые элементы, на невидимой – невидимые.}

^{5. Если в одной точке сходятся три или более ребер, то они все видимы или все невидимы.}

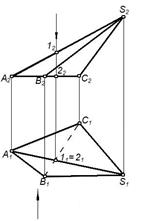
^{Рисунок 38 – Определение видимости пирамиды}

 

42. Чем задается призматическая поверхность?

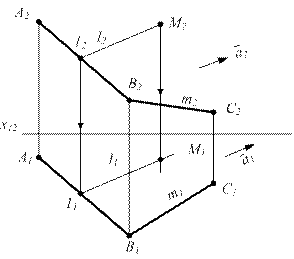
Призматическая поверхность- линейчатая поверхность, образованная параллельным перемещением прямой в пространстве (образующей) и пересекающей ломаную линию (направляющую).

Призматическая поверхность в пространстве и на чертеже задается своим определителем Ф (m; 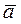)[А]

где m - направляющая;

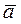- направление перемещения образующей;

М Ì Ф - произвольная точка, принадлежащая поверхности призмы;

l || 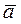- образующая, проходящая через т.М;

l É М и l ∩ m = 1 М2 задана произвольно М2 Î l2 l2 || ā2 l2 ∩ m2 = 12 12 ® 11 и 11Î l1 l1 || ā1 М1 Î l1

Рисунок 3.2

Т.к. М произвольная точка и вторая проекция ее построена, то теорема доказана.

Призма - геометрическая фигура, ограниченная замкнутой призматической повер­хностью и двумя плоскостями.

l ^ П1 Г || П1 П1

Рисунок 3.3

 

43. Какие признаки позволяют установить, что на данном чертеже изображена призма?

Наличие на чертеже только прямолинейных отрезков, причем они служат проекциями или ребер, или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.

Положим, что нам известна по форме и положению фигура, полученная при пересечении всех боковых граней призмы плоскостью, и известно направление ребер призмы (рис. 258). Этим задается призматическая поверхность. Пересекая призматическую поверхность двумя параллельными между собой плоскостями, мы получаем основания призмы (рис. 258). Можно задаться одним из оснований призмы и ее высотой или длиной бокового ребра и тем задать призму.

Выбирая положение призмы для ее изображения, целесообразно располагать ее основания параллельно плоскости проекций.

Какие признаки позволяют установить, что на данном чертеже изображена именно призма (или, в частности, параллелепипед)? Наличие на чертеже только прямолинейных отрезков ²), причем они служат проекциями или ребер, или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.

¹) Мы могли бы считать, что контуру тела в данном случае принадлежат и все точки отрезков АВ,ВС,DB₁, B₁D₁, EF и E₁F₁ и даже площади треугольников АВС и DB₁D₁ и части трапеций EFF₁E₁, так как проецирующие плоскости α₁; α₂ и α₃ проходят соответственно через эти фигуры.

Примеры даны на рис. 258 — 260: здесь в системе π₁, π₂ изображены прямая треугольная призма, наклонная четырехугольная призма и куб (о том, что это именно куб, свидетельствует равенство ребер и прямоугольность граней).

Но для тела, изображенного на рис. 261, несмотря на наличие некоторых из указанных выше признаков, было бы ошибочным утверждать, что это обязательно призма или параллелепипед. На рис. 261 справа показаны возможные варианты решений. Очевидно, в данном случае для уточнения следовало бы иметь профильную проекцию или обозначение вершин.

На рис. 262 изображена неправильная четырехугольная призма (основаниями служат трапеции). На рис. 263 (сверху) показано построение профильной проекции этой призмы с применением вспомогательной прямой. Там же (внизу) показано отнесение призмы к плоскостям координат, совпадающим с ее гранями. В этом случае третья проекция построена по координатам вершин.

 

44. Чем задается поверхность пирамиды?

Для задания поверхности пирамиды надо иметь фигуру сечение всех боковых граней пирамиды плоскостью и точку их пересечения. Обычно пирамида задается на чертеже проекциями ее основания и вершины, а усеченная пирамида – функциями обоих оснований. Выбирая положение пирамиды для ее изображения, целесообразно располагать основание параллельно плоскости проекций

 

45. При каком условии для изображения пирамиды достаточно двух проекций?

 

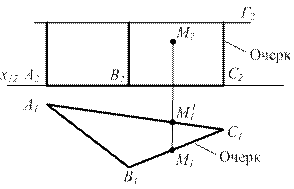
Для построения фигуры, получаемой при пересечении призмы и пирамиды плоскостью, надо или найти точки, в которых ребра призмы или пирамиды пересекают данную плоскость, или найти отрезки прямых, по которым грани призмы или пирамиды пересекаются плоскостью. В первом случае построение сводится к задаче на пересечение прямой с плоскостью, во втором случае — на пересечение плоскостей между собой.

В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид фигуры сечения ¹), то следует применять один из способов, которые позволяют находить длину отрезка, величину угла и т. д. (см. главу V).

На рис. 273 показано пересечение прямой четырехугольной призмы плоскостью, заданной пересекающимися прямыми EF и EG. Обозначим эту плоскость буквой δ.

При пересечении получается четырехугольник, вершины которого представляют собой точки пересечения ребер призмы с пл.δ.Так как в данном случае призма прямая и основание ее параллельно пл. π₁, то горизонтальная проекция фигуры сечения определяется сразу, без какого-либо построения: она накладывается на проекцию A'B'C'D'. Очевидно, можно найти точки К и L, в которых ребра призмы, проходящие через точки А и D, пересекают пл. δ, при помощи одной пл. α, в которой находится грань призмы α × δ = 1—2, откуда получаем точки К" и L".Проведя" пл. β, получим β × δ = 3 — 4 и точки М' и N'.

¹) Выражение «натуральный вид сечения» мы будем применять в том случае, когда фигура сечения дается без искажения.

Итак, способ построения, который указан на рис. 273, сводится к применению вспомогательных плоскостей α и β, проходящих через соответствующие грани призмы, и построению отрезков KL и MN, по которым эти грани пересекаются пл. δ.

На фронтальной проекции линия пересечения состоит из видимой и невидимой частей; видимая часть линии пересечения расположена на обращенных к зрителю видимых гранях.

На рис. 273 находящаяся под пл. δ нижняя часть призмы представлена как невидимая. Линия пересечения лишь прочерчена на гранях призмы.

Если секущая плоскость перпендикулярна к одной из плоскостей проекций (рис. 274, слева), то проекции фигуры сечения получаются без каких-либо дополнительных проекция K"P"M"N" располагается на следе β", горизонтальная проекция K'P'N'M' совпадает с проекцией призмы.

На рис. 274 справа показано пересечение призмы пл. α, заданной пересекающимися прямыми АВ и ВМ₂, из которых ВМ₂ параллельна ребрам призмы. Следовательно, секущая плоскость в данном случае общего положения, параллельная

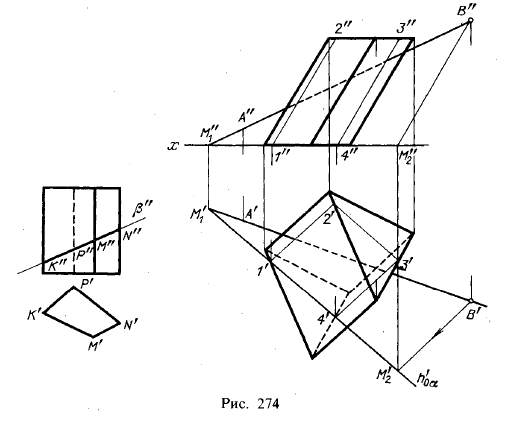
ребрам призмы. Она пересекает призмы по параллелограмму 1 — 2 — 3 — 4, стороны 1 — 2 и 3 — 4 которого параллельны ребрам призмы. Чтобы провести эти стороны, надо построить след пл. α на плоскости основания призмы и пересечь им это основание по прямой 1—4.

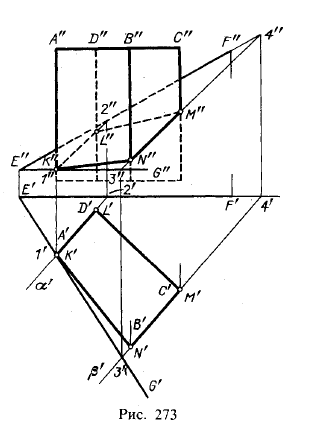
На рис. 275 показано пересечение пирамиды плоскостью общего положения α, выраженной следами. Дело сводится к нахождению точек пересечения ребер SA, SB и SC с пл. α, т. е. к задаче на пересечение прямой с плоскостью (см. § 25). Рассмотрим нахождение точки L, в которой ребро SB пересекает пл. α. Выполняем следующие действия: 1) через SB проводим вспомогательную плоскость, в данном случае горизонтально-проецирующую β; 2) находим прямую пересечения 1—2 плоскостей α и β; 3) находим точку L в пересечении прямых SB и 1 — 2.

Далее, так как в данном случае ребро SA расположено параллельно пл. π₂, проводим через него вспомогательную фронтальную плоскость δ. Она пересекает пл. α

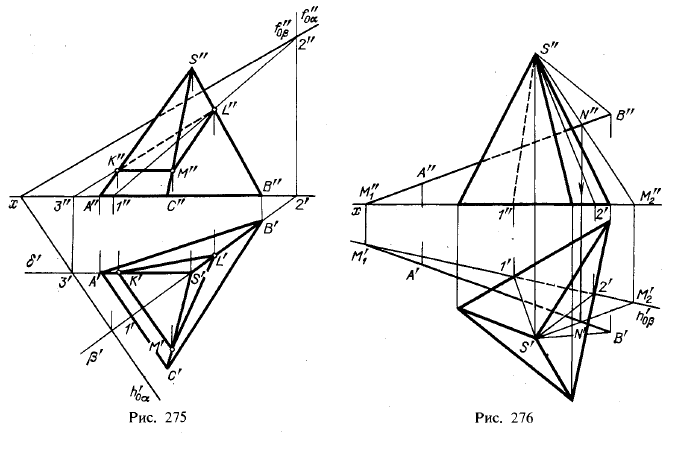
по ее фронтали с начальной точкой 3; в пересечении этой фронтали с ребром SA получаем точку К.

Теперь обратим внимание на другую особенность в данном примере: проекция А'С' параллельна следу h'_0α. Это тот случай, когда у двух плоскостей горизонтальные следы взаимно параллельны (h'_0α|| А'С', но А'С' — часть горизонтального следа плоскости грани SAC) и линия пересечения таких плоскостей является их общей горизонталью. Поэтому мы можем провести через уже найденную точку К прямую, параллельную ребру АС (или ||h'_0α, и так найти точку М.

Если бы не было этих особенностей, то следовало бы поступать аналогично построению точки L.

Чертеж на рис. 275 выполнен согласно условию, что пл. α прозрачна и что основным является нанесение на гранях линий разделения пирамиды на две части.

Пусть (рис. 276) пирамида рассечена пл. α, заданной пересекающимися прямыми АВ и SB, причем SB проходит через вершину пирамиды. Следовательно, пл. α рассекает ее по треугольнику, одна из вершин которого находится в точке S. Чтобы найти две другие вершины треугольника — точки 1 и 2, надо построить след пл. α на плоскости основания пирамиды. Остальное ясно из чертежа.

При пересечении поверхности призмы или пирамиды прямой линией получаются две точки. Для них встречается название точки входа и выхода. Чтобы найти эти точки, надо провести через данную прямую вспомогательную плоскость и найти линии ее пересечения с гранями; эти линии на гранях оказываются расположенными в одной плоскости с данной прямой и в своем пересечении дают точки, в которых данная прямая пересекает поверхность.

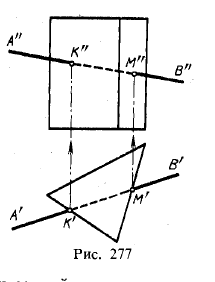
Могут быть случаи, когда нет надобности в таких построениях. Пример дан на рис. 277; положение проекций К' и М' очевидно, так как боковые грани призмы перпендикулярны к пл. π₁. По точкам К' и М' найдены точки К" и М".

На рис. 278 показано построение точек пересечения прямой линии с поверхностью пирамиды. Через прямую АВ проведена вспомогательная фронтально-проецирующая пл. α. Фронтальная проекция фигуры сечения пирамиды этой плоскостью сливается с фронтальной проекцией плоскости; горизонтальная проекция сечения найдена построением. Точки пересечения горизонтальной проекции прямой АВ с горизонтальной проекцией фигуры сечения представляют собой горизонтальные проекции искомых точек; по найденным горизонтальным проекциям (точки К' и М') построены фронтальные проекции (К" и М") точек пересечения.

----------

Построение точек пересечения прямой линии с поверхностью призмы можно представить себе еще следующим образом. Положим, что мы вместо прямоугольного проецирования применим косоугольное. Спроецируем призму и прямую АВ (рис. 279) на пл. π₁ по направлению, параллельному ребрам данной призмы. Призма спроецируется в треугольник C₁D₁E₁, совпадающий е горизонтальной

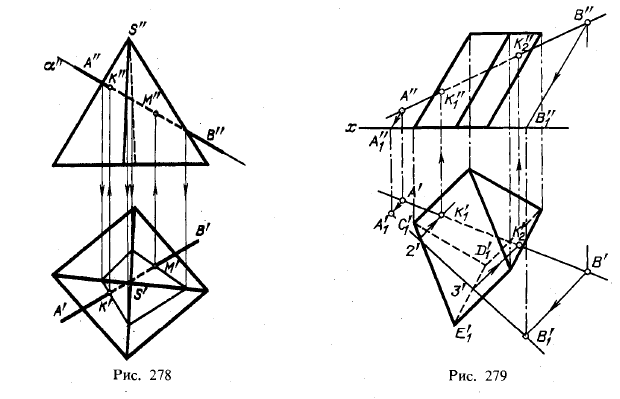
проекцией нижнего основания призмы, а прямая АВ — в прямую А₁В₁, которая пересечет стороны треугольника C₁D₁E₁ в точках 2 и 3. Обратным проецированием мы получим проекции К'₁ и К'₂, а по ним К"₁ и К"₂.

 

46. В какой последовательности строят проекции правильной шестигранной призмы, основания которых расположены на профильной плоскости проекций?

Построение проекций правильной прямой призмы (рисунок 127) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Так как основание призмы параллельно горизонтальной плоскости проекций H, то эта проекция изображается отрезком прямой параллельно оси OX. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых (т.к. они перпендикулярны горизонтальной плоскости проекций). Передняя боковая грань 1243 изображается на фронтальной плоскости проекций V без искажения, а на плоскости H — в виде прямой линии. Фронтальные и профильные проекции остальных граней изображаются с искажением.

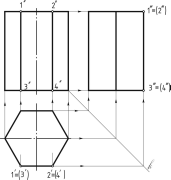
Рисунок 127

На чертеже оси х, у и z не показывают, что делает чертеж более простым.

 

47. Чем отличается призма от пирамиды?

Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена. Пирами́да (др. -греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину [1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.

Рассмотрим прямую призму, которая стоит на горизонтальной плоскости (рис. 56).

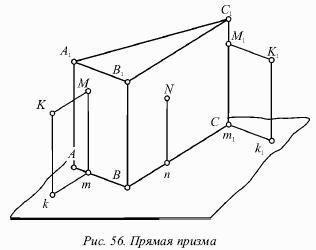
Ее боковые грани являются частями горизонтально-проецирующих плоскостей, а ребра являются отрезками вертикальных прямых. Исходя из этого ребра следует проецировать на горизонтальную плоскость в виде точек, а на фронтальную плоскость – без искажения (АА = а́а́₁ и т. д.).

Нижнее основание призмы АВС находится в горизонтальной плоскости, поэтому ее можно изобразить на этой плоскости без искажения: ΔАВС = Δаbс. Фронтальная проекция пирамиды а́b́с́ совпадает с осью х.

Оба основания дают одинаковые горизонтальные проекции (Δаbс = Δа₁b₁с₁). Верхнее основание А₁В₁С₁ параллельно горизонтальной плоскости, т. е. его фронтальная проекция а́₁b́₁с́₁ параллельна оси х.

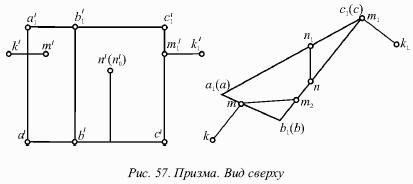
При рассмотрении призмы сверху (рис. 57) будет видно только верхнее основание призмы.

Горизонтальные проекции трех точек, которые лежат на нижнем основании, помещены в скобки с целью показа, того, что точки А, В и С невидимы, если смотреть на призму из данного положения.

Для определения невидимых элементов на фронтальной проекции обращаются к горизонтальной проекции.

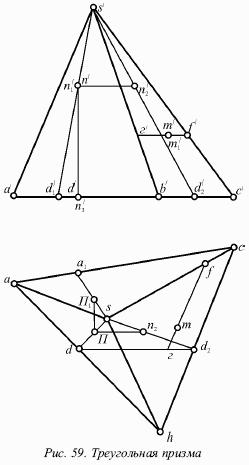
Направление луча зрения показано на рисунке 58 стрелкой. Видно, что грань АА₁С₁С при таком угле зрения будет невидимой.

На рисунке 58 показана треугольная пирамида, которая находится на горизонтальной плоскости.

Гранями пирамиды являются треугольники, являющиеся частями плоскостей общего положения.

Если рассматривать пирамиду сверху, можно увидеть всю ее боковую поверхность, т. е. для горизонтальной проекции не существует невидимых элементов.

Из рассуждений, подобных рассуждениям в случае призмы, можно убедиться, что на фронтальной проекции невидима грань SАС (рис. 59).