Рис. 2.5
екции используются при выполнении перспективных рисунков предметов, сооружений и др. (рис. 2.6).
Если центр проецирования удалить в бесконечность, то все проецирующие лучи будут параллельны друг другу. Такой метод проецирования называется параллельным, а полученная проекция — параллельной. В природе примером параллельного проецирования являются солнечные или лунные тени.
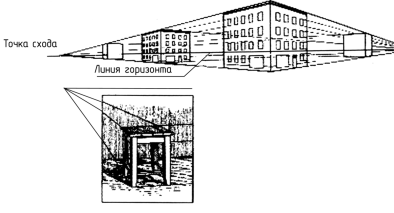
Рис. 2.6
Параллельное проецирование подразделяется на косоугольное и прямоугольное. При косоугольном проецировании проецирующие лучи наклонены к плоскости проекций, т.е. не равны 90° (рис. 2.7).
При прямоугольном проецировании проецирующие лучи идут к плоскости проекций под прямым углом, а полученная проекция называется прямоугольной (рис. 2.8). Метод прямоугольного проецирования используют при выполнении чертежей. Он позволяет наиболее точно и полно передать форму предметов.
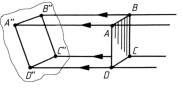
Рис. 2.7
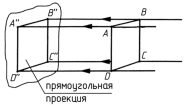
Рис. 2.8
Основы метода прямоугольного проецирования были разработаны французским ученым Гаспаром Монжем в конце XVIII в. Однако этот метод на практике использовался задолго до этого как в России, так и в других странах.
3. Какие основные свойства параллельного проецирования?
Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.
В зависимости от направления проецирующего луча по отношению к плоскости П' параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.
Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.
Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.
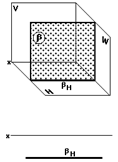
Горизонтальная плоскость
Горизонтальная плоскость (рис. 32) параллельна горизонтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.
a (aНа рис. 32 изображена горизонтальная плоскость V ).
Фронтальная плоскость
Фронтальная плоскость (рис. 33) параллельна фронтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.
| Рис. 32 | Рис. 33 |
b (bНа рис. 33 изображена фронтальная плоскость H ).
Профильная плоскость
Профильная плоскость (рис. 34) параллельна профильной плоскости проекций.
На двухкартинном комплексном чертеже она изображается двумя следами: горизонтальным и фронтальным, перпендикулярными оси x.
g (gНа рис. 34 изображена профильная плоскость H,V ).
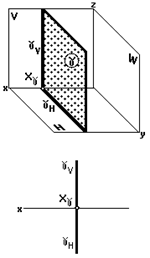
Рис. 34
Рис. 37
Профильные проекции всех точек, принадлежащих профильно-проецирующей g, располагаются на профильном следе —проекции этой gплоскости W плоскости (рис. 37).
31. Какие плоскости можно провести через фронтально проецирующую прямую.
Фронтально проецирующие прямые - прямые перпендикулярные фронтальной плоскости проекции.
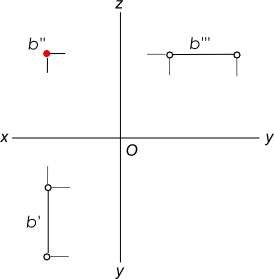
Проецирующие прямые
Эти прямые проецируются на плоскость V в точку, а их горизонтальные и профильные проекции параллельны оси y.
b⊥V
b" - точка, b` и b"` - прямые ║ y.
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
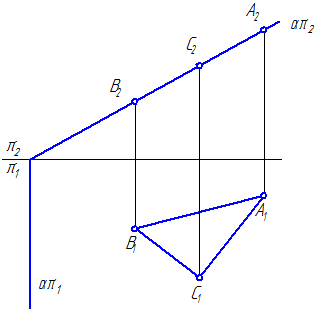
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
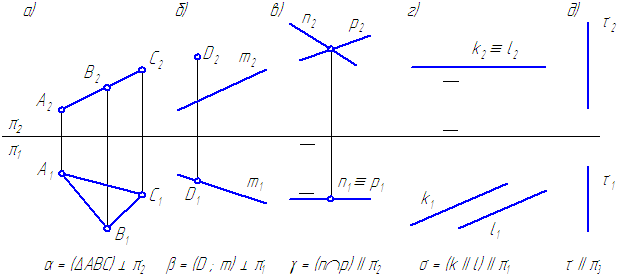
Рисунок 3.4 – Эпюры плоскостей частного положения
32. Какое условие принадлежности точки плоскости, прямой плоскости?
Точка принадлежит плоскости, если она принадлежит прямой этой плоскости. Прямая принадлежит плоскости, если она проходит через две точки этой плоскости.
Условия принадлежности точки прямой и прямой плоскости
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
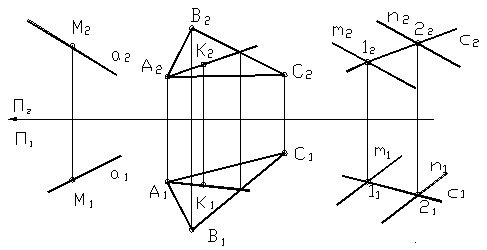
Рисунок 21
33. Какие линии относятся к особым (главным) линиям плоскости?
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
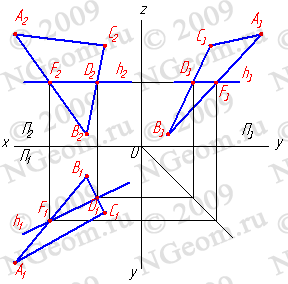
Рисунок 6.4 Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
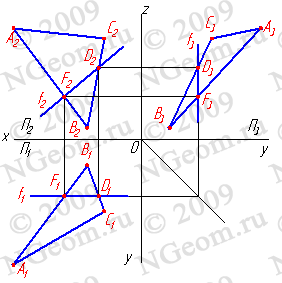
Рисунок 6.5 Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
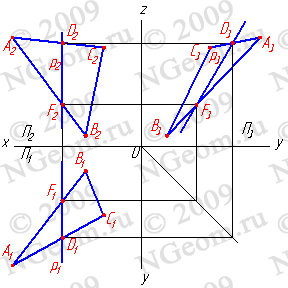
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
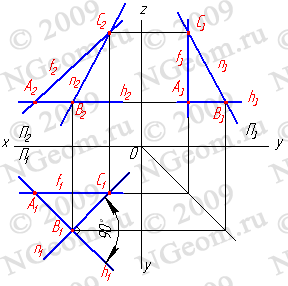
Рисунок 6.7 Линия наибольшего ската
34. Как построить проекции фронтали, горизонтали на чертеже?
Среди прямых, которые лежат в некоторой плоскости, можно выделить два класса прямых, играющих большую роль при решении всевозможных задач. Это прямые, которые называют горизонталями и фронталями.
Горизонталь плоскости Р (рис. 41) – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию г?, параллельную оси х.
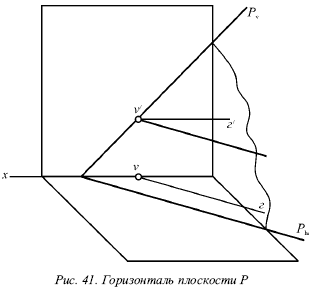
Три прямые – горизонталь Г, ее горизонтальная проекция г и горизонтальный след Ph плоскости Р – параллельны (рис. 42).
Действительно, горизонталь является прямой, параллельной горизонтальной плоскости, и поэтому не имеет горизонтального следа Ph, лежащего с ней в одной плоскости. При этом горизонталь Г не может пересечь свою горизонтальную проекцию г. В противном случае в этой точке пересечения она встречала бы горизонтальную плоскость, что противоречит определению, т. е. все три прямые Г, г и Ph параллельны.
Любая из плоскостей имеет множество горизонталей. Все горизонтали этой плоскости параллельны друг другу вследствие того, что все они параллельны прямой Ph.
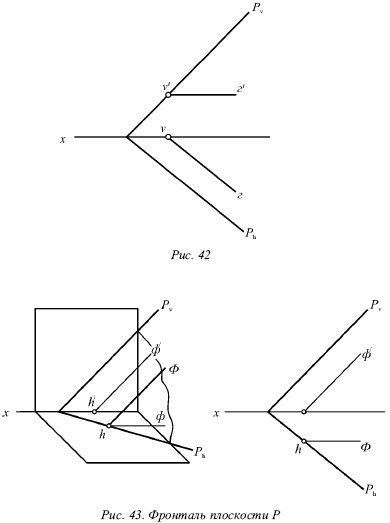
Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости (рис. 43).
Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекция ф параллельна оси х.
Фронталь Ф, ее фронтальная проекция ф? и фронтальный след Pv взаимно параллельны. У каждой плоскости есть бесчисленное множество фронталей. Все фронтали данной плоскости параллельны, за исключением плоскости, параллельной фронтальной плоскости.
35. Как может располагаться прямая линия относительно плоскости?
Прямая относительно плоскости может занимать различные положения:
1) прямая принадлежит плоскости(рассмотрено выше);
45
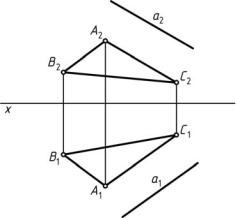
2) прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости:a |AC| α (∆АВС)a α (∆АВС) (рис. 35). Совокупность таких прямых образует в пространстве плоскость, параллельную заданной плоскости;
Рис. 35. Прямая, параллельнаяплоскости
3) прямая пересекается с плоскостью. Прямая пересекается с плоскостью в точке. Построить точку пересечения прямой с плоскостью — значит найти точку, принадлежащую одновременно заданной прямой и плоскости.
Рассмотрим примеры.
1. Прямая общего положения пересекается с плоскостью частного положения (рис. 36, а).
Плоскость α (АВС) —фронтально-проецирующаяплоскость, фронтальная проекция которой обладает собирательным свойством. Следовательно,K α (АВС) П2 K2 αΠ2 (А2В2С2). Видимость
прямой определяется методом конкурирующих точек.
2. Прямая частного положения пересекается с плоскостью общего положения (рис. 36, б).
Прямая c —горизонтально-проецирующаяпрямая. Следовательно,K c П1 K1 ≡c1. Для определения фронтальной проекции точкиK2 необходимо через горизонтальную проекцию точкиK1 провести проекцию любой прямой, принадлежащей плоскостиα (∆АВС), например,A1D1. Тогда|A2D2| ∩ c2 =K2. Видимость прямой определяется методом конкурирующих точек.
3. Прямая общего положения пересекается с плоскостью общего положения (рис. 36, в).
Для определения точки пересечения прямой l с плоскостьюα (∆АВС) применяют метод посредника, т. е. вводят вспомогательную секущую (проецирующую) плоскость. Например, прямуюl заключают
46
в плоскость частного положения β —фронтально-проецирующую.Определяют проекции линии пересечения двух плоскостейα (∆АВС)
иβ: фронтальную —D2E2, и горизонтальную —D1E1. Там, где горизонтальная проекцияD1E1 пересечет горизонтальную проекцию прямойl1,
ибудет точка K — точка пересечения прямойl и плоскостиα (∆АВС). Видимость прямой определяется методом конкурирующих точек.
| а | б | в |
Рис. 36. Пересечение прямой с плоскостью
Частным случаем пересечения прямой и плоскости является перпендикулярность этой прямой заданной плоскости.
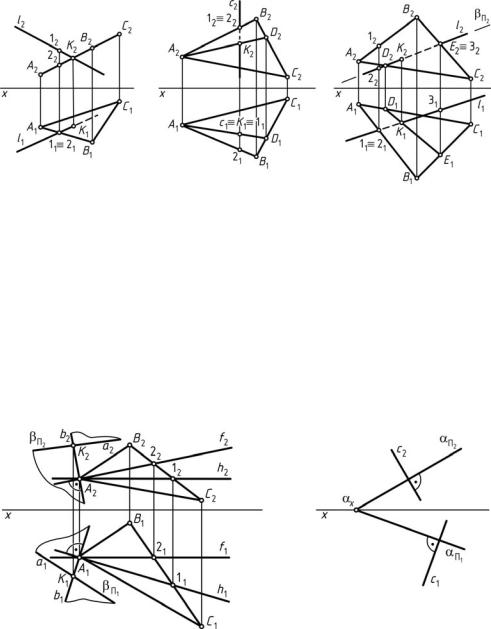
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости (рис. 37, а).
В качестве пересекающихся прямых, принадлежащих плоскости, используют горизонталь и фронталь данной плоскости.
Прямая перпендикулярна плоскости, заданной следами, если ее
проекции перпендикулярны одноименным следам этой плоскости
(рис. 37, б).
| а | б |
Рис. 37. Прямая, перпендикулярная плоскости
36. Как строят точку пересечения прямой линии с проецирующей плоскостью?
. Плоскость, перпендикулярная к плоскости проекций, проецируется на последнюю в виде прямой линии. На этой прямой (проекции плоскости) должна находиться соответствующая проекция точки, в которой некоторая прямая пересекает такую плоскость.
37. Как строят линию пересечения двух плоскостей, одна из которых проецирующая?
Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям.
38. Назвать этапы решения основной позиционной задачи?
Многогранники
Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником (рисунок 35).
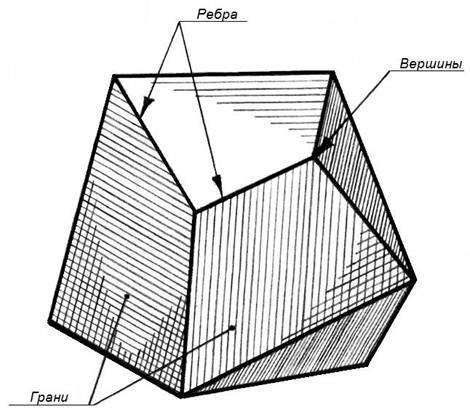
Рисунок 35 – Многогранник
Многогранники различают в зависимости от формы и количества граней.
Рассмотрим некоторые из многогранников, которые наиболее часто встречаются в технических чертежах.
Призма
Призма – многогранник, у которого две грани (основания) n-угольники, расположенные в параллельных плоскостях, а остальныеnграней (боковые грани) – параллелограммы. Призма может быть прямой, если боковые ребра перпендикулярны основанию (рисунок 36) и наклонной, если ребра не перпендикулярны основанию. Прямая призма называется правильной, если в основании у нее правильный многогранник.
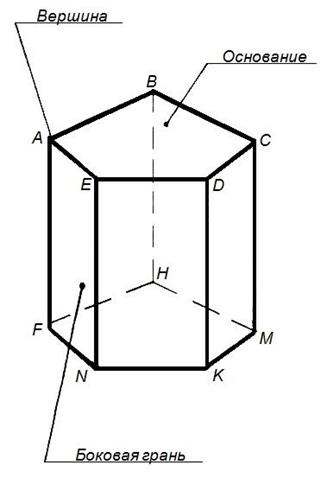
Рисунок 36 - Призма
Пирамида
Пирамида – многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину. В основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной (рисунок 37) и т.д.
При изображениях на комплексных чертежах многогранников принято считать, что их грани непрозрачные и поэтому проекции отдельных ребер и граней будут невидимы. При решении вопросов видимости принимается следующие правила (рисунок 38):
1. Линии, образующие внешний контур (очерк) каждой проекции, всегда видимы.
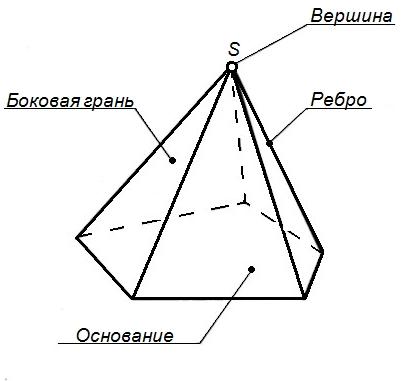
Рисунок 37 - Пирамида
2. Если внутри очерка пересекаются проекции двух ребер, то одна из них видимая, а другая невидимая (рисунок 38). Видимость определяется с помощью конкурирующих точек.
3. Если проекция хотя бы одного из ребер, ограничивающих грань, невидимая, то и вся грань невидимая.
4. На видимой грани лежат видимые элементы, на невидимой – невидимые.
5. Если в одной точке сходятся три или более ребер, то они все видимы или все невидимы.
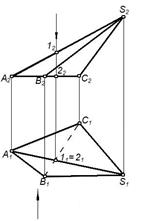
Рисунок 38 – Определение видимости пирамиды
42. Чем задается призматическая поверхность?
Призматическая поверхность- линейчатая поверхность, образованная параллельным перемещением прямой в пространстве (образующей) и пересекающей ломаную линию (направляющую).
Призматическая поверхность в пространстве и на чертеже задается своим определителем Ф (m; 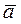 )[А]
)[А]
где m - направляющая;
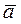 - направление перемещения образующей;
- направление перемещения образующей;
М Ì Ф - произвольная точка, принадлежащая поверхности призмы;
l || 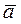 - образующая, проходящая через т.М;
- образующая, проходящая через т.М;
l É М и l ∩ m = 1М2 задана произвольно  М2 Î l2l2 || ā2 l2 ∩ m2 = 12 12 ® 11 и 11Î l1 l1 || ā1 М1 Î l1 М2 Î l2l2 || ā2 l2 ∩ m2 = 12 12 ® 11 и 11Î l1 l1 || ā1 М1 Î l1
| 
|
Рисунок 3.2
Т.к. М произвольная точка и вторая проекция ее построена, то теорема доказана.
Призма - геометрическая фигура, ограниченная замкнутой призматической поверхностью и двумя плоскостями.
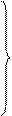 l ^ П1 l ^ П1  Г || П1 П1 Г || П1 П1
| 
|
Рисунок 3.3
43. Какие признаки позволяют установить, что на данном чертеже изображена призма?
Наличие на чертеже только прямолинейных отрезков, причем они служат проекциями или ребер, или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.
Положим, что нам известна по форме и положению фигура, полученная при пересечении всех боковых граней призмы плоскостью, и известно направление ребер призмы (рис. 258). Этим задается призматическая поверхность. Пересекая призматическую поверхность двумя параллельными между собой плоскостями, мы получаем основания призмы (рис. 258). Можно задаться одним из оснований призмы и ее высотой или длиной бокового ребра и тем задать призму.
Выбирая положение призмы для ее изображения, целесообразно располагать ее основания параллельно плоскости проекций.
Какие признаки позволяют установить, что на данном чертеже изображена именно призма (или, в частности, параллелепипед)? Наличие на чертеже только прямолинейных отрезков 2), причем они служат проекциями или ребер, или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.
1) Мы могли бы считать, что контуру тела в данном случае принадлежат и все точки отрезков АВ,ВС,DB1, B1D1, EF и E1F1 и даже площади треугольников АВС и DB1D1 и части трапеций EFF1E1, так как проецирующие плоскости α1; α2 и α3 проходят соответственно через эти фигуры.
Примеры даны на рис. 258 — 260: здесь в системе π1, π2 изображены прямая треугольная призма, наклонная четырехугольная призма и куб (о том, что это именно куб, свидетельствует равенство ребер и прямоугольность граней).

Но для тела, изображенного на рис. 261, несмотря на наличие некоторых из указанных выше признаков, было бы ошибочным утверждать, что это обязательно призма или параллелепипед. На рис. 261 справа показаны возможные варианты решений. Очевидно, в данном случае для уточнения следовало бы иметь профильную проекцию или обозначение вершин.
На рис. 262 изображена неправильная четырехугольная призма (основаниями служат трапеции). На рис. 263 (сверху) показано построение профильной проекции этой призмы с применением вспомогательной прямой. Там же (внизу) показано отнесение призмы к плоскостям координат, совпадающим с ее гранями. В этом случае третья проекция построена по координатам вершин.
44. Чем задается поверхность пирамиды?
Для задания поверхности пирамиды надо иметь фигуру сечение всех боковых граней пирамиды плоскостью и точку их пересечения. Обычно пирамида задается на чертеже проекциями ее основания и вершины, а усеченная пирамида – функциями обоих оснований. Выбирая положение пирамиды для ее изображения, целесообразно располагать основание параллельно плоскости проекций
45. При каком условии для изображения пирамиды достаточно двух проекций?
Для построения фигуры, получаемой при пересечении призмы и пирамиды плоскостью, надо или найти точки, в которых ребра призмы или пирамиды пересекают данную плоскость, или найти отрезки прямых, по которым грани призмы или пирамиды пересекаются плоскостью. В первом случае построение сводится к задаче на пересечение прямой с плоскостью, во втором случае — на пересечение плоскостей между собой.
В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид фигуры сечения 1), то следует применять один из способов, которые позволяют находить длину отрезка, величину угла и т. д. (см. главу V).
На рис. 273 показано пересечение прямой четырехугольной призмы плоскостью, заданной пересекающимися прямыми EF и EG. Обозначим эту плоскость буквой δ.
При пересечении получается четырехугольник, вершины которого представляют собой точки пересечения ребер призмы с пл.δ.Так как в данном случае призма прямая и основание ее параллельно пл. π1, то горизонтальная проекция фигуры сечения определяется сразу, без какого-либо построения: она накладывается на проекцию A'B'C'D'. Очевидно, можно найти точки К и L, в которых ребра призмы, проходящие через точки А и D, пересекают пл. δ, при помощи одной пл. α, в которой находится грань призмы α × δ = 1—2, откуда получаем точки К" и L".Проведя" пл. β, получим β × δ = 3 — 4 и точки М' и N'.
1) Выражение «натуральный вид сечения» мы будем применять в том случае, когда фигура сечения дается без искажения.
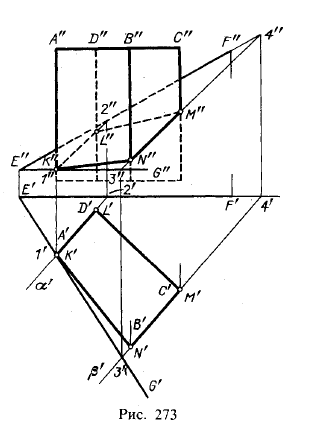
Итак, способ построения, который указан на рис. 273, сводится к применению вспомогательных плоскостей α и β, проходящих через соответствующие грани призмы, и построению отрезков KL и MN, по которым эти грани пересекаются пл. δ.
На фронтальной проекции линия пересечения состоит из видимой и невидимой частей; видимая часть линии пересечения расположена на обращенных к зрителю видимых гранях.
На рис. 273 находящаяся под пл. δ нижняя часть призмы представлена как невидимая. Линия пересечения лишь прочерчена на гранях призмы.
Если секущая плоскость перпендикулярна к одной из плоскостей проекций (рис. 274, слева), то проекции фигуры сечения получаются без каких-либо дополнительных проекция K"P"M"N" располагается на следе β", горизонтальная проекция K'P'N'M' совпадает с проекцией призмы.
На рис. 274 справа показано пересечение призмы пл. α, заданной пересекающимися прямыми АВ и ВМ2, из которых ВМ2 параллельна ребрам призмы. Следовательно, секущая плоскость в данном случае общего положения, параллельная
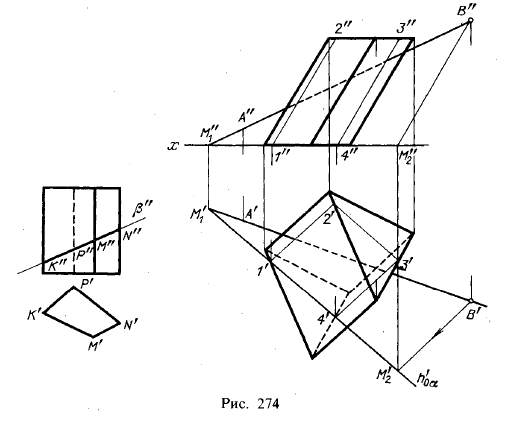
ребрам призмы. Она пересекает призмы по параллелограмму 1 — 2 — 3 — 4, стороны 1 — 2 и 3 — 4 которого параллельны ребрам призмы. Чтобы провести эти стороны, надо построить след пл. α на плоскости основания призмы и пересечь им это основание по прямой 1—4.
На рис. 275 показано пересечение пирамиды плоскостью общего положения α, выраженной следами. Дело сводится к нахождению точек пересечения ребер SA, SB и SC с пл. α, т. е. к задаче на пересечение прямой с плоскостью (см. § 25). Рассмотрим нахождение точки L, в которой ребро SB пересекает пл. α. Выполняем следующие действия: 1) через SB проводим вспомогательную плоскость, в данном случае горизонтально-проецирующую β; 2) находим прямую пересечения 1—2 плоскостей α и β; 3) находим точку L в пересечении прямых SB и 1 — 2.
Далее, так как в данном случае ребро SA расположено параллельно пл. π2, проводим через него вспомогательную фронтальную плоскость δ. Она пересекает пл. α
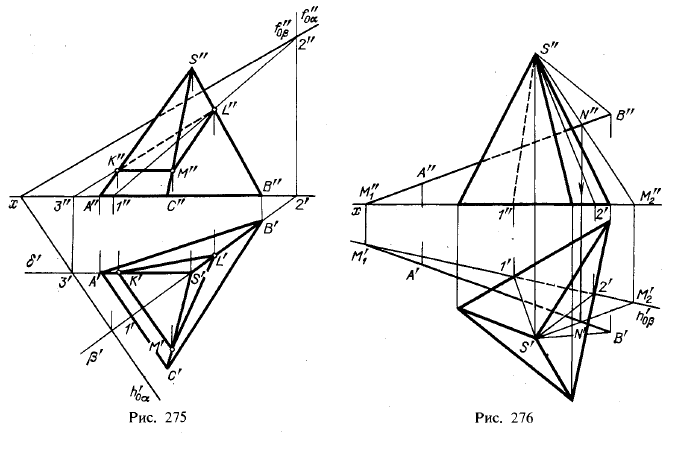
по ее фронтали с начальной точкой 3; в пересечении этой фронтали с ребром SA получаем точку К.
Теперь обратим внимание на другую особенность в данном примере: проекция А'С' параллельна следу h'0α. Это тот случай, когда у двух плоскостей горизонтальные следы взаимно параллельны (h'0α|| А'С', но А'С' — часть горизонтального следа плоскости грани SAC) и линия пересечения таких плоскостей является их общей горизонталью. Поэтому мы можем провести через уже найденную точку К прямую, параллельную ребру АС (или ||h'0α, и так найти точку М.
Если бы не было этих особенностей, то следовало бы поступать аналогично построению точки L.
Чертеж на рис. 275 выполнен согласно условию, что пл. α прозрачна и что основным является нанесение на гранях линий разделения пирамиды на две части.
Пусть (рис. 276) пирамида рассечена пл. α, заданной пересекающимися прямыми АВ и SB, причем SB проходит через вершину пирамиды. Следовательно, пл. α рассекает ее по треугольнику, одна из вершин которого находится в точке S. Чтобы найти две другие вершины треугольника — точки 1 и 2, надо построить след пл. α на плоскости основания пирамиды. Остальное ясно из чертежа.
При пересечении поверхности призмы или пирамиды прямой линией получаются две точки. Для них встречается название точки входа и выхода. Чтобы найти эти точки, надо провести через данную прямую вспомогательную плоскость и найти линии ее пересечения с гранями; эти линии на гранях оказываются расположенными в одной плоскости с данной прямой и в своем пересечении дают точки, в которых данная прямая пересекает поверхность.
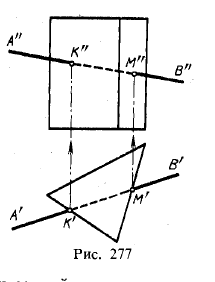
Могут быть случаи, когда нет надобности в таких построениях. Пример дан на рис. 277; положение проекций К' и М' очевидно, так как боковые грани призмы перпендикулярны к пл. π1. По точкам К' и М' найдены точки К" и М".
На рис. 278 показано построение точек пересечения прямой линии с поверхностью пирамиды. Через прямую АВ проведена вспомогательная фронтально-проецирующая пл. α. Фронтальная проекция фигуры сечения пирамиды этой плоскостью сливается с фронтальной проекцией плоскости; горизонтальная проекция сечения найдена построением. Точки пересечения горизонтальной проекции прямой АВ с горизонтальной проекцией фигуры сечения представляют собой горизонтальные проекции искомых точек; по найденным горизонтальным проекциям (точки К' и М') построены фронтальные проекции (К" и М") точек пересечения.
----------
Построение точек пересечения прямой линии с поверхностью призмы можно представить себе еще следующим образом. Положим, что мы вместо прямоугольного проецирования применим косоугольное. Спроецируем призму и прямую АВ (рис. 279) на пл. π1 по направлению, параллельному ребрам данной призмы. Призма спроецируется в треугольник C1D1E1, совпадающий е горизонтальной
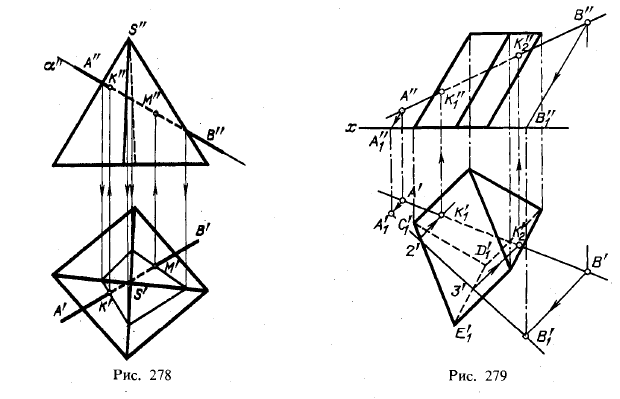
проекцией нижнего основания призмы, а прямая АВ — в прямую А1В1, которая пересечет стороны треугольника C1D1E1 в точках 2 и 3. Обратным проецированием мы получим проекции К'1 и К'2, а по ним К"1 и К"2.
46. В какой последовательности строят проекции правильной шестигранной призмы, основания которых расположены на профильной плоскости проекций?
Построение проекций правильной прямой призмы (рисунок 127) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Так как основание призмы параллельно горизонтальной плоскости проекций H, то эта проекция изображается отрезком прямой параллельно оси OX. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых (т.к. они перпендикулярны горизонтальной плоскости проекций). Передняя боковая грань 1243 изображается на фронтальной плоскости проекций V без искажения, а на плоскости H — в виде прямой линии. Фронтальные и профильные проекции остальных граней изображаются с искажением.
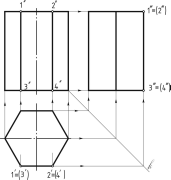
Рисунок 127
На чертеже оси х, у и z не показывают, что делает чертеж более простым.
47. Чем отличается призма от пирамиды?
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена. Пирами́да (др. -греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину [1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.
Рассмотрим прямую призму, которая стоит на горизонтальной плоскости (рис. 56).
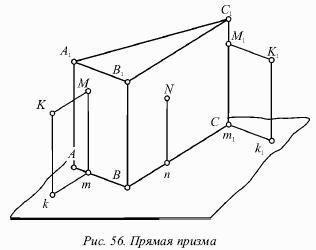
Ее боковые грани являются частями горизонтально-проецирующих плоскостей, а ребра являются отрезками вертикальных прямых. Исходя из этого ребра следует проецировать на горизонтальную плоскость в виде точек, а на фронтальную плоскость – без искажения (АА = а́а́1 и т. д.).
Нижнее основание призмы АВС находится в горизонтальной плоскости, поэтому ее можно изобразить на этой плоскости без искажения: ΔАВС = Δаbс. Фронтальная проекция пирамиды а́b́с́ совпадает с осью х.
Оба основания дают одинаковые горизонтальные проекции (Δаbс = Δа1b1с1). Верхнее основание А1В1С1 параллельно горизонтальной плоскости, т. е. его фронтальная проекция а́1b́1с́1 параллельна оси х.
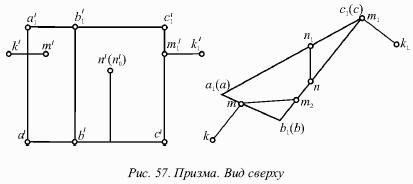
При рассмотрении призмы сверху (рис. 57) будет видно только верхнее основание призмы.
Горизонтальные проекции трех точек, которые лежат на нижнем основании, помещены в скобки с целью показа, того, что точки А, В и С невидимы, если смотреть на призму из данного положения.
Для определения невидимых элементов на фронтальной проекции обращаются к горизонтальной проекции.
Направление луча зрения показано на рисунке 58 стрелкой. Видно, что грань АА1С1С при таком угле зрения будет невидимой.
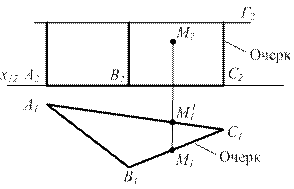
На рисунке 58 показана треугольная пирамида, которая находится на горизонтальной плоскости.

Гранями пирамиды являются треугольники, являющиеся частями плоскостей общего положения.
Если рассматривать пирамиду сверху, можно увидеть всю ее боковую поверхность, т. е. для горизонтальной проекции не существует невидимых элементов.
Из рассуждений, подобных рассуждениям в случае призмы, можно убедиться, что на фронтальной проекции невидима грань SАС (рис. 59).
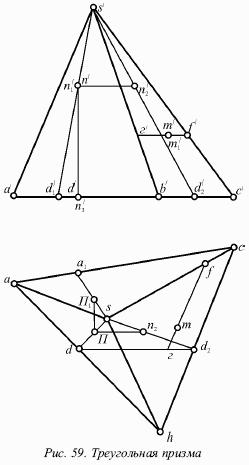
Рис. 2.5
екции используются при выполнении перспективных рисунков предметов, сооружений и др. (рис. 2.6).
Если центр проецирования удалить в бесконечность, то все проецирующие лучи будут параллельны друг другу. Такой метод проецирования называется параллельным, а полученная проекция — параллельной. В природе примером параллельного проецирования являются солнечные или лунные тени.

Рис. 2.6
Параллельное проецирование подразделяется на косоугольное и прямоугольное. При косоугольном проецировании проецирующие лучи наклонены к плоскости проекций, т.е. не равны 90° (рис. 2.7).
При прямоугольном проецировании проецирующие лучи идут к плоскости проекций под прямым углом, а полученная проекция называется прямоугольной (рис. 2.8). Метод прямоугольного проецирования используют при выполнении чертежей. Он позволяет наиболее точно и полно передать форму предметов.

Рис. 2.7

Рис. 2.8
Основы метода прямоугольного проецирования были разработаны французским ученым Гаспаром Монжем в конце XVIII в. Однако этот метод на практике использовался задолго до этого как в России, так и в других странах.
3. Какие основные свойства параллельного проецирования?
Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.
В зависимости от направления проецирующего луча по отношению к плоскости П' параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.
Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.
Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.
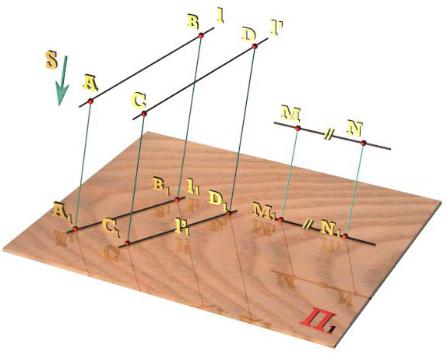
Свойства параллельного проецирования
1.Проекция точки – точка.
2.Проекция прямой в общем случае – прямая.
3.Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии.
4.Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых.
Свойства параллельного проецирования
5.Проекции взаимно параллельных прямых взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
6.Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость без искажения.
4. Может ли параллельная проекция прямой линии представлять собой точку?
Да, если направление прямой линии совпадает с направлением проецирования. Параллельная проекция прямой линии может представлять собой точку, когда эта прямая параллельна направлению проецирования (сонаправлена с направлением проецирования).
5. Что такое Эпюр Монжа?
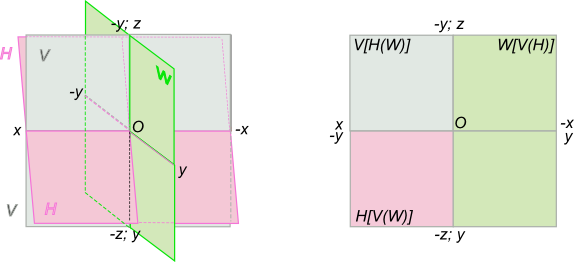
Эпюра Монжа или комплексный чертеж - это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры.
Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.
Эпюра Монжа получается преобразованием пространственного макета путем совмещения плоскостей H и W с фронтальной плоскостью проекций V:
- для совмещения плоскости H с V поворачиваем ее на 90 градусов вокруг оси x в направлении движения часовой стрелки. На рисунке, для наглядности, плоскость H повернута на угол чуть меньший 90 градусов, при этом ось y, принадлежащая горизонтальной плоскости проекции, после поворота совпадает с осью z;
- после совмещения горизонтальной плоскости, поворачиваем вокруг оси z также на угол 90 градусов профильную плоскость в направлении противоположном движению часовой стрелки. При этом ось y, принадлежащая профильной плоскости проекции, после поворота совпадает с осью x.
Эпюра Монжа
После преобразования пространственный макет примет вид, показанный на рисунке. На этом рисунке указана также последовательность взаимного положения пол плоскостей проекций, так запись V[H(W)] указывает, что в этой части эпюра Монжа (ограниченного положительным направлением осей x и z) ближе к нам находится верхняя левая пола фронтальной плоскости проекции V, за ней располагается задняя левая пола горизонтальной плоскости проекции H, далее следует верхняя задняя пола профильной плоскости W.
Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке.
Эпюра Монжа
Эпюра Монжа может быть выполнена с помощью:
- обычных чертежных инструментов и приспособлений:
Чертежные инструменты;
Чертежные принадлежности и приборы;
- Программы для построения (рисования) эпюра Монжа: Выполнение чертежа в графическом редакторе.
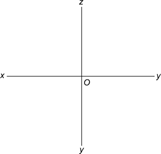
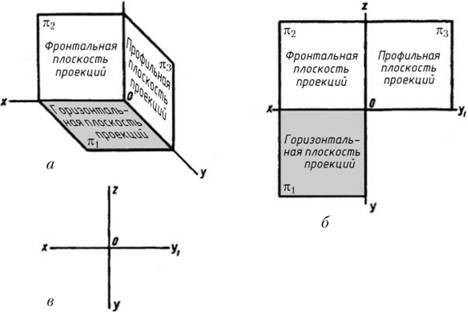
6. Как называются и обозначаются плоскости проекций?
Чтобы получить полное представление о форме и габаритах предмета, надо отобразить его на двух, трех или более плоскостях. Чтобы упростить процесс проецирования, плоскости располагают взаимно перпендикулярно. 3 взаимно перпендикулярные плоскости образуют прямой трехгранный угол.
Каждая плоскость имеет название:
• Фронтальная плоскость проекции располагается перед нами (вид спереди) и обозначается буквой - П2 или латинской V.
• Горизонтальная плоскость проекции располагается под прямым углом к фронтальной плоскости (вид сверху) и обозначается буквой П1 или латинской H.
• Профильная плоскость располагается перпендикулярно к обеим плоскостям (вид сбоку) и обозначается буквой П3 или латинской W.
При образовании трехгранного угла образуются прямые линии – оси проекции, которые обозначаются латинскими буквами – x, y,z, исходящие из точки О.
7. Что называют осью проекций и линией связи на чертеже?
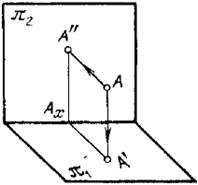 Ось проекций - это
Ось проекций - это
линия пересечения плоскостей проекций называется осью проекций. Ось проекций разделяет каждую из плоскостей п1 и п2 на полуплоскости.
Линия проекционной связи - это прямая, связывающая пары проекций одной и той же точки, и перпендикулярная оси проекций.
8. Какими координатами определяется фронтальная A2 проекция точки A? Горизонтальная A1 проекция точки A? Профильная A3 проекция точки A?
Дата: 2019-03-05, просмотров: 1196.