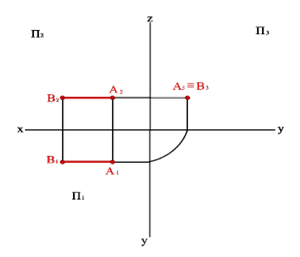
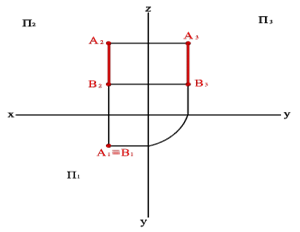
Прямой угол проецируется на горизонтальную, фронтальную и профильную плоскости проекций без искажения, если он образован двумя пересекающимися или скрещивающимися прямыми линиями. Одна из ко-

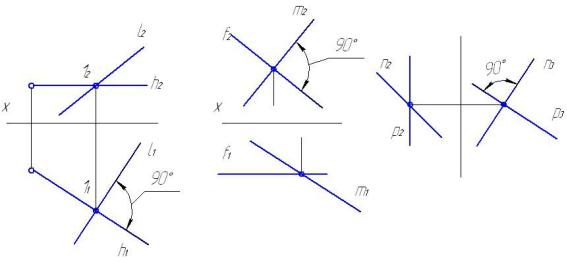
торых является соответственно горизонтальной, фронтальной или профильной линиями уровня, а вторая – составляет с соответствующей плоскостью проекций любой угол, кроме прямого (рисунок 2.13).

Рисунок 2.13 – Проекции прямого угла

\графический признак изображения прямого угла на эпюре- Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью

19. Что называется следом прямой?

Следом прямой называют точку пересечения прямой с плоскостью проекций. Прямая общего положения пересекается со всеми тремя плоскостями проекций и имеет три следа. Прямая, параллельная одной плоскости проекций, имеет два следа. Прямая, параллельная двум плоскостям проекций (проецирующая), имеет один след. М - горизонтальный след, N –фронтальный след. Там, где отрезок АВ пересекается с горизонтальной плоскостью проекций, получаем горизонтальный след М. Фронтальный след N получаем при пересечении отрезка АВ с фронтальной плоскостью проекции. Профильный след рассматривать в задачах не будем (рис. 29).

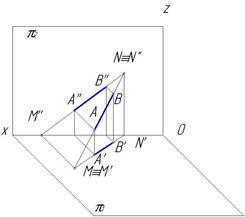Рис.29

След прямой - это точка, лежащая на плоскости проекций и самой прямой одновременно. Если точка лежит на плоскости, то одна ее проекция совпадает с самой точкой, а вторая обязательно лежит на оси х.

Для построения следов прямой АВ на эпюре поступают следующим образом: продолжают А''В" до пересечения с осью х и отмечают фронтальную проекцию М", из М" восстанавливают перпендикуляр до пересечения с А'В' или ее продолжением. Получаем горизонтальный след М' и сам след М.

При продолжении А'В' до пересечения с осью х получаем горизонтальную проекцию N' фронтального следа. Из N' восстанавливаем _┴ до пересечения с А"В" или ее продолжением для получения фронтального следа N". N" совпадает с фронтальным следом N (рис.30). В наших примерах мы рассматриваем только горизонтальные и фронтальные следы прямых.

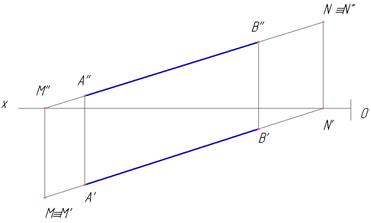Рис.30

Два следа прямой вполне определяют положение прямой в пространстве. По следам прямой можно определить через какие четверти пространства она проходит, если отрезок прямой продолжить в обе стороны. До следа N прямая проходит через I четверть, между следами М и N - II четверть, за следом М - III четверть. Можно записать: прямая, заданная отрезком АВ, проходит через I-II-III четверти (рис.31)

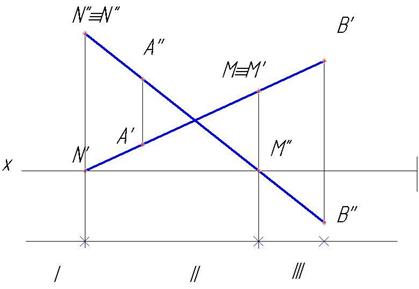Рис.31

20. Какими элементами определяется прямая в пространстве и на эпюре.

Прямые в пространстве могут быть: параллельными, пересекающимися и скрещивающимися.

Если прямые в пространстве параллельны, то на эпюре их одноименные проекции параллельны (рисунок 5.5).

Рисунок 5.5 – Эпюр параллельных прямых

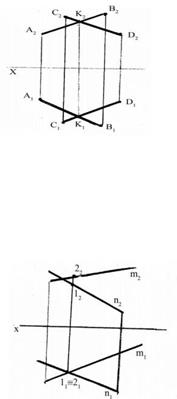
Если прямые в пространстве пересекаются, то на эпюре их одноименные проекции пересекаются и проекции точки пересечения К располагаются на одной вертикальной линии связи (рисунок 5.6).

Рисунок 5.6 – Эпюр пересекающихся прямых

Если в пространстве прямые скрещиваются, то на эпюре точки кажущегося пересечения не лежат на одной вертикальной линии связи. Эти точки (1 и 2) называются конкурирующими и по ним определяется видимость объектов. На рисунке 5.7 точка 2 расположена выше точки 1.

Рисунок 5.7 – Эпюр скрещивающихся прямых

21. Как могут располагаться прямые линии относительно плоскостей проекций?

Положение прямой относительно плоскостей проекций. Классификация прямых

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения(рис.1).

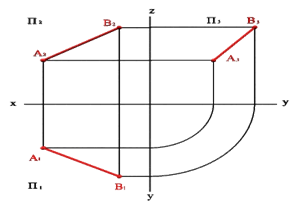
Рисунок 1. Прямая общего положения.

Эпюрный признак прямой общего положения: проекции прямой не параллельны осям проекций (x,y,z)

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

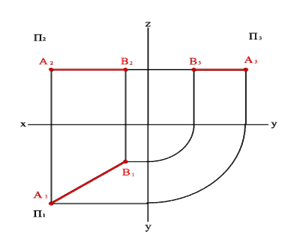
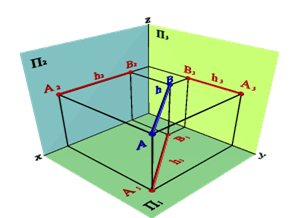
2.1. Прямые параллельные горизонтальной плоскости проекций называютсягоризонтальнымиилигоризонталями(рис.2). На горизонтальную плоскость проекций они проецируются в натуральную величину..

Эпюрный признак горизонтали

Проекция A₂B₂//x, проекция A₃B₃//y, проекция- A₁B₁ натуральная величина

а) модель		б) эпюр
Рисунок 2. Горизонталь

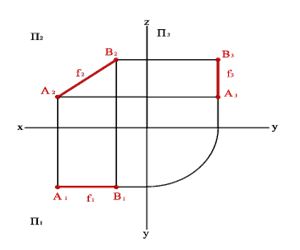
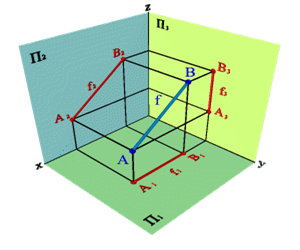
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными илифронталями(рис.3).Эпюрный признакфронтали

Проекция A₁B₁//x, проекция A₃B₃//z, проекцияA₂B₂- натуральная величина

а) модель		б) эпюр

Рисунок 3. Фронталь

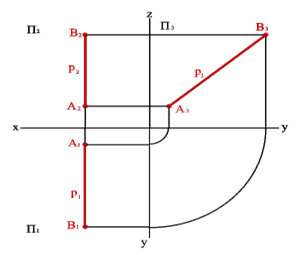
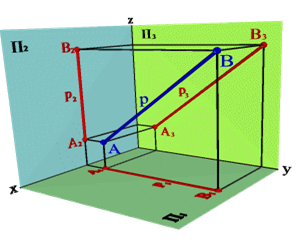
2.3. Прямые параллельные профильной плоскости проекций называются профильными(рис.4). Эпюрный признакпрофильной прямой

Проекция A₁B₁//y, проекция A₂B₂//z проекция A₃B₃- натуральная величина,

а) модель		б) эпюр

Рисунок 4 . Профильная прямая

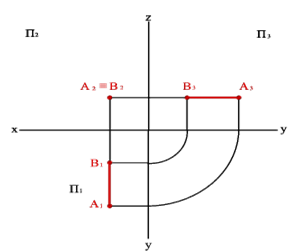
3. Прямые перпендикулярные плоскостям проекций, называютсяпроецирующими.Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

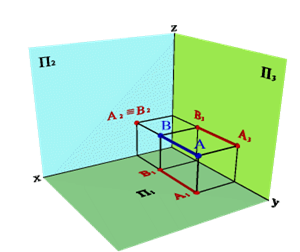
3.1. Фронтально проецирующаяпрямая -АВ .рис.(5)

а) модель		б) эпюр

Рисунок 5. Фронтально проецирующая прямая

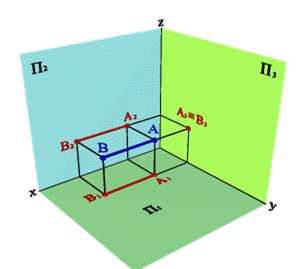
3.2. Профильно проецирующаяпрямая - АВ (рис.6)

а) модель		б) эпюр
Рисунок 6. Профильно-проецирующая прямая

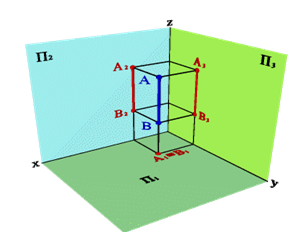
3.3. Горизонтально проецирующая прямая - АВ (рис.7)

а) модель		б) эпюр

Рисунок 7. Горизонтально-проецирующая прямая