ПРОЕЦИРУЮЩИМИ называются плоскости, перпендикулярные к плоскостям проекций.
Характерной особенностью таких плоскостей является их собирательное свойство. Оно заключается в следующем: соответствующий след — проекция плоскости — собирает одноименные проекции всех элементов, расположенных в данной плоскости.
Горизонтально-проецирующая плоскость
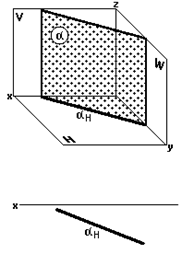
Горизонтально-проецирующая плоскость (рис. 33) перпендикулярна к горизонтальной плоскости проекций H.
| 
|
| Рис. 35 | Рис. 36 |
Горизонтальные проекции всех точек, принадлежащих , располагаются на горизонтальномaгоризонтально-проецирующей плоскости aследе — проекции H этой плоскости (рис. 35).
Фронтально-проецирующая плоскость
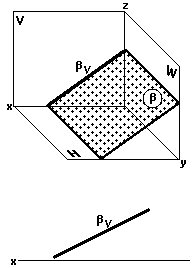
Фронтально-проецирующая плоскость (рис. 36) перпендикулярна к фронтальной плоскости проекций V.
Фронтальные проекции всех точек, принадлежащих , располагаются на фронтальном следе —bфронтально-проецирующей плоскости bпроекции H этой плоскости (рис. 36).
Профильно-проецирующая плоскость
Профильно-проецирующая плоскость (рис. 37) перпендикулярна к профильной плоскости проекций W.
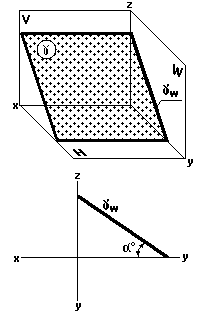
Рис. 37
Профильные проекции всех точек, принадлежащих профильно-проецирующей g, располагаются на профильном следе —проекции этой gплоскости W плоскости (рис. 37).
31. Какие плоскости можно провести через фронтально проецирующую прямую.
Фронтально проецирующие прямые - прямые перпендикулярные фронтальной плоскости проекции.
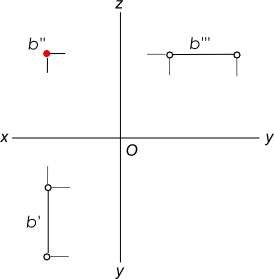
Проецирующие прямые
Эти прямые проецируются на плоскость V в точку, а их горизонтальные и профильные проекции параллельны оси y.
b⊥V
b" - точка, b` и b"` - прямые ║ y.
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
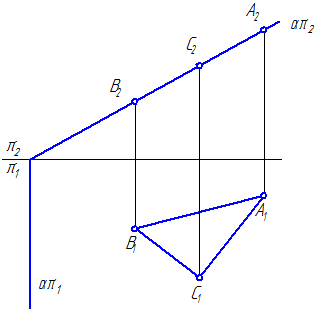
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
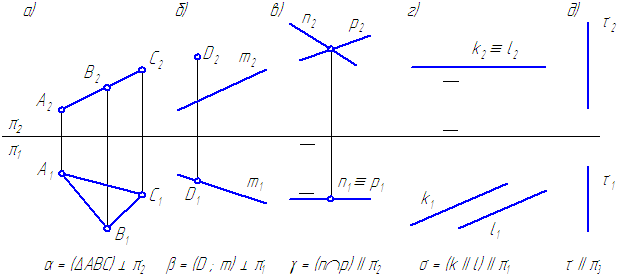
Рисунок 3.4 – Эпюры плоскостей частного положения
32. Какое условие принадлежности точки плоскости, прямой плоскости?
Точка принадлежит плоскости, если она принадлежит прямой этой плоскости. Прямая принадлежит плоскости, если она проходит через две точки этой плоскости.
Условия принадлежности точки прямой и прямой плоскости
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
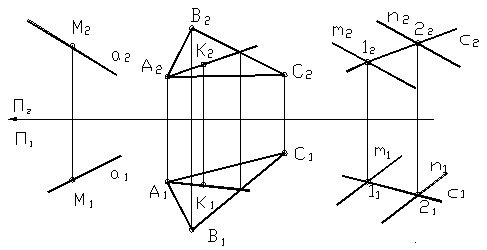
Рисунок 21
33. Какие линии относятся к особым (главным) линиям плоскости?
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
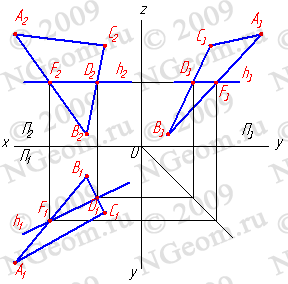
Рисунок 6.4 Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
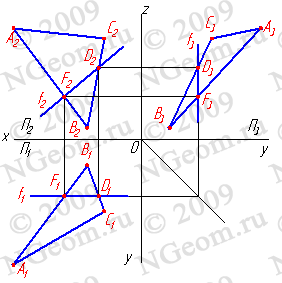
Рисунок 6.5 Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
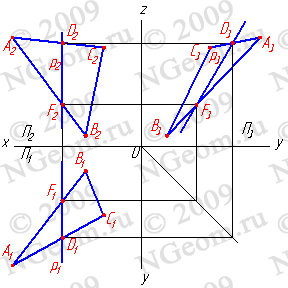
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
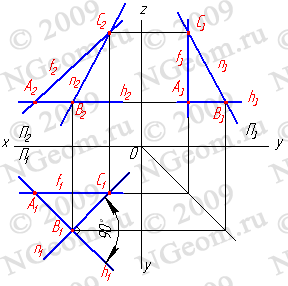
Рисунок 6.7 Линия наибольшего ската
34. Как построить проекции фронтали, горизонтали на чертеже?
Среди прямых, которые лежат в некоторой плоскости, можно выделить два класса прямых, играющих большую роль при решении всевозможных задач. Это прямые, которые называют горизонталями и фронталями.
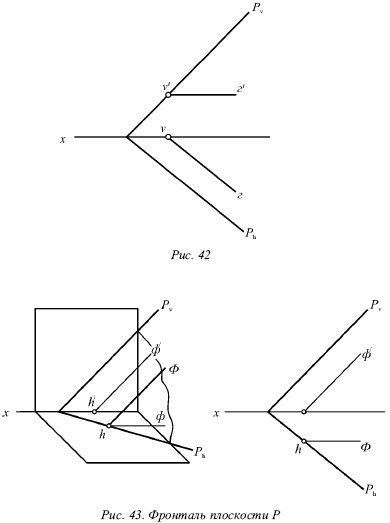
Горизонталь плоскости Р (рис. 41) – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию г?, параллельную оси х.
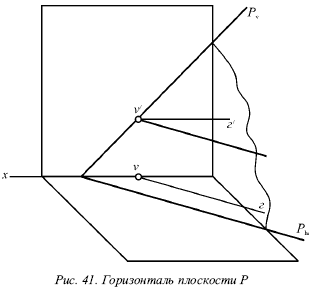
Три прямые – горизонталь Г, ее горизонтальная проекция г и горизонтальный след Ph плоскости Р – параллельны (рис. 42).
Действительно, горизонталь является прямой, параллельной горизонтальной плоскости, и поэтому не имеет горизонтального следа Ph, лежащего с ней в одной плоскости. При этом горизонталь Г не может пересечь свою горизонтальную проекцию г. В противном случае в этой точке пересечения она встречала бы горизонтальную плоскость, что противоречит определению, т. е. все три прямые Г, г и Ph параллельны.
Любая из плоскостей имеет множество горизонталей. Все горизонтали этой плоскости параллельны друг другу вследствие того, что все они параллельны прямой Ph.
Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости (рис. 43).
Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекция ф параллельна оси х.
Фронталь Ф, ее фронтальная проекция ф? и фронтальный след Pv взаимно параллельны. У каждой плоскости есть бесчисленное множество фронталей. Все фронтали данной плоскости параллельны, за исключением плоскости, параллельной фронтальной плоскости.
35. Как может располагаться прямая линия относительно плоскости?
Прямая относительно плоскости может занимать различные положения:
1) прямая принадлежит плоскости(рассмотрено выше);
45
2) прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости:a |AC| α (∆АВС)a α (∆АВС) (рис. 35). Совокупность таких прямых образует в пространстве плоскость, параллельную заданной плоскости;
Рис. 35. Прямая, параллельнаяплоскости
3) прямая пересекается с плоскостью. Прямая пересекается с плоскостью в точке. Построить точку пересечения прямой с плоскостью — значит найти точку, принадлежащую одновременно заданной прямой и плоскости.
Рассмотрим примеры.
1. Прямая общего положения пересекается с плоскостью частного положения (рис. 36, а).
Плоскость α (АВС) —фронтально-проецирующаяплоскость, фронтальная проекция которой обладает собирательным свойством. Следовательно,K α (АВС) П2 K2 αΠ2 (А2В2С2). Видимость
прямой определяется методом конкурирующих точек.
2. Прямая частного положения пересекается с плоскостью общего положения (рис. 36, б).
Прямая c —горизонтально-проецирующаяпрямая. Следовательно,K c П1 K1 ≡c1. Для определения фронтальной проекции точкиK2 необходимо через горизонтальную проекцию точкиK1 провести проекцию любой прямой, принадлежащей плоскостиα (∆АВС), например,A1D1. Тогда|A2D2| ∩ c2 =K2. Видимость прямой определяется методом конкурирующих точек.
3. Прямая общего положения пересекается с плоскостью общего положения (рис. 36, в).
Для определения точки пересечения прямой l с плоскостьюα (∆АВС) применяют метод посредника, т. е. вводят вспомогательную секущую (проецирующую) плоскость. Например, прямуюl заключают
46
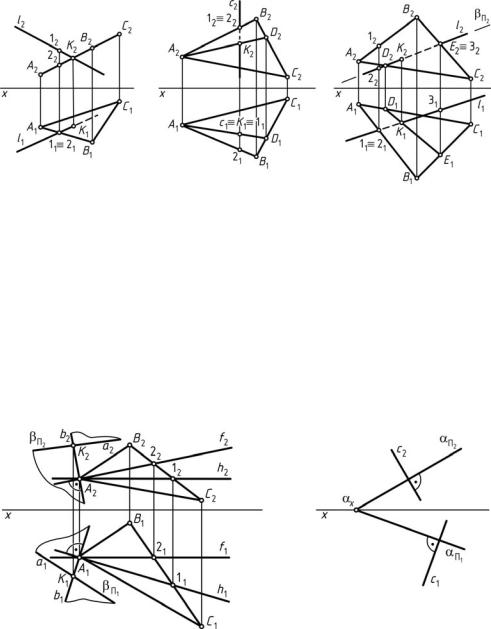
в плоскость частного положения β —фронтально-проецирующую.Определяют проекции линии пересечения двух плоскостейα (∆АВС)
иβ: фронтальную —D2E2, и горизонтальную —D1E1. Там, где горизонтальная проекцияD1E1 пересечет горизонтальную проекцию прямойl1,
ибудет точка K — точка пересечения прямойl и плоскостиα (∆АВС). Видимость прямой определяется методом конкурирующих точек.
| а | б | в |
Рис. 36. Пересечение прямой с плоскостью
Частным случаем пересечения прямой и плоскости является перпендикулярность этой прямой заданной плоскости.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости (рис. 37, а).
В качестве пересекающихся прямых, принадлежащих плоскости, используют горизонталь и фронталь данной плоскости.
Прямая перпендикулярна плоскости, заданной следами, если ее
проекции перпендикулярны одноименным следам этой плоскости
(рис. 37, б).
| а | б |
Рис. 37. Прямая, перпендикулярная плоскости
36. Как строят точку пересечения прямой линии с проецирующей плоскостью?
. Плоскость, перпендикулярная к плоскости проекций, проецируется на последнюю в виде прямой линии. На этой прямой (проекции плоскости) должна находиться соответствующая проекция точки, в которой некоторая прямая пересекает такую плоскость.
37. Как строят линию пересечения двух плоскостей, одна из которых проецирующая?
Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям.
38. Назвать этапы решения основной позиционной задачи?
Дата: 2019-03-05, просмотров: 711.