Параллельные прямые лежат в одной плоскости, никогда не пересекаются, и на всем протяжении расстояние между ними одинаково.

Пересекающиеся прямые лежат в одной плоскости и имеют только одну общую точку.

Скрещивающиеся прямые не лежат в одной плоскости, они никогда не пересекаются и они не параллельны.

Рассмотрим построение проекций для каждого из этих случаев расположения прямых в пространстве.

1. Пусть даны две прямые параллельные линии общего положения (т.е. они не параллельны и не перпендикулярны ни одной из плоскостей проекций). Следует помнить, что одноименные проекции параллельных прямых всегда параллельны. В общем случае справедливо и обратное, т.е. если на трех плоскостях проекций одноименные проекции параллельны, то изображаемые линии параллельны и в пространстве.

Если одноименные проекции параллельны только на одной или двух плоскостях проекций, то нельзя однозначно считать, что изображаемые линии параллельны в пространстве.

Если параллельны одноименные проекции прямых на двух плоскостях проекций, то сами прямые параллельны в пространстве только в том случае, если они являются прямыми общего положения.

Если имеются две прямые частного положения, параллельные одной и той же плоскости проекций, например горизонтальной, то даже если параллельны фронтальная и профильная проекции этих линий, сами прямые будут параллельны только при условии, что параллельны их горизонтальные проекции. Следовательно, для однозначного определения положения прямых в пространстве требуется построить их горизонтальные проекции.

Проекции параллельных линий можно построить или по общему правилу построения проекций прямой общего положения, или следующим образом: по общему правилу строят проекции одной из параллельных прямых и проекции какой-либо точки второй параллельной прямой, затем через полученные проекции точек на каждой из плоскостей проекций проводят линии, параллельные соответствующим проекциям первой из параллельных прямых, которые и будут являться проекциями второй параллельной прямой.

2. Пусть имеются две пересекающиеся прямые ЛВ и CD ( т.е. они лежат в одной плоскости), и пусть т. Е — точка их пересечения. В этом случае будут пересекаться и одноименные проекции прямых Л В' и C'D', А" В" и C"D" , причем точки пересечения проекций будут проекциями т. Е— соответственно т. Е' и т. Е".

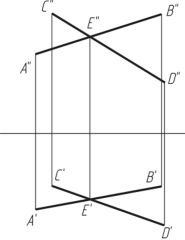
Рис. 2.6

Если известно, что пересекаются одноименные проекции прямых на двух плоскостях проекций, то однозначно утверждать, что пересекаются и сами прямые в пространстве, можно лишь тогда, когда точка пересечения одноименных проекций находится на одном и том же перпендикуляре к соответствующей оси проекций (для прямых общего положения) (рис. 2.6).

Если пересекающиеся прямые — прямые частного положения, то картина иная. Например, если обе пересекающиеся прямые параллельны какой-нибудь плоскости проекций, пусть горизонтальной, то пересекающимися будут только их горизонтальные проекции, а проекции на другие плоскости проекций сольются.

Если прямые ЛВ и CD пересекаются под углом 90°, то совсем не обязательно, что под таким же углом будут пересекаться их одноименные проекции. Угол пересечения их проекций на эту плоскость будет прямой только при условии, что одна из прямых параллельна плоскости проекций.

3. Пусть имеются две скрещивающиеся прямые АВ и CD. Хотя эти прямые не пересекаются в пространстве, их одноименные проекции могут пересекаться, но в отличие от случая пересекающихся прямых точки пересечения их одноименных проекций не располагаются на общем перпендикуляре к оси координат. Иногда одноименные проекции скрещивающихся прямых параллельны, но не на всех плоскостях проекций, на одной из плоскостей они обязательно должны пересекаться.

17. Какие точки называются конкурирующими?

Конкурирующие точки используются для определения видимости геометрических фигур на плоскости проекций. Где видимые объекты отображают сплошной основной линией, не видимые - тонкой пунктирной линией.

Конкурирующие точки - это точки, расположенные на одном проецирующем луче

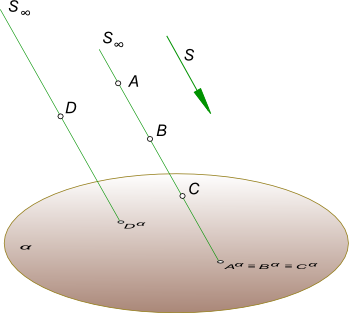
Конкурирующие точки

Определение видимости в системе параллельного проецирования изображенной на рисунке, затруднительно так как по одной проекции нельзя выделить наиболее удаленную от проекции точку. Образно говоря, конкурирующие точки - это как две лошади на скачках: когда на тебя скачут, вроде вместе, а как сбоку посмотришь - сразу видно, кто впереди, а кто сзади.
Однако на эпюре Монжа в ортогональной системе плоскостей проекций данная задача легко решается.

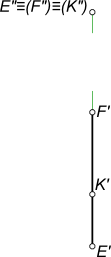
Конкурирующие точки

Применительно к нашему чертежу конкурирующими будут точки: E,K и F принадлежащие фронтально проецирующей прямой. Видимой на фронтальной плоскости проекций будет точка наиболее удаленная от нее - это точка E. ЕЕ горизонтальная проекция E` наиболее удалена от оси x.
Конкурирующие точки обозначают на эпюре с помощью знака ≡, означающего совпадение указанных проекций, при этом проекции невидимых точек берут в круглые скобки.

18. На основании теоремы прямого угла сформируйте графический признак изображения прямого угла на эпюре?