Если точка принадлежит прямой, то её проекции принадлежат одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 8 точек, только одна точка С лежит на прямой АВ, так как отвечает требованиям аксиомы.
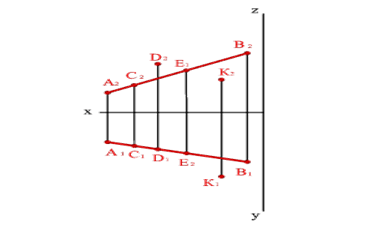
Рисунок 8. Взаимное расположение точки и прямой 
22. Какая прямая называется прямой общего положения?
По расположению относительно плоскостей проекций бывает прямая общего положения и частного.
Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Отрезок [AB] определяющий прямую l занимает произвольное положение по отношению к плоскостям проекций (углы наклона прямой l к плоскостям H, V, и W произвольные - отличные от 0 и 90 град.). Такая прямая есть прямая общего положения.
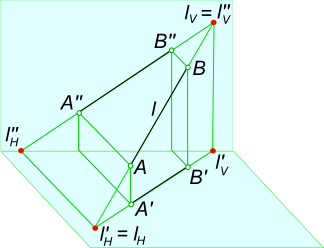
Прямая общего положения
Прямая общего положения пересекает все три плоскости проекций. Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой.

Прямая общего положения
В зависимости от того, с какой плоскостью проекции происходит встреча прямой l, следы обозначают и называют:
l H - горизонтальный след прямой l;
l V - фронтальный след прямой l;
l W - профильный след прямой l.
По расположению относительно плоскостей проекций бывают прямые частного положения:
Горизонтальная прямая;
Фронтальная прямая;
Профильная прямая;
Проецирующие прямые.
23. Какие частные положения прямых Вы знаете?
Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо плоскости проекций. Существуют 6 прямых частного положения, которые, в свою очередь, делятся на две группы:
1. Прямые уровня – это прямые, параллельные только одной плоскости проекций:
а) горизонталь (h) – прямая, параллельная горизонтальной плоскости проекций .
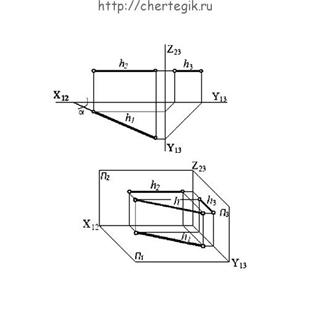
α – угол, образованный горизонталью с фронтальной плоскостью
б) фронталь (f)- прямая, параллельная фронтальной плоскости проекций .
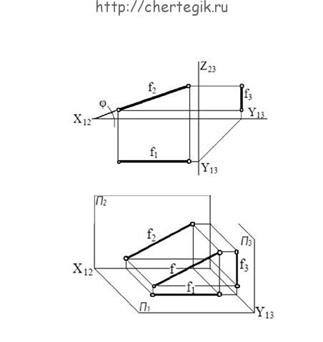
φ — угол, образованный фронталью с горизонтальной плоскостью
проекций.
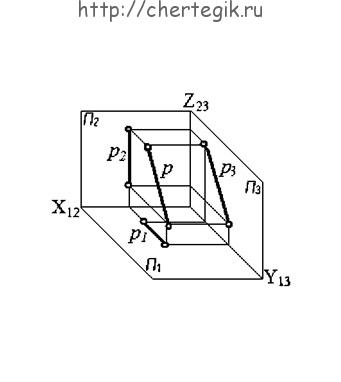
в) профильная прямая (p) — прямая, параллельная профильной плоскости проекций.
2. Проецирующие прямые – это прямые, перпендикулярные какой-либо плоскости проекций:
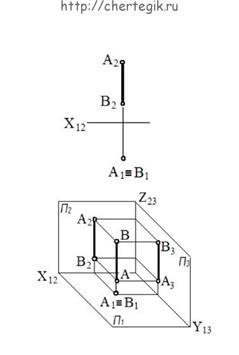
а) горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций.
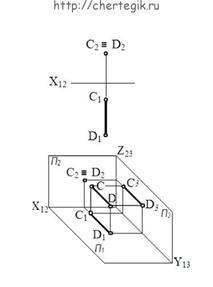
б) фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций.
в) профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций. 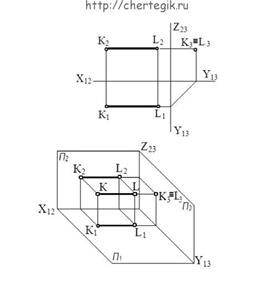
При сравнительном анализе изображений прямых частного следует:
1. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции обязательно параллельны осям проекций.
2. Проекция прямой уровня, к той плоскости, которой она параллельна, составляет с осями проекций углы, равные углам наклона линии уровня с плоскостями проекций.
3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость является точка, а вторая проекция располагается перпендикулярно осям проекций.
24. Как определить на эпюре принадлежность точки к прямой линии?
Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.

Принадлежность точки прямой
В символической форме эти выражения могут быть записаны
B ∈ a ⇒ B` ∈ a` ∧ B" ∈ a"
Задача на принадлежность точки прямой может быть выражена следующим образом:
- заключить точку B(B`, B") в;
- провести через точку B(B`, B")
прямую a общего положения.
На эпюре решение данной задачи сводится к проведению через проекции заданной точки одноименных проекций прямой.
Положение в пространстве прямой линии однозначно определяется заданием двух ее точек (рис. 29, а).
Эпюр прямой также может быть представлен в виде эпюра двух точек прямой. На рис. 29, б прямая а задана двумя точками А и В: а = {А; В). Эпюры этих точек определяют эпюр прямой: ai={Ai; Bi) и аг = {Аг Вг}-
Кроме того, комплексный чертеж прямой может быть представлен двумя проекциями прямой: a={ai; аг} (рис. 29, в).
Во всех этих случаях при реконструкции в пространстве прямая а определяется однозначно, так как плоскости Т и Г, проецирующие прямую на Пг и Пь пересекутся по единственной прямой а (плоскость Т проходит через прямую аг перпендикулярно к Пг; плоскость Г проходит через прямую ai перпендикулярно к Пг).
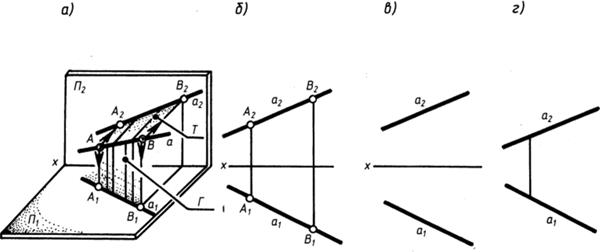
Рис. 29
На безосном эпюре (рис. 29, г) для задания прямой а достаточно изобразить ее проекции ai, аг и линию проекционной связи.
Прямая аг есть фронтальная проекция прямой а на плоскость проекций Пг (а с Т; Т 1 Пг; аг = Тп Пг).
Прямая ai есть горизонтальная проекция прямой а на плоскость проекций Щ (а с Г; Г1 Щ; ai = Г п Ш).
Прямая аз есть профильная проекция прямой а на плоскость проекций Пз (строится как линия пересечения профильной плоскости проекций Пз с проецирующей плоскостью, проходящей через прямую а перпендикулярно к Пз).
Если точка принадлежит прямой, то ее проекции расположатся на одноименных проекциях прямой (см. рис. 29, а, б). Например, А с а =>А2 са2; А1са1; AXAZ ± х.
25. Какими методами на эпюре определяется натуральная длина отрезка прямой линии общего положения и углы ее наклона к плоскостям проекций?
Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника. В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
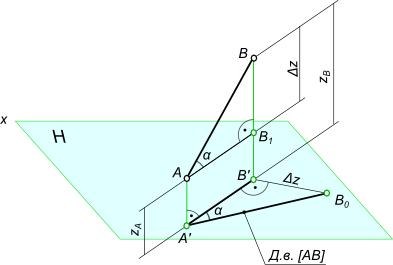
Углы наклона прямой
| 1. | tg α= BB1/AB1=(BB`−B`B1)/AB1=(zB−zA)/A`B` |
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).
Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
- первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
- из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
- гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
- угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.
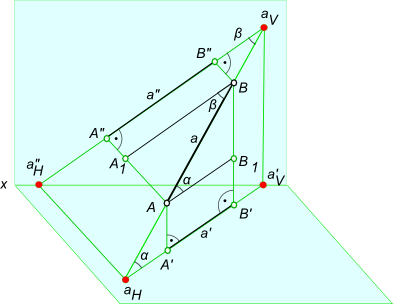
Углы наклона прямой
Для графического определения на эпюре Монжа действительной величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции.
| 2. | tg α= BB1/AB1=(BB`−B`B1)/AB1=(zB−zA)/A`B` |
| 3. | tg β= AA1/BA1=(AA"−A"A1)/BA1=(yA−yB)/A"B" |
Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников ΔA`B`B0 или ΔA"B"A0 и попутно углов его наклона:
- α к горизонтальной плоскости проекции;
- β к фронтальной плоскости проекции.
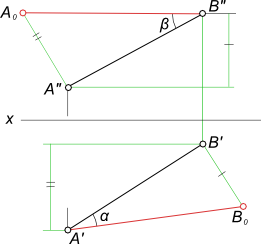
Углы наклона прямой
Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
- Горизонтальная прямая;
- Фронтальная прямая;
- Профильная прямая
26. Как узнать по проекциям двух прямых линий об их взаимном расположении в пространстве?
Прямые линии в пространстве могут занимать различные положения по отношению друг к другу. Они могут:
а) пересекаться; б) скрещиваться; в) быть взаимнопараллельными.
Чтобы по чертежу определить взаимное положение прямых, установим признаки пересечения, скрещивания и параллельности их на комплексном чертеже.
Пусть имеются прямая, проходящая через точки А и В, и некоторая точка С. Возможны два случая взаимного расположения прямой ЛВ и точки С: либо точка С принадлежит этой прямой, либо не принадлежит. Если точка принадлежит прямой, то ее проекции будут принадлежать одноименным проекциям прямой. Если точка Сне принадлежит прямой АВ, то проекция точки С может принадлежать проекции прямой, а может и не принадлежать ей. Возьмем, например, горизонтальную плоскость проекций (рис. 2.5). Если перпендикуляр, опущенный из точки Сна эту плоскость проекций, пересекает прямую АВ, то горизонтальная проекция точки С (т. С,) будет лежать на горизонтальной проекции прямой АВ (рис. 2.5, а). Если опущенный из точки С перпендикуляр не пересекает прямую АВ, то горизонтальная проекция точки С (т. С{) не будет принадлежать горизонтальной проекции прямой (рис. 2.5, б). Для остальных плоскостей проекций положение аналогичное.
Заметим, что в черчении прямая линия может обозначаться по определяющим ее точкам (например, прямая АВ — это прямая, проходящая через точки А и В) или строчными буквами латинского алфавита а, Ь, с,...
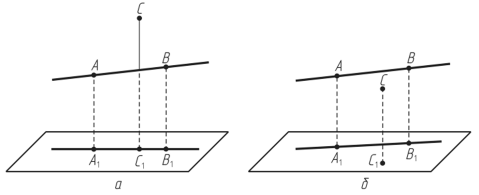
Рис. 2.5
Дата: 2019-03-05, просмотров: 480.