При решении дифференциальных уравнений операторным методом, после того, как будет найдено изображение решения, иногда следует по изображению найти оригинал.

В общем случае эта задача решается с помощью преобразования, обратного преобразованию Лапласа-Карсона.

В более простых случаях, если изображение есть правильная рациональная дробь, то, разложив её на элементарные дроби, оригинал можно найти, используя полученную таблицу.

Известно, что элементарными дробями I рода называются дроби вида 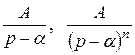, а элементарными дробями II рода называются дроби вида  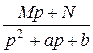и .

Как найти для них оригиналы?

1. Для дроби 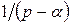 оригинал найдем, используя правило интегрирования оригинала .

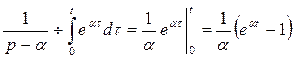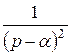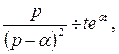2. Для получения оригинала функции  воспользуемся изображением функции  и правилом интегрирования оригинала. Так как то .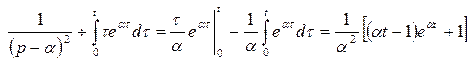

Аналогично можно найти оригиналы для функци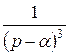й  и .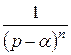

3. Как найти оригинал для функции ?

Корни знаменателя комплексные. Выделяя в знаменателе полный квадрат, можно его привести к виду 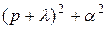 или 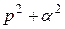. Оригинал для функции  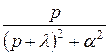можно найти, используя формулу 11 из таблицы 1, а для функции  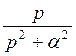- по формуле 6. Оригинал для функции  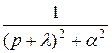можно найти, используя правило интегрирования оригинала. Так как

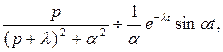 то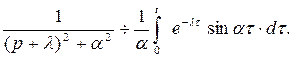

    Вычислим определенный интеграл, используя формулу интегрирования по частям:

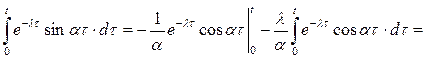
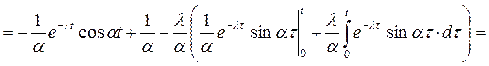
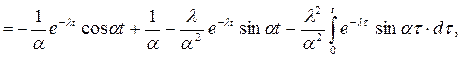 тогда

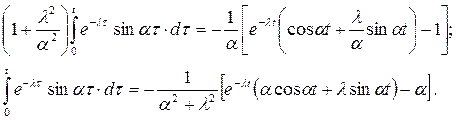
Таким образом: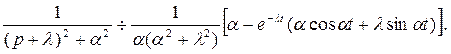

4. Найдём оригинал для элементарной дроби второго рода .

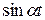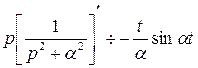Воспользуемся изображением  и правилом дифференцирования изображения. Так как  то , или

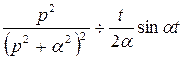.                                          (2.4)

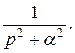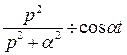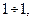Найдем оригинал для функции  Так как  и  то 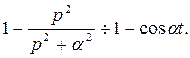 Таким образом: .         (2.5)

Из соотношений (2.4) и (2.5) и свойства линейности оператора Лапласа-Карсона получим:

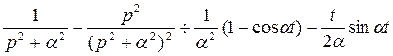, или

.

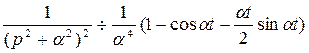Аналогичными преобразованиями можно получить оригиналы для других элементарных дробей II рода.

Операционный метод решения некоторых дифференциальных

  уравнений

Линейные дифференциальные уравнения с постоянными

Коэффициентами

    Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка с постоянными коэффициентами.

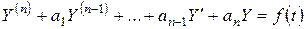.                 (2.6)

    Найдем его частное решение 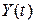 при 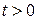, удовлетворяющее начальным условиям:

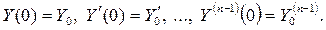                  (2.7)

Применим к соотношению (2.6) оператор Лапласа-Карсона, т.е. умножим все члены равенства на 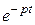 и проинтегрируем в пределах от 0 до 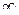, затем результат умножим на p.

Обозначим . Изображение производных найдем на основании правил дифференцирования и интегрирования оригинала. Изображение функции найдем по таблице 1 (см. с. 48). Таким образом, используя условия (2.7), получим: ; ;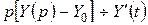

; …; .

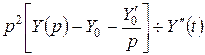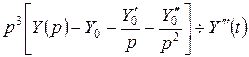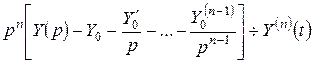Запишем уравнение (2.6) в операторной форме.

.

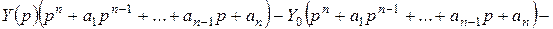
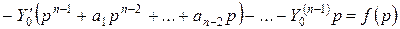Обозначим через 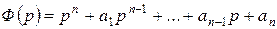 и

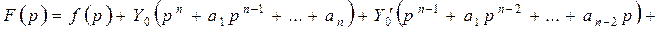
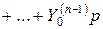. Тогда . Это есть изображение искомого частного решения. Оригинал находим или по таблице 1 или по формуле обращения, которая будет получена ниже.

Если 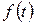 является линейной комбинацией функций вида 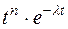, то ее изображение есть рациональная дробь, показатель степени числителя которой не превышает показателя степени знаменателя. Такого же типа будет дробь . Выделив целую часть и разложив оставшуюся элементарную дробь на простейшие, найдем оригинал 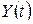 по таблице 1.

Решение дифференциального уравнения свелось к решению алгебраического уравнения, линейного относительно неизвестной функции 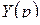, и нахождению по изображению оригинала.

Пример 1. Постоянное напряжение, равное 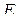, включено в цепь с последовательно включенным постоянным сопротивлением  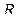и самоиндукцией 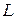. Определить ток  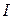в цепи как функцию времени при > 0, если 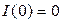 (см. рис. 2.1).

При последовательном соединении элементов падение напряжения в цепи складывается из падений напряжения на отдельных участках цепи. Поэтому

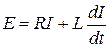                                (2.8)

Обозначим 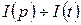, тогда  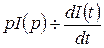и 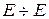. В операторной форме дифференциальное уравнение (2.8) примет вид:

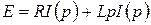, тогда .

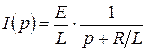По формуле 3 таблицы 1 найдем .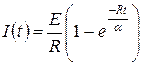

Пример 2

Дано ; ; .

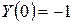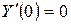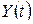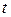Найти  при  > 0. Пусть  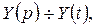тогда  и 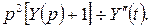 Применяя формулу 13 из таблицы 1, получим:

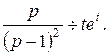
Запишем дифференциальное уравнение в операторной форме:

, или .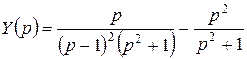

Разложив дробь на элементарные дроби, получим:

 Тогда .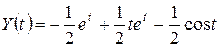

Пример 3

.

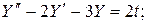
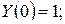
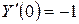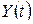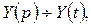Найти  при  > 0. Пусть  тогда

.

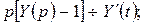
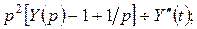
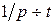В операторной форме уравнение примет вид:

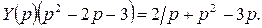 Отсюда

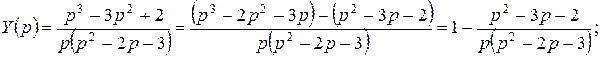
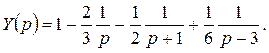 Тогда

.