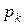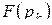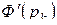ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
Рубцовский индустриальный институт
ГОУ ВПО «Алтайский государственный технический университет
Им. И.И. Ползунова»
И.И. Кулешова
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭНЕРГЕТИКЕ
Методическое пособие
Часть 1
Рубцовск 2007
УДК 510.6
510.22
517.445
Кулешова И.И. Математические методы в энергетике: Методическое пособие / Рубцовский индустриальный институт. – Рубцовск, 2007. Часть 1 - 63 с.
Данное учебно-методическое пособие предназначено для студентов дневной и заочной форм обучения электротехнического факультета, изучающих курс по выбору «Математические задачи энергетики».
В работе кратко изложен материал по математической логике и операционному исчислению, приведены примеры решения задач по данным темам, предложены варианты заданий для текущего контроля.
Рассмотрено и одобрено на заседании НМС Рубцоского индустриального института.
Протокол № 4 от 05.06.07.
Рецензент: к.ф.-м.н., профессор Н.А. Кулагина
© Рубцовский индустриальный институт, 2007
Содержание
| ВВЕДЕНИЕ | 4 |
| ГЛАВА 1. ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ | 5 |
| 1.1. Понятие высказывания | 5 |
| 1.2. Логические операции над высказываниями | 6 |
| 1.3. Формулы алгебры логики | 10 |
| 1.4. Равносильные формулы алгебры логики | 11 |
| 1.5. Равносильные преобразования формул | 16 |
| 1.6. Приложения алгебры логики высказываний к релейно-контактным схемам (РКС) | 17 |
| ГЛАВА 2. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ | 19 |
| 2.1. Линейные операторы и действия над ними | 19 |
| 2.2. Преобразование Лапласа и его свойства | 21 |
| 2.3. Правила операционного исчисления | 24 |
| 2.4. Преобразование некоторых употребительных функций | 29 |
| 2.5. Операционный метод решения некоторых дифференциальных уравнений | 34 |
| 2.6. Формула Хевисайда (вторая теорема разложения) | 41 |
| Контролирующие материалы по дисциплине «Математические задачи энергетики» (дневная форма обучения) | 50 |
| Контролирующие материалы по дисциплине «Математические задачи энергетики» (заочная форма обучения) | 58 |
ВВЕДЕНИЕ
Содержание настоящего курса составляет лишь часть обширной теории математических методов в энергетике. В данном курсе рассматриваются элементы алгебры логики с приложениями в электротехнике и методы операционного исчисления.
Аппарат математической логики в настоящее время нашел широкое применение в медицине, лингвистике, педагогике, психологии, экономике, технике. Цель данной работы – показать применение формул алгебры логики к описанию релейно-контактных схем и упрощению их.
Под операционным исчислением понимается совокупность методов прикладного анализа, позволяющих наиболее простыми и экономными средствами получать решения линейных дифференциальных уравнений (обыкновенных и с частными производными), разностных и некоторых видов интегральных и интегро-дифференциальных уравнений.
К уравнениям таких видов приводят задачи из различных разделов электротехники. Построение операционного исчисления базируется на идее функционального преобразования.
Преобразование обладает такими свойствами, что операциям анализа – дифференцированию и интегрированию над оригиналами – соответствуют операции алгебры – умножение и деление над изображениями. Путем такого преобразования дифференциальные и интегральные уравнения заменяются алгебраическими уравнениями.
ГЛАВА 1. ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ
Понятие высказывания
Основным (неопределяемым) понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».
Приведем примеры высказываний.
1) Новгород стоит на Волхове.
2) Париж - столица Англии.
3) Карась не рыба.
4) Число 6 делится на 2 и на 3.
5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.
Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны.
Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием.
Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если ..., то ...», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась - рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если ..., то ...». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: х, у, z , .... а, в, с , ...; истинное значение высказывания - буквой «и» или цифрой 1, а ложное значение - буквой «л» или цифрой 0.
Если высказывание а истинно, то будем писать а=1, если а ложно, то а=0.
Формулы алгебры логики
С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками. Например, из трех высказываний х, у, z можно построить высказывания: ( x & y ) 
 и х
и х 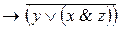 .
.
Первое из них есть дизъюнкция конъюнкции х, у и отрицания выказывания z, а второе высказывание есть импликация, посылкой которой является высказывание х, а заключением - отрицание дизъюнкции высказывания у и конъюнкции высказываний х, z .
Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, называется формулой алгебры логики.
Формулы алгебры логики будем обозначать большими буквами латинского алфавита А, В, С, ...
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
В связи с этим формулы:
(х&у) 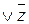 и х
и х 
могут быть записаны так:
 и
и  .
.
Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в нее элементарных высказываний. Например, логическим значением формулы  в случае, если х = 1, у = 1, z = 0, будет истина, то есть
в случае, если х = 1, у = 1, z = 0, будет истина, то есть  =1.
=1.
Все возможные логические значения формулы, в зависимости от значений входящих в нее элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности.
Например, для формулы 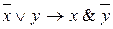 таблица истинности имеет вид:
таблица истинности имеет вид:
| х | у | 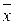
| 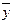
| 
| х& 
| 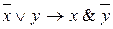
|
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
Легко видеть, что если формула содержит п элементарных высказываний, то она принимает 2n значений, состоящих из нулей и единиц, или, что то же, таблица содержит 2n строк.
Примеры операторов
Пример 1. Пусть М – множество функций, дифференцируемых n раз.
Нахождение первой производной – оператор над множеством функций М, обозначают его D или 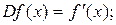
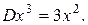
Нахождение второй производной – также оператор, обозначают его 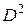 или
или 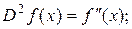

Нахождение n-й производной – оператор, обозначают его 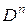 или
или
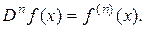
Пример 2. Однократное, двукратное, n-кратное интегрирование – операторы, для которых употребляются символы 
 …
…  или
или
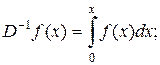

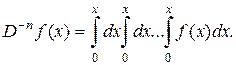
Пример 3. Пусть 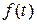 – функция вещественного аргумента
– функция вещественного аргумента 
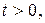
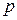 – комплексное число;
– комплексное число; 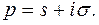 Если сходится
Если сходится 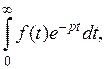 то он является некоторой функцией аргумента p:
то он является некоторой функцией аргумента p: 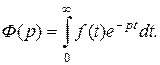
Интеграл, стоящий справа, называется интегралом Лапласа. Преобразование, по которому функции 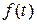 ставится в соответствие функция
ставится в соответствие функция  , называется преобразованием или интегральным оператором Лапласа.
, называется преобразованием или интегральным оператором Лапласа.
Пример 4. Пусть  дважды дифференцируемая функция и
дважды дифференцируемая функция и
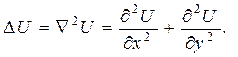
Преобразование, по которому функции U ставится в соответствие функция 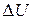 , называется дифференциальным оператором Лапласа.
, называется дифференциальным оператором Лапласа.
Действия над операторами
Над операторами можно производить арифметические операции.
Сумма двух операторов K 1 и K 2 определяется соотношением

Произведение операторов K 1 и K 2 определяется соотношением
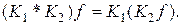
Если K 1 и K 2 равные операторы, 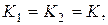 то их произведение обозначают K 2.
то их произведение обозначают K 2.
Оператор, от применения которого функция не изменяется, называется единичным, обозначается символом E: 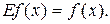
Два оператора называются взаимно обратными, если их произведения дают единичный оператор, т.е. если 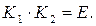 Для взаимно обратных операторов приняты обозначения
Для взаимно обратных операторов приняты обозначения 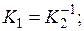
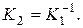
Определение 2.2 . Оператор K называется линейным, если он обладает двумя свойствами:
1) аддитивности:  ;
;
2) однородности: 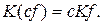
Все указанные в примерах операторы являются линейными.
2.2. Преобразование Лапласа и его свойства
Теорема 2.1
Если можно подобрать два такие положительные числа 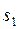 и M, что для любого
и M, что для любого 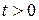
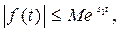 т.е. если
т.е. если  растет медленнее, чем некоторая экспоненциальная функция, то функция
растет медленнее, чем некоторая экспоненциальная функция, то функция  имеет ограниченный рост с показателем роста, меньшим
имеет ограниченный рост с показателем роста, меньшим 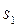 .
.
Доказательство

если 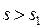 .
.
Итак, 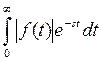 сходится при всех
сходится при всех 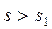 , следовательно,
, следовательно,  имеет ограниченный рост с показателем s0, s0 < s1.
имеет ограниченный рост с показателем s0, s0 < s1.
К функциям с ограниченным ростом относятся: 
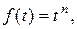
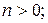
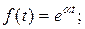
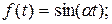
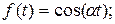

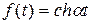 .
.
Примерами функций с неограниченным ростом являются:

Теорема 2.2
Если 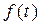 – функция с ограниченным ростом, то при всех p таких, что
– функция с ограниченным ростом, то при всех p таких, что  где
где 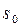 – показатель роста
– показатель роста  , интеграл Лапласа сходится.
, интеграл Лапласа сходится.
Доказательство
Обозначим 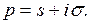 Тогда
Тогда

Этот интеграл по условию теоремы сходится при всех 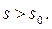 Следовательно, и первый интеграл при всех p, для которых
Следовательно, и первый интеграл при всех p, для которых 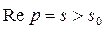 , также сходится.
, также сходится.
Во всех дальнейших рассуждениях, если не оговорено обратное, будем предполагать, что оригинал  имеет ограниченный рост.
имеет ограниченный рост.
Сложение
Так как преобразование Лапласа-Карсона – операция линейная, то очевидно, что из

следует
 .
.
Изображение суммы равно сумме изображений. Оригинал суммы равен сумме оригиналов.
Изображение постоянной
Изображение постоянной равно ей самой. Действительно, 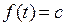 ;
; 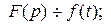
 при
при 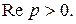
Дифференцирование оригинала
Пусть  Каково изображение
Каково изображение  ?
?
Обозначим 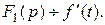 Тогда
Тогда
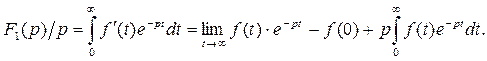
Если  – функция с ограниченным ростом, то
– функция с ограниченным ростом, то 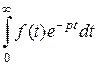 сходится при всех p,
сходится при всех p,  , где
, где 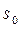 – показатель роста
– показатель роста 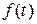 . Но это возможно, только если
. Но это возможно, только если 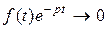 при
при 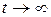 , а тогда
, а тогда 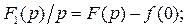

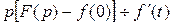 , где
, где 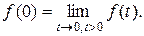
Если  то
то  Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Пусть  . Найдем изображение функции
. Найдем изображение функции 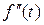 , воспользовавшись свойством дифференцирования оригинала.
, воспользовавшись свойством дифференцирования оригинала.
Обозначим 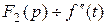 . Тогда
. Тогда
 , или
, или 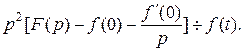
Если при 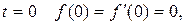 то
то 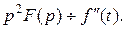
Аналогично можно найти изображение производной любого порядка.
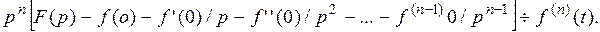
Если при 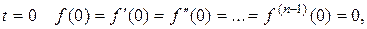 то
то 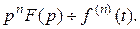
Следовательно, если функция  удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на
удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на  .
.
Интегрирование оригинала
Пусть 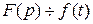 . Каково изображение
. Каково изображение 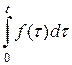 ? Обозначим его через
? Обозначим его через  т.е.
т.е. 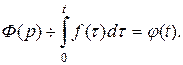 Продифференцируем
Продифференцируем 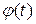 .
.
Пусть 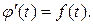 Но
Но  , поэтому
, поэтому 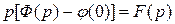 . Остаётся
. Остаётся 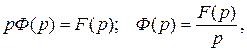 при
при 
Итак, 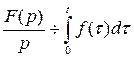 , т.е. при интегрировании оригинала от нуля до t изображение делится на p.
, т.е. при интегрировании оригинала от нуля до t изображение делится на p.
Найдем изображение для неопределенного интеграла (первообразной) 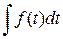 =
= 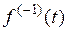 . Определенный интеграл
. Определенный интеграл 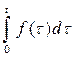 также является первообразной для функции
также является первообразной для функции  , поэтому
, поэтому  . Положив
. Положив 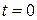 , получим
, получим 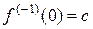 .
.
Тогда  , где
, где 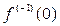 – постоянная.
– постоянная.
Изображение функции 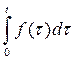 найдено ранее, поэтому
найдено ранее, поэтому
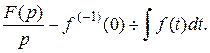
Теорема 2.3
Если  – функция с ограниченным ростом,
– функция с ограниченным ростом,  , то
, то  при
при  .
.
Доказательство
Пусть  , тогда
, тогда  .
.
Рассмотрим сколь угодно малое 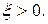 Покажем, что можно указать такое p, с достаточно большой вещественной частью
Покажем, что можно указать такое p, с достаточно большой вещественной частью 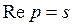 , для которого
, для которого
 В равенстве для
В равенстве для 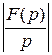 разобьём интеграл, стоящий справа, на два интеграла:
разобьём интеграл, стоящий справа, на два интеграла:
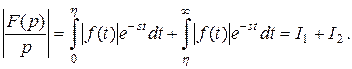
Рассмотрим 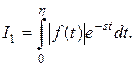 Так как
Так как 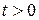 , то для тех p, для которых
, то для тех p, для которых 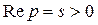 ,
, 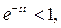 следовательно,
следовательно, 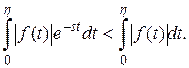 Подберём
Подберём 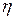 так, чтобы интеграл
так, чтобы интеграл 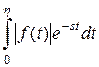 был меньше
был меньше 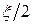 . Это возможно, потому что функция
. Это возможно, потому что функция 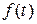 непрерывна или кусочно-непрерывна при
непрерывна или кусочно-непрерывна при 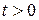 и
и 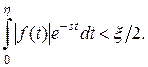
Рассмотрим 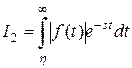 , где
, где  – функция с ограниченным ростом,
– функция с ограниченным ростом, 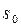 – показатель роста. Рассмотрим
– показатель роста. Рассмотрим 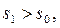
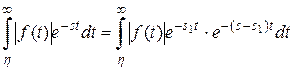 . Функция
. Функция  при
при  , наибольшее значение на промежутке
, наибольшее значение на промежутке 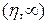 имеет при
имеет при  . Интеграл
. Интеграл 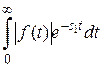 сходится, т.к.
сходится, т.к.  – функция с ограниченным ростом, а
– функция с ограниченным ростом, а 
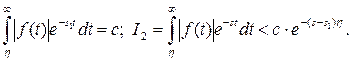
Здесь c, s1 и 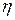 -фиксированные величины, а переменная s произвольная. Взяв
-фиксированные величины, а переменная s произвольная. Взяв 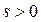 и достаточно большим, получим:
и достаточно большим, получим: 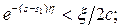
 т.к.
т.к.  - убывающая функция аргумента s.
- убывающая функция аргумента s.
Итак, при достаточно больших 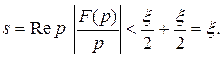 Рассуждения справедливы для любых
Рассуждения справедливы для любых 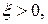 сколь угодно малых. Следовательно, выполняется неравенство:
сколь угодно малых. Следовательно, выполняется неравенство:  при
при 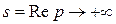 .
.
Теорема смещения
Теорема 2.4 (смещения)
Если  , то
, то 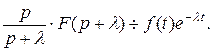
Доказательство
Пусть  . Найдем изображение функции
. Найдем изображение функции 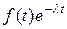 .
.
Обозначим 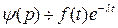 , тогда
, тогда
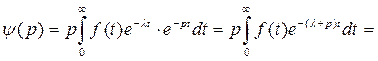

Отсюда 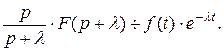 Предполагается, что
Предполагается, что 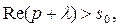 т.е.
т.е.
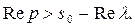
Название теоремы объясняется её геометрической интерпретацией.
Если p – вещественная переменная, то при умножении оригинала на  график изображения смещается на -
график изображения смещается на - 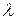 по оси p. Ординаты графика при
по оси p. Ординаты графика при
этом умножаются на 
2.4. Преобразование некоторых употребительных функций
Коэффициентами
Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка с постоянными коэффициентами.
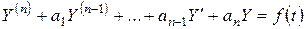 . (2.6)
. (2.6)
Найдем его частное решение 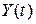 при
при  , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:
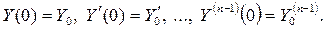 (2.7)
(2.7)
Применим к соотношению (2.6) оператор Лапласа-Карсона, т.е. умножим все члены равенства на 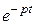 и проинтегрируем в пределах от 0 до
и проинтегрируем в пределах от 0 до 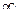 , затем результат умножим на p.
, затем результат умножим на p.
Обозначим  . Изображение производных найдем на основании правил дифференцирования и интегрирования оригинала. Изображение функции найдем по таблице 1 (см. с. 48). Таким образом, используя условия (2.7), получим:
. Изображение производных найдем на основании правил дифференцирования и интегрирования оригинала. Изображение функции найдем по таблице 1 (см. с. 48). Таким образом, используя условия (2.7), получим:  ;
; 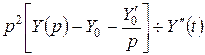 ;
;
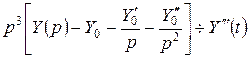 ; …;
; …; 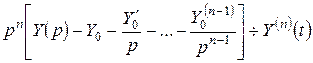 .
.
Запишем уравнение (2.6) в операторной форме.
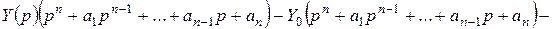
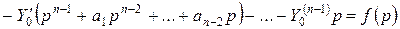 .
.
Обозначим через 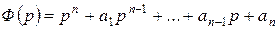 и
и
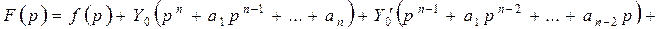
 . Тогда
. Тогда  . Это есть изображение искомого частного решения. Оригинал находим или по таблице 1 или по формуле обращения, которая будет получена ниже.
. Это есть изображение искомого частного решения. Оригинал находим или по таблице 1 или по формуле обращения, которая будет получена ниже.
Если 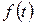 является линейной комбинацией функций вида
является линейной комбинацией функций вида 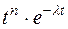 , то ее изображение есть рациональная дробь, показатель степени числителя которой не превышает показателя степени знаменателя. Такого же типа будет дробь
, то ее изображение есть рациональная дробь, показатель степени числителя которой не превышает показателя степени знаменателя. Такого же типа будет дробь  . Выделив целую часть и разложив оставшуюся элементарную дробь на простейшие, найдем оригинал
. Выделив целую часть и разложив оставшуюся элементарную дробь на простейшие, найдем оригинал  по таблице 1.
по таблице 1.
Решение дифференциального уравнения свелось к решению алгебраического уравнения, линейного относительно неизвестной функции 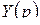 , и нахождению по изображению оригинала.
, и нахождению по изображению оригинала.
Пример 1. Постоянное напряжение, равное 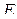 , включено в цепь с последовательно включенным постоянным сопротивлением
, включено в цепь с последовательно включенным постоянным сопротивлением 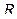 и самоиндукцией
и самоиндукцией 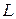 . Определить ток
. Определить ток 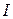 в цепи как функцию времени при
в цепи как функцию времени при  > 0, если
> 0, если 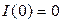 (см. рис. 2.1).
(см. рис. 2.1).

При последовательном соединении элементов падение напряжения в цепи складывается из падений напряжения на отдельных участках цепи. Поэтому
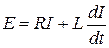 (2.8)
(2.8)
Обозначим 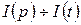 , тогда
, тогда 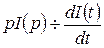 и
и  . В операторной форме дифференциальное уравнение (2.8) примет вид:
. В операторной форме дифференциальное уравнение (2.8) примет вид:
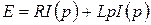 , тогда
, тогда 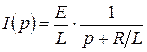 .
.
По формуле 3 таблицы 1 найдем 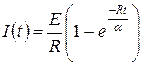 .
.
Пример 2
Дано  ;
; 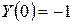 ;
; 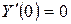 .
.
Найти 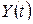 при
при  > 0. Пусть
> 0. Пусть 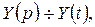 тогда
тогда  и
и 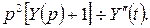 Применяя формулу 13 из таблицы 1, получим:
Применяя формулу 13 из таблицы 1, получим:
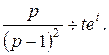
Запишем дифференциальное уравнение в операторной форме:
 , или
, или 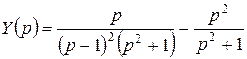 .
.
Разложив дробь на элементарные дроби, получим:
 Тогда
Тогда 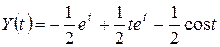 .
.
Пример 3
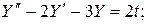
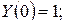
 .
.
Найти 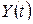 при
при  > 0. Пусть
> 0. Пусть 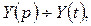 тогда
тогда
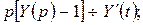
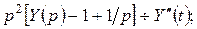
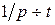 .
.
В операторной форме уравнение примет вид:
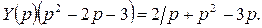 Отсюда
Отсюда
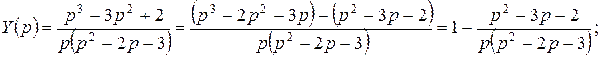
 Тогда
Тогда
 .
.
Вывод формулы Хевисайда
Если изображение есть дробно-рациональная функция, удовлетворяющая некоторым условиям, то нахождение оригинала можно упростить, воспользовавшись формулой Хевисайда.
Пусть  есть рациональная дробь.
есть рациональная дробь.
Формулу выведем при некоторых ограничениях:
1. Если показатель степени многочлена 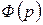 есть n, то показатель степени
есть n, то показатель степени  не больше n.
не больше n.
2. Все корни многочлена 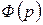 – простые.
– простые.
3. Среди корней многочлена 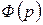 нет нуля.
нет нуля.
4. Числитель и знаменатель не имеют общих множителей, в противном случае их надо на этот множитель сократить (корни знаменателя не являются корнями числителя).
Замечание 1. Если 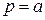 является корнем кратности k многочлена
является корнем кратности k многочлена 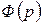 , то для многочлена
, то для многочлена 
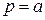 – корень кратности
– корень кратности 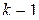 .
.
Пусть 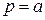 – корень кратности
– корень кратности 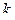 для многочлена
для многочлена 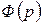 , тогда
, тогда 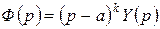 , где
, где 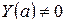 . Найдем производную от
. Найдем производную от 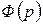 по переменной p:
по переменной p:
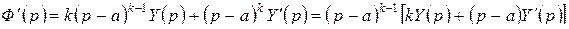 .
.
Выражение, стоящие в квадратных скобках, при  в нуль не обращается, потому для многочлена
в нуль не обращается, потому для многочлена 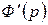
 является корнем кратности
является корнем кратности 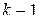 . Если
. Если 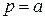 - простой корень многочлена
- простой корень многочлена 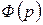 , то для
, то для 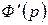
 корнем не является.
корнем не является.
Вывод формулы Хевисайда.
Пусть 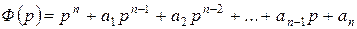 ; где
; где 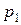 ,
,  , …,
, …, 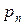 - корни
- корни 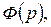 тогда
тогда  ···
··· 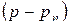 .
.
Показатель степени числителя дроби 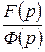 не превышает показателя степени знаменателя. Разделим
не превышает показателя степени знаменателя. Разделим  на p, чтобы гарантировать правильность дроби, и разложим получившуюся дробь на элементарные:
на p, чтобы гарантировать правильность дроби, и разложим получившуюся дробь на элементарные:
 . (2.11)
. (2.11)
Определим коэффициенты 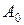 ,
, 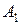 , …,
, …,  . Для этого умножим левую и правую части равенства (2.11) на p и, положив
. Для этого умножим левую и правую части равенства (2.11) на p и, положив 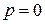 , найдем
, найдем 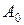 ;
; 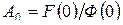 .
.
Умножив левую и правую части равенства (2.11) на 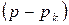 и положив
и положив  , найдем
, найдем 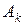 .
.

 где
где 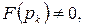
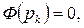
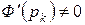 .
.
Тогда изображение есть  ,
,
соответственно, оригинал 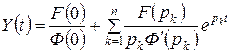 .
.
Пример 1.  Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: при
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: при 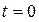
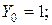
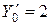 .
.
Запишем уравнение в операторной форме:
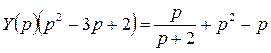 , или
, или 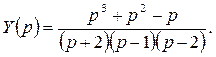
Применим формулу Хевисайда к функции 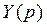 , где
, где  ,
,
|
 . Найдем
. Найдем 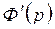 .
.
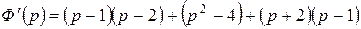 .
.
При этом 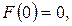
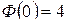 . Тогда оригинал
. Тогда оригинал
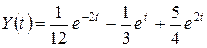 .
.
Замечание 2. Если корни знаменателя  простые, но среди них есть нулевой корень, то оригинал можно получить, применяя к дроби
простые, но среди них есть нулевой корень, то оригинал можно получить, применяя к дроби 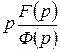 формулу Хевисайда и свойство об интегрировании оригинала.
формулу Хевисайда и свойство об интегрировании оригинала.
Пример 2. Найти частное решение дифференциального уравнения 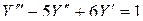 , удовлетворяющее начальным условиям: при
, удовлетворяющее начальным условиям: при 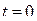
 . Запишем уравнение в операторной форме:
. Запишем уравнение в операторной форме:
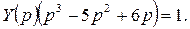 Отсюда
Отсюда 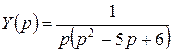 .
.
|
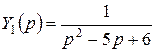 , где
, где
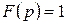 и
и 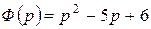 ,
,  .
.
Найдем 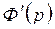 .
.
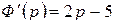 ,
,  .
.
Тогда  следовательно,
следовательно, 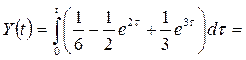
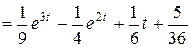 .
.
Замечание 3. В том случае, если среди корней 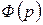 есть кратные, тоже можно составить формулу разложения. Но нахождение коэффициентов этой формулы сильно усложняется.
есть кратные, тоже можно составить формулу разложения. Но нахождение коэффициентов этой формулы сильно усложняется.
Рассмотрим пример на применение формулы Хевисайда, если многочлен 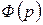 имеет мнимые корни.
имеет мнимые корни.
Пример 3. 
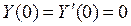 .
.
Запишем уравнение в операторной форме:
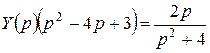 . Отсюда
. Отсюда 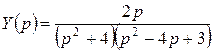 , где
, где 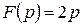 и
и  . При этом
. При этом 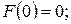
 . Найдем
. Найдем  .
.
|
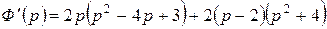 .
.
Тогда  ,
,
или 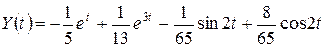 .
.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
Рубцовский индустриальный институт
ГОУ ВПО «Алтайский государственный технический университет
Им. И.И. Ползунова»
И.И. Кулешова
Дата: 2019-02-19, просмотров: 301.