к релейно-контактным схемам (РКС)

Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:

1) переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;

2) соединяющие их проводники;

3) входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В. Переключателю Р поставим в соответствие высказывание р, гласящее: «Переключатель Р замкнут». Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения, т.е. схема пропускает ток. Если р ложно, то переключатель разомкнут и схема тока не проводит. Таким образом, если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответствие переключательная схема с двумя полюсами (двухполюсная схема).

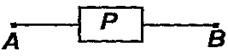
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

Так, конъюнкции двух высказываний р& q ставится в соответствие схема

а дизъюнкции р vq – схема:

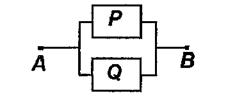
Каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики. Поэтому возможности схемы можно выявить, изучая соответствующую ей формулу, а упрощение схемы можно свести к упрощению формулы.

Пример 1. Составить РКС для формулы .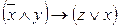

Решение. Упростим данную формулу с помощью равносильных преобразований:

.

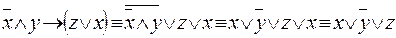Тогда РКС для данной формулы имеет вид:

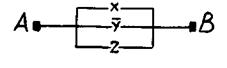
Пример 2. Упростить РКС:

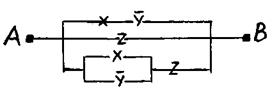
Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:

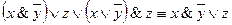
(к последним двум слагаемым применили закон поглощения).

Тогда упрощенная схема выглядит так:

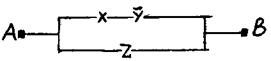
ГЛАВА 2. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

Линейные операторы и действия над ними

Пусть имеются два множества функций M и N.

Определение 2.1. Оператором над множеством функций M называется такое преобразование, которое каждой функции из множества М ставит в соответствие функцию из множества N .

Примеры операторов

Пример 1. Пусть М – множество функций, дифференцируемых n раз.

Нахождение первой производной – оператор над множеством функций М, обозначают его D или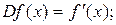

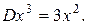
Нахождение второй производной – также оператор, обозначают его 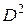 или

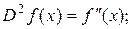
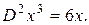
Нахождение n-й производной – оператор, обозначают его 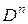 или

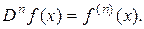
Пример 2. Однократное, двукратное, n-кратное интегрирование – операторы, для которых употребляются символы 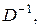…  или

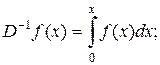
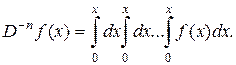
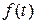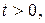
Пример 3. Пусть  – функция вещественного аргумента  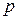  – комплексное число;  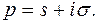Если сходится  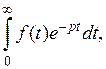то он является некоторой функцией аргумента p: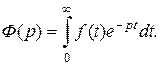

Интеграл, стоящий справа, называется интегралом Лапласа. Преобразование, по которому функции 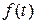 ставится в соответствие функция , называется преобразованием или интегральным оператором Лапласа.

Пример 4. Пусть  дважды дифференцируемая функция и

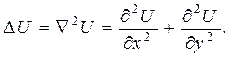
Преобразование, по которому функции U ставится в соответствие функция 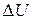, называется дифференциальным оператором Лапласа.

Действия над операторами

Над операторами можно производить арифметические операции.

Сумма двух операторов K ₁ и K ₂ определяется соотношением

Произведение операторов K ₁ и K ₂ определяется соотношением

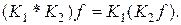
Если K ₁ и K ₂ равные операторы, 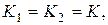 то их произведение обозначают K ².

Оператор, от применения которого функция не изменяется, называется единичным, обозначается символом E: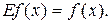

Два оператора называются взаимно обратными, если их произведения дают единичный оператор, т.е. если 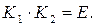 Для взаимно обратных операторов приняты обозначения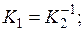

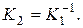
Определение 2.2 . Оператор K называется линейным, если он обладает двумя свойствами:

1) аддитивности: ;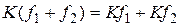

2) однородности: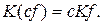

Все указанные в примерах операторы являются линейными.

2.2. Преобразование Лапласа и его свойства