Оператор Лапласа-Карсона – линейный оператор.
а) Проверим, что этот оператор обладает свойством аддитивности.
Обозначим 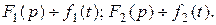 Найдем изображение функции
Найдем изображение функции  Тогда имеем:
Тогда имеем:
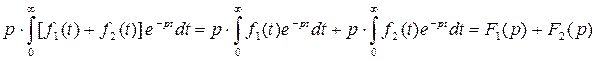 ,
,
или 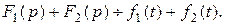
б) Проверим, что оператор Лапласа-Карсона обладает свойством однородности. Обозначим  Найдем изображения функции
Найдем изображения функции 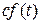 , где с – постоянная величина.
, где с – постоянная величина.
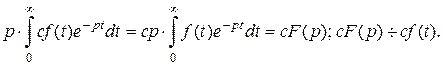
Так как оператор Лапласа-Карсона обладает свойствами аддитивности и однородности, то он является линейным оператором.
Правила операционного исчисления
Сложение
Так как преобразование Лапласа-Карсона – операция линейная, то очевидно, что из

следует
 .
.
Изображение суммы равно сумме изображений. Оригинал суммы равен сумме оригиналов.
Изображение постоянной
Изображение постоянной равно ей самой. Действительно, 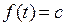 ;
; 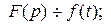
 при
при 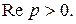
Изменение масштаба (теорема подобия)
Пусть 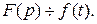 Как изменится изображение, если его аргумент умножится на число
Как изменится изображение, если его аргумент умножится на число 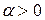 ? Обозначим
? Обозначим  Тогда
Тогда
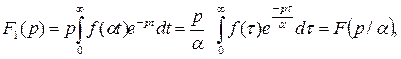
 где
где 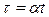 .
.
Итак,  .
.
Если  является аналитическим выражением некоторого колебательного процесса, то теорема подобия позволяет найти изображение при изменении частоты оригинала.
является аналитическим выражением некоторого колебательного процесса, то теорема подобия позволяет найти изображение при изменении частоты оригинала.
Дифференцирование оригинала
Пусть  Каково изображение
Каково изображение  ?
?
Обозначим 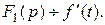 Тогда
Тогда
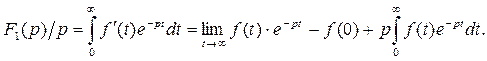
Если  – функция с ограниченным ростом, то
– функция с ограниченным ростом, то 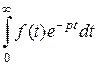 сходится при всех p,
сходится при всех p,  , где
, где  – показатель роста
– показатель роста 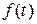 . Но это возможно, только если
. Но это возможно, только если 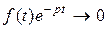 при
при 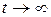 , а тогда
, а тогда 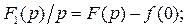

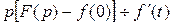 , где
, где 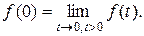
Если  то
то  Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Пусть  . Найдем изображение функции
. Найдем изображение функции 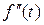 , воспользовавшись свойством дифференцирования оригинала.
, воспользовавшись свойством дифференцирования оригинала.
Обозначим 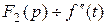 . Тогда
. Тогда
 , или
, или 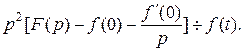
Если при  то
то 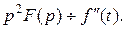
Аналогично можно найти изображение производной любого порядка.
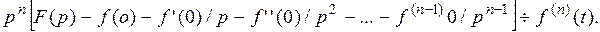
Если при 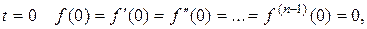 то
то 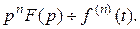
Следовательно, если функция  удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на
удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на  .
.
Интегрирование оригинала
Пусть 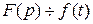 . Каково изображение
. Каково изображение 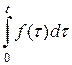 ? Обозначим его через
? Обозначим его через  т.е.
т.е. 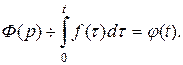 Продифференцируем
Продифференцируем 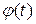 .
.
Пусть 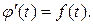 Но
Но  , поэтому
, поэтому 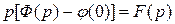 . Остаётся
. Остаётся 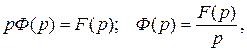 при
при 
Итак, 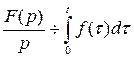 , т.е. при интегрировании оригинала от нуля до t изображение делится на p.
, т.е. при интегрировании оригинала от нуля до t изображение делится на p.
Найдем изображение для неопределенного интеграла (первообразной) 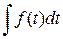 =
= 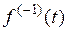 . Определенный интеграл
. Определенный интеграл 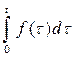 также является первообразной для функции
также является первообразной для функции  , поэтому
, поэтому  . Положив
. Положив 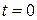 , получим
, получим 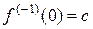 .
.
Тогда  , где
, где 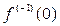 – постоянная.
– постоянная.
Изображение функции 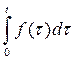 найдено ранее, поэтому
найдено ранее, поэтому
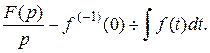
Дифференцирование изображения
Пусть 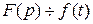 , т.е.
, т.е. 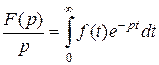 . (2.3)
. (2.3)
Продифференцируем обе части равенства (2.3) по параметру p.
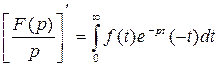 , или
, или 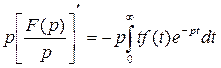 . Тогда
. Тогда
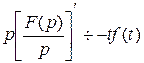 .
.
Продифференцируем обе части равенства (3.1) дважды по параметру p.
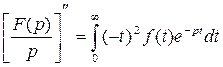 , или
, или 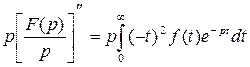 .
.
Следовательно, 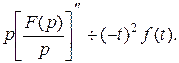

 Продифференцировав равенство (3.1) по параметру p n раз, получим:
Продифференцировав равенство (3.1) по параметру p n раз, получим:
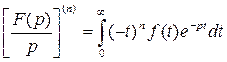 , или
, или 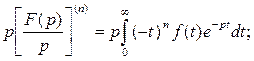
 , где
, где  – целое.
– целое.
Изучим поведение интеграла Лапласа при 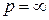 .
.
Теорема 2.3
Если  – функция с ограниченным ростом,
– функция с ограниченным ростом,  , то
, то  при
при  .
.
Доказательство
Пусть  , тогда
, тогда  .
.
Рассмотрим сколь угодно малое 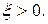 Покажем, что можно указать такое p, с достаточно большой вещественной частью
Покажем, что можно указать такое p, с достаточно большой вещественной частью 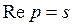 , для которого
, для которого
 В равенстве для
В равенстве для 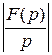 разобьём интеграл, стоящий справа, на два интеграла:
разобьём интеграл, стоящий справа, на два интеграла:
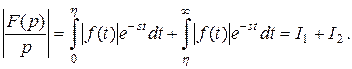
Рассмотрим 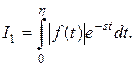 Так как
Так как 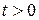 , то для тех p, для которых
, то для тех p, для которых 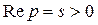 ,
, 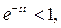 следовательно,
следовательно, 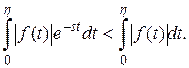 Подберём
Подберём  так, чтобы интеграл
так, чтобы интеграл 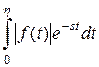 был меньше
был меньше 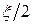 . Это возможно, потому что функция
. Это возможно, потому что функция 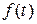 непрерывна или кусочно-непрерывна при
непрерывна или кусочно-непрерывна при 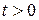 и
и 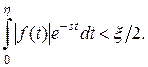
Рассмотрим 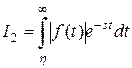 , где
, где  – функция с ограниченным ростом,
– функция с ограниченным ростом, 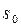 – показатель роста. Рассмотрим
– показатель роста. Рассмотрим 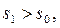
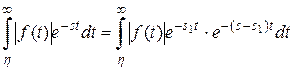 . Функция
. Функция  при
при  , наибольшее значение на промежутке
, наибольшее значение на промежутке 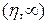 имеет при
имеет при  . Интеграл
. Интеграл 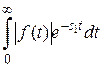 сходится, т.к.
сходится, т.к.  – функция с ограниченным ростом, а
– функция с ограниченным ростом, а 
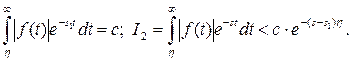
Здесь c, s1 и 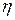 -фиксированные величины, а переменная s произвольная. Взяв
-фиксированные величины, а переменная s произвольная. Взяв 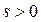 и достаточно большим, получим:
и достаточно большим, получим: 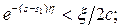
 т.к.
т.к.  - убывающая функция аргумента s.
- убывающая функция аргумента s.
Итак, при достаточно больших 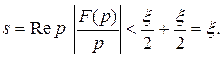 Рассуждения справедливы для любых
Рассуждения справедливы для любых 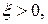 сколь угодно малых. Следовательно, выполняется неравенство:
сколь угодно малых. Следовательно, выполняется неравенство:  при
при 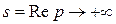 .
.
Теорема смещения
Теорема 2.4 (смещения)
Если  , то
, то 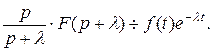
Доказательство
Пусть  . Найдем изображение функции
. Найдем изображение функции 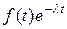 .
.
Обозначим 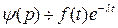 , тогда
, тогда
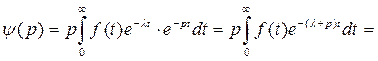

Отсюда 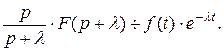 Предполагается, что
Предполагается, что 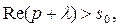 т.е.
т.е.
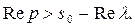
Название теоремы объясняется её геометрической интерпретацией.
Если p – вещественная переменная, то при умножении оригинала на  график изображения смещается на -
график изображения смещается на - 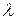 по оси p. Ординаты графика при
по оси p. Ординаты графика при
этом умножаются на 
2.4. Преобразование некоторых употребительных функций
Дата: 2019-02-19, просмотров: 327.