Квантовая химия, по сравнению с кинетикой и термохимией, предоставляет новые возможности для изучения химических реакций, позволяя расчетным путем восстановить ненаблюдаемое экспериментально движение реагирующей системы между реагентами и продуктами. Специфика квантовохимического подхода состоит в том, что реакционная способность системы характеризуется здесь разностью энергий особых точек на поверхности потенциальной энергии, тогда как в термохимии и кинетике – изменением термодинамических функций и константой скорости реакции, измеренными при определенных условиях. Схема сравнения данных этих подходов представлена на Рис. 1 для реакций между молекулами идеальных газов.
Рассмотрим, какие величины и как следует рассчитывать, чтобы описать химические реакции и корректно сравнить результаты теоретических расчетов с экспериментом.
Прежде всего принимают приближение Борна-Оппенгеймера и определяют поверхность потенциальной энергии (ППЭ) химической реакции как совокупность точек, характеризуемых определенной энергией системы при фиксированном положении ядер. Размерность пространства, в котором определяется ППЭ, для N взаимодействующих частиц задается числом координат, принятых в качестве степеней свободы плюс 1 (энергия): 3N – 5 (3N – 4). Из всех этих координат может быть выделена одна, задающая путь химической реакции - минимальный по энергии путь, непрерывно соединяющий долину исходных веществ и долину продуктов через точку локального максимума – переходное состояние или активированный комплекс. Эта координата называется координатой реакции.
| Уравнение Шредингера для электронов и ядер |
Приближение Борна-Оппенгеймера
| Электронное уравнение Шредингера. Уравнения Хартри-Фока. |
Теория молекулярных орбиталей
| Функция потенциальной энергии основного состояния реагирующей системы. |
Оптимизация геометрии
| Геометрия и энергия равновесного состояния реагирующей системы. | Геометрия и энергия переходного состояния реагирующей системы. |
Разделение колебаний и вращений
| Моменты инерции | Силовые постоянные |
| Вращательные энергетические уровни реагирующей системы | Колебательные энергетические уровни реагирующей системы |
Статистическая термодинамика
| Трансляционная функция распределения реаги рующей системы. | Вращательная функция распределения реагирующей системы | Колебательная функция распределения реагирующей системы | Энергия нулевых колебаний реагирующей системы |
| Энтальпия, энтропия, теплоемкость,... | Энтальпия активации, энтропия активации,... |
Методы термохимии Методы кинетики
Рис. 1. Приближенная схема вычисления термодинамических и кинетических параметров реагирующих молекул идеальных газов по их молекулярным свойствам. Жирным шрифтом выделены промежуточные результаты вычислений, курсивом – приближения или (и) методы их получения.
Для количественного описания реакций интерес представляют одно- и двумерные сечения ППЭ. Часто достаточно информативны детали ППЭ вдоль координаты реакции. Рассмотрим сечение ППЭ вдоль координаты реакции электрофильного замещения в ароматическом кольце в пара-положении по отношению к заместителю Х (Рис. 2).
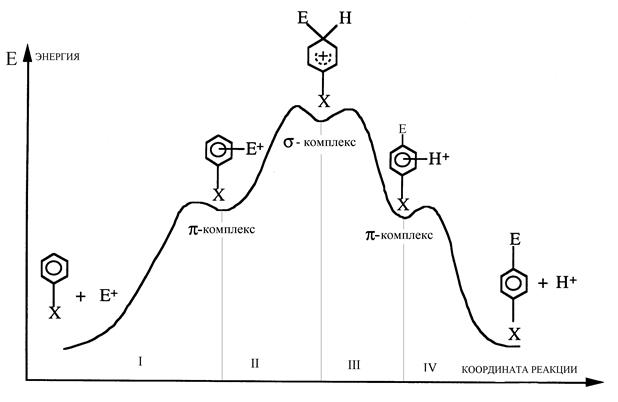
Рис. 2. Энергетический профиль ППЭ вдоль координаты реакции замещения в ароматическом кольце. Цифры нумеруют четыре стадии реакции.
Минимумы ППЭ соответствуют наблюдаемым в ходе реакции равновесным состояниям -бесконечно удаленным реагентам и продуктам, а также нестабильным интермедиатам, одномерные максимумы (седловые точки) – переходным состояниям. По количеству седловых точек ППЭ можно выделить четыре стадии рассматриваемой реакции. На стадии I между p -электронной системой ароматического кольца и электрофилом Е+ происходит образование неспецифического p -комплекса донорно-акцепторного типа. На стадии II образуется специфический s -комплекс (интермедиат Уэланда), в котором атом углерода ароматического кольца в пара-положении по отношению к заместителю Х связан, и с электрофилом Е+, и с уходящим протоном Н. На стадии III между p -электронной системой замещенного ароматического кольца и уходящим протоном Н+ происходит образование неспецифического p -комплекса донорно-акцепторного типа. На стадии IV p -комплекс распадается на продукты реакции.
Элементарный акт химической реакции.
В квантовой химии каждую стадию реакции принято рассматривать как элементарный акт. Пример такого рассмотрения для элементарного акта некоторой многостадийной реакции представлен на Рис. 3. Сечение ППЭ вдоль координаты реакции для элементарного акта (в общем случае) содержит 5 особых точек :
1. Бесконечно удаленные реагенты;
2. Предреакционный комплекс – ван-дер-ваальсов или со специфическими взаимодействиями;
3. Переходное состояние;
4. Послереакционный комплекс – ван-дер-ваальсов или со специфическими взаимодействиями;
5. Бесконечно удаленные продукты.
Характеристиками реакционной способности системы являются разности энергий этих особых точек, относящиеся к Т = 0К:
1. Энергия активации D Е* - разность полных энергий переходного состояния АВ* и предреакционного комплекса АВ (или бесконечно удаленных реагентов);
2. Энергия активации Еа0 - D Е* с учетом энергии нулевых колебаний Енк ;
3. Тепловой эффект химической реакции D Н - разность полных энергий после- и предреакционного комплексов CD и АВ;
4. Тепловой эффект химической реакции D Нр* - разность полных энергий продуктов C + D и реагентов А + В;
5. Тепловой эффект химической реакции D Н0- D Н с учетом энергии нулевых колебаний Енк после- и предреакционного комплексов CD и АВ;
6. Тепловой эффект химической реакции D Нр - D Нр* с учетом энергии нулевых колебаний Енк продуктов C + D и реагентов А + В.
Енк – разность энергий низшего колебательного состояния гармонического осциллятора (при значении полного колебательного квантового числа, равном 0) и минимума ППЭ, соответствующего рассматриваемому состоянию системы.
Эти энергетические характеристики реагирующей системы обычно используют для расчета термодинамических и кинетических параметров. Рассмотрим связь расчетной энергии активации с получаемой косвенным образом из эксперимента величиной ЕаТ- параметром уравнения Аррениуса. Это уравнение определяет установленную обобщением экспериментальных данных температурную зависимость константы скорости химической реакции k(T):
k(T) = A * exp(-ЕаТ / RT), 1)
R – универсальная газовая постоянная. С другой стороны, в теории абсолютных скоростей химических реакций (согласно Эйрингу) k(T) определяется уравнением (смотри, например, Эмануэль Н.М., Кнорре. Д.Г. Курс химической кинетики, 1984, М: Высшая школа, 463 с.):
k(T) = (kБT/h) * (Q*(T) / QАВ(T)) *exp(-ЕаТ / RT) , (2)
где h – постоянная Планка, kБ - постоянная Больцмана, Q*(T) и QАВ(T) - полные статистические суммы переходного состояния и предреакционного комплекса соответственно. QАВ(T) приближенно может быть заменена произведением статистических сумм свободных реагентов П Qi(T).
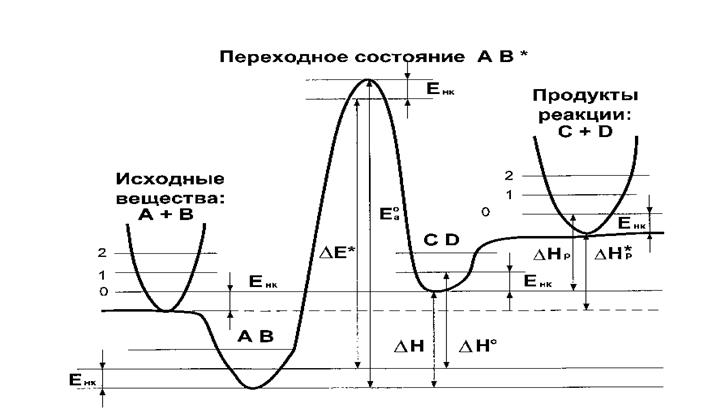
Рис. 3. Энергетический профиль ППЭ вдоль координаты реакции для элементарного акта некоторой многостадийной реакции.
В термодинамике статистическими суммами принято характеризовать вероятность пребывания системы в определенных поступательных, колебательных и вращательных состояниях, причем
Q(T) = Qпоступ.(T) Qколеб.(T) Qвращ.(T), (3)
где Qпоступ.(T), Qколеб.(T), Qвращ.(T) - поступательная, колебательная и вращательная статистические суммы, рассчитываемые по стандартным формулам (смотри, например, Краснов К.С. Физическая химия. Ч. 2. 1997, М.: Высшая школа.)
ЕаТ в (2)– энергия активации, рассчитываемая как разность между низшими энергетическими уровнями переходного состояния и реагентов с учетом температурной поправки и энергии нулевых колебаний Енк (см. Рис. 3).
Сопоставляя (1) и (2), можно заключить, что параметр ЕаТ уравнения Аррениуса для температурной зависимости константы скорости k(T) имеет смысл энергии активации химической реакции. Сравнение экспериментальной величины ЕаТ с расчетной величиной D Е* может быть осуществлено с учетом температурной поправки:
ЕаТ = D Е* + a RT (4)
(a =1 для мономолекулярных и Ѕ для бимолекулярных реакций). Сравнение ЕаТ с расчетной величиной Еа0 возможно с учетом поправки на энергию нулевых колебаний переходного состояния Енк* и предреакционного комплекса АВ ЕнкАВ (или бесконечно удаленных реагентов) :
D Е* = Еа0 + Енк* - ЕнкАВ , (5)
Еа0 = U* - UAB . (6)
Здесь U*, UAB – потенциальная энергия переходного состояния и предреакционного комплекса в равновесной конфигурации ядер.
Энергия нулевых колебаний определяется уравнением :
Енк = NA * S hn i , (7)
i
где NA – число Авагадро, n i – частоты гармонических колебаний при значении полного колебательного квантового числа, равном 0.
Уравнения (1)-(6) позволяют заключить, что энергия активации химической реакции ЕаТ, полученная косвенным путем из эксперимента, должна сравниваться с величинами Еа0 и D Е*, полученными в результате квантовохимических расчетов и исправленными на нулевые колебания (Еа0) и на температуру процесса (D Е*).
Современная экспериментальная техника лазерной импульсной спектроскопии предоставляет возможность прямого измерения энергии активации. Правда, в настоящее время она приложима лишь к весьма узкому кругу реакций, связанных с разрывом выделенной локализованной связи в молекуле (например, ICF3 (hn ) à I* + CF3 *). Лазер на СО2 позволяет осуществлять накачку определенного колебательного состояния молекулы (в рассматриваемом примере – валентного колебания связи СI). В этом случае энергия активации реакции разрыва связи (СI) характеризуется числом квантов электромагнитного излучения, после поглощения которого молекулой (ICF3) наблюдается образование продуктов реакции (I* + CF3 *).
Расчет поверхности потенциальной энергии химической реакции состоит в расчете оптимальной геометрии и энергии равновесных и переходного состояний и пути реакции. На Рис. 4 - 6 представлены примеры сечений ППЭ для реакций обмена и изомеризации. Изолинии на двумерных сечениях ППЭ соединяют точки с одинаковыми значениями энергии. Путь химической реакции во всех случаях проходит через энергетическую ложбину ППЭ. Он соединяет два локальных минимума, отвечающих реагентам и продуктам реакции через одномерный максимум. Одномерному максимуму соответствует переходное состояние (на двумерных плоских сечениях Рис. 4, б) и Рис. 5, а) переходное состояние обозначено крестиком).
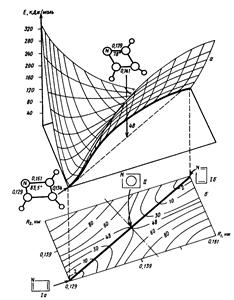
На Рис. 4 представлен общий вид ППЭ простейшей реакции обмена между атомом А и молекулой ВС : А + ВС à АВ + С. При коллинеарном сближении реагентов ППЭ определяют всего две внутренние координаты : межъядерные расстояния RАВ и RВС, что допускает достаточно строгие ее расчеты. Относительное расположение локальных минимумов ППЭ, соответствующих реагентам и продуктам, и седловой точки переходного состояния определяется тем, является ли рассматриваемая реакция обмена экзотермической (например, F + H2 à HF + H), эндотермической или теплонейтральной (например, Н + Н2 à H2 + H).
На Рис. 5 изображена ППЭ экспериментально пока не известной молекулы азациклобутадиена, отражающая ее предсказываемую вырожденную изомеризацию. На двумерном сечении ППЭ в координатах R1 и R2 (длинах ординарной и двойной связей CN) (Рис. 5, а)) наблюдаются два локальных минимума, отвечающие стабильным изомерам молекулы. Путь реакции проходит через переходное состояние с выравненными связями CN. Координата реакции (Рис. 5 , б)) есть функция координат R1 и R2.

Рис. 4 Двумерное сечение ППЭ для реакции обмена А + BС à AB + C :
а) объемное, б) плоское.
а) б)
Рис. 5 Сечения ППЭ для реакции изомеризации молекулы азациклобутадиена: а) двумерное объемное и плоское в координатах R1 и R2 – длинах ординарной и двойной связей CN, соответственно. б) одномерное, вдоль координаты реакции – линейной комбинации координат R1 и R2.
На Рис. 6 представлена ППЭ реации изомеризации 2-фторэтильного катиона. Экспериментально было установлено, что катионы такого типа являются нестабильными интермедиатами реакции электрофильного присоединения к двойной связи СС при протекании ее по ионному механизму. Теоретические исследования были направлены, главным образом, на установление структуры этих катионов и относительной устойчивости их изомерных форм. ППЭ, изовраженная на Рис. 6, обнаруживает интересную особенность : путь реакции соединяет циклическую и нециклическую формы 2-фторэтильного катиона через два последовательных переходных состояния.
Расчет особых точек ППЭ осуществляется в предположении о том, что реагентам, продуктам, пред- и послереакционным комплексам соответствуют локальные минимумы, а переходному состоянию - седловая точка ППЭ (Рис. 7).

Рис. 6. ППЭ реакции изомеризации 2-фторэтильного катиона как функция двух угловых переменных q и j .
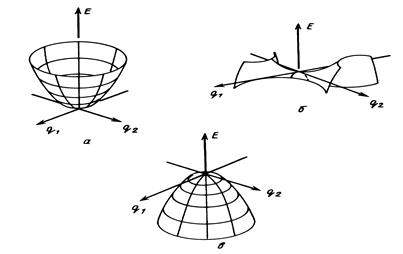
Рис. 7. Особые точки ППЭ : локальный минимум а), седловая точка б), двумерный максимум в).
Эти точки являются стационарными точками ППЭ. В минимуме производная от потенциальной энергии по всем координатам (градиент энергии) равна нулю:
¶ U/¶ Qi = 0, i = 1, 2,…, 3N-6(5), (8)
а все собственные значения матрицы вторых производных от потенциальной энергии по координатам (матрицы Гессе или гессиана) G положительны:
Gij = ¶ U2/¶ Qi¶ Qj > 0, i, j = 1, 2,…, 3N-6(5). (9)
Qi, Qj. – нормальные колебательные координаты.
Наиболее эффективными методами поиска стационарных точек являются методы градиентного или скорейшего спуска в минимум, такие как метод Дэвидона-Флетчера-Пауэлла, Ньютона, Ньютона-Рафсона, изучавшиеся в курсе вычислительной математики. Суть поиска сводится к тому, что задается начальное приближение к геометрии молекулы, которая затем оптимизируется итерационным путем. На каждой итерации каждая i-ая варьируемая координата атома (α, β=x, y, z) меняется на величину, называемую шагом. Шаг прямо пропорционален первой производной ¶ U/¶ αi (градиенту энергии) и обратно пропорционален сумме по j элементов гессиана S ¶ U2/¶ αi¶ βj . Направление скорейшего спуска определяется знаком градиента энергии. Отсюда и название методов. Вычисления завершаются, когда сумма абсолютных величин всех первых производных ¶ U/¶ αi становится меньше некоторого малого значения e . В современных программных комплексах обычно используется значение 10-5. Кроме того контролируется выполнение теоремы Гельмана-Фейнмана и теоремы вириала. Реальное время расчета определяется качеством геометрии нулевого приближения.
Многообразие вариантов метода скорейшего спуска обусловлено наличием разных способов расчета градиента и гессиана скалярных функций. На ППЭ, близких к параболическим, все градиентные методы обеспечивают квадратичную сходимость результата. Спуск в минимум независимо от формы ППЭ обеспечивает только метод Ньютона (требующий значительных затрат машинного времени). Если же ППЭ имеет участки с малой кривизной, что часто бывает, например, в окрестности переходных состояний реакций с переносом протона, любой из методов, кроме метода Ньютона, может привести к расходимости или к осциллирующему характеру итерационного процесса.
Хорошее приближение для начальной геометрии равновесных состояний молекул и молекулярных комплексов, участвующих в реакции, дают рентгено- и электроноструктурный анализ или спектроскопические структурные исследования. Геометрия переходного состояния может быть, в принципе, получена методом импульсного структурного анализа, использующего синхротроны и координатные детекторы.
Путь химической реакции.
Неоднократные попытки разработать общий алгоритм для локализации переходного состояния привели к концепции пути химической реакции. Согласно классическому определению Эйринга и Поляни (1931 г.), путь химической реакции - это путь минимальной энергии реакции, соединяющий соседние минимумы ППЭ через седловую точку переходного состояния. Путь минимальной энергии на сечениях ППЭ реакции обмена обозначен штриховой линией (Рис. 4), реакции изомеризации молекулы азациклобутадиена – жирной сплошной линией (Рис. 5). На сечении ППЭ реакции изомеризации 2-фторэтильного катиона (Рис. 6) из ряда альтернативных вариантов может быть выбран единственный путь минимальной энергии, соединяющий локальные минимумы двух метастабильных изомеров через два последовательные переходные состояния.
На основе определения пути минимальной энергии реакции был развит метод координаты реакции : сложным характером реакции пренебрегают и выделяют один структурный параметр, монотонное варьирование которого должно описывать ход реакции энергетическим профилем (типа представленного на Рис. 5, б)). Однако оказалось, что этот метод работает только в случае мономолекулярных реакций диссоциации или образования выделенной локализованной связи и в случае бимолекулярных SN2 реакций, в которых разрыв и образование связи происходит синхронно. В остальных случаях координата реакции является линейной комбинацией структурных параметров реагирующей системы. Представление ее единственным параметром может привести к серьезной ошибке : не имеющему физического смысла гистерезису путей прямой и обратной реакций ( например, реакция СН2 + Н2 ß à CH4). Суть сказанного поясняется на примере гипотетической реакции А ß à B.
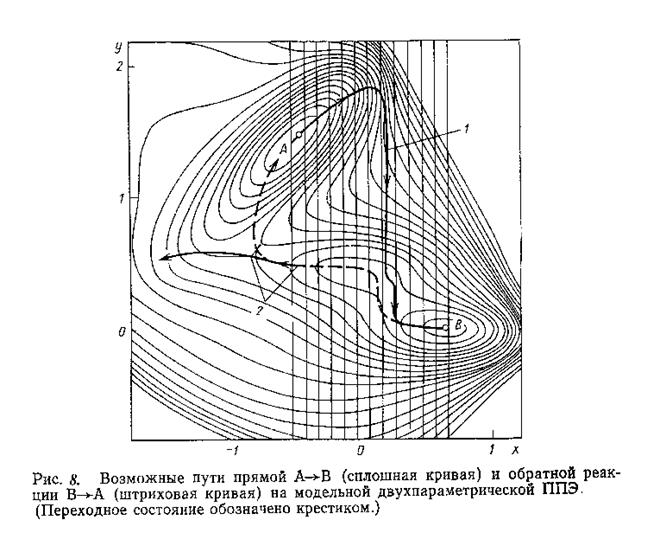
На Рис. 8 представлена двухпараметрическая ППЭ реакции А ß à B. Выберем в качестве координаты реакции параметр х. Если двигаться из локального минимума А, на каждом шаге увеличивая координату х и минимизируя энергию по параметру у, то мы получим энергетическую кривую, изображенную жирной линией, которая не проходит через переходное состояние. Если аналогичным образом двигаться в обратном направлении из минимума В, постепенно уменьшая координату х, то в минимум А мы не попадем вообще. Путь реакции, изображенный пунктирной линией, является функцией двух переменных х и у.
Позже, в качестве пути реакции предлагалось рассматривать путь градиентного или скорейшего спуска, возникающий при оптимизации геометрии реагирующей системы по упомянутым выше методам градиентного спуска. На основе этих представлений был развит метод Мак-Ивера, используемый в ряде современных квантовохимических программных комплексов, таких как MOPAC и GAMESS.
 В этом методе локализация переходного состояния осуществляется, исходя из того, что ему отвечает точка локального максимума на ППЭ, удовлетворяющая условию (5.8). Основным отличием этого метода от метода Дэвидона-Флетчера-Пауэлла является изменение знака градиента в уравнениях метода скорейшего спуска, обеспечивающее движение к максимуму ППЭ. К сожалению, (8) является необходимым, но не достаточным условием того, что найденная точка будет отвечать одномерному максимуму. Таким образом, без определения собственных значений гессиана (9) этот метод не гарантирует локализацию переходного состояния.
В этом методе локализация переходного состояния осуществляется, исходя из того, что ему отвечает точка локального максимума на ППЭ, удовлетворяющая условию (5.8). Основным отличием этого метода от метода Дэвидона-Флетчера-Пауэлла является изменение знака градиента в уравнениях метода скорейшего спуска, обеспечивающее движение к максимуму ППЭ. К сожалению, (8) является необходимым, но не достаточным условием того, что найденная точка будет отвечать одномерному максимуму. Таким образом, без определения собственных значений гессиана (9) этот метод не гарантирует локализацию переходного состояния.
Камнем преткновения в развитии концепции пути химической реакции явилась обнаруженная неинвариантность этого пути относительно ортогонального преобразования координат. При этом инвариантными оказываются только стационарные точки ППЭ. Поэтому в настоящее время в квантовой химии реакций фигурирует теория переходного состояния, рассматривающая только стационарные точки ППЭ.
Дата: 2019-02-19, просмотров: 546.