Таким образом, для изучения электронных состояний и свойств химических систем, необходимо решить уравнение Шредингера. Решения ищут с помощью вариационного принципа, минимизируя энергию системы и определяя функции, максимально близкие к собственным функциям оператора Н. Вариационный принцип утверждает, что среднее значение энергии Е_i любого из возможных i состояний системы не может быть меньше нижнего собственного значения Е₀ оператора Н. Покажем это.

Среднее значение оператора Н для некоторой волновой функции Y , нормированной на 1, равно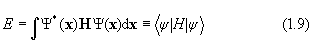

Представим Y в виде разложения по собственным функциям оператора Н:

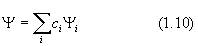
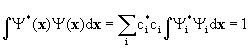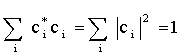что всегда возможно, поскольку последние составляют полную ортонормированную систему. В силу этого или . Подставляя (1.10) в (1.9), имеем:

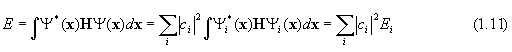
где Е_i - энергия i-го состояния. Ясно, что 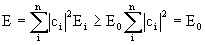, где Е₀ - нижнее собственное значения оператора Н, т.к. энергии возбужденных состояний выше, чем низшего, называемого основным, что и требовалось доказать.

Итак, чтобы решить уравнение Шредингера, нужно минимизировать выражение для энергии (1.9), т.е. подобрать такие волновые функции, для которых энергия будет минимальна. Для этого волновая функция должна включать некоторые переменные параметры, изменяя которые можно обеспечить минимум. Например, можно записать волновую функцию в виде линейной комбинации

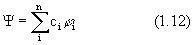
где j _i - n выбранных из некоторых соображений функций (например, для атомов - это могут быть атомные орбитали, о которых мы поговорим далее), часто называемые базисными, а c_i - переменные параметры. Чтобы найти минимум (1.9), нужно, чтобы все первые производные энергии по параметрам c_i равнялись нулю, а вторые - были положительны. Обычно, однако, ограничиваются равенством нулю первых производных, что отвечает условию стационарности:

¶ Е/ ¶ c₁ = ¶ Е/ ¶ c₂ = .... = ¶ Е/ ¶ c_n = 0 (1.13а)

¶ Е/ ¶ c₁^* = ¶ Е/ ¶ c₂^* = .... = ¶ Е/ ¶ c_n^* = 0. (1.13б)

На языке вариационного исчисления, обычно используемого в квантовой химии, это эквивалентно требованию обращения в нуль первой вариации 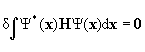. Из этого условия должен следовать набор уравнений, решая которые совместно, можно найти параметры c_{i .} При этом следует, однако, принять во внимание, что эти коэффициенты не независимы, а связаны в силу ортономированности функций Y соотношением:

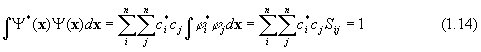
Интеграл 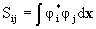называется интегралом перекрывания.

Для учета при минимизации ограничений, каковым является условие (1.14), математики используют метод неопределенных множителей Лагранжа. Вводя такой множитель Е, уравнение для определения параметров c_i представим в виде

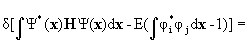
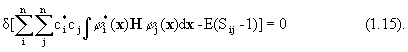
Теперь все параметры c_i можно считать независимыми. Кроме того, варьирование по 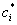ничего нового не дает по отношению к варьированию по 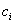: одни решения получаются из других сорпяжением. Поэтому производя варьирование только по вещественным параметрам, имеем в компактной записи:

_.

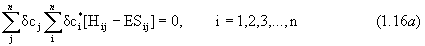
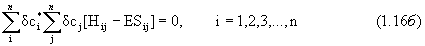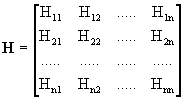
Здесь 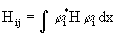- матричное представление оператора Н в базисе функций j _i , а S_ij - матрица интегралов перекрывания:

Поскольку все вариации в (1.16) независимы, это матричное уравнение справедливо лишь, если коэффициенты при вариациях равны нулю, т.е.

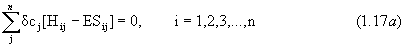
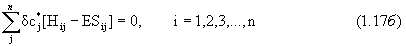
Поскольку уравнение 1.17б получается из уравнения 1.17а простой операцией комплексного сопряжения, впредь будем рассматривать только уравнение 1.17а.

Полученная система однородных линейных уравнений позволяет найти параметры c_i , обеспечивающих минимум функционала (1.9). Чтобы ее решить, необходимо приравнять нулю определитель (детерминант) из коэффициентов при c_i:

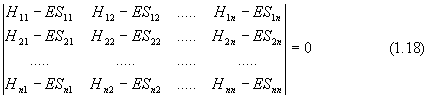
или в других обозначениях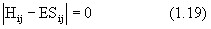

Уравнение (1.19) впервые возникло в задачах классической механики о вековых (секу-лярных) возмущениях планетарных орбит. Отсюда название - вековое или секулярное уравнение. При разложении определителя получается многочлен n-ой степени по Е, значит вековое уравнение имеет n корней (n различных значений Е), подставляя которые в (1.16), можно найти соответствующий набор параметров c_i . Величина Е играет роль энергии состояния системы.

Чтобы найти волновую функцию основного состояния, нужно взять наименьшее из полученных значений энергии, подставив его в (1.17), найти коэффициенты с_i, а затем и волновую функцию Y (1.12). Волновые функции возбужденных состояний ищут таким же образом.

Реализовать этот алгоритм точно возможно только для водородоподобного атома (иона). Этот вопрос подробно рассматривался в курсе физики. Однако атомы всех элементов, кроме водорода, многоэлектронные. Что же мешает найти для них точные волновые функции и уровни энергии? Дело в том, что если электронов больше одного, каждый из них движется уже не в поле ядра, а в поле, создаваемом ядром и остальными электронами. Точное решение уравнения Шредингера для таких систем уже невозможно; в операторе энергии взаимного отталкивания электронов (1.6) переменные разделить невозможно, поскольку эта энергия зависит от координат двух электронов одновременно. Это заставляет прибегать к различным приближениям, которые мы далее и рассмотрим.