Введение

Большинство открытий в области естественных наук связано с развитием представлений о строении и динамике окружающего нас мира. Важное место в этом процессе занимает квантовая теория материи. Квантовая химия является одним из частных аспектов этой теории. Эта фундаментальная дисциплина рассматривает приложение квантовомеханических законов к изучению химических явлений и процессов на атомно-молекулярном уровне.

Путь к познанию законов материального мира в атомно-молекулярной шкале был непрост и долог. Плоды его человечество получило не только в виде электронной, компьютерной, коммуникационной, космической и биомедицинской революций, приведших к качественно новой техносфере, окружающей человека, к расшифровке генома и клонированию живых существ, но и в виде ядерного, химического и бактериологического оружия. Какие же научные представления привели к столь радикальным переменам?

В 20-е годы нашего века описание материи основывалось на восходящей к Демокриту и Дальтону концепции атомов, каждый из которых состоит из отрицательно заряженных электронов и положительно заряженных ядер. Тому в подтверждение были получены хорошо понятные многочисленные экспериментальные данные, хотя законы, описывающие поведение электронов, были изучены слабо. Идея волнового характера микромира (де Бройль) сняла многие противоречия. Однако представления того времени не раскрыли причин образования молекул из атомов, специфики их поведения в основном состоянии и тем более в химических реакциях. Чтобы сделать это, потребовалась последовательная теория. Ею стала квантовая механика, обеспечившая методологию, способную описывать и предсказывать многие свойства веществ на атомном уровне. Со временем химики убедились в действенности этой методологии и это в корне изменило содержание многих химических исследований. Квантовая химия, рассматривая поведение электронов, объяснила строение химических соединений, природу химической связи, энергетику различных химических процессов, колебания, химические реакции и взаимодействия в сложных молекулярных ансамблях, включая биологические системы.

Курс квантовой химии в РХТУ, рассматривая атомы, молекулы и их ансамбли и кристаллы, опирается на постулаты квантовой механики, которые изучаются в курсах физики и теоретических основ химии. Для его изучения достаточно знакомства с математикой в стандартном вузовском объеме. Важнейшим в квантовой химии является понятие волновой функции - характеристики состояний химических систем, зависящей от координат частиц и являющейся решением уравнения Шредингера. Это уравнение волновые функции связывает с возможными значениями энергии состояний при заданном числе электронов и ядер и известном взаимном расположении последних. Зная волновые функции, можно определить распре-деление электронного заряда, рассчитать моменты молекулы, вычислить ее спекроскопические и резонансные характеристики, описать ее реакционную способность, рассчитать зонную структуру кристалла и т.д.

Для простых систем волновые функции рассчитывают численно, для систем более сложных и представляющих практический интерес для химиков это невозможно. Поэтому при расчетах приходится вводить различные приближения. Одним из основных таких приближений, используемом в большинстве квантовохимических расчетов, является приближение Борна-Оппенгеймера, основанное на идее раздельного рассмотрения волновых функций, описывающих состояния электронов и ядер. Более тяжелые ядра двигаются намного медленней электронов и при описании многих электронных процессов могут считаться неподвижными. В результате математическая задача определения электронных волновых функций сильно упрощается. Теория химической связи, например, построена именно в этом приближении.

Дальнейшие приближения касаются электронного движения. Отрицательно заряженные электроны отталкиваются в молекуле друг от друга. Это воздействует на их движение, которое, как говорят, является коррелированным. Именно это создает основную трудность в определении волновых функций для многэлектронных систем. Поэтому в большинстве методов квантовой химии исходят из приближения, что движение электронов некоррелировано и ищут волновые функции электронов, считая их независимыми. Поскольку, однако, все частицы в молекуле взаимодействуют, это учитывают, вводя для заданного электрона вместо мгновенного взаимодействия с другими электронами и ядрами, взаимодействие с полем, усредненным по положениям всех других частиц. Благодаря этому, проблема расчета волновых функций для сложных систем упрощается, поскольку задача сводится к определению одноэлектронных волновых функций каждой частицы в среднем поле остальных (молеку-лярных орбиталей). Один из наиболее мощных методов квантовой химии - метод Хартри-Фока- позволяет рассчитать именно такие функции.

Хотя приближение независимых частиц - довольно серьезное упрощение, к счастью, во многих случаях оно допустимо и позволяет, найдя волновые функции, понять химическое поведение молекулы. Учет корреляций в движении электронов возможен, хотя и сложен, при этом опять приходится привлекать различные приближениия. Чаще всего корреляция учитывается по теории возмущений, используя хартри-фоковскую волновую функцию как исходное приближение, или путем представления волновой функции в виде суперпозиции более простых волновых функций, описывающих возможные возбуждения в системе.

Часто для понимания сути химических процессов или трактовки экспериментальных данных достаточно использовать менее точные и весьма упрощенные подходы. Промежуточные величины, фигурирующие в схеме расчета, в этих методах рассматриваются как параметры, извлекаемые. как правило, из эксперимента. Такие методы называются полуэмпирическими; они различны для разных классов соединений и их использование требует отдельного изучения. Такие методы важны, потому что, несмотря на многие достижения, идеи квантовой химии в чистом виде (ab initio) непосредственно применимы к ограниченному классу химических проблем: затраты на вычисление волновых функций быстро растут с размером системы. Более того, в важных химических процессах, протекающих в биологических системах, типа метаболизма в организме человека, участвуют функциональные фрагменты, составленные из многих тысяч атомов, которые в свою очередь, окружены меньшими молекулами. Потребность в изучении таких сложных "макромолекулярных" систем привела к развитию полуклассических моделей, которые объединяют описание атомов в терминах электронов и ядер с простой моделью, основанной на классических физических законах (типа закона Ньютона). В этой схеме атомы рассматриваются как неделимые частицы, а взаимодействие между ними описывается упрощенными математическими соотношениями, следующими, однако, из квантовой химии. Этот подход называется молекулярной механикой, а ее раздел, изучающий как химическая система изменяется при движении атомов в поле соседей, - молекулярной динамикой. Параметры в такой классической модели получают, выполняя квантовохимические вычисления намного меньших систем. Такое моделирование способно объяснить механизм многих химических явлений и процессов.

При рассмотрении процессов, в которых химические связи образуются и разрушаются, приходится комбинировать классический и квантовый подходы, рассматривая части системы, в которых происходят химические изменения, квантово, а их взаимодействия с окружением - классически. Чтобы сделать это на практике, необходимо глубокое понимание предела при-менимости каждого метода, опирающееся на квантовохимические знания. Такой подход, в частности, применяется при исследовании биологических систем и при изучении селективных, экстракционных и каталитических процессов, Так, способность катализаторов управлять реакцией обусловлена свойствами среды, окружающей "активный участок" реакции. Без учета влияния окружающей среды, которой, например, может быть, поверхность фермента в белках или полость в цеолитах, способность катализатора управлять ходом реакции понять невозможно. Методы моделирования, пригодные к рассмотрению этих сложных химических систем, помогают поиску новых химических агентов, включая лучшие катализаторы и более эффективные лекарства.

Какое еще научное и технологическое применение находит информация, получаемая в результате расчетов? Она необходима, например, для решения задач нелинейной оптики, в частности, фотоники - технологического аналога электроники, в котором вместо электронов для получения, хранения, передачи и обработки информации используются фотоны. Нелинейные оптические явления применяют для управления электронными свойствами сред, обеспечивающих изменение частоты (цвета), усиление и переключение излучения , используют в датчиках, основанных на изменении свойств материалов под действием давления, темпера-турных, электрических полей, и т.д. Оптимизация оптических нелинейностей материалов на молекулярном уровне требует детального понимания соотношения между электронной струк-турой и нелинейной поляризацией вещества. Квантовохимические методы обеспечивают это, позволяя предсказать свойства оптических материалов (поляризуемости, гиперполяризуемости) и оценить способность отклика среды на приложенное электромагнитное воздействие. Точность метода обеспечивает решение даже этой специфической задачи, требующей знания поведения волновых функций как основного, так и возбужденных состояний.

Квантовая химия в комбинации с физической и коллоидной химией и биохимией сыграла важную роль в появлении молекулярных компьютерных и материаловедческих технологий в наношкале - нанотехнологий. Среди задач этого направления, решаемых методами квантовой химии, -характеристика наноматериалов микроскопического и объемного характера с особыми конструктивными, электрическими и тепловыми свойствами, моделирование программируемых молекулярных систем, способных самоорганизовываться и создавать новые материальные объекты, проектирование молекулярных и биологических систем и изделий различного назначения, включая компоненты компьютера, такие как память атомной плотности, и материалы космической техники (нанодизайн). Все эти проблемы связаны с изучением электронной структуры и свойств молекул, молекулярных ансамблей и кластеров и кристаллов.

Даже этот краткий обзор показывает как на наших глазах изменяется содержание химическо-технологических задач и какую роль в этом играет квантовая химия.

к разделу "Лекции"

на основную страницу предметной комиссии по квантовой химии

Принципы квантовой механики

Основой для изучения квантовой химии являются курсы “Теоретические основы химии”, "Высшая математика" и "Физика", которые изучаются в РХТУ в 1-4 семестрах. Напомним, что квантовая химия атомов, молекул и их ансамблей и кристаллов опирается на следующие основные постулаты квантовой механики:

1.Каждое состояние системы n частиц полностью описывается функцией координат частиц x и времени t Y ({x},t), называемой волновой функцией. Волновая функция существует во всем интервале изменения переменных, где она непрерывна, конечна и однозначна. Выражение 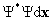имеет смысл вероятности того, что в момент времени t i-ая частица находится в интервале координат от x_i до x_i+dx_i , а интеграл 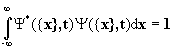, при условии, что волновые функции нормированы на единицу. Поскольку физический смысл имеет лишь величина Y^*Y, то волновая функция определена с точностью до произвольного фазового множителя типа e^ia .

2.Каждой доступной измерению величине А в любом из возможных состояний соответствует линейный эрмитов оператор А. Оператором называется символ, обозначающий математическую операцию, с помощью которой из одной функции получается другая; каждому оператору отвечает уравнение типа Аf=af, где а - вообще говоря комплексное число, называемое собственным значением оператора А, а f называется собственной функцией А. Оператор, обладающий свойством

,

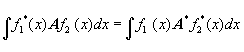называется эрмитовым; собственные значения эрмитовых операторов - действительные числа, а их собственные функции образуют полную ортонормированную систему, т.е. 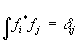. Действуя на волновую функцию, оператор превращает ее в другую волновую функцию; говорят, что действие оператора переводит систему в другое состояние (частный случай - система остается в том же состоянии).

Таблица 1.1. Операторы основных физических величин

Переменная	Обозначение переменной	Обозначение оператора	Производимая операция
Координата	r	r	Умножение на r
Момент	p	p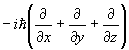
Кинетическая Энергия	T	T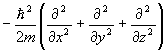
Потенциальная энергия	V(r)	V(r)	Умножение на V(r)
Полная энергия	E	H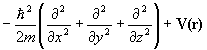

3. Независящая от времени волновая функция удовлетворяет стационарному уравнению Шредингера:

H Y = ЕY (1.1).

Здесь H=T+V- эрмитов оператор полной энергии системы (гамильтониан) есть сумма оператора кинетической энергии всех частиц системы Т и оператора их потенциальной энергии V, Е - полная энергия системы. Квантовая химия изучает свойства атомов, молекул и кристаллов, состоящих из положительных ядер и отрицательных электронов, потенциальная энергия которых определяется кулоновским взаимодействием. Операторы кинетической энергии в системе М ядер и N электронов выглядят так:

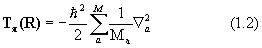
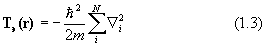
Здесь M_a – масса ядра a; m - масса электрона;

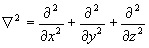- оператор Лапласа (лапласиан).

Дифференцирование в уравнении (1.2) ведется по координатам ядер, в (1.3) – по координатам электронов.

Вид операторов потенциальной энергии (в системе СИ) следующий:

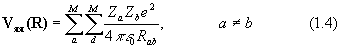
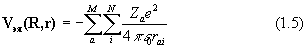
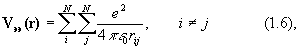
где Z_a и Z_b - атомный номер элемента, e - заряд электрона, R_ab – расстояние между ядрами, r_ij – расстояние между электронами.

Оператор (1.4) описывает отталкивание ядер, (1,5)– энергию притяжения электронов к ядрам, (1.6) – отталкивание электронов.

Строго говоря, в гамильтониане следует учесть релятивистские эффекты, обусловленые близкой к световой скоростью электронов в низкоэнергетических состояниях (электронов остова), спин-орбитальным взаимодействием и взаимодействием Дарвина, возникающим вследствие малых флуктуаций движущихся электронов относительно средних позиций. Однако, в очень хорошем приближении их можно игнорировать при рассмотрении многих квантовохимических задач, за исключением тяжелых (Z > 18) атомов и их ансамблей.

Зависящая от времени волновая функция удовлетворяет нестационарному уравнению Шредингера .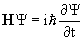

4. Значения величины А, которые могут быть измерены, являются собственными значениями а_i уравнения на собственные значения

А Y_i = а_iY_i , (1.7а)

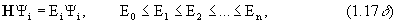
где собственная функция Y _i есть волновая функция, описывающая возможные состояния системы, в которых проводятся измерения. Это означает, что решение уравнения Шредингера (1.1) есть не что иное как решение задачи на собственные значения оператора полной энергии системы Н. Спектр собственных значений и набор собственных функций гамильтониана полностью характеризуют систему.

5. Среднее значение <а> величины А для системы, находящейся в состоянии i, определяется выражением: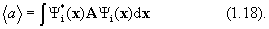

(предполагается, что волновые функции 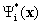ортонормальны). Это дает рецепт определения характеристик системы с помощью волновых функциий.