Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

КВАНТОВАЯ ХИМИЯ

Библиографический список

1. Цирельсон В.Г., Бобров М.Ф., Апостолова Е.С., Михайлюк А.И. Лекции по квантовой химии. РХТУ, 1998. –350 с.

2. В.И. Минкин, Б.Я. Симкин, Р.М. Миняев. Теория строения молекул. Ростов-на-Дону “Феникс”, 1997 – 560 с.

3. Р. Заградник, Р. Полак. Основы квантовой химии. М: Мир, 1979.

4. Дж. Марелл, С.Кеттл, Дж.Теддер. Химическая связь. М: Мир, 1980.

5. К.С. Краснов. Строение молекул и химическая связь. М: Высшая школа, 1985.

6. В.Г. Цирельсон. Химическая связь и тепловое движение атомов в кристаллах. -М.: Винити, 1993.

7. И.Б. Берсукер. Электронное строение и свойства координационных соединений. Л: Химия, 1986.

ЛЕКЦИИ

Лекции 1-4 КВАНТОВАЯ ХИМИЯ АТОМА

Введение. Предмет квантовой химии и ее роль в описании химических явлений и процессов. Принципы квантовой механики.

Вариационный принцип. Решение уравнения Шредингера. Приближение независимых частиц. Метод самосогласованного поля. Приближение центрального поля. Атомные орбитали и их характеристики. Антисимметричность электронной волновой функции. Детерминант Слейтера. Метод Хартри-Фока. Ограниченный и неограниченный методы Хартри-Фока.

Квантовохимическая трактовка решений уравнений Хартри-Фока. Электронные конфигурации атомов с точки зрения квантовой химии.

Лекции 5-8 КВАНТОВАЯ ХИМИЯ МОЛЕКУЛЫ

Приближение Борна-Оппенгеймера. Метод Хартри-Фока для молекул. Приближение МО ЛКАО. Уравнения Рутана. Ограничения метода ХФ.

Электронная корреляция. Метод конфигурационного взаимодействия. Теорема Бриллюэна. Теория возмущений. Метод валентных связей. Точность учета электронной корреляции. Расчет энергии диссоциации химических связей.

Иерархия методов квантовой химии. Неэмпирическая квантовая химия. Базисные функции для неэмпирических расчетов. Вид аналитических базисных функций. Номенклатура базисных наборов. Минимальный базисный набор. Расширенный базисный набор. Поляризационные и диффузные функции. Базисные наборы Попла. Роль базисных функций в описании свойств молекул.

Метод полного пренебрежения дифференциальным перекрыванием. Метод частичного (промежуточного) пренебрежения дифференциальным перекрыванием (INDO). Метод модифицированного частичного пренебрежения дифференциальным перекрыванием (MINDO). Метод модифицированного пренебрежения дифференциальным перекрыванием. Разделение s - и p -электронов. p -электроннное приближение. Метод Парризера-Попла-Парра. Метод МО Хюккеля. Расширенный метод Хюккеля. Точность квантовохимических расчетов химических свойств молекул.

Лекции 9-12.ХИМИЧЕСКАЯ СВЯЗЬ И МЕЖМОЛЕКУЛЯРНОЕ ВЗАИМОДЕЙСТВИЕ

Орбитальная картина химической связи. Конструктивная и деструктивная интерференция орбиталей. Молекулярные орбитали и их симметрийная классификация. Электронные конфигурации двухатомных молекул. Анализ заселенностей орбиталей по Малликену. Понятие о зарядах и порядках связей.

Пространственное распределение электронной плотности. Деформа-ционная электронная плотность. Топологическая теория химической связи. Электростатический и энергетический аспекты описания химической связи.

Описание электронной плотности в многоатомных молекулах. Локализация и гибридизация орбиталей. Орбитальное обоснование модели отталкивания электронных пар Гиллеспи и строение молекул. Химическая связь в координационных соединениях. Теория кристаллического поля и теория поля лигандов. Спектрохимический ряд. Комплексы сильного и слабого полей. Магнитные свойства комплексов. Энергия стабилизации кристаллическим полем. Теория поля лигандов. Эффект Яна-Теллера.

Квантовохимический анализ межмолекулярных взаимодействий. Оценка ван-дер-ваальсовых атомных радиусов. Донорно-акцепторные молекулярные комплексы. Специфические невалентные взаимодействия. Водородная связь.

Понятие о супрамолекулярной химии.

Лекции 13-14 КВАНТОВОХИМИЧЕСКОЕ ОПИСАНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ

Квантовохимическое описание химических реакций в газовой фазе. Поверхность потенциальной энергии (ППЭ) химической реакции. Путь химической реакции, координата реакции. Переходное состояние, активированный комплекс. Расчет поверхности потенциальной энергии химической реакции. Особые точки равновесных и переходных состояний. Расчет реагентов, продуктов, перед- и послереакционных комплексов. Правило Вудворда-Хоффмана. Методы описания химических реакций: теория возмущений, метод координаты реакции, метод граничных молекулярных орбиталей Фукуи.

Орбитальные модели взаимодействия молекул с поверхностью. Хемосорб-ция.

Лекции 15-16.ЭЛЕКТРОННАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ

Одноэлектронные волновые функции в кристаллах и методы их расчета. Приближение локальной плотности. Уровень Ферми. Плотность состояний. Зонная структура твердых тел и обусловленные ею свойства. Хa - метод. Кластерное приближение и его применение в квантовой химии координационных соединений.

ЗАКЛЮЧЕНИЕ. Квантовая химия как инструмент прогноза в химии.

СЕМИНАРСКИЕ ЗАНЯТИЯ

1. Атомные орбитали и их свойства. Энергии одноэлектронных состояний .

2. Молекулярная структура. Конформации молекул. Молекулярные орбитали.

3. Химическая интерпретация результатов квантовохимических расчетов.

Специфика неэмпирических и полуэмпирических методов. Источники

квантовохимической информации в ИНТЕРНЕТ.

4. Химическая связь в двухатомных молекулах.

Принципы квантовой механики

Основой для изучения квантовой химии являются курсы “Теоретические основы химии”, "Высшая математика" и "Физика", которые изучаются в РХТУ в 1-4 семестрах. Напомним, что квантовая химия атомов, молекул и их ансамблей и кристаллов опирается на следующие основные постулаты квантовой механики:

1.Каждое состояние системы n частиц полностью описывается функцией координат частиц x и времени t Y ({x},t), называемой волновой функцией. Волновая функция существует во всем интервале изменения переменных, где она непрерывна, конечна и однозначна. Выражение 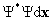имеет смысл вероятности того, что в момент времени t i-ая частица находится в интервале координат от x_i до x_i+dx_i , а интеграл 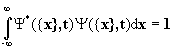, при условии, что волновые функции нормированы на единицу. Поскольку физический смысл имеет лишь величина Y^*Y, то волновая функция определена с точностью до произвольного фазового множителя типа e^ia .

2.Каждой доступной измерению величине А в любом из возможных состояний соответствует линейный эрмитов оператор А. Оператором называется символ, обозначающий математическую операцию, с помощью которой из одной функции получается другая; каждому оператору отвечает уравнение типа Аf=af, где а - вообще говоря комплексное число, называемое собственным значением оператора А, а f называется собственной функцией А. Оператор, обладающий свойством

,

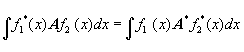называется эрмитовым; собственные значения эрмитовых операторов - действительные числа, а их собственные функции образуют полную ортонормированную систему, т.е. 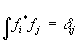. Действуя на волновую функцию, оператор превращает ее в другую волновую функцию; говорят, что действие оператора переводит систему в другое состояние (частный случай - система остается в том же состоянии).

Таблица 1.1. Операторы основных физических величин

Переменная	Обозначение переменной	Обозначение оператора	Производимая операция
Координата	r	r	Умножение на r
Момент	p	p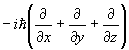
Кинетическая Энергия	T	T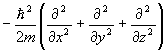
Потенциальная энергия	V(r)	V(r)	Умножение на V(r)
Полная энергия	E	H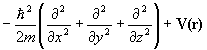

3. Независящая от времени волновая функция удовлетворяет стационарному уравнению Шредингера:

H Y = ЕY (1.1).

Здесь H=T+V- эрмитов оператор полной энергии системы (гамильтониан) есть сумма оператора кинетической энергии всех частиц системы Т и оператора их потенциальной энергии V, Е - полная энергия системы. Квантовая химия изучает свойства атомов, молекул и кристаллов, состоящих из положительных ядер и отрицательных электронов, потенциальная энергия которых определяется кулоновским взаимодействием. Операторы кинетической энергии в системе М ядер и N электронов выглядят так:

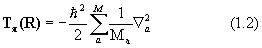
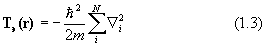
Здесь M_a – масса ядра a; m - масса электрона;

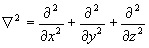- оператор Лапласа (лапласиан).

Дифференцирование в уравнении (1.2) ведется по координатам ядер, в (1.3) – по координатам электронов.

Вид операторов потенциальной энергии (в системе СИ) следующий:

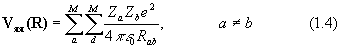
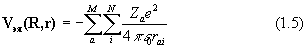
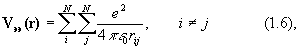
где Z_a и Z_b - атомный номер элемента, e - заряд электрона, R_ab – расстояние между ядрами, r_ij – расстояние между электронами.

Оператор (1.4) описывает отталкивание ядер, (1,5)– энергию притяжения электронов к ядрам, (1.6) – отталкивание электронов.

Строго говоря, в гамильтониане следует учесть релятивистские эффекты, обусловленые близкой к световой скоростью электронов в низкоэнергетических состояниях (электронов остова), спин-орбитальным взаимодействием и взаимодействием Дарвина, возникающим вследствие малых флуктуаций движущихся электронов относительно средних позиций. Однако, в очень хорошем приближении их можно игнорировать при рассмотрении многих квантовохимических задач, за исключением тяжелых (Z > 18) атомов и их ансамблей.

Зависящая от времени волновая функция удовлетворяет нестационарному уравнению Шредингера .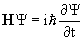

4. Значения величины А, которые могут быть измерены, являются собственными значениями а_i уравнения на собственные значения

А Y_i = а_iY_i , (1.7а)

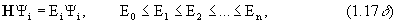
где собственная функция Y _i есть волновая функция, описывающая возможные состояния системы, в которых проводятся измерения. Это означает, что решение уравнения Шредингера (1.1) есть не что иное как решение задачи на собственные значения оператора полной энергии системы Н. Спектр собственных значений и набор собственных функций гамильтониана полностью характеризуют систему.

5. Среднее значение <а> величины А для системы, находящейся в состоянии i, определяется выражением: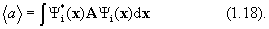

(предполагается, что волновые функции 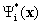ортонормальны). Это дает рецепт определения характеристик системы с помощью волновых функциий.

Детерминант Слейтера

Итак, представление многоэлектронной волновой функции в виде детерминанта обеспечивает ее правильные антисимметричные свойства. Кроме того, электроны неразличимы и их перестановка не должна менять свойства системы. Перестановка электронов для детерминанта эквивалентна перестановке местами столбцов (строк), что лишь меняет знак детерминанта. Поскольку волновая функция в принципе определена с точностью до фазового множителя, перемена знака свойств системы не меняет. Приближенная многоэлектронная волновая функция, построенная из ортонормированных спин-орбиталей отдельных электронов, называется детерминантом Слейтера:

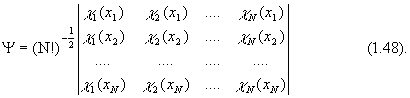
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции в орбитальном приближении. Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений.

Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается "своей" волновой функцией. Системы, в которых все электроны спарены на орбиталях, называются системами с закрытыми (или замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами спин-орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.

Метод Хартри-Фока

Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера (1.48) и использование приближения самосогласованного поля приводят к методу Хартри-Фока (ХФ). При этом исходное электронное уравнение Шредингера (1.20) путем довольно громоздких математических вычислений (см., например, М.Дьюар. Теория молекулярных орбиталей в органической химии) преобразуется в уравнения, где точный гамильтониан H (1.20) заменен оператором Фока (фокианом):

F = 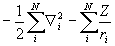+ 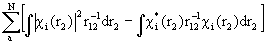(1.49)

(Здесь и далее мы используем принятую в квантовой химии атомную систему единиц: множитель 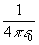опускается, m = 1, e = 1, 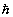=1. Введение атомных единиц делает формулы менее громоздкими).

Различие между F и H состоит в том, что оператор кулоновского межэлектронного взаимодействия 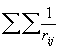заменен оператором в квадратных скобках, описывающим взаимодействие каждого электрона со средним полем всех остальных электронов с учетом требований принципа Паули. Из условия минимума энергии 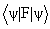возникает набор независимых уравнений для каждой одноэлектронной орбитали - уравнения Хартри-Фока:

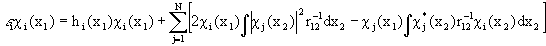1.50

Энергия электрона, находящегося на орбитали 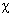_i, может быть получена умножением слева выражения (1.50) на 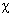_i и интегрированием по всему пространству:

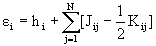(1.51),

где 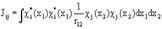, (1.52),

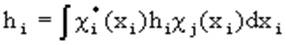(1.53),

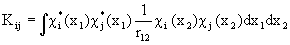. (1.54)

Одноэлектронный интеграл 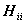описывает энергию электрона на орбитали 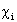в поле ядра без остальных электронов.

Двухэлектронный кулоновский интеграл 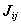описывает энергии межэлектронного отталкивания при независимом движении электронов.

Двухэлектронный обменный интеграл 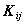отражает понижение энергии электронов с параллельными спинами на орбиталях 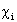и .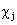

Полная энергия атома с замкнутыми оболочками (по 2 электрона на каждой орбитали) вычисляется в методе ХФ следующим образом:

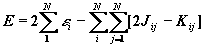(1.55)

Подчеркнем, что оператор Фока сам зависит от полного набора одноэлектронных волновых функций и его решение ищется самосогласованно. По этой причине метод ХФ иногда отождествляют с методом ССП. Поскольку, однако, общая стратегия самосогласования проявляется в квантовой химии во многих контекстах, название "метод Хартри-Фока" более точно.

Оператор Фока состоит из трех членов:

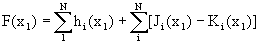(1.56)

Здесь h_i - точный одноэлектронный оператор (1.22):

h_i = - 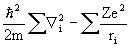(1.57)

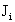- кулоновский оператор:

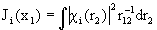(1.58)

и 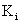- нелокальный обменный оператор:

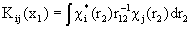(1.59)

Наличие обменного члена в методе ХФ эквивалентно введению поправки на корреляцию движения электронов, описываемых разными орбиталями. Другими словами, этим мы учитываем корреляцию между движением электронов с разными спинами (обменную корреляцию). Кулоновская корреляция, вызванная взаимным отталкиванием электронов, независимо от их спинов, в методе ХФ не учитывается: она является следствием приближения независимых частиц. Это - существенный недостаток метода и мы к нему еще вернемся. Кроме того, в противоположность точной волновой функции, однодетерминантная функция ХФ вследствие самосогласования не имеет сингулярности при |r_i - r_j|® 0, следующей из (1.6).

Уравнения ХФ могут, в принципе, быть решены численно любым стандартным методом решения интегро-дифференциальных уравнений (например, методом Монте Карло, методом сетки и др.).

Квантовая химия молекул

Введение

Квантовая химия рассматривает молекулу как образование из точечных ядер и электронов с целочисленными массами и зарядами. Энергия молекулы имеет составляющие, связанные с кинетическими энергиями каждого электрона и ядра и попарными энергиями их кулоновских взаимодействий (Табл.2.1). Это должно быть надлежащим образом отражено в математическом формализме, описывающем строение и свойства молекул.

Табл. 2.1. Вклады в молекулярную энергию фтористого водорода HF

в равновесной геометрии

Составляющие энергии	Значение энергии (а.е.)	Вклад в полную энергию
Кинетическая Tэ	99.85594	100%
N-e ПритяжениеVэя	-250.58398	-251%
e-e Отталкивание + Обмен	45.49697	46%
N-N Отталкивание Vяя	5.22817	5%
Полная энергия	-100.00290	-100%

Основное уравнение молекулярной квантовой химии - независящее от времени нерелятивистское уравнение Шредингера:

· · НY ({r, R})=ЕY ({r, R}), (2.1)

Здесь H-молекулярный гамильтониан, E-полная энергия молекулы, Y ({r,R}) - молекулярная волновая функция, с помощью которой в принципе могут быть рассчитаны химические свойства молекулы. Символом {r, R} обозначена совокупность координат всех электронов и ядер.

Нерелятивистский гамильтониан молекулы включает члены, описывающие все перечисленные выше вклады в энергию, и имеет вид

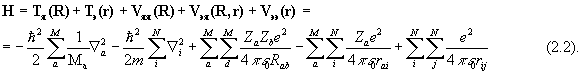
Здесь i, j относятся к электронам и a, b - к ядрам, M_а и m - массы ядер и электронов, R и r - наборы ядерных и электронных координат, спин-орбитальным взаимодействием пренебрегаем. В дальнейшем изложении для простотымы будем использовать атомную систему единиц, полагая е=1, m=1, 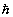=1. Множитель 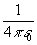в этой системе не возникает.

Ограничения метода ХФ

В ряде молекулярных задач, решаемых методом ХФ, проявляется так называемая "дилемма симметрии". Дело в том, что из-за нелинейности уравнений ХФ среди решений всегда имеются такие, симметрия которых отличается от симметрии ядерной конфигурации молекулы. Класс однодетерминантных функций, обладающих надлежащей симметрией, всегда уже, чем при отсутствии симметрийных ограничений. Последние же дают более низкое значение энергии из-за дополнительной вариационной свободы. Таким образом, в вариационной процедуре возникает дилемма: что лучше - более низкая энергия или правильная симметрия орбиталей? Пример: Для правильного шестиугольника Н₆ при больших расстояниях между атомами существуют решения, обладающие симметрией относительно 3-го, а не 6-го порядка. Такая же ситуация встречается в полиенах.

Метод ХФ также непригоден для расчета энергии Ферми в металлах.

Ограничения метода ХФ

В ряде молекулярных задач, решаемых методом ХФ, проявляется так называемая "дилемма симметрии". Дело в том, что из-за нелинейности уравнений ХФ среди решений всегда имеются такие, симметрия которых отличается от симметрии ядерной конфигурации молекулы. Класс однодетерминантных функций, обладающих надлежащей симметрией, всегда уже, чем при отсутствии симметрийных ограничений. Последние же дают более низкое значение энергии из-за дополнительной вариационной свободы. Таким образом, в вариационной процедуре возникает дилемма: что лучше - более низкая энергия или правильная симметрия орбиталей? Пример: Для правильного шестиугольника Н₆ при больших расстояниях между атомами существуют решения, обладающие симметрией относительно 3-го, а не 6-го порядка. Такая же ситуация встречается в полиенах.

Метод ХФ также непригоден для расчета энергии Ферми в металлах.

Теория возмущений

Теория возмущений является мощным приемом при решении многих квантовохимических проблем. Она использует тот факт, что в ряде задач фигурируют разные по порядку величины и, отбрасывая малые величины, задачу можно сильно упростить. Тогда гамильтониан Н можно представить в виде суммы гамильтониана более простой "невозмущенной" системы Н₀ и малого возмущения Н':

Н = Н₀ + Н' . (2.24)

Уравнение Шредингера имеет вид

Н Y = (Н₀ + Н')Y = ЕY . (2.25)

Предполагается, что уравнение Шредингера для Н₀ (т.е. для более простой системы) решено, т.е. известны все собственные функции { Y ₀ } и энергии {Е₀ }. Чтобы найти поправки, связанные с возмущеним, представим Y ₁ в виде разложения по ортономированным невозмущенным функциям Y ₀:

Y ₁ = å _m c_{mY m,0} (2.26)

и его подставим в (2.25):

å _m c_m (Н₀ + Н') Y _m,0 = å _m c_mЕY _m,0 (2.27)

Домножим обе части полученного уравнения на Y _k,0^* и проинтегрируем. Учитывая ортонормированность функций Y _m,0 имеем:

(Е- Е_0,k)c_k = å _m c_m ò Y _к,0Н'Y _m,0 dx , (2.28)

Разложим теперь энергию Е и коэффициенты c_m в степенные ряды:

Е = Е₀ + Е₁ + Е₂ + … ( 2.29)

c_m = c_m,₀ + c_m,₁ + c_m,₂ + ... .

Величины с индексом "1" имеют тот же порядок малости, что и возмущение Н', с индексом "2" - второго порядку малости и т.д. Найдем поправки к n-му собственному значению и собственной функции, для чего положим c_n =1, c_m=0, m ¹ n. Поправка первого порядка получается, если подставить Е = Е₀ + Е₁ и c_m = c_m,₀ + c_m,₁ в (2.28). При k=n имеем:

Е_n,1 = Н'_nn = ò Y _n,0Н'Y _n,0 dx , (2.30)

т.е. поправка к энергии первого порядка Е_n,1 = Н'_nn определяется через невозмущенные волновые функции и матричный элемент оператора возмущения.

При k¹ n

c_k,1 = Н'_kn/ (Е_n,0 - Е_r,0), k¹ n. (2.31)

Коэффициент c_n должен быть выбран так, чтобы функция Y _n = _{Y n,0} +Y _n,1 была нормирована с точностью до членов 1-го порядка, для чего следует положить c_n,1 = 0. Тогда поправка 1-го порядка к волновой функции равна

Y _n,1 =å '_m [Н'_mn/ (Е_n,0 - Е_m,0)] Y _n,0 (n¹ m) (2.32)

Отсюда хорошо видно условие применимости теории возмущений:

Н'_mn << ê Е_n,0 - Е_{m,0 ê} , (2.33)

т.е. матричные элементы возмущения должны быть меньше, чем разность энергий невозмущенных электронных уровней. Аналогичным образом находят поправки второго порядка:

Е_n,2 =å '_m ê Н'_{kn ê} ²/ (Е_n,0 - Е_m,0), (2.34)

Y _n,1=å '_må '_k{{[Н'_mn Н'_kn/(Е_n,0 - Е_m,0)(Е_n,0 - Е_k,0)]}-

{Н'_km Н'_kn/(Е_n,0 - Е_k,0)²}Y _n,0 (n¹ m, k¹ n) (2.35)

Поправка второго порядка к энергии основного состояния всегда отрицательна, поскольку значение Е_n,0 согласно вариационному принципу минимально. Приведенные результаты получены для дискретного спектра значений энергии. Их, однако, можно обобщить и на непрерывный спектр. Таким образом, теория возмущений применима к широкому кругу вопросов. Многочастичная теория возмущений дает подход к описанию электронной корреляции. В этом подходе разница между точным гамильтонианом Н и гамильтонианом нулевого порядка Н₀ рассматривается как возмущение:

Н= Н₀ + Н' = Н_ХФ + Н'. (2.36)

Вычисление среднего значения энергии для точного гамильтониана с волновой функцией вида (2.36) ведет к той же иерархии уравнений для волновой функции и энергии, что описана выше. Поправки могут быть сделаны в любом порядке энергии и волновой функции. Если H₀ - оператор Фока, мы приходим к теории возмущений Меллера-Плессета (MPPT), где самая низкая отличная от нуля поправка к энергии ХФ имеет второй порядок (MP2). MP2-приближение довольно надежно, не имеет недостатков метода КВ и по времени расчета близко к методу ХФ. Поэтому здесь допустимо использование довольно широкого базиса (6-31G* или шире – см. ниже) с включением поляризационных и диффузных функций. Более высокие уровни MP теории возмущений уже сложны и требуют большого компьютерного времени. Например, MP2 расчет энергии молекулы пентана C₅H₁₂ в базисе 6-31G+d (99 базисных функций) требует в 4 раза больше времени, чем расчет по методу ХФ; MP4 требует уже в 90 раз больше времени. Конечно, сходимость MP - разложения может сильно меняться от молекулы к молекуле. Недостатки: теория возмущений MP дает невариационное решение, а потому полученное значение E_{корреляц.} может оказаться завышенным.

Метод валентных связей

Метод валентных связей (ВС) исторически является первым квантово-химическим методом: именно в его рамках Гайтлер и Лондон рассчитали в 1927 г. молекулу водорода. В этом методе учитывают, что атомы в молекулах сохраняют во многом свою индивидуальность, а эффект химической связи рассматривается как возмущение, приводящее к обмену электронами и их спариванию в соответствии с требованием принципа Паули. Поэтому многоэлектронная волновая функция Y строится как линейная комбинация линейно-независимых антисимметризованных произведений наборов АО со спиновыми частями, выбранными по специальным правилам:

Y = å _i c_{iY i} ^ВС (2.37)

Каждая функция Y _i ^ВС соответствует набору атомов в определенных электронных конфигурациях и называется валентной структурой (ВС). Параметры орбиталей в ВС и их веса c_i определяются с помощью вариационного принципа. Электронное строение и свойства системы, таким образом, представляются в методе ВС как среднее по различным ВС, число которых может быть очень велико (иногда, впрочем, для хорошего описания достаточно несколько ВС). На первых стадиях развития квантовой химии эта взвешенная суперпозиция валентных структур получила название резонансный гибрид, а сами ВС называются резонансными (или каноническими). Ни одна из резонансных структур не отвечает реально существующему состоянию молекулы - только их суперпозиция! Разложение на ВС - не более чем математический прием.

Метод ВС близок по духу методу КВ. Отличие состоит в том, что в методе ВС исходными "строительными блоками" многоэлектронных функций являются АО всех атомов, тогда как в методе КВ - МО. То обстоятельство, что ВС строятся из АО, отвечающих определенным электронным конфигурациям атомов, привело к понятию валентного состояния атома. Оно определяется как электронная конфигурация, "подготовленная" для вступления атома в химическую связь в том или ином соединении с минимальным изменением энергии. При этом часть валентных электронов оказывается неспаренными и волновая фунция атома не отвечает определенным значениям операторов L² , L_z , S² , S_z ^. Это означает, валентное состояние не есть стационарное или некоторое возбужденное состояние, а значит оно не будет спектроскопически наблюдаемым.

2.11 Точность учета электронной корреляции

Совершенствуя учет электронной корреляции и увеличивая размер и гибкость базисного набора, можно систематически улучшать квантовохимические результаты, приближаясь, в принципе, к точному ответу. Величины синглет-триплетного расщепления уровней метилена для разных методов и базисных наборов даны в таблице 2.8 (экспериментальное значение - 9.2 ккал/моль).

 

Таблица 2.8. Расчетные значения синглет-триплетного расщепления уровней метилена (ккал/моль), полученные разными методами в разных базисных наборах

Метод/ базис	6-31G	6-31G*	6-31G**	6-311 G**	6-311 ++G**	6-311++ (3df,2pd)
НХФ	33.9	27.6	27.6	26.0	25.5	24.7
ОХФ	36.8	30.9	30.9	29.3	28.8	28.1
MP2	28.7	20.8	20.1	18.0	17.4	15.0
MP3	26.4	18.3	17.5	15.3	14.8	12.6
MP4D	25.3	17.1	16.3	14.1	13.5	11.3
MP4DQ	25.4	17.3	16.6	14.4	13.9	11.8
MP4SDTQ	25.2	17.0	16.2	14.1	13.5	11.4

В тоже время, расчетные значения длин связей и валентных углов лишь слабо зависят от корреляционных эффектов (табл. 2.9).

Таблица 2.9. Ошибки в длинах связей и валентных углах, рассчитанных разными методами в DZP базисе (в сравнении с экпериментом)

Молекула	Связь/метод	HF	MP2	MP4
		Ошибка в длине связи (А)
H2O	O-H	-0.006	0.005	0.005
NH3	N-H	-0.011	0.002	0.004
CH4	C-H	-0.001	0.003	0.006
C2H2	C-H C-C	-0.002 -0.012	0.006 0.024	0.008 0.025
CH2O	C-H C=O	-0.005 -0.015	0.003 0.022	0.008 0.023
HCN	C-H C-N	-0.003 -0.017	0.004 0.032	0.006 0.030
HCN	N-H C-N	-0.008 -0.010	0.007 0.025	0.007 0.031
CO2	C-O	-0.015	0.022	0.028
Средняя ошибка		-0.009	0.013	0.015
		Ошибка в валентном угле ( град.)
H2O	H-O-H	2.1	-0.1	0.0
NH3	H-N-H	1.5	0.0	-0.3
CH20	H-C-O	-0.3	-0.2	-0.6
Средняя ошибка		1.3	-0.1	-0.3

Расширенный базисный набор

Чтобы добиться лучшего описания, используют большее количество функций на одну орбиталь: две, три и т.д. Соответственно, следуя Фудзинага и Даннингу, различают двух- (дубль-зета -DZ), трехэкспоненциальный (TZ) и т.д. базисы.

При образовании химической связи валентные орбитали атомов более подвержены воздействию других атомов, чем внутренние (остовные) орбитали. Поэтому для их описания требуются большее количество базисных функций. Соответствующие базисные наборы называются расщепленно-валентными (SV). Это не значит, что валентные орбитали включают большее количество примитивов. С другой стороны, орбитали остова часто представляют собой длинные СОГТ, состоящие из многих примитивов, поскольку требуется обеспечить граничные условия на ядре для функции s- типа (см. выше).

Базисные наборы Попла

Иное соглашение было принято Дж. Поплом с сотрудниками, внесшими огромный вклад в развитие неэмпирических расчетов и создавшими программу GAUSSIAN. Структура базисного набора дается для целой молекулы, а не для отдельных атомов (см. табл.2.11). Эти обозначения подчеркивают также расщепленный валентный (SV) характер этих наборов. Символы n-ijG или n-ijkG расшифровываются так: n - число примитивов для внутренних оболочек; ij или ijk - число примитивов для СОГТ в валентных оболочках. ij обозначения описывают валентные DZ наборы, ijk - валентные TZ наборы. Вообще, в базисных наборах, полученных группой Попла, s и p сжатия, принадлежащие к тот же самой " электронной оболочке" (то есть соответствующих формально одному и тому же главному квантовому числу n) оказываются свернутыми в sp-оболочки. В этом случае, число примитивов s-типа и p-типа одинаково и они имеют одинаковые экспоненты. Однако, коэффициенты для s- и p-типа сжатий различны.

Базисные наборы Попла могут также быть расширены за счет включения поляризационных функций d- типа только для неводородных атомов (n-ijG* или n-ijkG *) или p-функциями для атомов водорода (n-ijG ** или n-ijkG **). В метане 4-31G* отражает следующее расщепление ( 431,31,1) / (31) или (8s, 4p, 1d/4s) ® [3s, 2p, 1d/2s], в то время как базис 6-311G ** для молекулы HCN включает следующие СОГТ: (6311,311,1) / (311,1) или (11s, 5p, 1d/5s, 1p) ® [4s, 3p, 1d/3s, 1p].

При введении диффузных функций используются следующие обозна-чения: n-ij+G, или n-ijk+G означает, что добавлен 1 диффузный гауссиан s-типа и p-типа к стандартному базисному набору для тяжелых атомов. В этом случае s- и p-типа функции имеют те же самые экспоненты. N-ij ++ G, или n-ijk ++ G получены добавлением 1 диффузного гауссиана s-типа и p-типа для тяжелых атомов и диффузного гауссиана 1 s-типа для водорода.

Табл.2.11. Некоторые рекомендуемые базисные наборы Попла

базисный набор	Описание	Число базисных функций Неводоро- дные ½ водород атомы
STO-3G	Минимальный базисный набор. Используется для получения полуколичественных результатов в больших системах.	5	1
3-21G	Двухэкспоненциальный базисный набор. Два набора функций для валентных электронов дают более точное представление орбиталей. Более прост,чем расчет с набором 6-31G(d) .	9	2
6-31G(d) [6-31G*]	Добавлены поляризационные функции для неводородных атомов. Исполь-зуется в большинстве расчетов систем средней сложности. (Включает 6 компонентов функций d-типа.)	15	2
6-31G(d,p) [6-31G**]	Добавлены также поляризационные функции водородов. Используется в случае, когда участие водородных атомов важно (пример - вычисление энергий связи) и для окончательных, точных вычислений энергии.	15	5
6-31+G(d) [6-31+G*]	Добавлены диффузные функции. Важно для систем с ионными парами, анионов, возбужденных состояний.	19	2
6-31+G(d,p) [6-31+G**]	Добавлены р-функции водорода. Используются, когда нельзя применить 6-31G(d,p) и необходимы диффузные функции.	19	5
6-311+G(d,p) [6-311+G**]	Трехэкспоненциальный базисный набор. Добавлены валентные функции (по три s- и p- функции) к 6-31+G(d,p). (Используются пять чистых d-функций)	22	6
Использование остальных базисных наборов позволяет выполнить наиболее точные вычисления
6-311+G(2d,2p)	Включает 2 d-функции неводородных атомов (плюс диффузные функции), и 2 р-функции водородов.	27	9
6-11+G(2df,2pd)	Включает 2 d-функции и 1 f-функцию неводородных атомов (плюс диффузные функции), и 2 р-функции и 1 d-функцию водородов.	34	14
6-1++G(3df,3pd)	Включает 3 d-функции и 1 f-функцию неводородных атомов, и 3 р-функции и 1 d-функцию водородов, также диффузные функции обоих.	39	18

Таблица 2.12. Рассчитанные в различных базисах и экспериментальные характеристики молекулы СО.

 

базис	Re .ae=1	w e см-1	De Эв	m 0a Дебай	Градиент электрического поля на ядре
					С	О
DZ	2.175	2003	10.196	+0.259	0.745	0.637
DZD	2.137	2179	11.817	-0.076	0.819	0.661
DZDF	2.136	2183	11.914	-0.072	0.845	0.700
TZ	2.182	1985	10.329	-0.060	0.921	0.606
TZD	2.139	2154	11.785	-0.230	0.985	0.676
TZDD	2.135	2152	11.808	-0.218	0.983	0.693
TZDF	2.132	2170	11.911	-0.197	1.001	0.730
TZDDF	2.132	2167	11.929	-0.220	1.002	0.730
QZ	2.177	2012	10.502	-0.104	0.858	0.571
QZDDF	2.132	2173	11.966	-0.243	0.980	0.744
Численный Набор ХФ	2.128	2174	12.084	-0.241	0.9691(5)	0.7559(5)
	2.13	2170	12.0	-0.24
эксперимент	2.132	2170	11.2	-0.122

R_e – равновесное межъядерное расстояние,

w _e – собственная частота колебаний,

D_e - энергия диссоциации,

m ₀^a – дипольный момент.

 

Молекула

ΔΗ

Геометрия. Å и градусы

Расчетная

Экспериментальная

Углы и связи

Расчетная

Экспериментальная

ккал/моль КДж/ моль ккал/моль КДж/ моль CH₃—CH₃ 19.8 —83.1 -20.2 —84.8 СС СН Ð ССН 1.486 1.108 112.8° 1.532 1.107 111.1° Н₂С==СН₂ 19.2 80.6 12.4 52.0 СС СН Ð ССН 1.308 1.098 124.8° 1.336 1.103 121.6° НС≡≡СН 57.8 242.7 54.3 228.0 СС СН 1.191 1.076 1.205 1.059 Н₂С=С=СН₂ 42.0 176.4 45.9 192.7 СС СН Ð НСС 1.311 1.099 118.4° 1.308 1.087 118.2°

58.1 244.0 71.1 298.5 С==С С—С СН Ð НСС q 1.344 1.466 1.109 115.7° 148.3° 1.340 1.476 1.100 117.б° 136.9° 34.1 143.2 34.6 145.3 CN С₂ С₃ С_З С₄ 1.335 1.407 1.406 1.340 1.395 1.394 -8.0 -33.6 —8.3 —34.8 СО С₂ С₃ С_З С₄ 1 .343 1.367 1.455 1.371 1.357 1.440

 

Перекрыванием (MNDO).

Чтобы более корректно учесть отталкивание неподеленных электронных пар, Дьюар с сотр. (1977) предложил включить в расчет все двухэлектронные интегралы, содержащие пары АО, принадлежащие одному и тому же атому; перекрывание АО различных атомов по-прежнему игнорирутся (приближение двухатомным дифференциальным перекрыванием). Модификация коснулась далее способа выбора параметров: в отличие от MINDO/3, они зависят только от свойств отдельных атомов, а не от их парных комбинаций. Это позволяет параметризовать метод по большему числу соединений, расширяя таким образом сферу его применимости.

В результате развития этого метода появились различные схемы, отли-чающиеся выбором параметров: AM1, AM3 (Austin Model), PM3 (Parameterised Model 3) и др. Они обеспечили возможность расчета водородной связи (AM3), а также энергии образования органических молекул и переходных состояний органических реакций (PM3) с ошибкой менее 5 ккал/моль.

2.21 Разделение s - и p -электронов. p -электроннное приближение

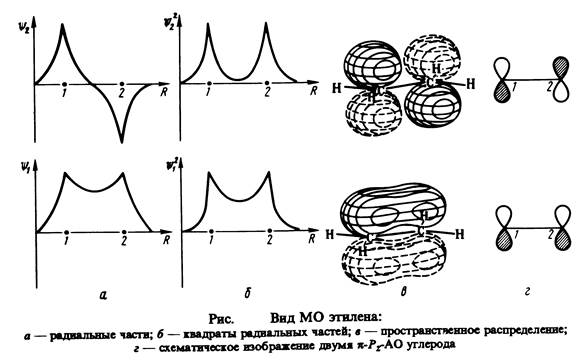При квантовохимических исследованиях ненасыщенных и ароматических молекул, чаще всего являющихся плоскими, как правило, используют s , p - приближение, состоящее в следующем. Для плоских молекул все валентные АО можно разбить на две группы. Одна из них содержит орбитали, симметричные относительно отражения в плоскости молекулы ( s -АО ), другая - орбитали, антисимметричные относительно такого отражения ( p -АО). Рис.2.7 иллюстрирует это на примере этилена. s -электроны имеют максимальную вероятность нахождения в плоскости молекулы и поэтому локализованы близ ее, вероятность нахождения здесь p -электронов, наоборот, равна нулю. p -электроны слабее связаны с остовом молекулы, более подвижны, легче ионизируются и более активны во взаимодействиях.

Свойства ненасыщенных и ароматических систем – высокая реакционная способность, зависимость от донорных и акцепторных заместителей, спектры и т.д – определяются, в основном, именно электронами, описываемыми p -орбиталями. Поэтому при решении уравнений Рутана для таких систем вводят p -электронное приближение (Хюккель, 1931): s -АО считают неполяризованными и включают в атомный остов, а движение p -электронов рассматривают в потенциальном поле таких остовов. Волновая функция молекулы при этом представляется как произведение y = y s _{y p} , где y s и y p - нормированные антисимметричные по отношению к s - и p -электронам функции, соответственно. Их можно разложить по слейтеровским детерминантам, составленных только из s - и только из p -МО. Волновая функция y s одинакова как для основного, так и для возбужденных состояний и все изменения связываются с p -электронами. Существенно, что рассмотрение только p -электронов удовлетворяет вариационному принципу (Мак-Вини, 1954; Лайкос и Парр, 1956).

В результате размерность уравнений Рутана сильно сокращается: например, для этилена вместо 12 валентных электронов необходимо учитывать только 2 p -электрона.

Метод Парризера-Попла-Парра

Объединение нулевого дифференциального перекрывания и p -электронного приближения приводит к методу Парризера-Попла-Парра, дающего прекрасные результаты для p -электронных систем. Матричные элементы оператора Фока для этого метода приведены в табл. 2.16. Um _m равно потенциалу ионизации атома в соответствующем валентном состоянии, взятому с обратным знаком: - Im . Одноцентровые кулоновские интегралы g m _m оцениваются по формуле Паризера-Парра (2.66). Величины Im и Am , необходимые для расчета Um _m и g m _m определяют из спектроскопических данных для валентных состояний атомов, используя модель локализованных связей. Двухцентровые интегралы g _AB рассчитывают по формулам (2.67)-(2.68). Величины hm n считаются параметрами и выбираются по разному для расчета свойств основного (метод Попла) и возбужденных (метод Парризера-Парра) состояний.

1. Для основного состояния hm n являются резонансными интегралами b m n = kSm n , где k подбирается так, чтобы наилучшим образом воспроизводить теплоты образования в представительном круге соединений (существует и ряд других параметризаций).

2) Для возбужденных состояний следует учесть, что волновая функция молекулы должна быть суммой волновых функций основного Y ₀ и возбужденных Y _{i® k} состояний: Y =Y ₀ + å а_{i® kY i® k}. Обычно учитывают несколько однократно возбужденных электронных конфигураций заданной мультиплетности и ищут коэффициенты а_{i® k} вариационным методом. Матричные элементы (Y _0ï h p ï Y ₀) дают энергию основного состояния Е₀, а элементы (Y _{i® kï} h p ï Y _{j® l}) имеют вид:

(Y _{i® kï} h p ï Y _{j® l})º hp _{i® k, j® l} = d _{kle k} - d _{ije i} +2(jkï li)-(jk ï il). (2.70)

В приближении НДП

hp _{i® k, j® l} = d _ij d _kl (e _k - e _i) +å [2(1-R)сm _j сm _l cn _i сn _k - сm _j сm _i сn _k cn _l], (2.71)

где R=0 для синглетных состояний и R=1 – для триплетных.

Расчет проводится методом ССП, причем вначале определяют МО для основного состояния, а затем, используя их, строят волновые функции возбужденных состояний.

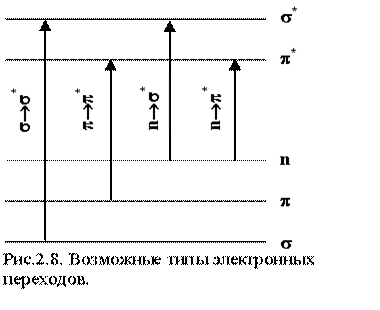
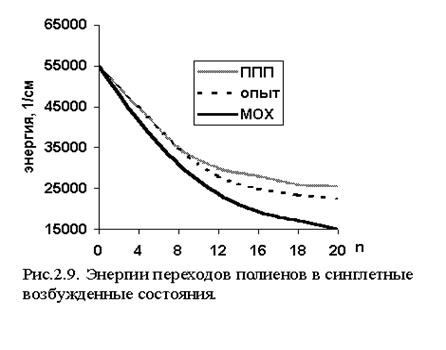
Метод Парризера-Попла-Парра включает в себя метод КВ и очень хорошо зарекомендовал себя как при определении геометрии, потенциалов ионизации и сродства к электрону, так и при расчетах оптических спектров поглощения сопряженных органических молекул. Спектр поглощения состоит из нескольких полос, связанных с определенными электронными переходами. Для плоских молекул МО можно разделить на три группы: s , p и n^* . Наболее вероятное относительное расположение соответствующих энергетических уровней и разрешенные правилами отбора типы электронных переходов показаны на рис. 2.8. Диагонализизация матрицы hp _{i® k, j® l} называемой матрицей конфигурационного взаимодействия, дает энергии спектральных переходов и веса возбужденных конфигураций а_{i® k}. Ориентированный на p -электроны, метод ППП хорошо описывает p -p ^* переходы (рис. 2.9.): точность оценки синглет-синглетных переходов составляет 0,1-0,2 эВ или 3-5% .

Интенсивность полосы поглощения f определяется квадратом дипольного момента перехода и равна f =Кn ï å å а_{i® k} cn _i сn _k xï ². Она оценивается методом ППП с ошибкой 40-50%.

Метод МО Хюккеля

Этот чрезвычайно простой не-ССП метод, первоначально предложенный для углеводородов (Хюккель, 1931), основан на нескольких очень сильных приближениях:

1) Принимается p -электронное приближение; считают, что АО образуют ортонормальный базис, т.е. Sm n = d m n .

2) Межэлектронными взаимодействиями (т.е. всеми двухэлектронными кулоновскими и обменными интегралами) пренебрегают. Из-за этого решение уравнений метода не требует итераций и проводится в один шаг.

1. Матричные элементы оператора Фока оцениваются на основании эмпирической информации и являются фиксированными:

hm m = a m ,

hm n = kb m n . (2. 72)

a m называется кулоновским интегралом (его не следует путать с двухэлектронными кулоновскими интегралами g _AB), он принимается равным потенциалу ионизации электрона на орбитали m в свободном атоме.

4) Принимается, что b m n =0, если АО m и n не принадлежат ковалентно связанным атомам.

Соответствующие этим приближениям уравнения Рутана имеют вид

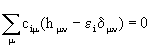(2.73)

и называются уравнениями Хюккеля, имеющими ненулевые решения при равенстве нулю детерминанта

ï hm n - e _{id m n} ï = 0. (2.74)

Полная энергия в этом методе есть просто сумма орбитальных энергий

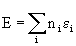, n=0, 1 или 2, (2.75)

где n – число электронов на МО.

Уравнения Хюккеля могут быть легко записаны и решены для любой системы. Рассмотрим пример молекулы этилена С₂Н₄, имеющей 2 p -электрона (свяжем их с c (р_z) -АО атомов углерода, направленными перпендикулярно плоскости молекулы). Интегралы a _С = -11,0 эВ, b _СС –2,4 эВ. Детерминант (2.74) имеет вид

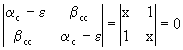(2.76)

(здесь введены обозначения х=(a _С - e )/b _СС). Раскрывая определитель, имеем:

х² –1=0 и х = ± 1, т.е. e ₁= a _С +b _СС , e ₂ =a _С - b _СС.

В принятых обозначениях система уравнений (2.73) имеет вид

с₁ х + с₂ = 0

с₁ + с₂ х = 0, (2.77)

Подставим теперь х = ± 1 в (2.77). При х= -1 имеем с₁ = с₂ . Используя условие нормировки волновой функции этилена с₁² + с₂² = 1, получаем с₁ = с₂ = 1/Ö 2 . Таким образом, одна из p -МО этилена имеет вид

j ₁ = 1/Ö 2 (c ₁ +c ₂). (2.78)

При х = 1 имеем с₁ = - с₂ и, повторяя рассуждения, получаем другую p -МО.

j ₂ = 1/Ö 2 (c ₁ - c ₂). (2.79)

Так как b _СС < 0, то e ₁ < e ₂ причем, e ₁ - e ₂ = 2b _СС. Это означает, что МО j ₁ более энергетически стабильна.

Полинг, Уэлланд, Стрейтвизер, Дьюар и другие предложили различные модификации метода Хюккеля, распространив его, в частности, на системы с гетероатомами в цикле. Модификация, в основном, касалась способа выбора параметров a и b и подробно описана в литературе (М. Дьюар. Метод молекулярных орбиталей в органической химии).

Метод Хюккеля, безусловно, является лишь качественным: он ограничен предсказанием энергетики МО сопряженных систем и не способен дать информацию о молекулярной структуре. Однако за счет удачной параметризации этот метод может давать хорошие относительные орбитальные энергии для рядов p -электронных органических и металлоорганических систем. Это позволяет, в частности, идентифицировать полосы в электронных спектрах поглощения таких молекул, отождествляя разности орбитальных энергий e _k - e _i с энергиями переходов.

Расширенный метод Хюккеля

Наиболее радикальная модификация метода Хюккеля принадлежит Р. Хоффману (1963). Он предложил сохранить оригинальную схему Хюккеля, но включить в рассмотрение все валентные (а не только p ) орбитали и явно учесть интегралы перекрывания. В итоге уравнения метода, получившего название расширенный метод Хюккеля (РМХ), формально совпадают с уравнениями Рутана (2.13), однако содержание матричных элементов совершенно иное. Матричные элементы оператора Фока Fm n º hm n являются параметрами или оцениваются с помощью соотношений, включающих эти параметры. Наиболее часто используются следующие оценки:

hm m = - Im . ,

hm n = 0.5K(hm m + hn n ). (2.80)

В варианте Вольфсберга-Гельмгольца К=1,75. Интегралы перекрывания вычисляются аналитически со ОСТ.

Энергия молекулы с закрытой оболочкой в методе РМХ является удвоенной суммой энергий занятых МО и описывается выражением

Е= 2( å å с²_im hm m + _{å å å} с_im с_in hm n ), (2.81)

в котором члены, ответственные за межэлектронное и межъядерное взаимодействие, не учитываются. В системах с равномерным распределением электронов выражение (2.81) дает хорошие относительные оценки энергии в рядах соединений. Гетероатомы нарушают равномерность электронного распределения и РМХ здесь часто непригоден. Тем не менее расширенный метод Хюккеля дает зачастую лучшие результаты, чем его простой аналог, при изучении конформаций циклических молекул, барьеров внутреннего вращения, относительный порядок уровней энергии.

Уместно отметить роль, которую РМХ сыграл в развитии химии. Именно с его помощью было установлен механизм связывания в металлоценах, сфомулировано правило Вудворда-Хоффмана, исследованы свойства основных состояний многих алифатических и ароматических систем и др.

Программа, реализующая расширенный метод Хюккеля имеется в Интернет: gopher: //infomeister.osc.edu:73/11/software/SOUR CES/FORTRAN/EHT

Таблица 3.1.

Характеристики основного состояния гомоядерных молекул

Молекула	Кратность связи Р	De, эВ	Re, Å	Молекула	Кратность связи Р	De, эВ	Re, Å
Н2+	1/2	2.8	1.06	С2	2	6.4	1.24
Н2	1	4.75	1.74	N2+	2 1/2	8.9	1.12
Не2+	1/2	3.0	1.08	N2	3	9.9	1.10
Не2	0	—	—	О2+	2 1/2	6.6	1.12
Li2	1	1.132	2.67	О2	2	5.2	1.21
Ве2	0	—	—	F2	1	1.4	1.42
В2	1	3.0	1.59	Ne2	0	-	-

Полная энергия молекулы не может служить критерием связывающих или разрыхляющих свойств МО: как те, так и другие уменьшают полную энергию молекулы.

Рассмотрим теперь электронные конфигурации некоторых гетероядерных молекул типа АВ, построенных из элементов первого и второго периодов.

Молекула LiH – простейшее гетероатомное соединение с энергией связи 242.4 кДж/моль, лежащей между энергиями Li₂ и H₂. Два ls электрона Li образуют несвязывающую МО, экранирущую ядро Li, тогда как 2s АО Li и 1s Н, перекрываясь, образуют связывающую s-МО s-типа, обеспечивающие ординарную связь. При этом ядро Н сильнее влияет на электронное распределение и электроны смещаются в молекуле к ядру Н. В результате молекула приобретает дипольный момент 5.9D. Такие связи с асимметричным распределением электронной плотности и дипольным моментом называются ионными (частично ионными) связями.

Молекула НF имеет конфигурацию (1s_F)²(2s_F)²(2p_F)²(2p_F)²(s_sН-2pxF)², причем только одна орбиталь s_sH-2pxF является молекулярной: остальные сохраняют свой атомный характер. Электроны несколько смещены к атому F (дипольный момент равен 1.8 D) и связь в НF – частично ионная ординарная.

Молекула LiF имеет конфигурацию (1s_Li)²(1s_F)²(2s_F)²(2p_F)²(2p_F)²(s_sLi-2pxF)², где только одна орбиталь s_sLi-2pxF - молекулярная. Электроны сильно смещены к атому F (дипольный момент равен 6,3 D) и связь в LiF – ионная ординарная.

В таблице 3.2 даны электронные конфигурации и характеристики некото-рых других гетероядерных молекул. На рис. 3.6 приведена схема уровней энергии валентных МО молекулы СО и пространственное распределение этих МО.

Таблица 3.2.

Электронные конфигурации и характеристики некоторых гетероядерных молекул.

Молекула	Конфигурация валентных МО	Длина cвязи, Å	Кратность связи	Энергия связи, кДж/моль
CN	(p 2рy)2(p 2рz)2(s 2рx)1	1.18	2 1/2	785.8
CO	(p 2рy)2(p 2рz)2(s 2рx)2	1.13	3	1070.1
NO	(p 2рy)2(p 2рz)2(s 2рx)2(p *2р)	1.15	2 1/2	677.2

 

Топологическая теория

Иной подход к анализу химической связи дает топологическая теория молекулярной и кристаллической структуры, разработанная Бейдером. Этот подход, в отличие от концепции деформационной ЭП и ее разновидностей, имеет существенное преимущество: получаемые результаты не зависят от используемой модели промолекулы.

Положения топологической теории, существенные для рассматриваемых вопросов, следующие. Структура многоэлектронной системы при ядерной конфигурации R полностью определяется набором и сортами критических точек ЭП r (r,R), точек r_c, где градиент ЭП Ñ r (r,R) равен нулю. Вторые производные ЭП, вычисленные в этих точках, составляют действительную симметричную матрицу размером 3´ 3 (гессиан). Главные компоненты кривизны ЭП в точке r_c (собственные значения гессиана l _i) определяют ранг р и признак q критической точки {p,q}; ранг есть число ненулевых собственных значений, признак-алгебраическая сумма их знаков. Возможны всего четыре невырожденные критические точки ЭП: (3, -3), (3, -1), (3, 1), (3, 3).

Критические точки (3, -3) отвечают локальным максимумам ЭП, которые совпадают с положениями ядер. Интегральные кривые r(s)=r_o+ ò Ñ r [r(t),R]dt (градиентные траектории) составляют набор решений дифференциального уравнения dr(s)/ds=ò Ñ r [r(t),R] при начальном условии r(0)= r₀. Все траектории, которые заканчиваются на некотором ядре, определяют область пространства химической системы, которая называется бассейном этого ядра. Совокупность ядра и ЭП в пределах его бассейна определяет атом в химической системе. Последняя оказывается разделенной на бассейны, каждый из которых содержит только одно ядро. Каждая пара смежных бассейнов разделяется межатомной поверхностью S(r), поток вектора Ñ r через которую равен нулю:

Ñ _ρ(r) ∙ n(r) = 0, "r 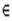S(r). (3.13)

Здесь n(r)-единичный вектор, нормальный к поверхности в точке r. Благодаря условию (3.13), любая межатомная поверхность образуется градиентными траекториями, которые заканчиваются в критической точке связи (3, -1), лежащей на этой же поверхности. Ее положение обозначается r_b. Собственный вектор гессиана, отвечающий положительной кривизне в точке r_b, задает исходные направления двух градиентных траекторий, которые заканчиваются в двух соседних ядрах. Они определяют линию связи: вдоль этой линии ЭП максимальна по отношению к любым малым боковым смещениям. Существование линии связи является необходимым и достаточным условием образования связи между атомами.

Собственные векторы, отвечающие двум положительным собственным значениям гессиана, вычисленным в критической точке (3,1), генерируют поверхность, на которой ЭП минимальна именно в этой точке. Такая ситуация реализуется в циклических молекулах, поэтому точка (3,1) называется циклической критической точкой. Точка (3,3) соответствует локальному минимуму ЭП: собственные векторы, отвечающие трем его положительным собственным значениям, порождают бесконечное число градиентных траекторий, заключенных в области пространства, ограниченной несколькими циклами; это имеет место в клеточных молекулах.

Плоская циклическая молекула S₂N₂ (рис. 3.12) является примером системы, в которой реализуются все типы критических точек, кроме точки (3,3). Критические точки связи лежат на линиях S-N, которые таким образом являются связанными, однако на линиях S-S и N-N таких точек нет. В центре цикла ЭП минимальна, здесь находится критическая точка (3,1) и это единственное место, где соприкасаются бассейны пары атомов S и пары атомов N, химическая связь между которыми отсутствует. На рис. 3.12 хорошо видно, что у атома с большей электроотрицательностью расстояние от ядра до критической точки (3, -1) вдоль линии связи больше. Таким образом, размер бассейна и электроотрицательность атома коррелируют. Установлено, что значение ЭП в критической точке (3, -1) коррелирует с длиной линии связи L (которая в общем случае не совпадает с длиной межъядерного вектора) и с порядком связи по Льюису п. Эти зависимости имеют вид:

r(r_b)=aL+b,

n=exp{A[ρ(r_b)–B ]} (3.14)

(величины коэффициентов а, в, А и В зависят от базиса, в котором рассчитана ЭП и от сорта связанных атомов) и для связей углерод-углерод приведены на рис. 3.13 и 3.14.

ЭП s - и p -орбиталей пространственно не разделяются и критические точки (3, -1) наблюдаются как на простых, так и на кратных связях. Однако форма распределения ЭП в поперечном сечении для этих связей различается; соответственно различается здесь и кривизна ЭП в разных направлениях. Для оценки ассимметрии распределения ЭП в этой плоскости, проявляющейся на картах d r в виде удлинения избыточного пика, в топологической теории используется параметр эллиптичности:

ε = λ₁/λ₂ – 1, | λ₁|>| λ₂|. (3.15)

ЭП быстрее уменьшается вдоль направления наибольшей кривизны. Если пренебречь взаимным влиянием связей и межмолекулярным взаимодействием, то можно ожидать для ординарных связей l ₁=l ₂ и e =0. Если для кратных связей e отлично от нуля, то этот параметр дает оценку p -характера связи. Например, в молекуле S₂N₂ e (S-N) =0,572 (расчет в базисе 6-21G*). Однако наличие двух указанных факторов приводит к e >0 для формально ординарных связей, например для связи С-О в молекуле a -щавелевой кислоты, в которой существенны эффекты сопряжения, и связи С-С в кристалле этана, где проявляется воздействие ближайших соседей. Таким образом, адекватная интерпретация причин ненулевой эллиптичности связи требует учета многих обстоятельств.

Ценную химическую информацию содержит лапласиан ЭП Ñ ^2r . Если ЭП в данной точке превышает среднее значение ЭП в соседних точках, то Ñ ^2r <0; в противном случае Ñ ^2r >0. Разница между локальным значением и средним в ближайшей окрестности максимальна в критических точках ЭП. Таким образом, электроны концентрируются в регионах, где Ñ ^2r <0 и деконцентрируется там, где Ñ ^2r >0. Как видно из рис. 3.12, г, отрицательные значения Ñ ^2r проявляются в межъядерном пространстве вдоль линии ковалентной связи S-N, где наличествует малая положительная кривизна ЭП вдоль этой линии и большая отрицательная кривизна в других направлениях, а также в области неподеленных электронных пар атомов N.

Лапласиан ЭП прямо связан с локальными вкладами в электронную энергию молекулы и кристалла плотностей кинетической g(r) и потенциальной v(r) энергий:

(ħ²/4m)Ñ ²ρ(r) = 2G(r) +V(r). (3.16)

Поскольку g>0, a v<0, то в областях, где происходит концентрация электронов, плотность потенциальной энергии выше.

Важной характеристикой является значение лапласиана ЭП в критической точке связи. Оно определяется соотношением между отрицательными и положительными собственными значениями гессиана l ₁, l ₂ и l ₃, и, таким образом, зависит от характера химической связи. Эта характеристика позволяет естественным образом разделить все атомные взаимодействия на два класса, в зависимости от распределения ЭП между ядрами. Если для ЭП здесь характерно доминирование отрицательной кривизны, то это означает, что ЭП концентрируется вокруг критической точки (3-1) и взаимодействие атомов можно отнести к ковалентному типу. Потенциальная энергия электронов в области, окружающей точку r_b, по меньшей мере, в два раза будет превосходить кинетическую энергию. Если же положительная кривизна ЭП доминирует в точке r_b, то ЭП оказывается смещенной к каждому из взаимодействующих атомов и сконцентрированной в атомных бассейнах. Это отражает действие принципа Паули. Такие атомные взаимодействия считаются взаимодействиями ионного типа. В области, окружающей критическую точку связи, доминирует кинетическая энергия, а области, где доминирует потенциальная энергия, оказываются пространственно-разделенными. Конечно, приведенное разделение носит очень грубый характер, а названия взаимодействий не отражают реального многообразия их проявлений. Тем не менее, как видно из табл. 3.3 и 3.4, где приведены расчетные данные, это разделение охватывает большинство разновидностей химических связей.

Таблица 3.3. Характеристики атомных взаимодействий в терминах локальных свойств электронной плотности

Таблица 3.4. Топологические и энергетические характеристики ковалентных связей в терминах локальных свойств электронной и энергетической плотности

Введем понятие плотности локальной электронной энергии:

Н_е(r) = G(r) + V(r) (3.17)

Знак Н_е однозначно показывает, что кинетическая или потенциальная энергия доминирует в той или иной точке пространства. Если в межъядерной области доминирует V(r), то это свидетельствует, что аккумуляция электронов здесь является стабилизирующей. В противном случае распределение ЭП в межъядерной области дестабилизирует систему. Таким образом, локальная энергия электронов Н_е служит важной характеристикой связывания в многоэлектронных системах.

Эмпирический материал, собранный в табл. 3.3 и 3.4, позволил сформулировать признаки наличия ковалентной химической связи между парой атомов. Связь образуется, если:

1) между атомами существует критическая точка (3, -1) (необходимое условие);

2) плотность локальной электронной энергии Н_е в этой точке отрицательна (достаточное условие).

Дать аналогичные определения ионной, водородной и ван-дер-ваальсовой связям, отделяя их друг от друга, не удается. Для этих связей характерны положительные значения плотности локальной электронной энергии в критической точке связи, поэтому в рамках топологического анализа их приходится объединять под общим названием взаимодействий ионного типа.

Химической связи

Гамильтониан многоэлектронной многоядерной системы в пренебрежении релятивистскими эффектами состоит из членов, описывающих кинетические и потенциальные энергии электронов и ядер. Сложились два подхода к описанию взаимодействий в таких системах – электростатический или силовой (binding) и энергетический (bonding). Силы, действующие в таких системах, подчиняются закону Кулона, причем межэлектронные взаимодействия происходят таким образом, чтобы удовлетворялся принцип Паули. Влияние магнитных сил, обусловленных наличием электронного и ядерного спинов, на полную энергию пренебрежимо мало, не говоря уже о гравитационных силах.

Электростатический подход ищет объяснение химической связи в терминах сил, действующих в молекулах. В энергетическом подходе для этого анализируют изменения кинетической и потенциальной энергий. Оба подхода являются взаимодополняющими и во многом опираются на две следующих важных теоремы.

Теорема вириала устанавливает соотношение между полной энергией многоэлектронной и ее кинетической и потенциальной компонентами. Можно показать, что плотности кинетической g(r) и потенциальной v(r) энергий и электронная плотность r (r) в системе с произвольной ядерной конфигурацией связаны соотношением:

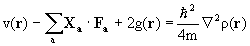(3.18)

Здесь полная плотность потенциальной энергии v(r)=v_NN(R)+ v_Ne(R, r) +v_ee(r), R_a –координата ядра а, R=(x, y, z), F_a – сила (вектор), действующая на это ядро. Величина 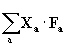называется вириалом сил, действующих на ядра системы. Если система находится в равновесии, силы, действующие на ядра, равны нулю. Под понятием “вирал” имеют ввиду сумма произведений векторов сил на вектора направлений их действия. Сам вириал – величина скалярная и измеряется в единицах энергии.

Интегрируя оставшиеся члены в (3.18) по всему пространству, легко получить следующее соотношение для средних значений компонент полной энергии:

V + 2G =0 или -V = 2G (3.19)

(использована теорема Остроградского-Гаусса, согласно которой объемный интеграл от Ñ ^2r (r) по всему пространству равен нулю). Полная энергия системы равна сумме потенциальной и кинетической энергии Е=G+V, отсюда следует соотношение:

Е = - G. (3.20)

Соотношения (3.19) и (3.20) выражают содержание теоремы вириала, характеризует систему в состоянии равновесия. Они справедливы как для полной системы, так и для частей, из которых она образуется; для молекул и атомов. Именно поэтому они полезны при анализе природы химической связи.

Рассмотрим с этих позиций образование молекулы. Для бесконечно удаленных атомов (состояние 1) и для стабильной молекулы (состояние 2) выполняются соотношения:

G₁= -(1/2)V₁ , G₂= -(1/2)V₂ . (3.21)

Изменение компонент энергии при образовании молекулы (при абсолютном нуле) равно:

D G = -(1/2) D V. (3.22)

Соответствующее изменение полной энергии

D Е= D G +D V (3.23)

можно связать, используя теорему вириала, с изменением кинетической и потенциальной энергий:

D Е=D G+D V = -(1/2)D V+D V = (1/2)D V,

D Е=D G+D V = D G - 2D G = -D G. (3.24)

Отсюда видно, что изменение полной энергии имеет тот же знак, что и изменение потенциальной энергии. Поскольку при образовании молекулы полная энергия понижается, то это сопровождается понижением потенциальной энергии. Одновременно кинетическая энергия повышается, но ее эквивалентное изменение вдвое меньше по величине (G > 0!). Таков общий баланс изменений энергии, сопровождающих образование молекулы. На этом фундаменте должен строиться дальнейший детальный анализ.

Теорема Гельмана-Фейнмана гласит, что для точной и хартри-фоковской волновой функции справедливо соотношение

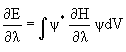, (3.25)

где l - некоторый параметр, от которого зависит энергия.

Примение соотношения (3.25) к изучению сил, действующих в молекуле (Гельман, 1936, Фейнман, 1939) известно под названием электростатическая теорема. В качестве параметра используются ядерные координаты: l =R_а. Кинетическая энергия электронов и межэлектронное взаимодействие от координат ядер зависят не явно. Поэтому в этом случае (3.25) дает для ядра а молекулы:

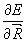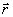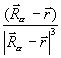=Z_a ρ_{( ) dV + 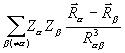,} (3.26)

где ρ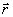_{( )} = Ψ*Ψ – электронная плотность.

Производная 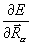описывает силу, действующую на ядро в молекуле. Ее компонента по одной из осей координат равна

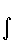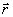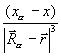F_xα = – Z_α ρ_{( )} dV + 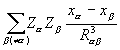. (3.27)

Можно заключить, что силу, действующую на ядро а, можно рассматривать классически как сумму электростатического взаимодействия ядра а с электронной плотностью r и с другими ядрами. Поэтому теорему Гельмана-Фейнмана, записанную в форме (3.26), называют также электростатической теоремой.

Из сказанного следует интересный и важный вывод. В классической электростатике показано, что статическая система электрических зарядов не может быть в равновесии (теорема Ирншоу). Тем не менее, если энергия стационарна и получена с помощью вариационного принципа, то ее значение вычисленное как среднее от гамильтониана (как требует квантовая механика) и таковое, вычисленное интегрированием сил, действующих на ядра, по мере их сближения из бесконечности в равновесное положение (т.е. классически), эквивалентны. Это означает, что квантовохимически “правильная” электронная плотность, отвечающая минимуму энергии, в принципе, позволяет получить корректное значение энергии классически с помощью соотношения:

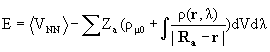(3.28)

(l ₀ характеризует значение, ниже которого система перестает быть стабильной).

В равновесных системах силы, действующие на ядра, равны нулю и анализируя соответствующее электронное распределение, можно выявить некоторые черты химической связи (Берлин, 1951). Рассмотрим применение силового подхода к двухатомным молекулам. Введем величину

f (r) = 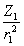cosθ₁ + 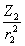cosθ₂ , (3.29)

являющуюся проекцией на межъядерную ось полной кулоновской силы, действующей в точке г на ядра с зарядами Z_i со стороны единичного отрицательного заряда. q - угол между направлением кулоновской силы, действующей на ядро 1 или 2 и межъядерной осью. С помощью этой величины силу F(R), действующую на ядра, разделенные расстоянием R, можно записать через ЭП в виде:

F(R) = 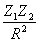- ƒ(r)ρ(r)dV (3.30)

В равновесии R=R_e и F(R_e)=0. Если принять, что r (г)>0 (отвлекшись от того, что эта функция описывает распределение отрицательного заряда), то знак вклада в значение силы F(R) в каждой точке г определяется знаком проекции полной силы f(r) в этой точке. Отрицательный заряд в областях, где f(r)>0, уменьшает значение F (“связывает” ядра), а в областях, где f(r)<0, увеличивает значение F. Области, в которых f(r)>0 и f(r)<0, называются связывающими и антисвязывающими, соответственно.

В итоге, пространство молекулы можно разделить на связывающую область, в которой ЭП создает электростатические силы, действующие на ядра по направлению друг к другу, и на антисвязывающую область, в которой силы, действующие на ядра, стремятся их раздвинуть. Граничная поверхность, разделяющая связывающую и антисвязывающую области, определяется условием

F_xa=F_xb (3.31)

Для гомоядерной двухатомной молекулы эта поверхность имеет вид двухплоскостного гиперболоида. Области связывания и антисвязывания на плоскости для некоторых молекул показаны на рис.3.15 и 3.16.

Взаимодействие пары атомов сопровождается индуцированием на каждом из них дипольного момента; электронные плотности атомов при этом несколько смещаются друг к другу. Очевидно, что для стабильности системы необходимо, чтобы ЭП в связывающей области при R=R_e создавала силы, компенсирующие отталкивание ядер и действие на ядра ЭП в антисвязывающих областях. Исследуем этот вопрос. В большинстве случаев, показанных на рис. 3.8-3.11, образование химической связи сопровождается накоплением ЭП в пространстве между ядрами, которое и отождествляется со связывающей областью: электронный заряд в этом районе стремится приблизить ядра друг к другу. Электроны, находящиеся вне межъядерной области, наоборот стремятся удалить ядра друг от друга, поэтому эти области часто определяют как антисвязывающие. На основании этих аргументов ранее считалось, что требование d r >0 в связывающей области является необходимым (но недостаточным) для образования стабильной системы. Однако имеются примеры таких реально существующих систем, как молекула F₂ , для которых характерно наличие минимумов d r в межъядерном пространстве. Можно привести и обратный пример. Вид стандартной карты d r для неустойчивой молекулы Ве₂ топографически аналогичен картам для стабильных двухатомных молекул, таких как 0₂ или N₂.

Помимо этого, можно считать твердо установленным, что в некоторых двухъядерных молекулах d r >0 не только в межъядерном пространстве: максимумы d r концентрируются, например, за ядрами. Другими словами, при образовании системы из атомов электроны перетекают и в несвязывающую (с точки зрения силового подхода) область. Такое перераспределение ЭП для двухатомных молекул подтверждается и экспериментальными данными по дифракции электронов на молекулах в газовой фазе.

Таким образом, возникновение стабильной системы обеспечивается весьма тонким балансом сил, действующих на ядра, и соответствующим перераспределением ЭП. Анализ этих сил с позиции перераспределения ЭП, происходящего при образовании химической связи, выявил следующее. Силу, действующую на ядро в двухатомной молекуле, можно записать через ЭП промолекулы r _пром и деформационную ЭП d r в виде

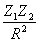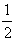
F(R) = - 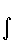ƒ(r)ρ_пром(r)dV –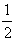 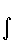ƒ(r)δρ(r)dV . (3.32)

Поскольку функция r _пром знакопостоянна (положительна с учетом ранее принятого знака для r ) во всем пространстве, а d r — знакопеременная функция, совпадение областей, в которых f и d r имеют одинаковые знаки, должно способствовать стабилизации системы. По этой причине, в частности, области d r <0 в антисвязывающей в силовом смысле области за атомными ядрами на самом деле отвечают связыванию. И, действительно, на картах d r многих молекул имеются минимумы за ядрами на продолжениях линий связи (см., например, рис. 3. 9 - 3.11).

Проанализируем различие в природе связывания в молекулах N₂ и F₂. В первой из них (рис. 3.8) на карте стандартной d r наблюдается существенная концентрация избыточной ЭП вблизи межъядерной оси и на ее продолжении за ядрами. Во второй молекуле (рис. 3.8) имеются минимумы d r между и позади ядер. Это приводит к различиям в подынтегральных выражениях в последнем члене в выражении (3.27), которые иллюстрирует рис. 3.17. В N₂ основной вклад в положительное значение интеграла ò f(r)d r (r)dV, отвечающее связыванию, вносит связывающая область между ядрами, где f(r)>0 и d r (r)>0. Наоборот, в молекуле F₂ основное значение этого интеграла определяется областями позади ядер и областями, тороидально охватывающими линию связи вблизи ядер, где f(r) <0 и d r (г)<0. В обеих молекулах важное значение имеют деформации ЭП вблизи атомных ядер, где их характер совершенно различен. Отсюда ясно, что при анализе химической связи нужно рассматривать не только межъядерное пространство, но и распределение ЭП во всех областях исследуемой системы.

Недостатком анализа, основанного на выражении (3.27), является использование не подчиняющихся вариационному принципу функций r _пром и d r , поэтому вычисляемые с их помощью компоненты силы могут оказаться физически бессмысленными. В связи с этим иногда целезообразно рассчитывать функции (3.27) для отдельных молекулярных орбиталей: это позволяет соотнести их со связывающими, несвязывающими и антисвязывающими МО. Соответствующие силы имеют в этом случае ясный смысл.

Другой существенный дефект силового подхода в том, что если явно учесть, что ЭП системы r везде отрицательна (а не положительна, как это предполагалось выше), то связывающие и антисвязывающие области следует поменять местами, поскольку заряд ядер остается строго положительным.

Укажем, что силовой подход непригоден для рассмотрения метастабильных состояний, энергия которых выше энергии отдельных атомов: ведь значение силы, действующей на ядро, и в этом случае может быть равным нулю. На вершине энергетического барьера химической реакции, разделяющего исходные и конечные продукты, сила также равна нулю.

Концепция силового связывания не может исчерпывающим образом объяснить возникновение или отсутствие химической связи, поскольку она не позволяет сделать какие-либо выводы относительно изменения кинетической энергии при образовании связи. Перераспределение ЭП, однако, происходит таким образом, что минимизируется полная энергия. Чтобы описать этот процесс, необходимо привлечение иного, энергетического, подхода к анализу природы химической связи.

Первый обстоятельный энергетический анализ, касающийся природы ковалентной связи, принадлежит Рюденбергу, рассматривавшему молекулу Н₂ и ион Н₂⁺. Его выводы кратко могут быть суммированы следующим образом. Конструктивная интерференция атомных волновых функций при уменьшении расстояния между атомами приводит к уменьшению кинетической энергии электронов относительно отдельных атомов вследствие уменьшения градиента соответствующих орбиталей. Электронный заряд при этом смещается из областей близ ядер, где потенциал низок, в межъядерное пространство (см. рис. 3.7), увеличивая потенциальную энергию системы. Одновременно ЭП в непосредственной близости от ядер возрастает, в результате чего кинетическая энергия соответствующих электронов увеличивается, а потенциальная - уменьшается. Суммарная энергия системы оказывается ниже, чем у совокупности исходных атомов, причем общий выигрыш в энергии обусловлен понижением кинетической энергии вследствие химического взаимодействия.

Последний вывод, однако, не согласуется с требованием теоремы вириала, согласно которой при образовании стабильной системы из атомов изменение кинетической энергии в среднем положительно, а потенциальной - отрицательно.

Распределение плотностей кинетической и потенциальной энергий электронов в общем случае имеет более сложный характер. Изучая этот вопрос, Бейдер обнаружил, что плотность кинетической энергии при ортогональном преобразовании базиса молекулярных орбиталей ( при переходе к базису естественных орбиталей, в котором матрица плотности диагональна ) имеет вид:

T(r) = - 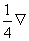²ρ(r)+G(r). (3.33)

Здесь G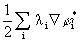(r)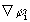= (r)∙ (r)= [ 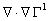(r, r′)]_r=r′= ,

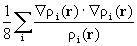ρ_i(r)=λ_i (r) (r), (3.34)

l _i - числа заселенности естественных орбиталей. Величина g(r) есть квазиклассическая положительная плотность кинетической энергии, фигурирующая в теореме вириала (3.18). Второй член в (3.33) описывает квантовомеханический вклад в полную плотность кинетической энергии t(r): он имеет разный знак в разных областях пространства. Как мы теперь видим, в теорему вириала (3.18) входят оба эти кинетических члена. Интеграл от (h ²/4m)Ñ ^2r (r) по всему пространству равен нулю, поэтому среднее значение кинетической энергии Т равно среднему значению g, обозначаемому как G.

Для анализа компонент энергии связи введем параллельную

T₁= 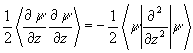(3.35)

и перпендикулярную

T 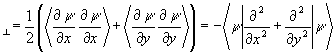(3.36)

составляющие средней кинетической энергии. Для сферического (изолированного) атома Тô ô = (1/2)Т^ и d =(T^ - Tç ç )/Т = 1/3. Для связанных систем отклонение индекса деформации s от атомного значения 1/3 может служить мерой изменений компонент кинетической энергии, произошедших при образовании химической связи.

Как видно из выражения (3.34), для одноэлектронной молекулы H₂⁺, кинетическая энергия полностью определяется градиентом ЭП Ñ r . Однако уже для двухэлектронной молекулы Н₂ разложение по естественным орбиталям дает лишь 98% полной ЭП и её кинетическая энергия только приближенно определяется Ñ r . Из-за накопления ЭП между ядрами в молекуле H₂ компонента Ñ r , параллельная линии связи, мала, величина g(r) в этом районе уменьшается по мере продвижения от ядер к центру связи (рис. 3.16); соответственно уменьшается и вклад в Т параллельного линии связи градиента ЭП. Перпендикулярная составляющая градиента ЭП здесь намного больше параллельной из-за сжатия ЭП по направлению к линии связи. За ядрами обе компоненты Ñ r дают большой вклад в g(r), так как ЭП здесь увеличивается примерно одинаково при приближении к ядру. Изменение G(r) по отношению к отдельным атомам между ядрами отрицательно. Такое поведение компонент плотности кинетической энергии отражается и на их средних значениях. В равновесной молекуле H₂ Tç ç (R_e)<(1/2)T^ (R_e), тогда как Tç ç (R_e)<(1/2)Tç ç (¥ ) и T^ (R_e)<(1/2)T^ (¥ ). Индекс деформации s =0.4740, т.е. в молекуле Н₂ он больше атомного значения 1/3. Примечательно, что наименьшее значение Tç ç отвечает в Н₂ не равновесному расстоянию (1.4 а.е.), а значению 2.0 а.е. Тем не менее, и при равновесном состоянии Tç ç =0.3043 а.е., т. е. меньше атомного значения 0.3333 а.е. Однако при R<2.0 a.е. начинает заметно возрастать величина T^ . Поэтому в стабильной молекуле Н₂ кинетическая энергия будет увеличиваться за счет увеличение G^ , а в силу теоремы вириала это повлечет за собой уменьшение потенциальной энергии. Рюденберг же рассматривал только составляющую кинетической энергии, параллельную линии связи, и его выводы, следовательно, неполны.

Как впоследствии оказалось, анализ, основанный на двух специфических системах - молекулах Н₂ и Н₂⁺,-, вообще нельзя перенести на другие, более сложные системы. В этих молекулах в основном состоянии электроны занимают только связывающие МО, не имеющие узлов, в них нет p -связей, неподеленных пар и т.д. Поэтому рассмотрим несколько более общих случаев.

В нестабильной системе Не₂ электронами заняты связывающая и разрыхляющая МО и деформационная ЭП в пространстве между ядрами, отражая действие принципа Паули, отрицательна. В этой области как gê ê (r), так и g^ (r), а значит и Tç ç и T^ увеличены по сравнению с атомными значениями, причем Tç ç увеличивается при сближении атомов несколько сильнее, чем T^ . Из-за этого индекс деформации при R=2.0 а.е. Равен d =0.290, т. е. меньше атомного значения 1/3, и плотность кинетической энергии в межъядерном пространстве Не₂ систематически выше, чем у отдельных атомов. Таким образом, в Не₂ нет, как в Н₂, областей пространства, где аккумуляция ЭП пони жает потенциальную энергию и одновременно дает низкую кинетическую энергию.

Молекула N₂ дает пример многоэлектронной системы общего вида, где g(r) нельзя и приближенно связать с Ñ r (r), поскольку сумма орбитальных градиентов плотности не сводится к градиенту их суммы. Распределение g(r) в межъядерном пространстве определяется как связывающими, так и разрыхляющими МО, занятыми электронами (рис. 3.19). Наличие узловых поверхностей у разрыхляющих s -МО в центре межъядерного расстояния приводит здесь к заметному вкладу их градиента в компоненту плотности кинетической энергии, параллельную линию связи. p -МО также дает вклад в gê ê (r). Таким образом, размягчение Ñ r в таких системах еще не означает малости компоненты плотности кинетической энергии gê ê (r).

Профиль разности d g(r)= g(r)_мол -å g_атом(r) показывает, что d g в центре межъядерного пространства, где в N₂ аккумулируются электроны, увеличивается по сравнению с отдельными атомами. В окрестностях ядер картина распределения d g сложнее: плотность кинетической энергии оказывается отрицательной как в области уменьшения ЭП, со стороны связывающей (в силовом подходе) области, так и в областях концентрации ЭП позади ядер, т. е. в антисвязывающих областях, отождествляемых с положением неподеленных электронных пар атомов N. Таким образом, концентрация электронов вдоль оси двухатомной молекулы в антисвязывающих областях понижает кинетическую энергию относительно отдельных атомов. Интересно, что такое сложное распределение плотности кинетической энергии приводит в итоге к тому, что в молекуле N₂ индекс деформации d =0.3331, т. е. он практически не отличается от атомного значения.

Таким образом, кинетическая энергия в многоэлектронных системах распределена совершенно иначе, нежели в молекуле Н₂. Размягчение градиента ЭП вдоль линии связи не является существенным фактором при образовании связи. Следовательно, молекула Н₂ не может служить образцом при изучении природы химической связи. Более того, как видно из приведенных выше выражений, плотность кинетической энергии g(r) зависит не только от градиентов естественных орбиталей, но и от лапласиана ЭП. В некоторой точке пространства знаки Ñ ^2r (r) и g(r) могут как совпадать, так и отличаться, причем знак g(r) зависит от знака произведения Ñ j ∙Ñ j *. Для образования химической связи необходима благоприятная контраградиентность орбиталей, описывающих связь.

Для анализа причин возникновения химической связи необходимо рассматривать не только центральные области вдоль межъядерных векторов, но и ЭП вблизи ядер. ЭП именно в этих областях в основном определяет величины сил, действующих на ядра, а общая картина d r отражает изменения полной ЭП, приводящие к обсуждавшимся выше изменениям энергии. Рюденберг высказал мнение, что вблизи ядер происходит сжатие ЭП, увеличивающее кинетическую энергию электронов в этой области. Однако позже было установлено, что такое сжатие характерно лишь для молекулы Н₂. В общем же случае, в молекулах, состоящих из легких атомов от Н до F, s -плотность атомных остовов поляризуется в направлении, противоположном дипольной деформации валентных электронных оболочек. В таких молекулах результирующее действие электростатических сил, порождаемых p -МО, почти равно нулю. В согласии с этим выводом именно такое распределение ЭП найдено у s -МО молекулы N₂ (рис. 3.20).

Силы, действующие на ядра, сильно зависят от числа валентных электронов во взаимодействующих атомах и соответственно от характеристик волновых функций, описывающих эти электроны: главного, орбитального и магнитного квантовых чисел. Именно эти характеристики во многом определяют особенности распределения d r , которые обычно и пытаются соотнести с характером химической связи. При взаимодействии атомов, имеющих 3s- и Зр-электроны во внешней оболочке, конструктивная интерференция в области s -связи будет более слабой, чем атомов второго периода таблицы Менделеева. Причина этого кроется в большом числе узлов у радиальных волновых функций у первых из них. В то же время, p -взаимодействие атомов в обоих случаях не должно существенно отличаться. Причем, если в системе есть занятые электронами p -орбитали, то они, в основном обеспечивают связывание, поскольку влияние s -орбиталей в значительной степени взаимно компенсируется.

В таблице 3.5 приведены значения компонент gê ê (r_с) и g^ (r_с) в критических точках (3, -1) в молекулах с разными типами химической связи. Отношение этих величин отражает отношение компонент кривизны ЭП в критической точке связи. Оказалось, что для атомных взаимодействий ковалентного типа gê ê (r_с) < g^ (r_с), тогда как для взаимодействий ионного типа gê ê (r_с) > g^ (r_с). Кроме того, плотность кинетической энергий, приходящаяся в критической точке (3, - 1) на единицу электронного заряда, g(r_с)/ r (r_с)>1 для взаимодействий ионного типа и g(r_с)/ r (r_с)<1 для взаимодействий ковалентного типа. Это означает, что если положительная кривизна ЭП велика в результате сжатия ЭП к ядрам, то величина g(r_с)/ r (r_с) также достаточна велика, причем величина ее компоненты, параллельной линии связи, превышает величину перпендикулярной компоненты. Для ковалентных взаимодействий наблюдается обратная картина и отношение g(r_с)/ r (r_с) мало. Значение g(r_с)/ r (r_с) для молекулы H₂ аномально мало: эта молекула нетипична и в этом случае.

Интересное поведение демонстрирует плотность кинетической энергии молекулы F₂. В критической точке связи Ñ ^2r (r_с)= 0.233, l ₁=l ₂=-0.731, l ₃=1.694 а.е. Отношение g(r_с)/ r (r_с) равно 0.86, как и в молекуле N₂, однако g^ (r_с)/gê ê (r_с)= 0.751, что значительно меньше, чем в случае атомных взаимодействий ковалентного типа.

Резюмируя, следует подчеркнуть, что электростатические эффекты можно считать первопричиной образования химической связи из-за связывающих сил, действующих на ядра в промолекуле. Однако конкретный тип образующейся химической связи, определяемый сортом и числом взаимодействующих атомов, формируется под контролем принципа Паули в результате квантовомеханической интерференции электронных атомных облаков, которая может носить как конструктивный, так и деструктивный характер. Результирующее распределение ЭП отражает совокупность этих факторов и определяет энергетические особенности образовавшейся химической связи. Именно поэтому характеристики ЭП используются для идентификации химических связей.

Многоатомные молекулы

Молекулы, образованные из нескольких атомов, характеризуются, в общем случае, нелинейной и неплоской ядерной конфигурацией. МО этих молекул представляют собой делокализованные одноэлектронные функции, построенные из АО разных атомов (канонические МО). Эти функции не позволяют объяснить строение молекул, трансферабельность и аддитивность свойств функциональных групп. Чтобы проанализировать структуру и химическую связь в таких молекулах, существует ряд полуколичественных или качественных понятий. Рассмотрим основные из них.

Таблица 3.6.

Гибридные орбитали для разных случаев строения молекул

Гибридная орбиталь	Форма молекулы	пример
sp	Линейная	ВеН2
sp2	Плоская тригональная	BCl3
sp3	Тетраэдрическая	CH4
dsp2	Плоский квадрат	K2PtCl4
d2sp3	Октаэдрическая	SF6
dsp3	Тригональная бипирамида	PCl5
d4sp3	Додекаэдр	K4Mo(CN)8

Таблица 3.7.

Конфигурация связей центрального атома А в зависимости от числа электронных пар q на его валентных орбиталях

q	Конфигурация		q	Конфигурация
2		Линейная или уголковая	8	Квадратная антипризма
3		Равносторонний треугольник	9	Треугольная призма с тремя дополнительными вершинами
4		Тетраэдр
5		Тригональная бипирамида, квадратная пирамида	10	Квадратная антипризма с двумя дополнительными вершинами
6		Октаэдр	11	Икосаэдр без одной вершины
7		Октаэдр с дополнительной вершиной
			12	Икосаэдр

Таблица 3.8. Геометрия структуры молекул типа АХ_mЕ_n без кратных связей в файле cb_t3_8

Существуют простые правила, делающие модель Гиллеспи весьма эффективной.

а) Неподеленная электронная пара занимает больший объем, чем связывающая пара ординарной связи.

б) Сила отталкивания электронных пар в данной валентной оболочке понижается в следующем порядке: Е-Е, Е-Х, Х-Х (Е-неподеленная электронная пара, Х- связывающая электронная пара).

в) Объем связывающей электронной пары уменьшается с увеличением электроотрицательности лиганда.

г) Электронные пары двойной или тройной связей занимают больший объем, чем электронная пара ординарной связи.

Модель отталкивания электронных пар дает приближенный качественный метод предсказания структуры молекул. В последние годы эта модель нашла обоснование в топологической теории электронной плотности.

Таблица 3.9.

Основные координационные полиэдры в комплексных

соединениях переходных металлов с КЧ центрального атома 2—8

КЧ	Конфигурация связей центрального атома	Тип гибридизации	Пример структуры
2	Линейная	sp, dp	[Ag(NH3)2]+; ZnCo2(CO)8
	Угловая	Ds
3	Треугольная	sp2, ds2. dp2	Fe[N(SiMe3)2]3; Ni(CO)3
	Пирамидальная	d2p	Мо(СО)з
4	Тетраэдрическая	sp3, d3s	Ni(CO)4; [Co(NHз)4]2+
	Плоская	Dsp2	[Ni(CN)4]2-
5	Тригональная бипирамида	dz2sp3, d3sp	Fe(CO)5
	Квадратная пирамида	dx2-y2sp3, d3sp, d4s	[MnCI5]2-
6	Октаэдрическая	d2sp3	Cг(CO)6; [Co(NHз)6]з+
	Тригональная призма	d4sp, d5p, d3p3	Re[(Ph2C2S2)]3
	Пентагональная бипирамида	D3sp3	[Mo(CN)7]5-; [UO2F5]3-
7	Одношапочный октаэдр	d5sp, d4sp2	Mo[(CN(трет-C4H9))]6
8	Додекаэдр	d4sp3	[Mo(CN)8]4-
	Квадратная антипризма	d5p3	[TaF8]3-

Химическая связь в координационных соединениях образуется либо при интерференции дважды занятых электронами АО лигандов и вакантных АО центрального атома (донорно-акцепторная связь), либо при образовании многоцентровых связывающих МО, делокализованных в пределах координационного узла. В зависимости от природы взаимодействующих атомов, возможны различные способы описания химической связи в координационных соединениях. Мы будем рассматривать далее главным образом соединения d-элементов.

Таблица 3.10 Представления симметрии для d-орбиталей при различных случаях симметрии

координационное число	конфигурация	точечная симметрия	АО и их симметрийные обозначения
			dz2	dx2-y2	dxy	dxz	dyz
4	Тетраэдр	Td	е	е	t2	t2	t2
4	Квадрат	D4h	a1g	b1g	b2g	e	e
5	Квадратная пирамида	С4V	a1	b1	b2	е	е
5	Тригональная бипирамида	D3h	a1	е'	е'	е"	е"
6	Октаэдр	Oh	eg	eg	t2g	t2g	t2g

 

Спектрохимический ряд

Важно получить представление о порядке величин А= 10Dq. Эти значения могут быть взяты из экспериментальных данных о спектрах поглощения октаэдрически координированных ионов, обладающих одним электроном в d-оболочке (терм основного состояния ²D). Большой экспериментальный материал по электронным спектрам поглощения комплексов и оценочные расчеты позволили сформулировать ряд правил о зависимости величины 10Dq от типа центрального иона и лиганда. Наиболее важное из них правило спектрохимического ряда:

Величина 10Dq возрастает слева направо в следующем ряду наиболее характерных лигандов, причем указанный порядок не меняется для различных центральных ионов:

I^- < Br ^- < SCN ^- < Cl ^- < NO₃^- < F ^- < OH ^- < H₂O < NCS ^-<

< CH₃CN < NH₃ < Py < En < NO₂^- < CN ^- < CO , (3.47)

где Ру - пиридин; En - этилендиамин.

Отметим еще два достаточно общих положения.

1) При одинаковом лигандном окружении наибольшая величина 10Dq соответствует комплексам центральных ионов с наибольшими зарядами. Например, 10Dq для [Со(Н₂О)₆]³⁺ равна ~20 000 см ^-1, а для [Со(Н₂О)₆]²⁺ ~9700 см ^-1.

2) Величина 10Dq для комплексов ионов переходных металлов, принадлежащих к разным периодам периодической системы, но имеющих одинаковую электронную оболочку, примерно постоянна при однотипном лигандном окружении.

Таблица 3.13. ЭСКП для комплексов центральных ионов с различными электронными конфигурациями (в единицах Dq) в различных полях лигандов

 

Теория поля лигандов

Теория кристаллического поля, рассматривающая только АО центрального иона в поле точечных лигандов, неприменима к p -комплексам, к донорно-акцепторным связям, к анализу деталей связывания в комплексах. Наиболее общий подход к рассмотрению электронной структуры комплексов связан с расчетами волновых функций комплекса как целого. Для координационных соединений обобщения, полученные на основе метода МО, называются теорией поля лигандов. Главная особенность ее состоит в том, что ввиду обычно высокой симметрии координационного узла МО молекулы или иона координационного соединения классифицируются по симметрийным свойствам и принципиальную схему их образования из орбиталей лигандов часто можно построить, не проводя конкретных расчетов.

МО координационных соединений с лигандами, имеющими s -орбитали.

Рассмотрим вначале случай комплексов, образуемых лигандами L типа (СН₃)₃Р, МН₃, Н₂О, ОН^-, Н^-, которые используют для связывания с центральным атомом металла неподеленной гибридной пары электронов или пары электронов на s-орбитали (гибрид-ион). Наиболее характерный тип координации - октаэдрический. Координационные связи в комплексе ML₆^к+, где М - переходный металл, образуются при донировании электронов с s -орбиталей лигандов на вакантные 3d-, 4s-, 4p-орбитали металла (для атома металла третьего периода). Чтобы рассчитать валентные МО комплекса, выберем координатные оси, как показано на рис. 11.11, расположив вдоль них лиганды.

Полный базис валентных АО состоит из 15 орбиталей: девяти - металла, шести - лигандов. Только такие комбинации лигандных АО будут формировать МО с различными орбиталями металла. Соответствующие комбинации s -АО лигандов называются групповыми орбиталями). Они представлены в табл. 3.14.

Таблица 3.14.

Валентные орбитали металла и групповые орбитали лигандов в октаэдрическом комплексе ML (связывающие комбинации)

Металл	Лиганд	Представление симметрии
4s		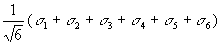а1g
4px		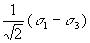t1u
4ру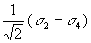
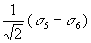
3dz2 (3dz2-x2-y2)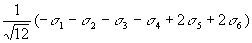
3dx2-y2		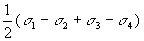eg
3dxy, 3dxz, 3dyz	-	t2g

Рис. 11.12,а иллюстрирует выбор групповой орбитали е-симметрии, комбинирующейся с d_x2-y2-орбиталью металла. Из рис. 11.12,б ясно, почему любая комбинация s -АО лигандов дает нулевое перекрывание с d-орбиталями металла типа t_2g.

На рис. 11.13 показана качественная корреляционная диаграмма МО октаэдрического комплекса, согласующаяся с данными прямых расчетов электронного строения разнообразных комплексов ML₆^к+. Из нее следует, что в комплексе, образованном s -лигандами и центральным атомом переходного металла, имеется шесть связывающих (a_1g, t_u1, 1e_g) и три несвязывающих (t_2g) валентных электронных уровня, на которых можно разместить 18 электронов. Если каждый из шести лигандов октаэдрического комплекса вносит по 2 s -электрона, то устойчивой конфигурацией центрального иона или атома будет 6-электронная.

В согласии с теорией кристаллического поля граничными орбиталями комплекса являются орбитали t_2g и 2е_g-типа. Однако если t_2g-орбитали в случае комплексов с s -лигандами действительно представляют собой локализованные d-орбитали центрального атома, то 2е_g-орбитали делокализованы и содержат вклад орбиталей лиганда. Поскольку эти орбитали имеют антисвязывающий характер, их заселение ведет к разрыхлению связей М-L. Так, для низкоспинового комплекса [Со(NН₃)6]3⁺, в котором 2е_g-орбитали не заселены, длины связей Со-N равны 1.94 Å, тогда как в высокоспиновом комплексе [Co(NH₃)₆]²⁺, где эти орбитали заполняются, длины связей Со-N увеличиваются до 2.11Å.

МО координационных соединений с лигандами, имеющими р- и p -орбитали.

В общем случае лиганды L, например галогены, могут образовывать связи с центральным ионом также за счет своих р-АО, оси которых ориентированы перпендикулярно связям М-L. При этом создается возможность p -связывания двух типов. На рис. 11.14, показаны два вида групповых p -орбиталей лигандов.

Групповые орбитали первого типа способны образовать p - МО комплекса при перекрывании с р-АО металла. Групповые орбитали лигандов способны к перекрыванию с t_2g-AO металла. Учет p - связывания приводит к включению этих орбиталей в комплексах типа [СоF₆]^3- в связывающие и антисвязывающие комбинации с орбиталями лигандов, тогда как в комплексах типа [Со(NH₃)₆]³⁺ t_2g – орбитали имеют несвязывающий характер. Именно этот эффект объясняет возможность образования дативных связей металла с лигандами, обусловливающих передачу электронной плотности с заполненных t_2g -AO металла на вакантные р- и p *-орбитали лиганда.

Другая особенность образования связей центрального атома металла с лигандами, обладающими р-орбиталями, состоит в том, что последние образуют отдельную систему рp -орбиталей t_2u-симметрии. Они вместе с s -орбиталями той же симметрии могут взаимодействовать с р-АО (t_1u) центрального атома металла. Поскольку s -перекрывание намного больше, чем p -перекрывание, можно в первом приближении пренебречь p -взаимодействием и отнести рp -ряд лигандных орбиталей t_1u -симметрии к несвязывающему типу. Это дает возможность рассматривать комплексы с заполненными электронами р-орбиталями (галогены) в рамках схемы, представленной на рис.11.13).

Наиболее важен эффект взаимодействия d-AO центрального атома металла с вакантными p *-орбиталями лигандов СО и СN в карбонильных и цианидных комплексах. На рис. 11.15 показана структура одной из t_2g -MO гексакарбонила хрома Сr(СО)₆, образующейся при перекрывании d_xy-AO металла с антисвязы-вающими p *-МО оксида углерода. Центральный атом в Сr(СО)₆ лежит в центре почти идеального октаэдра из атомов О и образует с лигандами как s -, так и p -связи. На рис. 11.16 дана корреляционная диаграмма МО гексакарбонила хрома, построенная с учетом p - и p *-орбиталей лиганда.

Для большей ясности s -орбитали различных типов даны в виде одного общего уровня. Расщепления, вызываемые взаимодействиями АО металла с p - орбиталями лигандов, которые можно скомбинировать в групповые орбитали, пользуясь соображениями симметрии, сравнительно малы. Как и в случае лигандов с р-орбиталями, можно рассматривать эти взаимодействия (за исключением t_2g-p -взаимодействия) как второстепенные по сравнению с взаимодействиями d-s -типа. В то же время эффект примешивания p*-орбиталей лиганда к t_2g-орбиталям металла играет важную роль, он приводит к увеличению расщепления t_2g- e_g уровней. Шесть СО-групп гексакарбонила хрома вносят 12 электронов неподеленных электронных пар, 24 p -электрона, а атом хрома дает 6 электронов. Таким образом, 21 связывающая МО в гексакарбониле хрома занята 42 электронами.

Детали химической связи в комплексных соединениях хорошо выявляют карты деформационной ЭП. Выбрав локальную систему координат на центральном атоме комплекса и сопоставляя пространственные характеристики валентных АО с положениями максимумов и минимумов d r , можно дать качественную трактовку карт d r в терминах орбитальных представлений. Такая трактовка носит, конечно, лишь приближенный характер, поскольку молекулярные (или кристаллические) орбитали не являются точной суперпозицией малого числа валентных АО.

Рассмотрим рассчитанную неэмпирическим методом Хартри-Фока в расширенном базисе стандартную деформационную ЭП гексакарбонила хрома Сг(СО)₆ (рис. 3, а ). В молекуле СО, являющейся здесь лигандом, число валентных электронов равно 10 и в основном состоянии электронная конфигурация этой молекулы приведена выше (раздел 3. .). В несвязывающую s -МО больший, вклад вносит АО атома С, что проявляется на стандартной деформационной ЭП в виде положительного максимума позади этого атома (рис. 10, д). В Сr(СО)₆ происходит смещение пары электронов от лиганда к иону металла через s - связь (s - донирование или донорно-акцепторная связь) и частичный обратный переток электронов к лиганду через p*-связь (обратное s - и p - донирование или дативная связь). Описанная картина хорошо согласуется с рентгеноспектральными данными.

Стандартная карта деформационной ЭП Сr(СО)₆ показывает, что для s -связи, ориентированной вдоль линии Сr-СО, характерно наличие минимума d r , лежащего вблизи атома Сr и переходящего ближе к атому С в максимум. Этот максимум несколько вытянут перпендикулярно линии Сr-СО. Эти карты dr прекрасно согласуются с описанной выше картиной химической связи в Сr(СО)₆. Однако специфика донорно-акцепторной химической связи на стандартной карте dr не проявляется. Выясним теперь, какая часть ЭП, аккумулируемая между атомами Сr и С, связана с образованием связи, а какая относится к неподеленным электронным парам атома С. Для этого рассмотрим “фрагментную” деформационную ЭП (рис.3. ,б) - разность между ЭП Сr(СО)₆ и фрагментами Cr(CO)₅ и СО при той же геометрии. Эта функция должна отражать именно донорно-акцепторное взаимодействие. И действительно, на соответствующей картее пик dr имеет существенно меньшую высоту и его максимум заметно смещен к середине межъядерного расстояния Сr-О. Он также вытянут перпендикулярно линии Сr-СО, т. е. отражает наличие p -компоненты во взаимодействии центральный атом-лиганд.

Расчет показывает, что электронные заселенности Зd орбиталей атома Сr в Сr(СО)₆, показывают (табл.3.15), что t_2g-AO атома Сr действительно имеют большую заселенность, чем e_g-AO.

Таблица 3.15.

Электронные заселенности орбиталей Сr в Сr(СО)₆

Орбиталь	C учетом 4s-AO	Без учета 4s-AO	Теория Хa -метод	Сферический атом
eg	1.42(5)	1.37(7)	1.12	2
t2g	3.40(5)	3.32(8)	3.26	3
Сумма	4.82(9)	4.69(9)	4.38	5
4s	1	-	-0.085	1
4px	-	-	-0.011	-
4py	-	-	-0.011	-
4рz	-	-	-0.011	-

 

Правило 18 электронов

Обобщение расчетных результатов и экспериментальных данных позволило сформулировать следующее правило: в устойчивых комплексах переходных металлов МL_n общее число электронов на связях M-L и несвязывающих электронов центрального атома равно 18.

Действительно, рассмотрим диаграмму орбитальных взаимодействий валентных s- p- и d-АО (общее число равно 9) с n симметризованными s -орбиталями лигандов L в комплексе МL_n (рис. 3. ). Подходящие по симметрии n АО центрального атома образуют с орбиталями лигандов n связывающих и n разрыхляющих МО. (9-n) орбиталей центрального атома, имеющих иную симметрию, образуют несвязывающие МО. Ясно, что на связывающих и несвязывающих МО можно разместить как раз 18 электронов.

рис. 3. Минкин с. 452, рис.11.22

Существует немало отклонений от правила 18 электронов. Например, плоские тетракоординированные и трикоординированные комплексы переходных металлов устойчивы при 16-электронной координации.

Эффект Яна-Теллера

Приближение Борна-Оппенгеймера позволяет, разделив движение электронов и ядер, использовать для анализа химических проблем только электронное уравнение Шредингера. Существует, однако, важный случай, когда поверхности потенциальной энергии, отвечающие различным электронным состояниям, настолько близки (или даже касаются друг друга), что электронные состояния в результате ядерного движения смешиваются (вырождение состояний). Возникают объединенные электронно-ядерные состояния, называемые вибронными, и электронное движение уже более неотделимо от ядерного.

Анализ показывает, что системы, где волновая функция вырождена (например, октаэдрические и плоские комплексы d-элементов), структурно неустойчивы: всегда существуют деформации ядерной конфигурации, понижающие ее симметрию и снимающие вырождение (эффект Яна-Теллера).

Пересечение адиабатических поверхностей (эффект Яна-Теллера первого порядка) имеет место в высокосимметричных системах с частично заполненными связывающими и несвязывающими МО. Встречается также ситуация, когда вырождение электронных состояний отсутствует, но орбитальное вырождение сохраняется - псевдоэффект Яна-Теллера.

Структурные деформации высокосимметричных координационных полиэдров многих комплексных соединений из-за эффектов Яна-Теллера могут носить как статический, так и динамический характер. В первом случае происходит стабилизация структуры за счет понижения симметрии. Во втором искажение сравнительно мало и приводит к структурам, занимающим неглубокие минимумы на ППЭ системы: эти структуры совершают быстрые переходы между несколькими эквивалентными ядерными конфигурациями, т.е. находятся в состоянии вырожденного динамического равновесия. Статический или динамический характер искажения Яна-Теллера зависит от того, насколько сильно уменьшение энергии системы зависит от деформации ядерной конфигурации. Если эта зависимость значительна и обеспечивает достаточную стабилизацию при понижении симметрии комплекса, соответствующее структурное искажение имеет статический характер.

Примером статического эффекта Яна-Теллера служат октаэдрические комплексы иона Сu²⁺. Девять d-электронов центрального иона могут разместиться на орбиталях t_2g- и е_g-типа двумя равноценными способами (рис. 11.23) и основное электронное состояние комплексов Сu²⁺ в октаэдрическом окружении является дважды вырожденным (²E_g). Эффект Яна-Теллера первого порядка приведет либо к удлинению, либо к сжатию октаэдра - так называемое тетрагональное искажение (рис. 11.24). Это искажение может быть легко объяснено с помощью анализа электростатических взаимодействий. Так, если в электронной конфигурации частично заполненной будет d_x2-y2-орбиталь, лиганды в положениях 1, 2, 3, 4 будут сильнее притягиваться к центральному иону, что приведет к увеличению расстояний М-L₅, М-L₆ по сравнению с остальными. Тетрагональное искажение имеет место в октаэдрах, окружающих ион меди в кристаллической решетке (СuС1₂)_n, и во многих других системах.

Другой пример статического эффекта Яна-Теллера дает структура координационного узла высокоспинового комплекса [МnF₆]^3- в кристалле МnF₃. Полиэдр здесь ромбически искажен вследствие двукратного вырождения (t_2g)³(e_g)-конфигурации и характеризуется тремя различными длинами связей Мn-F (1.79, 1.91 и 2.09 А). В транс-ацетилацетонате марганца две связи Мn-О имеют длину 1.948 А, а четыре другие-2.0 А.

При электронном вырождении, обусловленном заполнением t_2g- орбиталей, эффект Яна-Теллера выражен значительно слабее и носит обычно динамический характер.

Путь химической реакции.

Неоднократные попытки разработать общий алгоритм для локализации переходного состояния привели к концепции пути химической реакции. Согласно классическому определению Эйринга и Поляни (1931 г.), путь химической реакции - это путь минимальной энергии реакции, соединяющий соседние минимумы ППЭ через седловую точку переходного состояния. Путь минимальной энергии на сечениях ППЭ реакции обмена обозначен штриховой линией (Рис. 4), реакции изомеризации молекулы азациклобутадиена – жирной сплошной линией (Рис. 5). На сечении ППЭ реакции изомеризации 2-фторэтильного катиона (Рис. 6) из ряда альтернативных вариантов может быть выбран единственный путь минимальной энергии, соединяющий локальные минимумы двух метастабильных изомеров через два последовательные переходные состояния.

На основе определения пути минимальной энергии реакции был развит метод координаты реакции : сложным характером реакции пренебрегают и выделяют один структурный параметр, монотонное варьирование которого должно описывать ход реакции энергетическим профилем (типа представленного на Рис. 5, б)). Однако оказалось, что этот метод работает только в случае мономолекулярных реакций диссоциации или образования выделенной локализованной связи и в случае бимолекулярных S_N2 реакций, в которых разрыв и образование связи происходит синхронно. В остальных случаях координата реакции является линейной комбинацией структурных параметров реагирующей системы. Представление ее единственным параметром может привести к серьезной ошибке : не имеющему физического смысла гистерезису путей прямой и обратной реакций ( например, реакция СН₂ + Н₂ ß à CH₄). Суть сказанного поясняется на примере гипотетической реакции А ß à B.

На Рис. 8 представлена двухпараметрическая ППЭ реакции А ß à B. Выберем в качестве координаты реакции параметр х. Если двигаться из локального минимума А, на каждом шаге увеличивая координату х и минимизируя энергию по параметру у, то мы получим энергетическую кривую, изображенную жирной линией, которая не проходит через переходное состояние. Если аналогичным образом двигаться в обратном направлении из минимума В, постепенно уменьшая координату х, то в минимум А мы не попадем вообще. Путь реакции, изображенный пунктирной линией, является функцией двух переменных х и у.

Позже, в качестве пути реакции предлагалось рассматривать путь градиентного или скорейшего спуска, возникающий при оптимизации геометрии реагирующей системы по упомянутым выше методам градиентного спуска. На основе этих представлений был развит метод Мак-Ивера, используемый в ряде современных квантовохимических программных комплексов, таких как MOPAC и GAMESS.

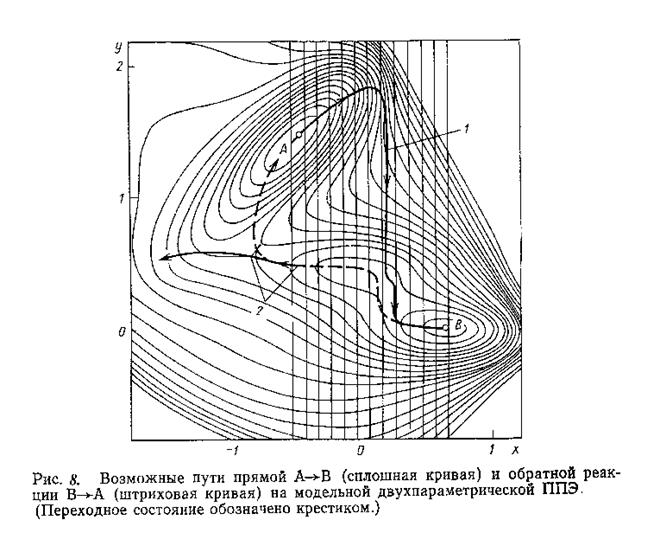В этом методе локализация переходного состояния осуществляется, исходя из того, что ему отвечает точка локального максимума на ППЭ, удовлетворяющая условию (5.8). Основным отличием этого метода от метода Дэвидона-Флетчера-Пауэлла является изменение знака градиента в уравнениях метода скорейшего спуска, обеспечивающее движение к максимуму ППЭ. К сожалению, (8) является необходимым, но не достаточным условием того, что найденная точка будет отвечать одномерному максимуму. Таким образом, без определения собственных значений гессиана (9) этот метод не гарантирует локализацию переходного состояния.

Камнем преткновения в развитии концепции пути химической реакции явилась обнаруженная неинвариантность этого пути относительно ортогонального преобразования координат. При этом инвариантными оказываются только стационарные точки ППЭ. Поэтому в настоящее время в квантовой химии реакций фигурирует теория переходного состояния, рассматривающая только стационарные точки ППЭ.

Роль орбитальной симметрии

Часто для описания реакции достаточно сведений о ее стадиях, определяющих сбли-жение реагентов и тип переходного состояния. Метод молекулярных орбиталей (МО) играет здесь важную роль. Вудворд и Хоффман сформулировали принцип сохранения орбитальной симметрии (1965 г.), выполняющийся для реакций без промежуточных продуктов (согласованных реакций). Этот принцип позволяет в ряде случаев предсказы-вать, будет ли соединение А реагировать с соединением В, по какому пути пойдет реак-ция и каких продуктов следует ожидать. В этом подходе рассматриваются структура активных МО реагирующих веществ и знаки АО, составляющих МО.

Правило Вудворда-Хоффмана: реакция называется разрешенной по симметрии, если в ходе ее симметрия активных МО сохраняется.

К активным относятся все участвующие в реакции занятые и вакантные МО реагентов и продуктов. Деление реакций на разрешенные и запрещенные по симметрии осуществляется с помощью корреляционных диаграмм.

Правило Вудворда-Хофмана носит общий характер. Рассмотрим его применение к одной из реакций диенового синтеза (реакции Дильса-Альдера) –циклоприсоединения цис-бутадиена к этилену, в результате которой образуется циклогексен. Эта реакция относится к числу перициклических, т.е. таких согласованных реакций, которые протекают с образованием циклических (“замкнутых”) переходных состояний, играющих определяющую роль.

Симметрия предреакционного комплекса реакции циклоприсоединения цис-бутадиена к этилену (Рис. 10) определяется плоскостью симметрии Р. Рассмотрим верхние занятые p и нижние вакантные p ^* МО этого комплекса. Разделим их на симметричные (S) и антисимметричные (A) относительно плоскости Р и расположим в порядке возрастания энергии, определенном расчетом (Рис. 11). Классифицируем таким же образом активные МО продукта реакции циклогексена: верхние занятые p , s и нижние вакантные p ^*, s ^* МО вновь образованных двойной и двух ординарных СС связей (Рис. 11). Согласно Вудворду и Хофману, корреляционную диаграмму взаимодействия между реагентами и продуктом следует строить простым соединением МО с одинаковой симметрией ( S ® S и A ® A ), учитывая, что разность энергий МО должна быть минимальна. Если это возможно и ни одна из соединяющих линий не пересекает нулевого уровня (правило непересечения), то реакция “разрешена” по симметрии. В результате, получаем корреляционную диаграмму Вудворда-Хоффмана для реакции Дильса-Альдера, на которой связывающие МО реагентов взаимодействуют только со связывающими МО продукта, а разрыхляющие МО реагентов – только с разрыхляющими МО продукта – реакция разрешена.

Рис. 10 Предреакционный комплекс реакции Дильса-Альдера циклоприсоединения цис-бутадиена к этилену.

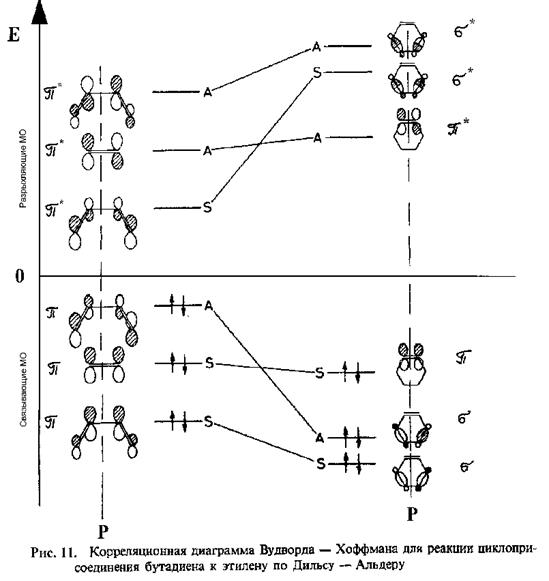
Правило Вудворда-Хоффмана может быть приложено и к реакциям замещенных полиенов, когда симметрия отсутствует. В этом случае рассматриваются корреляции между МО незамещенных аналогов. Так, с точки зрения правила Вудворда-Хоффмана становится понятно, почему при термической циклизации замещенного гексатриена в циклогексадиен образуется только продукт II, а в фотохимической реакции только продукт III (Рис. 12). Рассмотрим верхнюю занятую МО незамещенного гексатриена в основном электронном состоянии. Образование связывающей МО возможно только в результате дисротаторного (в разные стороны) поворота концевых групп, что и приводит к получению при термической реакции только продукта II. В фотохимической реакции вращению концевых групп предшествует переход молекулы гексатриена в электронно-возбужденное состояние. При этом электрон переходит с верхней занятой на нижнюю вакантную МО, преобразование которой мы теперь и должны рассматривать. Образование связывающей МО возможно только в результате конротаторного (в одну сторону) поворота концевых групп (Рис.12). Поэтому при фотохимической реакции получается только продукт IV.

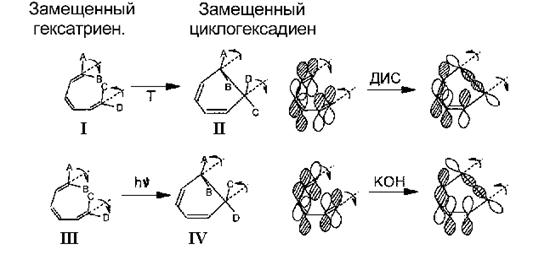
Рис. 12. Циклизация замещенного гексатриена в циклогексадиен: термическая дисротаторная I à II и фотохимическая конротаторная III à IV. Преобразование верхней занятой МО.

Запрет реакции по симметрии не обязательно означает, что реакция не может идти вообще. При отсутствии альтернативного “разрешенного” по симметрии пути, она может протекать только в жестких условиях с преодолением высокого активационного барьера. Так, энергия активации “запрещенной” реакции H₂ + D_{2 à} HD + HD составляет около 586 кДж/моль. Однако, если реакция “разрешена” по симметрии, это не обязательно означает, что ее активационный барьер низок. Например, энергия активации рассмотренной выше реакции Дильса-Альдера довольно значительна и равна 144 кДж/моль. Большие энергетические затраты на начальной стадии реакции вызваны согласованным растяжением 3 двойных связей, которые должны стать ординарными.

Эмпирически установленное правило Вудворда-Хоффмана было теоретически подтверждено впоследствии неэмпирическими расчетами по методу молекулярных орбиталей и проанализировано с помощью аппарата теории групп. При этом точкам пересечения линий на корреляционной диаграмме (смотри Рис. 11) были сопоставлены МО переходного состояния. Полученное таким образом положение переходного состояния относительно реагентов и продуктов согласуется с предсказаниями, полученными на основе постулата Хэммонда, обсуждавшимися ранее.

Таблица 1.

Индексы Уайберга I_СС, вычисленные при межатомных расстояниях, равных равновесным длинам связей R_CC в молекулах этана, этилена и ацетилена.

Молекула	RCC = 1.52 А	RCC = 1.34 А	RCC = 1.20 А
Н3С-СН3	0.99	1.03	1.07
Н2С=СН2	1.95	1.99	2.02
НС=СН	2.91	2.94	2.96

 

Молекулярный электростатический потенциал.

Распространенным и информативным статическим ИРС молекулы является кулоновский потенциал –молекулярный электростатический потенциал (МЭП). Его физический смысл следующий. Пусть заряд q₁ создает в точке пространства с радиус-вектором r МЭП V(r). Если в эту точку поместить точечный заряд q, то энергия электростатического взаимодействия между зарядом q и зарядом q₁ будет равна qV (в одноэлектронном приближении без учета поляризационной составляющей).В каждой точке r пространства внутри и вне молекулы МЭП имеет вид :

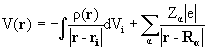(13)

где r (r) – электронная плотность, Za ï eï и R a - заряд и радиус-вектор ядра a .

Особый интерес для нас МЭП представляет потому, что необходимая для его расчета электронная плотность r (r) может быть не только рассчитана теоретически, но и получена косвенным образом из эксперимента по рентгеноструктурному анализу. Кроме того, именно МЭП определяет силы Гельмана-Фейнмана, действующие на ядра молекулы при их отклонениях от положения равновесия.

Лучший способ визуализации МЭП состоит в построении контурных карт изопотенциалов, создаваемых молекулами. Рассмотрим несколько примеров (Рис.13, 14):

1) Глубокие хорошо локализованные потенциальные минимумы показывают (Рис. 13), что молекула формамида будет протонироваться по неподеленным электронным sp²-парам атома кислорода.

2) Карты МЭП часто позволяют интерпретировать электрофильные и нуклеофильные свойства молекул в основном и электронно-возбужденном состояниях. Они чувствительны даже к малым изменениям молекулярной структуры. В последние годы это привело к использованию МЭП в качестве дескрипторов реакционной и селективной способности в QSAR-задачах. При этом только один из реагентов рассматривается в явном виде, а второй заменяется точечным зарядом. Их энергия взаимодействия рассчитывается без учета поляризационной составляющей. Случай взаимодействия краун-эфиров с положительными ионами дает иллюстрацию сказанному. Краун-эфиры – органические молекулы, имеющие неплоский макроциклический фрагмент (“корону”), образованный чередующимися атомами С и О – обладают различной селективной способностью по отношению к разным положительным ионам, захватывая некоторые из них внутрь полости молекулы. На рис. 14 показан МЭП в двух краун-эфирах : дибензо-18-краун-6 С₂₀Н₂₈О₆ и динитрилдибензо-18-краун-6 С₂₀Н₂₆ N₆О₁₀.

Рис. 14. МЭП краун-эфиров: дибензо-18-краун-6 С₂₀Н₂₈О₆ (а) и динитрилдибензо-18-краун-6 С₂₀Н₂₆ N₆О₁₀ (б). Области отрицательного потенциала обозначены пунктирными линиями (^... ), положительного потенциала – сплошными линиями ( ^_ ), поверхности нулевого потенциала – штрих-пунктирными линиями ( ^_._._ ).

В первой молекуле МЭП характеризуется отрицательной областью внутри полости, имеющей форму двухсторонней открытой воронки. Линии нулевого потенциала разделяют гидрофильные и гидрофобные части молекулы. Положительный однозарядный ион (ион щелочного металла), попав в область воронки, будет двигаться перпендикулярно эквипотенциальным поверхностям в центр полости, где потенциал максимально отрицателен (т.е. энергия взаимодействия максимальна), и там локализуется, образовав комплекс. В другой молекуле введение электрон-акцепторного заместителя NO₂ в бензольное кольцо, приводит к оттоку ЭП от макроцикла на периферию молекулы. Из-за этого МЭП в полости становится менее отрицательным и форма его изменяется: теперь он напоминает “закрытую” воронку (роль “крышки” играет поверхность нулевого потенциала). В этом случае образование комплекса с положительным ионом затруднительно, т.к. активационный барьер значительно выше. Все сказанное качественно объясняет наблюдаемое экпериментально экстракционное поведение обеих молекул.

Для существенно ионных соединений уже эффективные заряды на атомах в приближении “первого порядка” дают МЭП, пригодный для предсказания направления атаки при взаимодействии. МЭП позволяет оценить только электростатическую составляющую энергии ММВ Е_{эл/стат}. Но для корректного определения последней не меньшее значение может иметь, как известно, индукционная составляющая Е_инд., равная сумме поляризационной и дисперсионной энергий (Е_инд. = Е_пол. + Е_дисп.). Оценить Е_инд. позволяет рассмотрение взаимодействия граничных МО реагирующих молекул.

Таблица 2.

Граничная плотность электрона f_r. , а.е., на атомах дианионных форм ксантеновых красителей и более простые соединений I-V ^а) .

МО б)	Атом	I	II	III	IV	V
ВЗМО	С1а	0.46	0.46	0.46	0.48	0.48
	С2	0.19	0.18	0.19	0.19	0.19
	С3’	0.12	0.12	0.12	0.11	0.11
	С4	0.21	0.22	0.21	0.21	0.21
НВМО	С1а	0.68	0.65	0.68	0.62	0.66
	С1	0.18	0.15	0.18	0.16	0.18
	С2	0.10	0.06	0.11	0.09	0.13
	С10а	0.11	0.15	0.11	0.11	0.10

Примечание.^а) ;Химические названия соединений I-V и нумерация атомов даны на Рис.15 ; ^б) Структура граничных МО приведена с учетом наличия в соединениях I-V плоскости симметрии. Атомы с f_r. < 0.1 а.е. не указаны.

Предпочтительность взаимодействия “жесткий” - “жесткий” на первый взгляд не столь очевидна : с точки зрения орбитальных взаимодействий вариант “жесткий” - “мягкий” энергетически более выгоден. Клопман объяснил предпочтительность взаимодействия “жесткий” - “жесткий” тем, что жесткие соединения, обладая малым радиусом и незначительной поляризуемостью, являются источниками сильного электростатического поля. Выская энергия электростатического взаимодействия компенсирует небольшую стабилизацию предреакционного комплекса за счет взаимодействия граничных МО. Пирсон предложил другое объяснение, полагая, что частичные заряды на атомах жестких соединений больше, чем на атомах мягких систем. Отсюда следует предпочтительность взаимодействия “жесткий” - “жесткий”.

Концепция Пирсона охватывает два различных типа реакций: “контролируемые граничны- ми орбиталями” и “контролируемые зарядом”. Реакция считается орбитально контролируемой, если основным вкладом в энергию ММВ предреакционного комплекса является Е_инд. = Е_пол. + Е_дисп. В этом случае ВЗМО нуклеофила и НВМО электрофила отделены от других занятых и вакантных МО энергетической щелью не менее 1эВ. Реакция считается зарядово контролируемой, если основным вкладом в энергию ММВ предреакционного комплекса является Е_{эл/стат.} При этом величина энегетической щели, отделяющей ВЗМО нуклеофила и НВМО электрофила от других занятых и вакантных МО гораздо меньше 1 эВ. Так, рассмотренная выше реакция Дильса-Альдера, по крайней мере на начальных стадиях, является зарядово контролируемой, чем и объясняется ее достаточно высокий энергетический барьер. Реакция электрофильного замещения монозамещенных бензолов (Рис. 2) на стадиях I, III и IV является зарядово контролируемой, на стадии II – орбитально контролируемой.

Заметим, что поскольку МЭП отражает распределение полной плотности заряда, включаю- щей ядра, а не электронной плотности МО и, то он имеет предсказательную силу лишь в отношении реакций, контролируемых распределением зарядов на атомах. Граничная плотность электрона f_r на атоме r, напротив, определяет оптимальные места атак лишь в орбитально контролируемых реакциях.

 

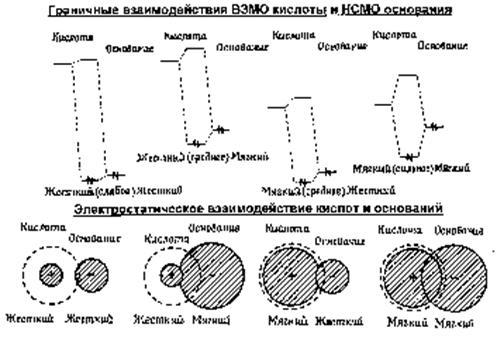
Рис. 16. Четыре возможных случая кислотно-основного взаимодействия. (В скобках указан тип взаимодействия с точки зрения теории ЖМКО).

Таблица 5.3.

Абсолютная мягкость S и жесткость h дианионных форм некоторых ксантеновых красителей и более простых соединений соединений, эВ^-1, эВ.

Соединение a)	Качественная оценка	S	h
I. Дианион 9-(2-карбоксифенил)-3,6-дигидроксиксантилия	Мягкий	0.154	3.248
II. Дианион 9-(2-карбоксифенил)-3,6-дигидрокситиоксантилия	Мягкий	0.160	3.132
III. Дианион 9-(2-карбоксипиридил)-3,6-дигидроксиксантилия	Мягкий	0.154	3.240
IV. Анион 9Н-3,6-дигидрокситиоксантилия	Мягкий	0.159	3.137
V. Анион 9Н-3,6-дигидроксиксантилия	Мягкий	0.154	3.241
VI. Анион 2-карбоксифенила	Жесткий	0.123	4.057
VII. Анион 2-карбоксипиридина	Жесткий	0.126	3.957

Примечание. ^a) Соединения I-VII представлены на Рис. 15.

Введение ИРС абсолютной жесткости h и мягкости S уничтожило четкую границу между жесткими и мягкими соединениями : каждой системе присущи оба эти свойства. Теперь понятие предпочтительности взаимодействий “жесткий-жесткий” и “мягкий-мягкий” заменяемся понятием предпочтительности взаимодействий соединений электрофильной и нуклеофильной природы с близкими значениями h и S.

Так, согласно значениям S и h (Таблица 4 ) в реакции электрофильного замещения у ароматического углерода :

С₆Н₅–X + СН₃–Y à Y- С₆Н₄–X + С₆Н₄, X = H, СН₃, NH₂, OН; Y = NO₂, F, I,

реакционная способность электрофильных молекул СН₃–Y будет возрастать в ряду повышения мягкости СН₃– NO₂ > СН₃–I > СН₃–F, а нуклеофильных молекул С₆Н₅–X – в ряду увеличения жесткости С₆Н₅-СН₃ > С₆Н₅-OН > С₆Н₅-NН₂ > С₆Н₅-Н.

Таблица 4.

Абсолютная мягкость (S) и жесткость (h ) некоторых органических соединений алифатической и ароматической природы.

Молекула	S	h

НУКЛЕОФИЛЫ

CH₃-H 0.055 9.127 CH₃-NH₂ 0.070 7.135 CH₃-OH 0.066 7.526 CH₃-С₆Н₅ 0.105 4.762 H- С₆Н₅ 0.140 3.579 NH₂- С₆Н₅ 0.110 4.537 OH- С₆Н₅ 0.110 4.567

ЭЛЕКТРОФИЛЫ

CH₃-NO₂ 0.090 5.585 CH₃-F 0.061 8.251 CH₃-I 0.088 5.691 I- С₆Н₅ 3.831 0.261 F- С₆Н₅ 0.444 1.126 NO₂- С₆Н₅ 0.965 0.518 CN- С₆Н₅ 0.536 0.933

Функции Фукуи.

Абсолютные жесткость h и мягкость S связаны с локальной жесткостью h (r) и локальной мягкостью s(r) функцией Фукуи f(r) :

s(r) = f(r) * S, (16)

h = f(r) * h(r).

Согласно определению Парра и Янга функциями Фукуи называются функции, определяющие локальные изменения электронной плотности r (r) при увеличении f⁺(r) или уменьшении f^-(r) числа электронов в системе :

f⁺(r) = r _N0+1(r) - r _N0(r), (17)

f^-(r) = r _N0(r) - r _N0-1(r).

Использование карт функций Фукуи для определения наиболее предпочтительных мест электрофильной, нуклеофильной и радикальной атак на примере молекулы Н₂СО представлено на Рис.17. Наиболее предпочтительным центром нуклеофильной атаки является атом углерода, которому соответствует глобальный максимум функции Фукуи f⁺(r), а электрофильной и радикальной атак - атом кислорода, которому соответствуют глобальные максимумы функции Фукуи f^-(r) и функции Фукуи f⁰(r), соответственно.

Рис. 17. Контурная карта функции Фукуи для молекулы Н₂СО (интервал между контурами 0.005 а.е.) : А. f⁺(r) в плоскости, перпендикулярной плоскости молекулы Н₂СО ; В. f^-(r) в плоскости молекулы Н₂СО ; С. f⁰(r) в плоскости, перпендикулярной плоскости молекулы Н₂СО. Координата атома углерода на оси абсцис 1.015 а.е., атома кислорода –1.27 а.е.

На Рис. 18 представлены характеристики нуклеофильных свойств молекул монозамещенных бензолов на примере молекулы бензальдегида – карты функции Фукуи f^-(r) и МЭП в плоскостях 1 и 2.

Рис. 18. Функция Фукуи и МЭП в молекулах монозамещенных бензолов: А. Схематический вид контурной карты функции Фукуи и МЭП (изображенный справа) получен совмещением сечений плоскостями 1 и 2. Плоскости 1 и 2 (изображенные слева) перпендикулярны плоскости ароматического кольца и проходят через атомы углерода в пара (р)- и мета (m)-положениях по отношению к заместителю Х (плоскость 1) и в мета (m)- и орто (о)-положениях (плоскость 2); Б. Контурная карта функции Фукуи f^-(r) молекулы С₆Н₅-CHO в плоскостях 1 и 2. Контуры соединяют точки с одинаковыми значениями функции f^-(r) : жирные линии - f^-(r) = 0, отрицательные значения f^-(r) уменьшаются, а положительные увеличиваются с интервалом между контурами 0.002 ; В. Контурная карта МЭП молекулы С₆Н₅-CHO в плоскостях 1 и 2. Контуры соединяют точки с одинаковыми значениями МЭП : жирные линии - МЭП = 0, отрицательные значения МЭП уменьшаются с интервалом между контурами 0.002, положительные - увеличиваются с интервалом между контурами 0.5.

Согласно карте функции Фукуи, электрофильная атака возможна по атомам углерода (m и о) в мета- и орто-положениях по отношению к заместителю Х = СНО, где значения функции f^-(r) положительны. Мета-положение, более предпочтительно, так как здесь плотность контуров больше. Электрофильная атака по атому углерода в паро-положение положении (р) существенно затруднена : значения функции f^-(r) в области атома р отрицательны. Теоретическая оценка относительной предпочтительности реакционных центров m > o >> p полностью совпадает с экспериментальной. Согласно карте МЭП относительная активность реакционных центров m >> p > o для атомов углерода в пара- и орто-положениях (р и о) противоречит эксперименту. Очевидно, молекула бензальдегида является существенно мягким соединением. Ее реакционную способность предсказывает карта функции Фукуи.

Таблица 5.

ИРС D на основе потенциала Морза и экспериментальные значения D_э

энергии связей CY для молекул YCX₃.

Параметрыа)	DССl3	HCCl3	HCF3	ClCF3	ICF3
De, см-1	32437.2	30675.3	38660.0	30500.0	19393.4
Eнк, см-1	1137.4	1487.3	1535.1	267.1	166.8
D, кДж/моль	374.5	349.2	444.2	361.7	230.0
Dэ, кДж/моль	369.2 ± 7 b)	358.2	446.4 ± 4.2	360.2 ± 3.3	231.5

Примечание. ^a) D_e – параметр потенциала Морза, Е_нк - энергия нулевых колебаний осциллятора СH (CD). 1 см^-1 = 1.1964807 10^-2 кДж/моль; ^b) Увеличение энергии связи в молекуле (CH₃)₃SiH при изотопном замещении H à D плюс D_э ( HCCl₃ ).

Этот ИРС развивает направление, связанное с расчетами в приближении реагирующей молекулы индексов энергии активации и теплового эффекта химической реакции, которые подробно рассмотрены выше. В случае связей локализованных в квантовохимическом смысле, при диссоциации по которым симметрия системы сохраняется, ИРС D совпадает по величине с энергией активации разрыва этой связи и предоставляет возможность оценки последней из колебательного спектра молекулы. Результаты апробации нового метода на примере определения энергии связи CY в молекулах вида YCX₃ представлены в Таблице 5. Теоретические и эксперимнтальные величины находятся в весьма удовлетворительном согласии.

Кластерные методы

Часто (например, при расчетах нестехиометрических кристаллов) целесообразно рассчитать лишь некоторый атомный или молекулярный фрагмент кристалла – кластер. Основной метод, используемый для это цели– метод Хартри-Фока. Одна из распространенных его кластерных модификаций – так называемый X a -метод. Корреляция электронов здесь по-прежнему игнорируется, а обменный потенциал представляется в виде:

V_x(r ) = -3a ((3/8p )r (r ))^1/3. (5.11)

Несмотря на кажущуюся упрощенность, Xa-метод дает хорошее количественное описание не только локализованных состояний, но и зонной структуры твердых тел. Для этого используют метод “погруженного” кластера: одноэлектронные функции раскладывают по базису из локализованных орбиталей и функций Блоха. Метод успешно применяется для изучения магнитных свойств веществ, химической связи и др.

Квантовая химия атома

Лекции-6.5 часов, семинар – 2 ч.

Принципы квантовой механики

Детерминант Слейтера

Метод Хартри-Фока

Квантовая химия молекул

Введение

Ограничения метода ХФ

Электронная корреляция

Теория возмущений

Метод валентных связей

Метод Парризера-Попла-Парра

Метод МО Хюккеля

Расширенный метод Хюккеля

2.25 Точность квантовохимических расчетов химических свойств молекул

к разделу "Лекции"

на основную страницу предметной комиссии по квантовой химии

3. ХИМИЧЕСКАЯ СВЯЗЬ И МЕЖМОЛЕКУЛЯРНОЕ ВЗАИМОДЕЙСТВИЕ
Введение

Эффект Яна-Теллера

Иллюстративный материал к разделу "Химическая связь и межмолекулярное взаимодействие"

к разделу "Лекции"

на основную страницу предметной комиссии по квантовой химии

Расчет особых точек ППЭ

Путь химической реакции

Роль орбитальной симметрии

Функции Фукуи

Литература

к разделу "Лекции"

на основную страницу предметной комиссии по квантовой химии

Лекции по курсу "Квантовая химия"

• Введение
• Квантовая химия атома
• Квантовая химия молекул
• Химическая связь и межмолекулярное взаимодействие
• Квантовохимическое описание реакций
• Квантовая химия конденсированных сред

на основную страницу предметной комиссии по квантовой химии

 

КВАНТОВАЯ ХИМИЯ

Библиографический список

1. Цирельсон В.Г., Бобров М.Ф., Апостолова Е.С., Михайлюк А.И. Лекции по квантовой химии. РХТУ, 1998. –350 с.

2. В.И. Минкин, Б.Я. Симкин, Р.М. Миняев. Теория строения молекул. Ростов-на-Дону “Феникс”, 1997 – 560 с.

3. Р. Заградник, Р. Полак. Основы квантовой химии. М: Мир, 1979.

4. Дж. Марелл, С.Кеттл, Дж.Теддер. Химическая связь. М: Мир, 1980.

5. К.С. Краснов. Строение молекул и химическая связь. М: Высшая школа, 1985.

6. В.Г. Цирельсон. Химическая связь и тепловое движение атомов в кристаллах. -М.: Винити, 1993.

7. И.Б. Берсукер. Электронное строение и свойства координационных соединений. Л: Химия, 1986.

ЛЕКЦИИ

Лекции 1-4 КВАНТОВАЯ ХИМИЯ АТОМА

Введение. Предмет квантовой химии и ее роль в описании химических явлений и процессов. Принципы квантовой механики.

Вариационный принцип. Решение уравнения Шредингера. Приближение независимых частиц. Метод самосогласованного поля. Приближение центрального поля. Атомные орбитали и их характеристики. Антисимметричность электронной волновой функции. Детерминант Слейтера. Метод Хартри-Фока. Ограниченный и неограниченный методы Хартри-Фока.

Квантовохимическая трактовка решений уравнений Хартри-Фока. Электронные конфигурации атомов с точки зрения квантовой химии.

Лекции 5-8 КВАНТОВАЯ ХИМИЯ МОЛЕКУЛЫ

Приближение Борна-Оппенгеймера. Метод Хартри-Фока для молекул. Приближение МО ЛКАО. Уравнения Рутана. Ограничения метода ХФ.

Электронная корреляция. Метод конфигурационного взаимодействия. Теорема Бриллюэна. Теория возмущений. Метод валентных связей. Точность учета электронной корреляции. Расчет энергии диссоциации химических связей.

Иерархия методов квантовой химии. Неэмпирическая квантовая химия. Базисные функции для неэмпирических расчетов. Вид аналитических базисных функций. Номенклатура базисных наборов. Минимальный базисный набор. Расширенный базисный набор. Поляризационные и диффузные функции. Базисные наборы Попла. Роль базисных функций в описании свойств молекул.

Метод полного пренебрежения дифференциальным перекрыванием. Метод частичного (промежуточного) пренебрежения дифференциальным перекрыванием (INDO). Метод модифицированного частичного пренебрежения дифференциальным перекрыванием (MINDO). Метод модифицированного пренебрежения дифференциальным перекрыванием. Разделение s - и p -электронов. p -электроннное приближение. Метод Парризера-Попла-Парра. Метод МО Хюккеля. Расширенный метод Хюккеля. Точность квантовохимических расчетов химических свойств молекул.

Лекции 9-12.ХИМИЧЕСКАЯ СВЯЗЬ И МЕЖМОЛЕКУЛЯРНОЕ ВЗАИМОДЕЙСТВИЕ

Орбитальная картина химической связи. Конструктивная и деструктивная интерференция орбиталей. Молекулярные орбитали и их симметрийная классификация. Электронные конфигурации двухатомных молекул. Анализ заселенностей орбиталей по Малликену. Понятие о зарядах и порядках связей.

Пространственное распределение электронной плотности. Деформа-ционная электронная плотность. Топологическая теория химической связи. Электростатический и энергетический аспекты описания химической связи.

Описание электронной плотности в многоатомных молекулах. Локализация и гибридизация орбиталей. Орбитальное обоснование модели отталкивания электронных пар Гиллеспи и строение молекул. Химическая связь в координационных соединениях. Теория кристаллического поля и теория поля лигандов. Спектрохимический ряд. Комплексы сильного и слабого полей. Магнитные свойства комплексов. Энергия стабилизации кристаллическим полем. Теория поля лигандов. Эффект Яна-Теллера.

Квантовохимический анализ межмолекулярных взаимодействий. Оценка ван-дер-ваальсовых атомных радиусов. Донорно-акцепторные молекулярные комплексы. Специфические невалентные взаимодействия. Водородная связь.

Понятие о супрамолекулярной химии.

Лекции 13-14 КВАНТОВОХИМИЧЕСКОЕ ОПИСАНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ

Квантовохимическое описание химических реакций в газовой фазе. Поверхность потенциальной энергии (ППЭ) химической реакции. Путь химической реакции, координата реакции. Переходное состояние, активированный комплекс. Расчет поверхности потенциальной энергии химической реакции. Особые точки равновесных и переходных состояний. Расчет реагентов, продуктов, перед- и послереакционных комплексов. Правило Вудворда-Хоффмана. Методы описания химических реакций: теория возмущений, метод координаты реакции, метод граничных молекулярных орбиталей Фукуи.

Орбитальные модели взаимодействия молекул с поверхностью. Хемосорб-ция.

Лекции 15-16.ЭЛЕКТРОННАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ

Одноэлектронные волновые функции в кристаллах и методы их расчета. Приближение локальной плотности. Уровень Ферми. Плотность состояний. Зонная структура твердых тел и обусловленные ею свойства. Хa - метод. Кластерное приближение и его применение в квантовой химии координационных соединений.

ЗАКЛЮЧЕНИЕ. Квантовая химия как инструмент прогноза в химии.

СЕМИНАРСКИЕ ЗАНЯТИЯ

1. Атомные орбитали и их свойства. Энергии одноэлектронных состояний .

2. Молекулярная структура. Конформации молекул. Молекулярные орбитали.

3. Химическая интерпретация результатов квантовохимических расчетов.

Специфика неэмпирических и полуэмпирических методов. Источники

квантовохимической информации в ИНТЕРНЕТ.

4. Химическая связь в двухатомных молекулах.

ПРАКТИЧЕСКИЕ (КОМПЬЮТЕРНЫЕ) ЗАНЯТИЯ

1. Неэмпирический квантовохимический расчет молекулы (из заданного

списка) и интерпретация его результатов (4 часа).

2. Полуэмпирический квантовохимический расчет молекулы (из заданного

списка) и интерпретация его результатов (4 часа).

Российский химико-технологический

университет им.Д.И.Менделеева

Предметная комиссия по квантовой химии

В. Г. Цирельсон