Пример, файл ch7data2.sav: 10991 студент из 169 учебных заведений (2 и 4-х летнее обучение). Для случаев с непостоянным интервалом наблюдения должна быть уравновешивающая переменная, представляющая собой величину интервала наблюдения (или общее число возможных проб). Таким образом, этот случай описывается так:
E(Y/t) = 1/t E(Y) = λ/t
Одноуровневая модель с одним предиктором выглядит так:
η ij = log ( 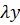 ) = β0 j + β1 X iy + log ( ty )
) = β0 j + β1 X iy + log ( ty )
т.е. в модель добавляется эффект этого уравновешивающего параметра.
Переменная смещения задается во вкладке Предикторы. Хокс (2010) отмечает, что ее нужно логарифмировать, чтобы она была в модели в той же метрике, что и ЗП (которая присутствует в модели в виде логарифма). Это всегда количественная переменная.
Оценим параметры такой модели:
η ij = β0 j + β1 ses + β2 gmmath + β3 male +β4 gmgpa + β5 twoyaer
Результат:
| Параметр | B | Стд. Ошибка | Проверка гипотезы | Exp(B) | ||
| Хи-квадрат Вальда | ст.св. | Знч. | ||||
| (Константа) | -,263 | ,0263 | 100,287 | 1 | ,000 | ,769 |
| ses | ,004 | ,0181 | ,043 | 1 | ,837 | 1,004 |
| male | ,168 | ,0284 | 34,728 | 1 | ,000 | 1,182 |
| gmmath | -,006 | ,0002 | 819,927 | 1 | ,000 | ,994 |
| gmgpa | -,327 | ,0176 | 344,916 | 1 | ,000 | ,721 |
| twoyear | ,195 | ,0290 | 44,961 | 1 | ,000 | 1,215 |
| (Масштаб) | 1a | |||||
Включая в уравнение разные члены, можно оценивать вероятность провала по курсу, например, для числа лет обучения:
ηij = -0,263+0,195= -0,068, возводим е в эту степень и получаем, что для девушек, учащихся по программе 2-х лет это будет 0,934. По сравнению с 4-х летним обучением это в 1,215 раз больше.
Используем в модели дополнительно переменную смещения – это логарифм числа лет обучения:
| Параметр | B | Стд. Ошибка | Проверка гипотезы | Exp(B) | ||
| Хи-квадрат Вальда | ст.св. | Знч. | ||||
| (Константа) | -1,972 | ,0261 | 5726,878 | 1 | ,000 | ,139 |
| ses | ,027 | ,0183 | 2,203 | 1 | ,138 | 1,028 |
| male | ,158 | ,0286 | 30,460 | 1 | ,000 | 1,171 |
| gmmath | -,007 | ,0002 | 893,082 | 1 | ,000 | ,993 |
| gmgpa | -,264 | ,0162 | 265,136 | 1 | ,000 | ,768 |
| twoyear | ,220 | ,0292 | 56,614 | 1 | ,000 | 1,245 |
| (Масштаб) | 1a | |||||
Получили достаточно большие различия, особенно в величине интерсепта (-0,263 против -1,972)с – поскольку оценку соответствующей частоты поделили на величину переменной смещения. Большинство других коэффициентов остались приблизительно такими же.
В одноуровневых моделях можно изменять метод оценки параметра масштаба (вкладка Оценивание), для это можно изменить метод оценки этого параметра, изменив его на хи-квадрат Пирсона, в этом случае программа сама вычислит этот параметр. Это может привести к более консервативным оценкам дисперсий и уровней значимости:
| Параметр | B | Стд. Ошибка | 95% доверительный интервал Вальда | Exp(B) | |
| Нижняя | Верхняя | ||||
| (Константа) | -1,972 | ,0279 | -2,027 | -1,918 | ,139 |
| ses | ,027 | ,0196 | -,011 | ,066 | 1,028 |
| male | ,158 | ,0302 | ,099 | ,217 | 1,171 |
| gmmath | -,007 | ,0003 | -,007 | -,006 | ,993 |
| gmgpa | -,264 | ,0167 | -,296 | -,231 | ,768 |
| twoyear | ,220 | ,0307 | ,159 | ,280 | 1,245 |
| (Масштаб) | 2,558a | ||||
При этом значения полученных коэффициентов не изменяется.
Этот параметр – 2,558, есть отношение оценки дисперсии (по Пирсону) к числу степеней свободы:
| Статистики согласияa | |||
| Значение | ст.св. | Значение/ст.св. | |
| Уклонение | 22726,791 | 10985 | 2,069 |
| Масштабированное уклонение | 8884,876 | 10985 | |
| Хи-квадрат Пирсона | 28098,737 | 10985 | 2,558 |
| Масштабированное значение хи-квадрат Пирсона | 10985,000 | 10985 | |
| Log-правдоподобиеb,c | -17201,622 | ||
| Скорректированный логарифм правдоподобияd | -6724,851 | ||
| Информационный критерий Акаике (AIC) | 34415,243 | ||
| Скорректированный информационный критерий Акаике (AICC) для выборки конечного объема | 34415,251 | ||
| Информационный критерий Байеса (BIC) | 34459,072 | ||
| Состоятельный информационный критерий Акаике (CAIC) | 34465,072 | ||
В процедуру GENLIN MIXED это тоже возможно для негативного биноминального распределения, где этот параметр может оцениваться.
Используем процедуру GENLIN MIXED:
- добавим в модель две переменные второго уровня – вузовские, воспринимаемое качество академизма в процессе обучения и качество объяснения материала на аудиторных занятиях;
- используем Пусссоновское распределение и лог-функцию связи.
- модель будет состоять из интерсепта + 5 внутришкольных предикторов + 2 междушкольных предиктора + 1 случайный эффект (случайная вариация интерсепта);
- во вкладке Вес и смещение укажем как переменную смещения число семестров;
- во вкладке Параметры конструкции укажем Использовать робастное оценива 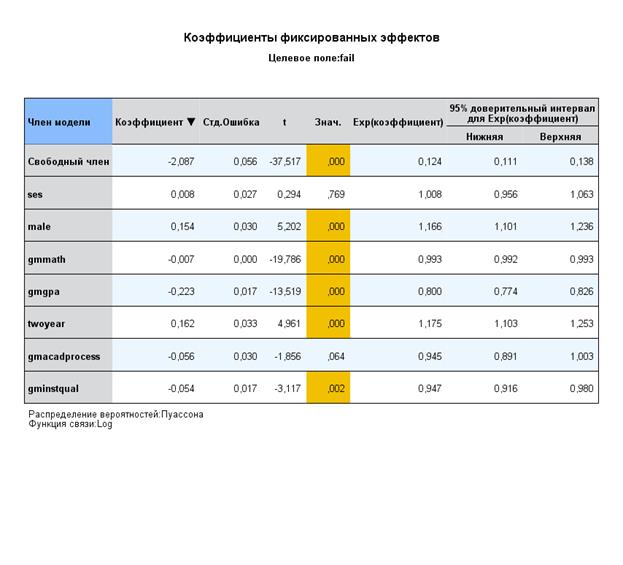
Вариант модели с использованием отрицательного биноминального распределения дает очень похожие результаты и такие же значения информационных критериев.
Подчеркивается, что строгое использование информационных критериев достаточно условно, поскольку оценки модели основываются на оценке квази-отношения правдоподобия.
Дата: 2019-02-19, просмотров: 374.