Для одноуровневых случаев используется процедура «Обобщенная линейная модель». Смысл интерсепта – это значение логарифма величины оценки в том случае, когда ВСЕ предикторы равны 0. Поэтому все НЗП нужно центрировать относительно 0-го среднего и единичной дисперсии.
В Пуассоновском распределении среднее и дисперсия равны. Когда дисперсия намного выше среднего нужна коррекция, но пока в СПСС этого нет. Однако, в этом случае используют отрицательное биноминальное распределение, которое позволяет компенсировать эту проблему (высокое значение дисперсии). Для этого используют опцию «Настраиваемая» и в ней выбирают этот вид распределения и логарифмическую функцию связи. При этом нужно задать значение параметра масштаба или поручить это сделать самой программе. Если мы обрабатываем модели без вложенных факторов, то для оценки оптимальности величины масштаба можно строго использовать информационные критерии по принципу выбрать модель с меньшим значением критерия.
Процедура GenLin Mixed.
В примере 7 используется негативное биноминальное распреление, а не Пуасоновское.
Для оценки каждого из компонентов дисперсии случайных факторов – интерсепта и к-л включенного в него фактора используется установка «Компоненты дисперсии». Если нужно также оценить их связь, то следует сделать установку «Неструктурированная матрица» ковариаций – этот вариант рассчитывает ВСЕ компоненты дисперсии.
Для построения и изучения 2-х уровневых моделей в список фиксированных эффектов добавляют не только внутрисубъектные факторы (то, чем различаются ) испытуемые, но также межсубъектные факторы – то, чем различаются единицы анализа (которые мы обозначили как субъекты).
Модели частотных данных с разным числом наблюдений (величина экспозиции, длительность интервала наблюдения, величина выборки, число возможных выборов и т.д), по которым рассчитываются частоты – процедура «Обобщенные линейные модели»:
Оценки параметров модели включает оценки логарифма частот. Для интерсепта – это оценка при нулевых значениях всех фиксированных факторов.
Для определения числа наблюдений ЗП во вкладке «Предикторы» задается переменная, соответсвующая смещению (т.е. числу наблюдений, по которому получена оценка частоты ЗП) – она должна быть количественной числовой переменной. Эта переменная не может быть одновременно предиктором.
Глава 6. Двухуровневые модели мультноминальных и порядковых данных.
При обработке мультиноминальных данных используется метод мультноминальной логистической регрессии. Это расширение бинарного случая (т.е. модели Бернулли), поскольку производится последовательное сравнение каждой категории и некоторой категорией, выбранной в качестве референтной. В результате мы получаем серию из n-1 сравнений, где n – это число категорий. Таким образом, это метод расчета множества оценок одних категорий относительно какой-то одной. В этом смысле анализ порядковых данных более однозначен, поскольку, выбрав в качестве референтной самый маленький или самый большой ранг, мы получаем однозначное сравнение – что больше, что меньше, что не различается.
Этот метод также применим для обработки порядковых данных (слабо порядковых данных или данных, относительно которых исследователь не совсем уверен в том, что они упорядочены), но не наоборот – порядковые логистические модели не подходят для обработки номинальных и мультиноминальных данных.
Когда мы анализируем влияние какой-либо НЗП на ряд упорядоченных категорий, то возникает вопрос о том, а одинаково ли влияние НЗП на все уровни ЗП (Нох, 2010)? С точки зрения линейной модели резонен вопрос: а всегда ли начиная с какой-либо упорядоченной категории X при увеличении X мы ожидаем увеличение Y?
Первый пример – ch6data1.sav. 43 школ, 9166 выпускников оценивали свои планы о продолжении обучения (три варианта – бакалавриат 4 года, колледж 2 года, ПТУ – объединены в одну категорию, не планирует продолжать обучение – это референтная категория), группирующие переменные – пол, соц-эконом. статус семьи учащегося, ряд НЗП переменных, характеризующих школу: академический профиль, сертифицированные учителя, общий соц-эконом. уровень учащихся в данной школе. Уровень 1 – индивидуальный: пол, планы на дальнейшее обучение. Уровень 2 – особенности школы.
Поскольку ЗП – мультиноминальная, то используем функцию связи logit.
Фактически в качестве основной оценки модели вычисляется логарифм отношения частот двух исходов для каждой из категорий по сравнению с референтной.
Рассмотрим одноуровневую модель: ЗП – 3-х альтернативный выбор школьника, предикторы – пол, соц.-эконом. уровень семьи и общий рейтинг учащегося.
Используем процедуру Genlin Mixed (Обобщенные линейные) с опцией «Робастное оценивание» и референтной категорией 2:
Для уровня 4 года обучения:
Интерпретация 
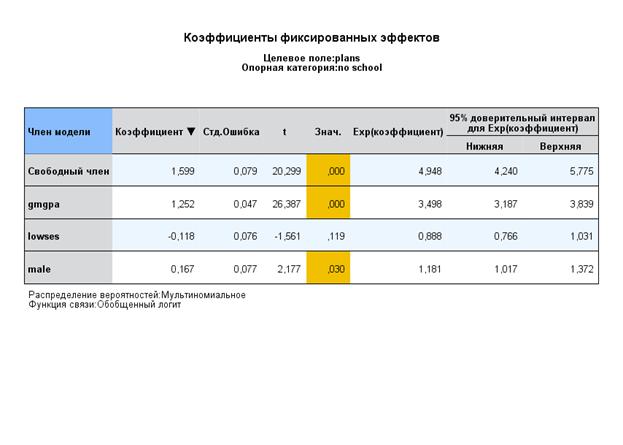
Интерпретация интерсепта: отношение правдоподобия частот выбора 4-х летнее обучение по сравнению с нежеланием учиться статистически достоверно значимо выше для школьников с показателями по всем НЗП =0, т.е. для девушек (0), из обеспеченных семей (0) и рейтингом выше среднего (0 – средний уровень). Это превышение статистически оценивается в 8,587 раза.
Интерпретация различий по НЗП:
Школьники с низким соц-эконом статусом более чем на 62% реже выбирают 4-х летнее обучение. Это тоже значимый эффект.
Школьники с высоким рейтингом в 7,62 раза чаще выбирают дальнейшее 4-х летнее обучение по сравнению с более низким рейтингом.
Различия в частотах выбора юношей и девушек статистически не достоверны.
Для уровня 2 года обучения:
Расширение модели за счет нестинга - включения респондентов в разные группы по уровням разных НЗП, т.е. включаем не один интерсепт, а несколько (т.е. сравнение средних и дисперисий по 43 школам, школа – случайный фактор), следовательно кратно увеличивается число решаемых уравнений. Таким образом, в модель включается и оценивается вариабельность интерсептов как случайный фактор.
Включаем в модель один фиксированный и один случайный фактор – интерсепт, оцениваем его вариабельность по 43 школам. Для этого кроме указания интерсепта как случайного фактора также указываем в качестве источника для комбинации испытуемых переменную школа и тип ковариации случайных эффектов «компоненты дисперсии».
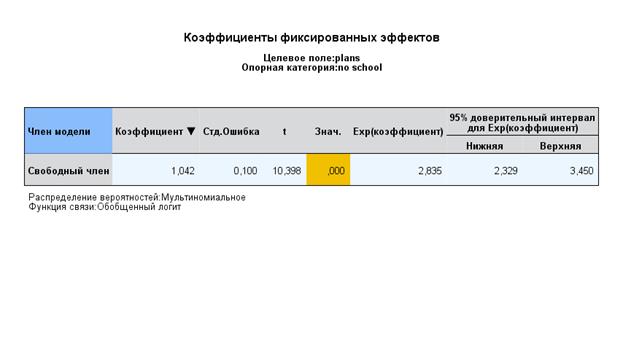
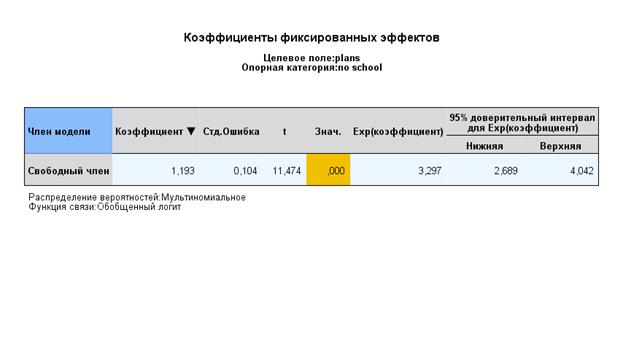
Интерпретация результатов:
Анализ вариабельности интерсептов показывает, что как для категории 1 (планы на обучение 4 года) – логарифм отношения правдоподобия=1,193, так и для категории 2 (обучение 2 года) – логарифм отношения правдоподобия=1,042 средний выпускник всех школ достоверно планирует продолжить обучение.
Анализ таблицы компонентов дисперсии второго уровня позволяет показать, какая вариабельность интерсептов для каждой из двух анализируемых категорий имеет место по школам и значима ли она: оказалось, что для каждой категории дисперсия значима.
Кроме того, зная дисперсию логистического распределения – 3,29, и эти величины, можно оценить их долю в общей дисперсии как к-т интерклассовой корреляции:
ρ=σ2между школами/σ2между школами + 3,29внутри щкол =0,381/3,671=0,104. Т.е. вклад различий между школами по категории 1 в общую дисперсию – чуть более 10%. , для категории 2 – 0,349/3,639=0,096.


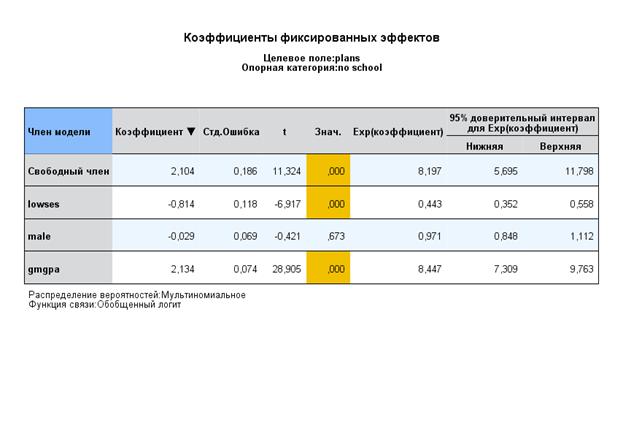
Далее мы можем включать в модель факторы первого уровня – пол, СЭС, средний рейтинг выпускника, или факторы второго уровня – лицензирование учителей, академический профиль школы, соц-эконом уровень учеников школы.
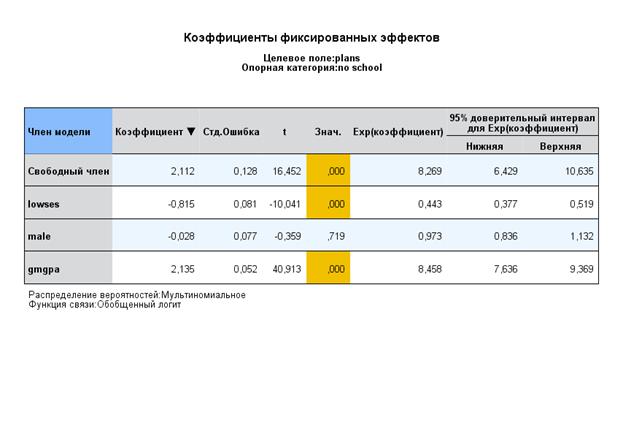
Таким образом, фактически мы оценили все члены уравнения, описывающего составные части итогового отношения правдоподобия для первой категории относительно второй:
η1ij = b0(1) + b1SES(1) + b2male(1) + b13gmpga(1) + u0(1)
или теперь в реальных числах:
η1ij = 2,112 – 0,815 - 0,0028 +2,135,
И, таким образом, можно оценить вклад каждого фактора в логарифм общего отношения правдоподобия, например, для SES:
η1ij = 2,112 – 0,815 = 1,297, это означает, что:
e1,297 = 2,718281,297 = 3,658, из этого следует, что по cравнению со средним по всей выборке влияние этого фактора (т.е. SES=0 – семья школьника имеет низкий уровень SES) уменьшает вероятность выбора выпускником 4-летнего обучения с 8,269 (e2,112) раза до 3,658 раза по сравнению с выбором прекращению обучения.
И для второй категории:
η2ij = b0(2) + b1SES(2) + b2male(2) + b3gmpga(2) + u0(2)
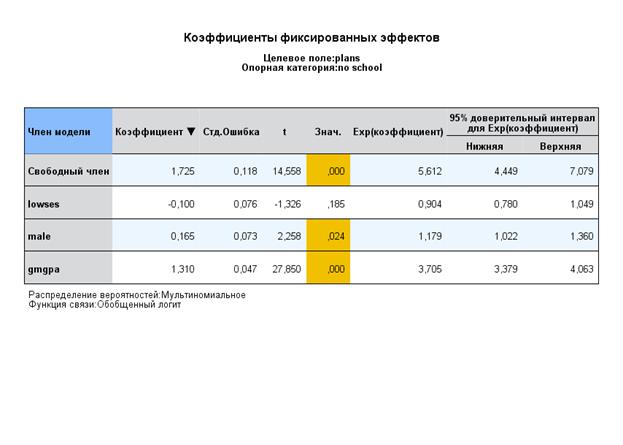
Мы можем также включать в модель оценку возможного вклада случайного фактора первого уровня (т.е. фактора индивидуальности учащегося), например, общего рейтинга учащегося (GPA) , т.е. будем учитывать параметр случайного наклона регрессионных прямых, связанных с рейтингом ученика, на втором уровне – уровне школ. Для этого кроме интерсепта включаем в уравнение один член - gpa-фактор. И будем оценивать вариацию наклонов регрессионных на множестве объектов – школ.
Фиксированные эффекты – 6 штук, почти те же (лишь немного изменились абсолютные значения коэффициентов).
Но особо обратим внимание на дисперсию компонент для случайного фактора, наблюдаемого на втором уровне - уровне школ. Фактически, когда мы включаем в модель случайный фактор, то мы должны указывать, на каком уровне (более высоко!) мы будем исследовать его вариацию. Она представлена в таблицу компонентов дисперсии для каждой из двух категорий:
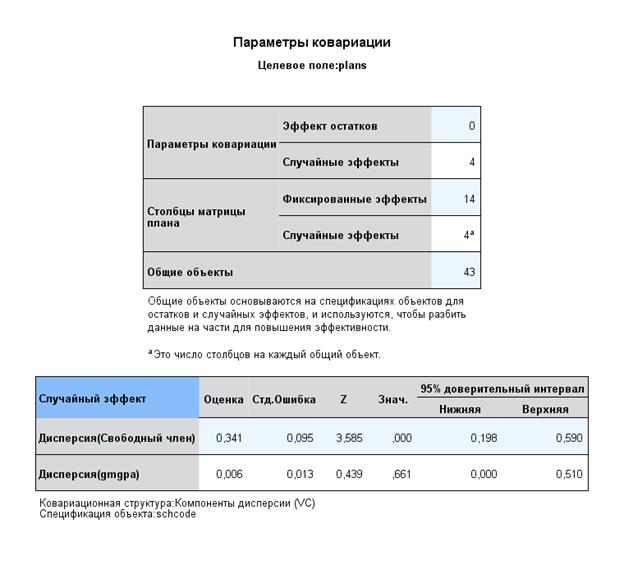
Что здесь представлено:
1) значимая вариация интерсептов на множестве из 43 школ, 2) вариация фактора GPA незначимой.
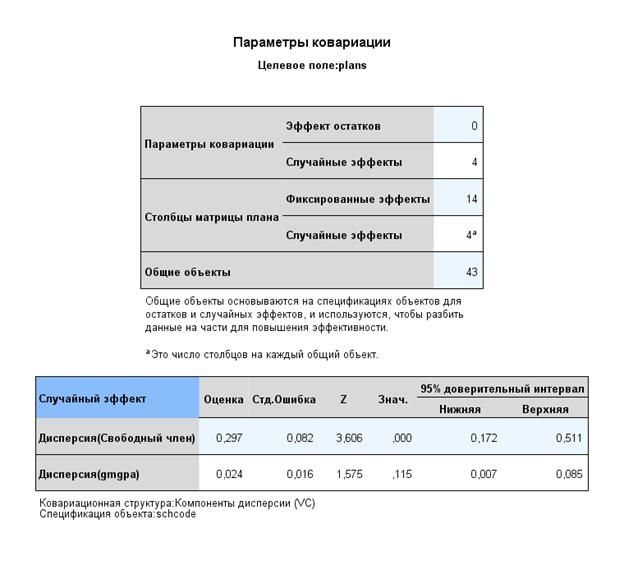
Для категории 2 (таблица ниже) – тоже самое. На небольшой выборке (43 школы) используемые критерии очень консервативны.
И для категории 2:
Дата: 2019-02-19, просмотров: 355.