В этих моделях предикторы могут быть как категориальными переменными, так и количественными ковариатами.
Порядковые модели предсказывают вероятность того, что ответ был дан на k-ой категории или ниже:
P(Y ≤ c) = π1 + π2+ … +πс
Поскольку модель представляет собой формулировку накопленной вероятности, то вероятность появления ранга с i или выше выражается как:
P(Y ≥ c) = 1 - P(Y ≤ c)
В отличии от вероятности отдельного события, в комулятивной (или пропорциональной) модели эта вероятность рассматривается как вероятность интересующего нас ранга и всех предшествующих ему рангов.
Например (как в рассматриваемом ниже файле), если ЗП имеет 3 упорядоченных категории (1 – отчислен из вуза, 2 – до сих пор числится, 3 – окончил вуз) для респондента i накопленные вероятности (в сумме равны 1) будут такими:
P(Y1i =1) = P(ci =1) = π1i
P(Y2i =1) = P(ci =1) + P(ci =2) = π2i
P(Y3i =1) = P(ci =1) + P(ci =2) + P(ci =3) = 1
Чаще всего распределение рангов представляется в виде модели мультиноминальным распределением и комулятивной логит или комулятивной пробит функциями связи.
Оценка комулятивной вероятности появления в данных ранга с i и ниже определяется по отношению в референтной c-ой категории, соответствующее отношение правдоподобия будет следующим:
ηic = log(P(Y ≤ c)/P(Y >c) = log (πi/1- πi), где с – ранговые категории.
Нужно иметь в виду, что в порядковых регрессионных моделях мы имеем дело не с вероятностями реальных данных, а с отношениями правдоподобия кумулятивных вероятностей модельных коэффициентов. Ключевая особенность порядковых моделей состоит в том, что для все регрессионных прямых допускается один и тот же наклон, что означает, что выбранные предикторы оказывают одно и тоже влияние на все порядковые категории (как в параллельных регрессионных моделях). Фактически в этих моделях предполагается, что для каждой категории существует свой порог (величина влияния предиктора ηic), выше которого дается соответствующий ответ: если величина предиктора меньше первого порога, то дается наименьшая категория, если больше первого порога и меньше равна второму порогу – наблюдается вторая категория, и, если ηic больше второго порога – наблюдается третья категория.
Поскольку пропорциональная вероятностная модель с комулятивной логит функцией связи фактически оценивает вероятность попадания ЗП переменной в отдельную категорию с или ниже ее (P(Y ≤ c), а Х – величина предиктора), то в литературе эта модель описывается такой линейной функцией:
η ic = log ( πic /1- πic ) = ac – b Х ,
где а – это увеличивающийся порог, разделяющий латентную переменную ηic на ожидаемые вероятности Y. Каждая логит-модель имеет свой порог (а) и наклон регрессионных прямых, равный для всех категорий – b.
Способ кодировки рангов определяет направление отношение правдоподобия и знак к-та b. Этот к-т (или бета) в таких моделях отражает увеличение в единицах отношения правдоподобия попадание ранга в категорию c и ниже в сравнении с опорной боле высокой категорией при увеличении Х на одну единицу. Таким образом, положительный к-т бета увеличивает отношение правдоподобия появления более самой высокой (референтной) категории (поскольку уменьшает вероятность оцениваемой относительно нее категории!), а отрицательный к-т – уменьшает. Поэтому знак к-тов в кумулятивной вероятностной модели нужно рассматривать наоборот по сравнению с соответствующей моделью множественной регрессии. Эта важно иметь в виду при интерпретации результатов: какая вероятность уменьшается или увеличивается относительно какой.
В СПСС допускается кодировать ЗП, упорядочивая их значения от меньшего к большему.
В разных пакетах (HLM, SPSS, Mplus)знак отношения правдоподобия может оцениваться по-разному. Это нужно иметь в виду при интерпретации результатов.
Очень полезно для каждой рейтинговой категории построить и проанализировать таблицу средних значений каждого предиктора, тогда будет проще оценивать полученные статистические результаты.
Пример - файл ch6data2.sav: что влияет на вероятность продолжения обучения в вузе. 6983 студента из 934 вузов.
Сначала строим одноуровневую модель порядковых данных с помощью процедуры GENLIN, модель – порядковая логистическая:
η ic = log ( πic /1- πi ) = ac + b1 Х zses + b2 Х hiabsent
Первый член – вклад школьного фактора (стандартизированные оценки соц-эконом. статуса студентов), второй – индивидуального (много – 1, или мало прогуливает - 0).
Оценки параметров модели:
- важно иметь в виду, что СПСС для интерпретабельности результатов инвертирует знаки коэффициентов (см. выше формулу и соответствующие пояснения);
- при константности остальных предикторов уровень SES позитивно связан с вероятностью остаться и продолжить обучение в вузе – увеличение SES на 1 сигму приводит к увеличению отношения правдоподобия на 0,925; т.е. чем выше этот уровень, тем более высока вероятность для студента продолжить обучение в вузе (или соответствовать более высокой рейтинговой категории ЗП);
- в логистических моделях для порядковых данных отношение правдоподобия представляет собой вероятность появления более высокой категории по сравнению со всеми более низкими категориями для каждой категории при увеличении предиктора на 1 единицу (в этом смысле очень удобно использовать стандартизированные значения НЗП – это отмечают и сами авторы книги); в данном примере при увеличении SES на 1 сигму вероятность перехода ЗП в след категорию увеличивается в 2,522 раза;
- и наоборот, отрицательные значения частоты прогулов уменьшают вероятность появления у ЗП более высокой категории, т.е. снижают шанс студента доучиться до конца (референтная категория – студенты с низким уровнем прогулов): вероятность студентов с кодом 1 (много прогуливают) увеличивает их шанс быть отчисленными на 18,9%. Тоже самое: уменьшение прогулов на 1 единицу увеличивает почти в 5 раз вероятность продолжить обучение.
| Параметр | B | Проверка гипотезы | Exp(B) | |||
| Хи-квадрат Вальда | ст.св. | Знч. | ||||
| Пороговое значение | [persist3=0] | -2,438 | 2793,506 | 1 | ,000 | ,087 |
| [persist3=1] | -2,043 | 2352,843 | 1 | ,000 | ,130 | |
| hiabsent | -1,664 | 256,633 | 1 | ,000 | ,189 | |
| zses | ,925 | 576,636 | 1 | ,000 | 2,522 | |
| (Масштаб) | 1a | |||||
Оценим эффект взаимодействия этих двух факторов:
η ic = log ( πic /1- πi ) = ac + b1 Х zses + b2 Х hiabsent + b1 Х zses × b2 Х hiabsent
Для этого во вкладке «Модель» нужно сначала установить «Взаимодействие», а затем, выделив оба фактора, перетащить их в правое окно – тогда в модель включиться эффект взаимодействия..
В результате получаем незначимый эффект межфакторного взаимодействия, т.е. прогулы снижают роль SES как предиктора вероятности студента доучиться до конца.
Пример 2: многоуровневая порядковая модель. Для этого используем процедуру GENLINMIXED.
Сначала рассмотрим необусловленную модель, т.е. модель без предикторов с одним интерсептом. Для респондента i и школы j имеем следующее выражение:
η cij = log ( πcij /1- πcij ) = ac + b о j
Отметим, что интерсепт – первый порог, может варьировать по школам, но второй порог – это фиксированный параметр.
Используем мультноминальную логистическую регрессию, модель с двумя фиксированными факторами (два интерсепта – для категории 0 и 1) и одни случайный фактор (вариация интерсептов по школам).
Оценив интерсепты по каждой категории, можно получить оценки вероятности для каждой из категорий - η cij = log ( πcij /1- πcij ):
Для категории 0: 0,124/1+0,124 = 0,110
Для категорий 0+1, кумулятивно: 0,181/1+0?181=0,153 или для одной категории 1:
0,153 – 0,124 = 0,042.
Анализ компонентов ковариации показывает значимую вариацию оценок по школам.
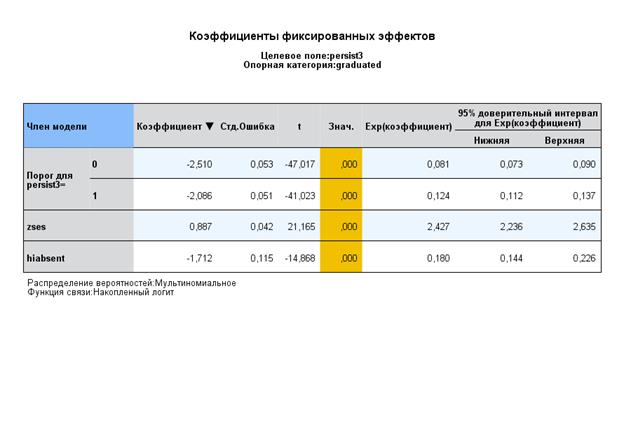
Далее включим в модель два фактора – SES как предиктор школьного уровня и одни индивидуальный – прогулы. Результат:
1) при увеличении SES на 1 сигму, в 2, 427 раза повышается вероятность продолжения обучения,
2) при переходе к прогулам (от 0 к 1) вероятность продолжения обучения всего 0,18 или она снижается на 82%.
Для тех случаем, когда ранги распределены неравномерно – есть маленькие и большие частоты при измерении ЗП, обычно используют кумулятивную дополняющую лог-лог функцию связи.
Важно, что для процедуры GENLINMIXED имеет значение, какой указан уровень измерения ЗП – номинальный или порядковый! Тем не менее, стоит иметь в виду, что мультноминальная модель игнорируют упорядоченность категорий.
Дата: 2019-02-19, просмотров: 389.