Специфика данных – это положительные целые числа и нули.
Если регистрируемые частоты редкие данные – это Пуасоновское распределение, если более частые – нужно использовать как распределение биноминальную негативную модель.
Для Пуасоновского распределения два вида данных – с постоянным интервалом наблюдения (число всех возможных исходов константно), и с переменным – когда для разных наблюдений разный интервал наблюдения (тогда нужно оценивать не абсолютные, а относительные частоты).
Данные – файл ch7data1.sav: 9956 старшеклассников 9 класса из 44 школ.
Как показал Хокс (2001), при выборках небольшого размера не всегда для всех наблюдений среднее совпадает с дисперсией (как положено для Пуасоновского распределения: σ  ), поэтому компенсации этого недостатка следует использовать опцию робастной оценки стандартной ошибки.
), поэтому компенсации этого недостатка следует использовать опцию робастной оценки стандартной ошибки.
Одноуровневые модели.
η i = log ( 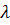 ) = β0
) = β0
Или оценивается к-т, равный натуральному логарифму параметра пуасовновского распределения. В данном случае интерсепт без предикторов интерпретируется как логарифм ожидаемой частоты провала хотя бы одного курса ( 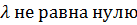 ) первокурсником старшей школы по всей выборке школьников (процедура GENLIN): с вероятностью 0,602 школьник завалит в этом семестре хоть один курс.
) первокурсником старшей школы по всей выборке школьников (процедура GENLIN): с вероятностью 0,602 школьник завалит в этом семестре хоть один курс.
| Параметр | B | Проверка гипотезы | Exp(B) | ||
| Хи-квадрат Вальда | ст.св. | Знч. | |||
| (Константа) | -,508 | 1544,799 | 1 | ,000 | ,602 |
| (Масштаб) | 1a | ||||
Логарифм для распределения Пуасссона – это каноническая функция связи.
Можно также подсчитать по формуле вероятность провала 1, 2, 3 или 4 курсов: 0,33 – 0,099 – 0,02 – 0,003 (с. 332).
Далее включим в модель три фактора: SES, пол, тест по математике и возраст:
η i = log ( 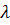 ) = β 0 +SES + male + math +age
) = β 0 +SES + male + math +age
Все факторы укажем как ковариаты:
| Параметр | B | Стд. Ошибка | Проверка гипотезы | Exp(B) | ||
| Хи-квадрат Вальда | ст.св. | Знч. | ||||
| (Константа) | -2,473 | ,5220 | 22,442 | 1 | ,000 | ,084 |
| lowses | ,344 | ,0372 | 85,532 | 1 | ,000 | 1,411 |
| male | ,168 | ,0358 | 21,902 | 1 | ,000 | 1,182 |
| math | -,007 | ,0003 | 611,736 | 1 | ,000 | ,993 |
| age | ,242 | ,0375 | 41,721 | 1 | ,000 | 1,274 |
| (Масштаб) | 1a | |||||
Интерпретация:
- SES: при переходе от 0 к 1 (т.е. к малообеспеченным) на 41% увеличивается вероятность провала курса:
- Male: для мальчиков (1) вероятность на 18% больше,
- чем старше школьник, тем выше вероятность провала: на каждый год по 27%,
- чем выше уровень по математике, тем ниже вероятность провала: на каждую сигму по 0,7%.
Проблема переоценки дисперсии в распределении Пауссона:
- scale-factor по умолчанию устанавливается 1, это правильно при тоной оценке дисперсии;
- хороший показатель оценки дисперсии – отношение дисперсии модели к числу степеней свободы, он д.б. около 1:
| Статистики согласияa | |||
| Значение | ст.св. | Значение/ст.св. | |
| Уклонение | 14322,071 | 9951 | 1,439 |
| Масштабированное уклонение | 14322,071 | 9951 | |
| Хи-квадрат Пирсона | 17971,844 | 9951 | 1,806 |
| Масштабированное значение хи-квадрат Пирсона | 17971,844 | 9951 | |
| Log-правдоподобиеb | -10926,549 | ||
| Информационный критерий Акаике (AIC) | 21863,098 | ||
| Скорректированный информационный критерий Акаике (AICC) для выборки конечного объема | 21863,104 | ||
| Информационный критерий Байеса (BIC) | 21899,127 | ||
| Состоятельный информационный критерий Акаике (CAIC) | 21904,127 | ||
- в случае расхождения можно использовать более общую модель – отрицательное биноминальное распределение (второй вариант обработки данных типа частоты) с логарифмической функцией связи, позволяющую работать с переоценкой дисперсии (Хокс, 2010); в этом случае нужно указать вспомогательный параметр – внизу окна (0 или 1, или что-то еще); сравнить хорошесть подгонки данных под модель можно с помощью 2-х инфоромационных критериев AIC и BIC.
Двухуровневые модели
Используем процедуру GENLIN MIXED, 4 фиксированными факторами и робастным оцениванием коэффициентов – это одноуровневая модель. Объект в данной модели – это школы.
Далее оценим 2-х уровневую необусловленную модель:
η ij = log ( 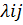 ) = β0 j
) = β0 j
(т.е. с одним интерсептом, варьирующим на уровне школ - 2 –ом уровне):
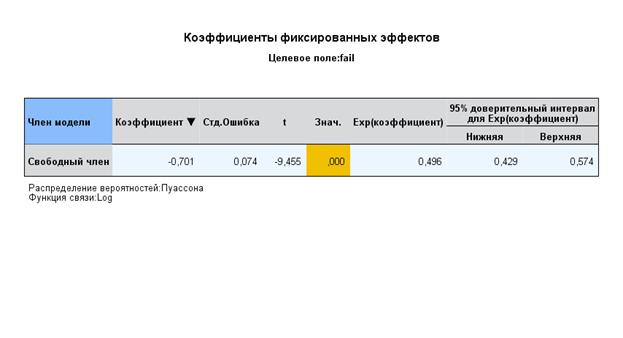
Это означает, что по всем школам вероятность провала курса для учеников – 0,496.
Кроме того, установлена достоверная вероятность вариации (0,220) такой вероятности между школами (изменчивость на втором уровне):

Из этого можно оценить вероятность провала по 1 курсу:
P(Y=1) = (e-0,496)(0,496)/1! = 0,302
Включим в модель фиксированные факторы и рассмотрим их влияние на 2-ом уровне – с учетом вариации по школам:
η ij = log ( 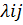 ) = β 0j + b1SES +b2male + b3gmmath + b4gmage
) = β 0j + b1SES +b2male + b3gmmath + b4gmage
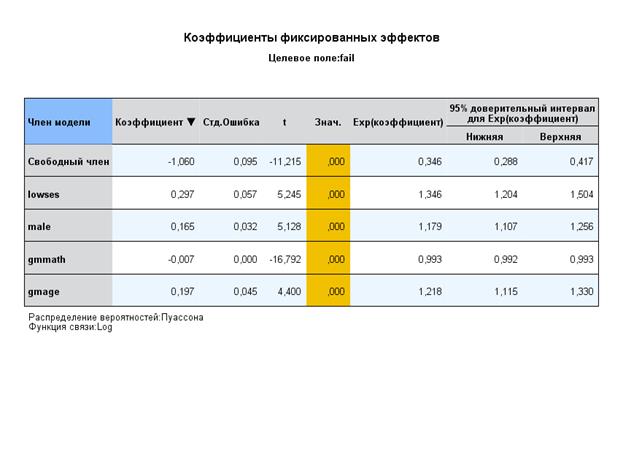 Интерпретация:
Интерпретация:
1. Интерсепт показывает, что средняя девочка со средним или высоким семейным доходом и со средним возрастом и средним рейтингом по математике имеет вероятность завалить курс 0,346.
2. Все предикторы оказывают значимое влияние на ЗП.
3. Дисперсия между школами также значима.
Обработка с помощью отрицательного биноминального распределения дает немного лучшую подгонку.
Включим в модель еще один случайный фактор – SES, и рассмотри его возможную вариацию по школам. Оказалось, что эта вариация не значима:
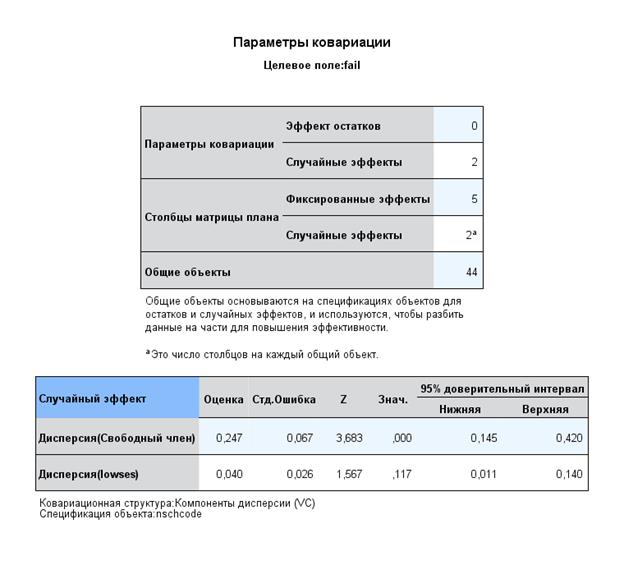
Добавление в модель межуровневые взаимодействия – т.е. одни факторы связаны с уровнем индивидуальности испытуемого, другие – с контекстом самой школы
В модель добавляются два школьных фактора (стаж и наличие лицензии у учителя) и их взаимодействие с SES. Эти факторы обеспечивают новый источник вариации – факторов перового уровня (наклон регрессионной прямой) на втором уровне (разные интерсепты).
Для оценки связи между интерсептом и наклоном, как третьего компонента ковариационной матрицы, выберем тип неструктурированной ковариационной матрицы.
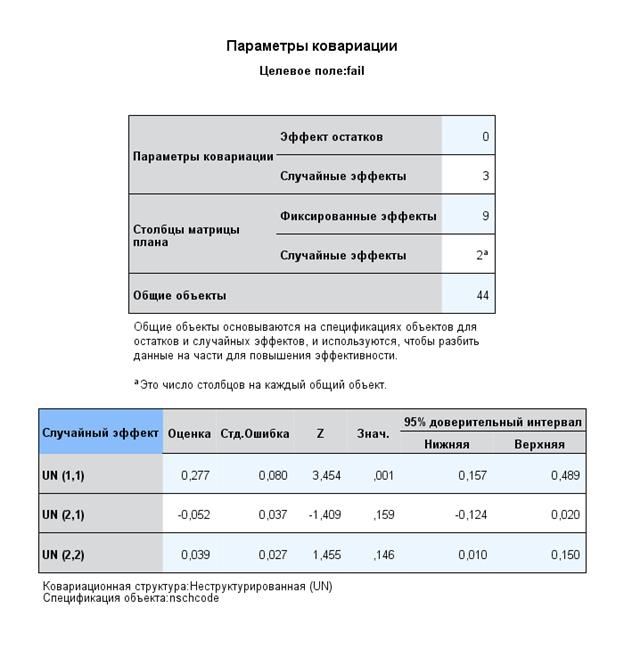
UN (1,1) – вариация интерсептов на втором уровне,
UN (2,1) – вариация факторов 1 и 2 уровней, т.е. наклона и интерсепта,
UN (2,2) – вариация SES на втором уровне.
Дата: 2019-02-19, просмотров: 424.