Проверка эффектов модели
Иcточник
Тип III
Зависимая переменная: readprof
Модель: (Константа), time
|
Оценки параметров | ||||||||||
| Параметр | B | Стд. Ошибка | 95% доверительный интервал Вальда | Проверка гипотезы | Exp(B) | 95% доверительный интервал Вальда для Exp(B) | ||||
| Нижняя | Верхняя | Хи-квадрат Вальда | ст.св. | Знч. | Нижняя | Верхняя | ||||
| (Константа) | ,838 | ,0478 | ,744 | ,931 | 306,910 | 1 | ,000 | 2,311 | 2,104 | 2,538 |
| time | -,055 | ,0165 | -,087 | -,022 | 11,021 | 1 | ,001 | ,947 | ,916 | ,978 |
| (Масштаб) | 1 | |||||||||
| Зависимая переменная: readprof Модель: (Константа), time | ||||||||||
В=0,838 – логарифм odds интерсепта (т.е. опорной категории - 0) – это процент испытуемых в первом (опорном!) измерении, имеющих оценки, отличные от 0. Экспонента в этой степени=2,311 – это означает, что в начале исследования число испытуемых, показавших категорию 1, в 2,311 раза больше, чем категорию 0.
Величина В для ковариаты= -0,055, показывает, что зависимая переменная убывает во времени (0, 1, 2 и 3 – повторные измеренеия) на 5,5% каждый раз.
Можно в модель включать и фиксированные факторы, а также эффекты межфакторных взаимодействий.
Те же модели с повторными измерениями можно строить и используя процедуру GENLIN MIXED. Она дает дополнительную возможность кроме эффектов, рассматриваемых на всей популяции интереса, оценивать многоуровневые модели и влияние вложенных факторов.
Полезно заказать распечатку компонентов дисперсии – для того, чтобы оценить вклад фактора индивидуальных различий. Для этого оценку случайного параметра – интерсепта, делят на его сумму со случайной дисперсии логистического распределения:
В/(В+3,29).
В случае построения 3-х уровневых моделей с повторными измерениями в качестве фактора третьего уровня задаются повторные измерения.
При описании структуры данных в Дополнительно появляются и другие варианты структуры корр. матриц: например, Масштабированная – это означает постоянство дисперсий, но отсутствие корреляций между ее элементами.
Если в моделе всего один й фактор – интерсепт, то при выборе типа ковариации случайных эффектов нужно задать Компоненты дисперсии, что соответствует идентичной ковариационной матрицы для случайного интерсепта.
Изучение медиаторных эффектов в одноуровневых моделях.
Для этого строят две модели: 1) с медиатором и базовым предиктором, а затем – 2) модель, оценивающую зависимость самого предиктора от медиатора; полученные коэффициенты перемножают – это и есть оценка медиаторного эффекта, его значимость оценивают по формуле.
Двухуровневые модели
Используем процедуру GENLIN MIXED, 4 фиксированными факторами и робастным оцениванием коэффициентов – это одноуровневая модель. Объект в данной модели – это школы.
Далее оценим 2-х уровневую необусловленную модель:
η ij = log (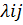 
) = β0 j
(т.е. с одним интерсептом, варьирующим на уровне школ - 2 –ом уровне):
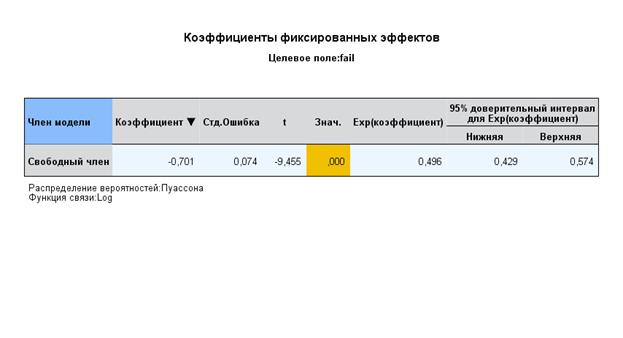
Это означает, что по всем школам вероятность провала курса для учеников – 0,496.
Кроме того, установлена достоверная вероятность вариации (0,220) такой вероятности между школами (изменчивость на втором уровне):
Из этого можно оценить вероятность провала по 1 курсу:
P(Y=1) = (e-0,496)(0,496)/1! = 0,302
Включим в модель фиксированные факторы и рассмотрим их влияние на 2-ом уровне – с учетом вариации по школам:
η ij = log ( 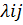) = β 0j + b1SES +b2male + b3gmmath + b4gmage
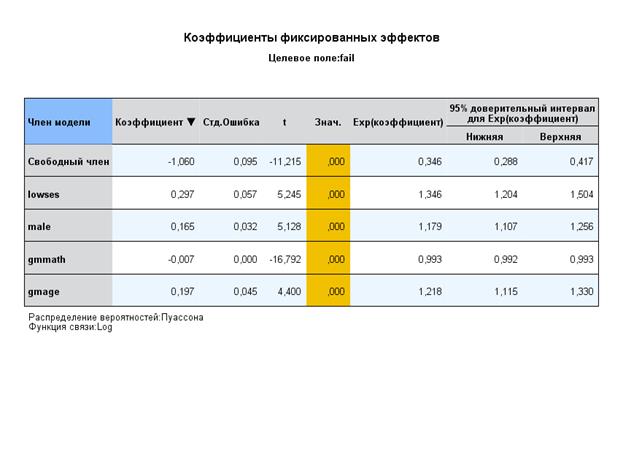Интерпретация:
1. Интерсепт показывает, что средняя девочка со средним или высоким семейным доходом и со средним возрастом и средним рейтингом по математике имеет вероятность завалить курс 0,346.
2. Все предикторы оказывают значимое влияние на ЗП.
3. Дисперсия между школами также значима.
Обработка с помощью отрицательного биноминального распределения дает немного лучшую подгонку.
Включим в модель еще один случайный фактор – SES, и рассмотри его возможную вариацию по школам. Оказалось, что эта вариация не значима:
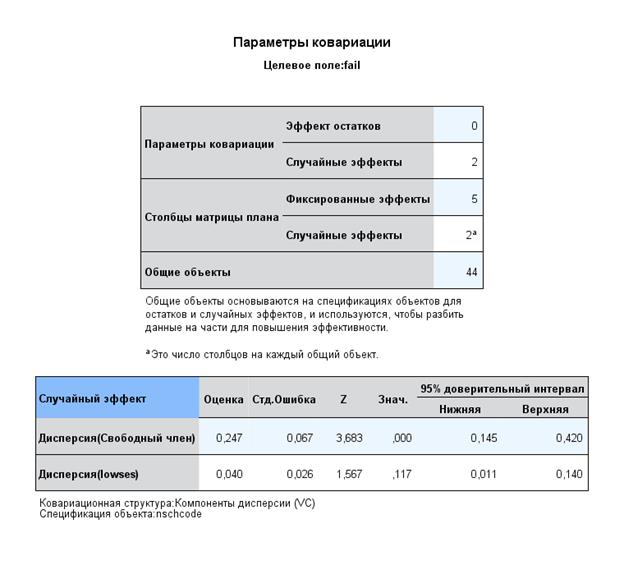
Добавление в модель межуровневые взаимодействия – т.е. одни факторы связаны с уровнем индивидуальности испытуемого, другие – с контекстом самой школы
В модель добавляются два школьных фактора (стаж и наличие лицензии у учителя) и их взаимодействие с SES. Эти факторы обеспечивают новый источник вариации – факторов перового уровня (наклон регрессионной прямой) на втором уровне (разные интерсепты).
Для оценки связи между интерсептом и наклоном, как третьего компонента ковариационной матрицы, выберем тип неструктурированной ковариационной матрицы.
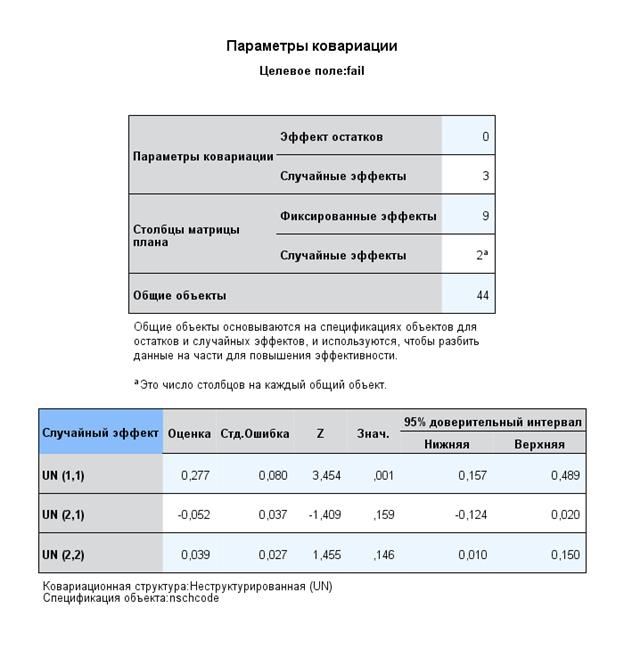
UN (1,1) – вариация интерсептов на втором уровне,
UN (2,1) – вариация факторов 1 и 2 уровней, т.е. наклона и интерсепта,
UN (2,2) – вариация SES на втором уровне.
Глава 3. Обработка одноуровневых моделей.
Используется процедура GENLIN – Обобщенные линейные модели. Предполагается, что испытуемые случайно выбраны из одной совокупности и нет их какой-либо группировки более высокого уровня.
Здесь в соответствии с типом данных нужно выбрать тип модели или самостоятельно указать тип распределение зависимой переменной (ЗП) и вид функции связи (эта функция делает распределение эмпирических оценок линейным).
Для номинальных переменных нужно указать опорную категорию – ту категорию, относительно которой в рамках модели оценивается отношение правдоподобия – вероятность появления данной категории относительно опорной категории.
Если ЗП представляет собой частоту появления некоторого события, то нужно либо указать дополнительную переменную, в которой дано число наблюдений (например, проб в серии) или указать число этих проб.
При определении предикторов можно задать Смещение ( Offset ) – это член регрессионной модели (он не оценивается, по умолчанию = 1, его величина добавляется к линейному предиктору ЗП; полезен в распределении Пуассона), который отражает вес или значимость зависимой переменной (например, два неуда за семестр или за весь курс обучения). В распределении Пуассона эта переменная, в которой задано общее число наблюдений, на котором эмпирически регистрируются частоты интересующих исследователя событий, например, число неудов по курсу в период обучения; в этом случае переменная смещения – это число курсов или число семестров.
В модель можно включать как факторные эффекты, так и межфакторные
Задавая взаимодействия, можно строить нестинг-модели, т.е. когда мы не допускаем взаимодействия одного фактора с другим, и он рассматривается как вложенный.
Во вкладке «Оценивание» можно выбрать метод оценки параметров модели и исходные значения для оценки параметров модели. Выбор Метода включает 3 варианта: расчет по Фишеру, метод Ньютона-Рафсона или гибридный метод (в нем сначала реализуется метод Фишера, а затем другой – в зависимости от сходимости и достижения максимума итераций).
Метод оценки параметра масштаба позволяет сделать выбор из 3-х вариантов: максимальное правдоподобие, фиксированное значение, отклонение, хи-квадрат Пирсона. В зависимости от модели возможны разные методы. Максимальное правдоподобие модели достигается соответствием параметра масштаба и эффектов модели. Важно: эта опция не работает, если имеет место биноминальное, негативно-биноминальное, мультиноминальное или Пуасоновское распределения. При выборе отклонения и хи-квадрата Пирсона параметр масштаба оценивается в соответствии со значениями этих статистик. Можно задать и фиксированное значение этого параметра.
Исходные значения – процедура сама автоматически вычисляет начальные значения параметров модели или они могут быть заданы из файла.
Ковариационная матрица – два варианта оценки параметров вариативности: на основе модели или робастная оценка. В моделях логистической регрессии оценка происходит на основе принципа независимости наблюдений. В случае повторных измерений или кластерной структуры данных при расчете стандартных ошибок робастный метод учитывает зависимость данных. Выбор оценивания на основе модели подходит к данным, предполагающим нормальное распределение и отсутствие кластеризации, когда и среднее, и ковариации определяются точно. При нарушении этих допущений стандатная ошибка переоценивается, поэтому более подходит робастный метод (он же – Хьюбера/Белый/Сандвич), позволяющий скорректировать оценку ковариации даже при несоответствии дисперсии и функции связи. Робастная оценка – не панацея от всех нарушений модели, например, при небольших выбоках может наблюдаться смещение оценок. Поэтому, лучше использовать расчет на основе модели или делать оба варианта.
Статистики – это установки различных эффектов модели и вывода результатов. Эффекты модели включают выбор:
· Типа анализа (или расчет суммы квадратов): 3 типа – 1 (в модели предполагается некоторая упорядоченность предикторов), 3 (применяется чаще всего ) и комбинация 1 и 3.
· Статистики хи-квадрат для проверки модели: два варианта – по Вальду или отношение правдоподобия. Статистики на основе хи-квадрат заменяют обычное оценивание нулевой гипотезы на основе нормального распределения. Тест Вальда сходен с t-тестом, это квадрат z-статистики, и подчиняется распределению хи-квадрат с одной степенью свободы для больших выборок. На малых выборках он не хорош, для них более подходит оценка отношения правдоподобия.
· Функция логорифма отношения правдоподобия – можно менять отображение формата этой функции.
Вкладка «Оценки маргинальных средних» – распечатка групповых и межгрупповых средних (только для количественных данных).
Дата: 2019-02-19, просмотров: 245.
