Используется процедура GENLINMIX – Обобщенные смешанные модели.

Необусловленная или нулевая модель – это модель, включающая вариацию лишь свободного члена - интерсепта (переменной первого или второго уровня), она используется для проверки гипотезы о наличии значимости его вариации между структурными элементами этой переменной как случайного фактора.

Коэффициент = 0, 231 – это оценка натуральный логарифма отношения правдоподобия (log odds), а экспоненциальный коэффициент – это «е» (2,71828) в степени логарифма отношения правдоподобия или отношение odds =1,26, что означает, что женатых испытуемых в среднем по всем категориям переменной второго уровня больше в 1,26.

Оценка дисперсии интерсепта – 0,159 (как величины межгрупповой дисперсии), показывает вероятность того, что имеет или не имеет место его достоверная вариация по уровням случайного фактора – в этом примере индивидуального дохода респондента. По ее величине можно оценить коэффициент интерклассовй корреляции (отношение межгрупповой дисперсии к общей дисперсии – межгрупповая + внутригрупповая – π² /3):

Ρ= 0,159/(0,159 +3,29)=0,0461 , т.е. доля ее вариации составляет 4,6 % от общей вариации быть женатым или неженатым по всем испытуемым.

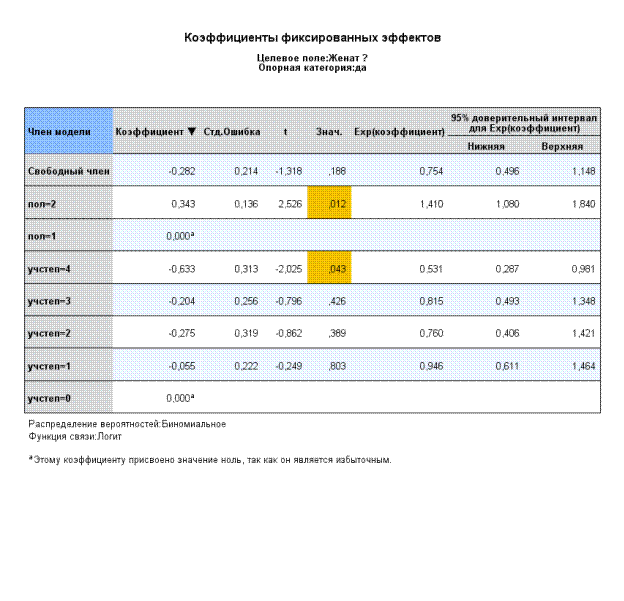
Это оценки факторных эффектов для каждого уровня фиксированного фактора. При определении типа ковариации случайных эффектов задаем опцию по умолчанию - «Компоненты дисперсии».

Если в модели мы задаем лишь интерсепт, то при определении типа ковариации случайных эффектов выбираем «Неструктурированная».

Если в модели нет повторных измерений, а присутствует только один фактор второго порядка, то определяя структуру данных, нужно указать эту порядковую или дихотомическую переменную, которая является для всех первичных переменных (т.е. переменных, структуртурирующих зависимую переменную на первом уровне) более общей, задающей структурирование второго уровня. Например, это может быть список школ или вузов, из которых получены данные по учащимся.

Если мы строим трехуровневую модель, то первым указывается фактор третьего уровня, а затем – второго, как входящий в первый. Например: пол испытуемого – случайный фактор третьего уровня, а возрастная группа – фактор второго уровня. Или: номер школы и класс, или – регион и город, или – национальность и пол, или – профессиональная (социальная) группа и пол.

Для оценки вклада случайных факторов второго или третьего или только второго уровня в модель нужно включать интерсепт соответствующего фактора и их взаимодействия (для 3-х уровневых моделей).

При определении целевой дихотомической категориальной пременной, т.е. зависимой, переменной в качестве вида модели нужно задавать «Бинарная логистическа регрессия». Это соответствует биноминальному распределению и функции связи логит.

При выборе Параметров конструкции целесообразно задавать сортировку по убыванию: в этом случае опорной (референтной) категорией будет наименьшая – при бинарных данных –это исход «0». Поэтому все оценки будут рассчитываться как вероятность возникновения исхода «1» относительно «0». Тоже касается и переменной предиктора – в результатах будет рассчитываться вероятность влияния второй категории 1 относительно 0 или 2 отностительно 1.

Для мультиминальных переменных нужно также определиться – какая переменная будет референтной (т.е. относительно чего будут сделаны расчёты).