Прямая линия, перпендикулярная какой-либо плоскости проекций, называется проецирующей. Прямая l (рис. 15), перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей.

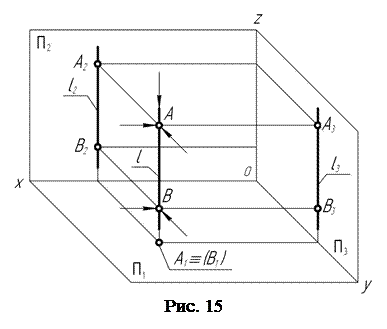Для построения проекций этой прямой на ней выбирают две произвольные точки, например, А и В. Через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций. Отметив точку пересечения проецирующих лучей с соответствующими плоскостями проекций, получают горизонтальные А₁, В₁, фронтальные А₂, В₂ и профильные А₃, В₃ проекции точек А и В, принадлежащих прямой l . Так как прямая l располагается в пространстве перпендикулярно горизонтальной П₁ плоскости проекций, то горизонтальные А₁ и В₁ проекции точек А и В совпадают.

Точки, расположенные на одной проецирующей прямой, называются конкурирующими. С помощью конкурирующих точек устанавливается видимость проекций геометрических фигур на чертеже. Из двух проекций конкурирующих точек видимой является проекция точки, наиболее удаленной от соответствующей плоскости проекций. Точка А наиболее удалена от горизонтальной плоскости проекций, поэтому горизонтальная А₁ проекция точки А является видимой. Горизонтальная В₁ проекция точки В является невидимой, так как она закрывается точкой А. Невидимые проекции точек заключают в круглые скобки.

С горизонтальными проекциями точек А и В совпадает и горизонтальная l₁ проекция прямой l. Соединив прямыми линиями одноименные проекции точек А и В на фронтальной П₂ и профильной П₃ плоскостях проекций, получают фронтальную l₂ и профильную l₃ проекции прямой l.

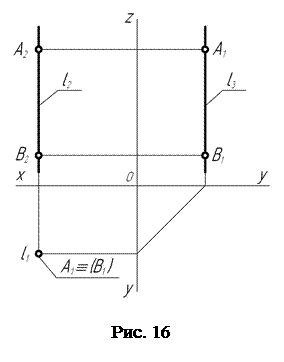
На чертеже (рис. 16) горизонтально проецирующая прямая l выглядит следующим образом: горизонтальная l₁ проекция прямой представляет собой точку, тогда как фронтальная l₂ и профильная l₃ проекции прямой располагаются перпендикулярно соответственно осям проекций Х и Y. Такое расположение на чертеже проекций горизонтально проецирующей прямой и является ее эпюрным признаком.

Так как горизонтально-проецирующая прямая располагается параллельно фронтальной и профильной плоскостям проекций, то на них она проецируется в натуральную величину.

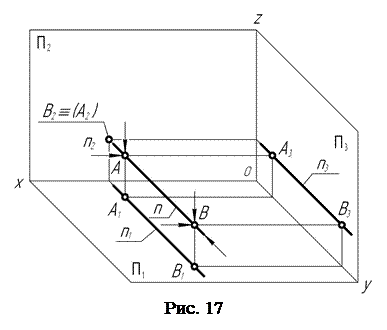
Прямая n (рис. 17), перпендикулярная фронтальной П₂ плоскости проекций, называется фронтально-проецирующей.

Для построения проекций этой прямой на ней выбирают две произвольные точки, например, А и В. Через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций. Отметив точки пересечения проецирующих лучей с плоскостями проекций, получают горизонтальные, профильные и фронтальные проекции точек А и В, принадлежащих прямой n.

Так как прямая n перпендикулярна фронтальной П₂ плоскости проекций, то фронтальные А₂ и В₂ проекции точек совпадают. С этими проекциями точек А и В совпадает и фронтальная n₂ проекция прямой n.

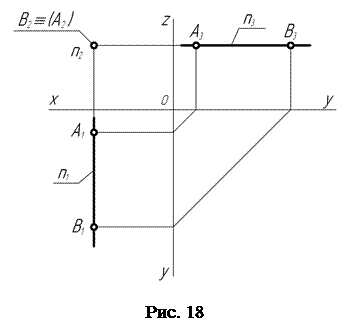
На чертеже (рис. 18) фронтально-проецирующая прямая n выглядит следующим образом: горизонтальная n₁ и профильная n₃ проекции располагаются перпендикулярно соответственно осям проекций Х и Z. Фронтальная n₂ проекция прямой представляет собой точку. Эти особенности расположения проекций фронтально-проецирующей прямой и составляет ее эпюрный признак. Так как фронтально-проецирующая прямая располагается в пространстве параллельно горизонтальной и профильной плоскостям проекций, то на них она проецируется в натуральную величину.

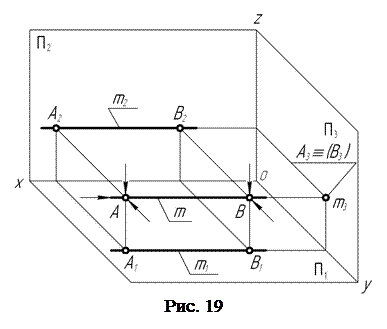
Прямая m (рис. 19), перпендикулярная профильной плоскости проекций, называется профильно-проецирующей.

Для построения проекций этой прямой на ней выбирают две произвольные точки и через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций.

Отметив положения точек пересечения проецирующих лучей с плоскостями проекций, получают горизонтальные, фронтальные и профильные проекции точек А и В, принадлежащих прямой m. Так как прямая m перпендикулярна профильной плоскости проекций, то профильные А₃ и В₃ проекции точек совпадают. С профильными проекциями точек А и В совпадает и профильная m₃ проекция прямой m. Соединив одноименные проекции точек А и В на горизонтальной и фронтальной плоскостях проекций, получают горизонтальную m₁ и фронтальную m₂ проекции прямой m.

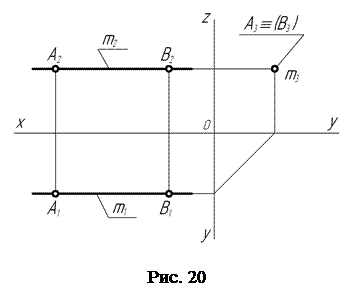
На чертеже (рис. 20) профильно-проецирующая прямая m выглядит следующим образом: профильная m₃ проекция прямой представляет собой точку, а горизонтальная m₁ и фронтальная m₂ проекции прямой располагаются параллельно оси проекций Х. Такое расположение на чертеже проекций профильно-проецирующей прямой и составляет эпюрный признак этой прямой.

Вопросы для самопроверки

1. Какое положение в пространстве занимает прямая общего положения относительно заданной системы плоскостей проекций?

2. Сколько точек прямой однозначно определяют ее положение в пространстве и почему?

3. Каким образом строят проекции произвольной прямой общего положения?

4. В чем состоит эпюрный (чертежный) признак прямой общего положения?

5. Каким образом по чертежу прямой общего положения можно построить ее наглядное изображение – аксонометрическую проекцию?

6. Какие прямые занимают в пространстве частные положения относительно заданной системы плоскостей проекций?

7. Какое положение относительно плоскостей проекций занимает прямая уровня?

8. На какую из плоскостей проекций прямая уровня проецируется в натуральную величину?

9. Какое положение относительно плоскостей проекций занимает горизонтальная прямая?

10. В чем состоит эпюрный признак горизонтальной прямой?

11. На какой плоскости проекций и каким образом определяется натуральная величина угла наклона горизонтальной прямой к фронтальной или профильной плоскостям проекций?

12. Какое значение угла наклона не может иметь горизонтальная прямая по отношению к фронтальной и профильной плоскостям проекций?

13. Какое положение относительно плоскостей проекций занимает фронтальная прямая?

14. В чем состоит эпюрный признак фронтальной прямой?

15. В чем состоит эпюрный признак профильной прямой?

16. Какое положение относительно плоскостей проекций занимает проецирующая прямая?

17. В чем состоит эпюрный признак горизонтально-, фронтально- или профильно-проецирующей прямой?

18. Какие точки прямой называются конкурирующими? Каким образом определяется видимость проекций конкурирующих точек и как обозначаются на чертеже невидимые проекции точек?