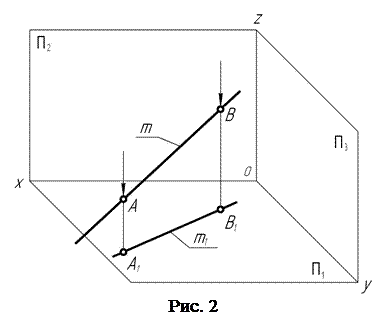
Вначале через точки А и В (рис. 2) проводят проецирующие лучи в направлении, перпендикулярном горизонтальной П₁ плоскости проекций, и отмечают точки А₁ и В₁ пересечения соответствующих лучей с горизонтальной плоскостью проекций.

Соединив точки А₁ и В₁ прямой, получают горизонтальную m₁ проекцию прямой m .

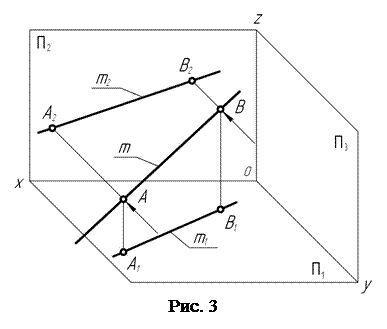Затем (рис. 3) через точки А и В проводят проецирующие лучи в направлении, перпендикулярном фронтальной П₂ плоскости проекций. Отмечают точки А₂ и В₂ пересечения соответствующих проецирующих лучей с фронтальной плоскостью проекций.

Соединив точки А₂ и В₂ прямой, получают фронтальную m₂ проекцию прямой m.

Для построения профильной m ₃ проекции прямой через точки А и В проводят проецирующие лучи в направлении, перпендикулярном профильной П₃ плоскости проекций (рис. 4). Отмечают через точки А₃  и В₃ пересечения соответствующих проецирующих лучей с профильной плоскостью проекций.

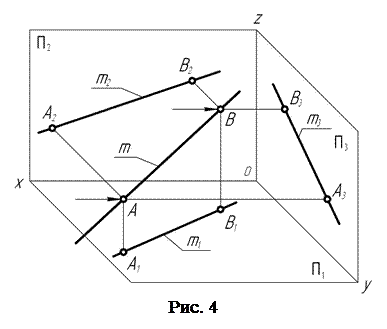Соединив точки А₃ и В₃ прямой, получают профильную m₃ проекцию прямой m.

Строят (рис. 5) проекции отрезков проецирующих лучей АА₁, АА₂, АА₃, ВВ₁, ВВ₂, ВВ₃ на каждую из плоскостей проекций.

Проекции этих отрезков являются линиями связи, соединяющими разноименные проекции точек А и В.

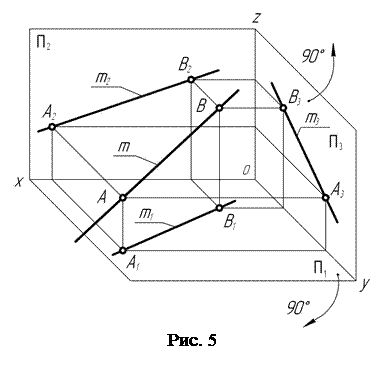Для получения изображения, выполненного в одной плоскости, поворачивают на 90° профильную П₃ плоскость проекций вокруг оси Z, а горизонтальную П₁ плоскость проекций – вокруг оси Х и получают трехкартинный комплексный чертеж (рис. 6).

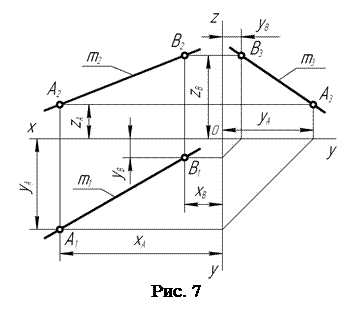
На чертеже линии, соединяющие разноименные проекции точек А и В, например, А₁-А₂, А₂-А₃, А₁-А₃, В₁-В₂, В₂-В₃, В₁-В₃, называются линиями связи. Они располагаются перпендикулярно соответствующим осям проекций. Оси проекций Х, Y и Z образуют прямоугольную систему координат с точкой О – начало отсчета.

Из анализа расположения проекций m₁, m₂, m₃ прямой m относительно осей проекций Х, Y и Z следует, что ни одна из проекций прямой m не параллельна и не перпендикулярна ни одной из осей проекций.

Такое положение проекций прямой на чертеже свидетельствует о том, что в пространстве прямая m не параллельна и не перпендикулярна ни одной из плоскостей проекций, т. е. занимает положение прямой общего положения. Непараллельность и неперпендикулярность проекций прямой ни одной из осей проекций является чертежным (эпюрным) признаком прямой общего положения.

Рассматриваемый (рис. 7) чертеж прямой m (m₁, m₂, m₃) общего положения, выполненный методом прямоугольного проецирования, является не только вполне определенным, но и обратимым, т.е. по нему можно сконструировать положение (иначе – построить наглядное изображение) прямой m пространства относительно заданной системы трех взаимно перпендикулярных плоскостей проекций: горизонтальной, фронтальной и профильной.

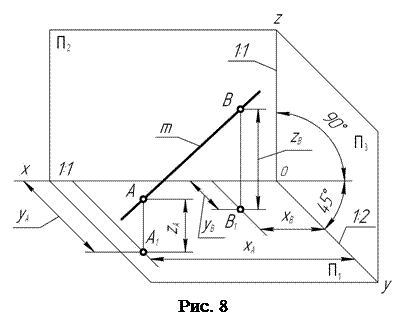
Для этого по чертежу измеряют в определенном масштабе (например, в мм) координаты точек: А (Х_А, Y_А, Z_А) и В (Х_В, Y_В, Z_В). Строят (рис. 8) наглядное изображение – аксонометрическую проекцию (например, косоугольную фронтальную диметрию) системы трех взаимно перпендикулярных плоскостей проекций П₁, П₂, П₃ с коэффициентами искажения по аксонометрическим осям Х и Z, равным 1, а по оси Y – 0,5.

Вначале по оси Х в масштабе 1:1 откладывают абсциссы Х_А и Х_В и проводят прямые линии в плоскости ХОY параллельно оси Y.

На этих прямых в масштабе 1:2 откладывают соответствующие ординаты Y_А и Y_В. В результате получают горизонтальные А₁ и В₁ проекции точек А и В.

Затем из точек А₁ и В₁ проводят прямые линии в направлении, параллельном оси проекций Z, и на них в масштабе 1:1 откладывают соответствующие аппликаты Z_А и Z_В. Получают точки А и В пространства. И, наконец, соединив точки А и В пространства прямой линией, получают прямую m пространства, расположенную не параллельно и не перпендикулярно ни одной из плоскостей проекций, т. е. прямую общего положения.

Рассматривая трехкартинный комплексный чертеж прямой общего положения (рис. 7), необходимо сделать следующие выводы: во-первых, положение проекций прямой на чертеже однозначно определяется положением проекций двух ее произвольных точек; во-вторых, если точка принадлежит прямой, то проекции этой точки должны располагаться на соответствующих проекциях прямой. Последнее положение является эпюрным признаком принадлежности точки прямой.