Прямая линия, расположенная в пространстве параллельно какой-либо плоскости проекций, называется прямой уровня. Все точки этой прямой находятся на одинаковом уровне (одинаковом расстоянии) от параллельной ей плоскости проекций. Прямая уровня проецируется на параллельную ей плоскость проекций в натуральную величину. Прямая h, параллельная горизонтальной плоскости проекций, называется горизонталью.

Для построения проекций горизонтали h (рис. 9) выбирают две произвольные точки, например А и В, ей принадлежащие. Через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций П₁ и П₂.

Отметив точки пересечения проецирующих лучей в с соответствующими плоскостями проекций, получают горизонтальные А₁ и В₁ и фронтальные А₂ и В₂ проекции точек А и В. Соединив прямой линией одноименные проекции точек А и В, получают горизонтальную h₁ и фронтальную h₂  проекции горизонтали.

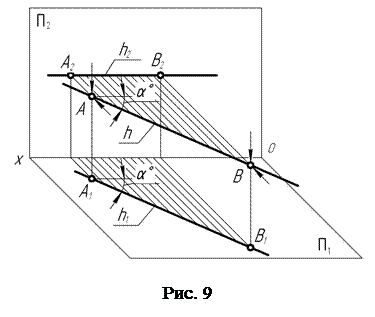Если теперь в плоскости АА₂В₂В провести через точку А прямую, параллельную А₂В₂, то угол, образованный этой прямой и прямой h, представляет собой натуральную величину угла наклона горизонтали к фронтальной плоскости проекций.

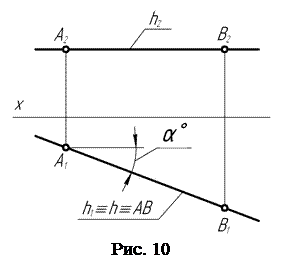
Двухкартинный комплексный чертеж горизонтали h выглядит следующим образом (рис. 10): так как все точки горизонтальной прямой расположены на одинаковом расстоянии от горизонтальной П₁ плоскости проекций, то ее фронтальная h₂ проекция располагается параллельно оси Х.

Параллельность фронтальной h₂  проекции оси Х является эпюрным признаком горизонтальной прямой.

Расстояние фронтальной h₂ проекции до оси Х есть возвышение прямой над горизонтальной П₁ плоскостью проекций.

На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину. Угол наклона горизонтальной h₁ проекции горизонтали к оси Х есть натуральная величина угла наклона горизонтальной прямой h в пространстве к фронтальной плоскости проекций.

Прямая f, расположенная в пространстве параллельно фронтальной плоскости проекций, называется фронтальной прямой (фронталью).

Для построения проекций прямой f (рис. 11) на ней выбирают две произвольные точки, например, А и В, и через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций П₁ и П₂. Отметив положения точек пересечения проецирующих лучей с соответствующими плоскостями проекций, получают горизонтальные А₁ и В₁, фронтальные А₂ и В₂, проекции выбранных точек. Соединив одноименные проекции точек А и В прямыми, получают горизонтальную f₁  и фронтальную f₂  проекции прямой f .

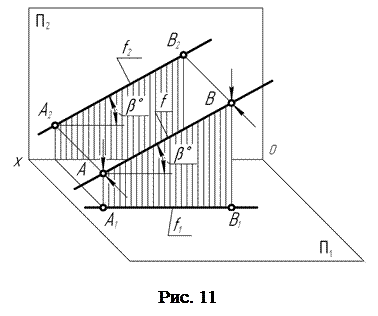Если теперь в плоскости АА₁В₁В через точку А провести прямую, параллельную А₁В₁, то угол, образованный этой прямой и прямой f , будет представлять собой натуральную величину угла наклона фронтали f к горизонтальной П₁  плоскости проекций.

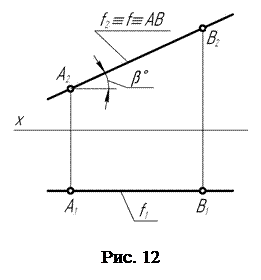
Двухкартинный комплексный чертеж фронтали f (рис. 12) выглядит следующим образом: горизонтальная f₁  проекция фронтали располагается параллельно оси проекций Х, так как все точки фронтальной прямой одинаково удалены от фронтальной П₂ плоскости проекций.

Параллельность горизонтальной f₁ проекции фронтали оси проекций Х и является эпюрным признаком фронтальной прямой. На фронтальную плоскость проекции фронталь проецируется в натуральную величину.

Угол наклона фронтальной f₁ проекции фронтали и оси проекций есть натуральная величина угла наклона фронтальной прямой пространства к горизонтальной П₁ плоскости проекций.

Прямая р (рис. 13), расположенная в пространстве параллельно профильной П₃ плоскости проекций, называется профильной. Для построения проекций этой прямой на ней выбирают две произвольные точки, например, А и В. Через них проводят проецирующие лучи в направлениях, перпендикулярных плоскостям проекций. Отметив точки пересечения проецирующих лучей с соответствующими плоскостями проекций, получают горизонтальные А₁, В₁, фронтальные А₂, В₂ и профильные А₃, В₃ проекции точек А и В, принадлежащих прямой р.

Соединив одноименные проекции точек А и В прямыми, получают горизонтальную р₁, фронтальную р₂, профильную р₃ проекции профильной прямой  р.

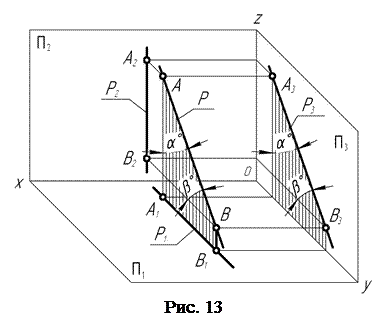Если в плоскости АА₂В₂В через точку А и в плоскости АА₁В₁В через точку провести прямые, параллельные соответственно А₂В₂ и А₁В₁, то углы, образованные этими прямыми с прямой р, представляют собой натуральную величину углов наклона профильной прямой р к фронтальной и горизонтальной плоскостям проекций. И так как плоскости АА₂В₂В и АА₁В₁В параллельны профильной плоскости проекций, то на нее углы наклона профильной прямой р к фронтальной П₂ и горизонтальной П₁ плоскостям проекций спроецируются в натуральную величину.

Трехкартинный комплексный чертеж профильной прямой (рис. 14) выглядит следующим образом: фронтальная р₂ и горизонтальная р₁ проекции прямой располагаются перпендикулярно оси проекций Х, так как все точки профильной прямой одинаково удалены от профильной плоскости проекций. Это обстоятельство и является эпюрным признаком профильной прямой.

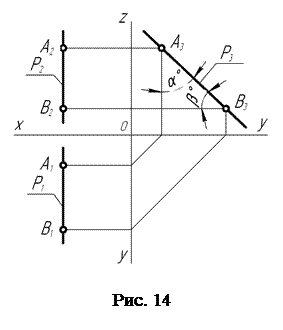Расстояние горизонтальной р₁ проекции прямой до оси проекций Y и фронтальной р₂ проекции прямой до оси проекций Z есть удаление прямой р пространства от профильной плоскости проекций. На профильную плоскость проекций профильная прямая проецируется в натуральную величину. Углы, образованные профильной р₃ проекцией прямой с осями проекций Z и Y, представляют собой натуральные величины углов наклона профильной прямой р соответственно к фронтальной и горизонтальной плоскостям проекций.