Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Ю.А. Зайцев

 

 

Начертательная геометрия.

 

РЕШЕНИЕ ЗАДАЧ

 

 

Рекомендовано

научно-методическим советом по начертательной геометрии, инженерной и компьютерной графике Министерства образования и науки РФ в качестве учебного пособия для студентов технических специальностей вузов

 

 

Саратов – 2008

УДК 515.6

ББК 3-17

К65

 

Рецензенты:

Доктор технических наук, профессор Якунин В.И.
Московского государственного технического университета (МАИ)

Доктор технических наук, профессор Горшков Г.Ф.
Московского государственного института радиотехники, электроники и автоматики (технического университета)

 

 

Одобрено

редакционно-издательским советом
Саратовского государственного технического университета

 

 

Зайцев Ю.А.

Начертательная геометрия. Решение задач: учеб. пособие /
Ю.А. Зайцев. Саратов: Сарат. гос. техн. ун-т, 2007. 242 с.

ISBN 978-5-7433-

 

 

Содержит … чертежи и рисунки, довольно подробно иллюстрирующие динамику выполнения построений графического решения типовых задач.

 

Предназначается для студентов машиностроительных специальностей. В учебном пособии рассматриваются основные теоретические положения курса начертательной геометрии, применяемые в практике графического решения метрических и позиционных задач. При изложении теоретических положений использована методика преподавания курса в Саратовском государственном техническом университете.

 

 

УДК 515.6

ББК 3-17

 

  Ó Саратовский государственный

технический университет, 2007

ISBN 978-5-7433-                                           Ó Зайцев Ю.А., 2007

Введение

Студенты, изучающие курс начертательной геометрии, зачастую испытывают значительные затруднения не только в освоении теоретического курса, но и в практике решения типовых метрических и позиционных задач.

Это объясняется, с одной стороны, пробелами в школьной графической подготовке, а, с другой стороны, рисунки, поясняющие те или иные теоретические или графические решения конкретных задач, являются лишь конечным результатом выполнения целого ряда построений, последовательность выполнения которых довольно трудно проследить от начала до конца.

Целью настоящего учебного пособия является систематизация основных теоретических положений курса начертательной геометрии, соответствующих рабочей программе для студентов технических специальностей очной и заочной формы обучения, представление рекомендаций в практике выполнения построений при графическом решении типовых задач.

Начертательная геометрия способствует развитию у студентов пространственного воображения, без которого сдерживается получение оптимальных решений при проектировании. При конструировании сложных технических поверхностей методы начертательной геометрии позволяют получать рациональные изображения изделий.

Учебное пособие содержит конспекты лекций с вопросами для самопроверки по основным разделам курса начертательной геометрии и примеры выполнения построений графического решения типовых задач. Чертежи и рисунки пособия довольно подробно иллюстрирует динамику выполнения графических построений, что, несомненно, будет способствовать более глубокому усвоению студентами основного теоретического материала курса и значительно облегчит им практику графического решения задач по начертательной геометрии.

Более детальное ознакомление с теми или иными теоретическими положениями или доказательствами курса начертательной геометрии можно получить из источников, указанных в перечне рекомендуемой литературы.

Автор приносит искреннюю благодарность профессорам: В.С. Полозову, В.И. Якунину, Г.С. Иванову, Г.Ф. Горшкову; доцентам: А.Н. Кравцову, В.С. Потоцкому за замечания и советы, направленные на улучшение содержания учебного пособия.

 

ПРЯМОЙ И ПЛОСКОСТИ

Прямая линия и плоскость являются одними из основных геометрических фигур, образующих поверхности большинства деталей машин и приборов.

При построении проекционных чертежей различного рода деталей довольно часто приходится решать метрические и позиционные задачи, связанные с определением как натуральных (истинных) величин отрезков прямых и граней (плоскостей) поверхности детали, углов их наклона относительно друг друга, так и их взаимного расположения.

Для успешного решения этих задач немаловажное значение имеет установление характера расположения в пространстве прямой линии и плоскости относительно друг друга и заданной системы плоскостей проекций по их комплексным чертежам. Такой анализ позволяет проводить операции графического решения задач в определенной последовательности.

 

Общие сведения

 

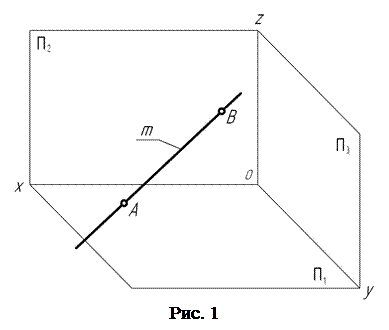Рассматривая положение прямой линии в пространстве (рис. 1) относительно заданной системы плоскостей проекций: горизонтальной – П₁, фронтальной – П₂, профильной – П₃, выделяют прежде всего особые (частные) положения, в которых прямая либо параллельна, либо перпендикулярна какой-либо плоскости проекций.

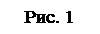Прямую линию, расположенную в пространстве таким образом, что она не параллельна и не перпендикулярна ни одной из плоскостей проекций, называют прямой общего положения.

Положение прямой m относительно заданной системы плоскостей проекций однозначно определяется положением двух ее произвольных (случайных) точек, например, точек А и В. Этот вывод сделан на основе аксиомы сочетания: через каждые две точки можно провести прямую и притом только одну. Тогда для построения горизонтальной m₁, фронтальной m₂ и профильной m₃ проекций прямой m достаточно построить методом прямоугольного (ортогонального) проецирования горизонтальные, фронтальные и профильные проекции точек А и В.

 

Вопросы для самопроверки

 

1. Какое положение в пространстве занимает прямая общего положения относительно заданной системы плоскостей проекций?

2. Сколько точек прямой однозначно определяют ее положение в пространстве и почему?

3. Каким образом строят проекции произвольной прямой общего положения?

4. В чем состоит эпюрный (чертежный) признак прямой общего положения?

5. Каким образом по чертежу прямой общего положения можно построить ее наглядное изображение – аксонометрическую проекцию?

6. Какие прямые занимают в пространстве частные положения относительно заданной системы плоскостей проекций?

7. Какое положение относительно плоскостей проекций занимает прямая уровня?

8. На какую из плоскостей проекций прямая уровня проецируется в натуральную величину?

9. Какое положение относительно плоскостей проекций занимает горизонтальная прямая?

10. В чем состоит эпюрный признак горизонтальной прямой?

11. На какой плоскости проекций и каким образом определяется натуральная величина угла наклона горизонтальной прямой к фронтальной или профильной плоскостям проекций?

12. Какое значение угла наклона не может иметь горизонтальная прямая по отношению к фронтальной и профильной плоскостям проекций?

13. Какое положение относительно плоскостей проекций занимает фронтальная прямая?

14. В чем состоит эпюрный признак фронтальной прямой?

15. В чем состоит эпюрный признак профильной прямой?

16. Какое положение относительно плоскостей проекций занимает проецирующая прямая?

17. В чем состоит эпюрный признак горизонтально-, фронтально- или профильно-проецирующей прямой?

18. Какие точки прямой называются конкурирующими? Каким образом определяется видимость проекций конкурирующих точек и как обозначаются на чертеже невидимые проекции точек?

Проецирующие плоскости

 

Плоскость, перпендикулярная какой-либо плоскости проекций, называют проецирующей. Если плоскость перпендикулярна горизонтальной П_I плоскости проекций, она называется горизонтально-проецирующей (рис. 25, а).

Точки, лежащие в горизонтально-проецирующей плоскости, проецируются на горизонтальную плоскость проекции в прямую линию, которая является горизонтальным следом этой плоскости. Таким образом, след проецирующей плоскости как бы «собирает на себя» проекции геометрических фигур, расположенных в этой плоскости.

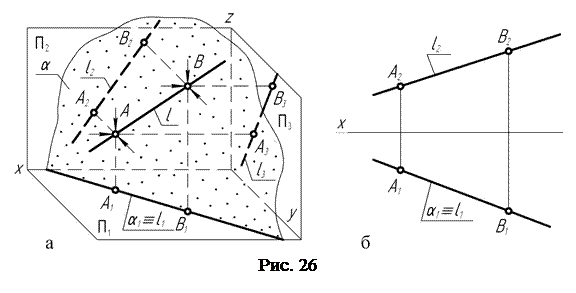
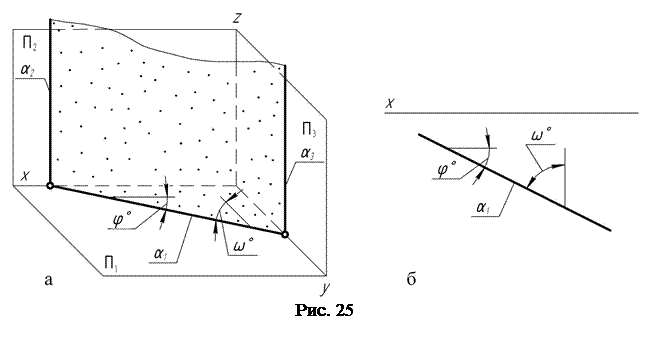«Собирательное» свойство проецирующих плоскостей широко используется для решения целого ряда метрических и позиционных задач. Положение горизонтально-проецирующей плоскости на чертеже вполне однозначно определяется положением горизонтального следа этой плоскости, так как на горизонтальной плоскости проекций можно измерить натуральные величины углов наклона ее к фронтальной и профильной плоскостям проекций. Поэтому на комплексном чертеже (рис. 25, б) горизонтально-проецирующая плоскость a задается только одним своим горизонтальным a₁  следом.

Горизонтальная проекция любой геометрической фигуры, например, прямой l (рис. 26, а), лежащей в горизонтально-проецирующей плоскости a, совпадает с горизонтальным a₁ следом этой плоскости. На фронтальную и профильную плоскости проекций прямая l проецируется с искажением, так как проецирующая плоскость a наклонена к ним под некоторыми углами.

На рис. 26, б представлен комплексный чертеж прямой l, лежащей в горизонтально-проецирующей плоскости a.

Плоскость, перпендикулярную фронтальной П₂ плоскости проекций, называют фронтально-проецирующей (рис. 27, а), эта плоскость проецируется на фронтальную плоскость проекций в прямую линию, являющуюся фронтальным следом плоскости.

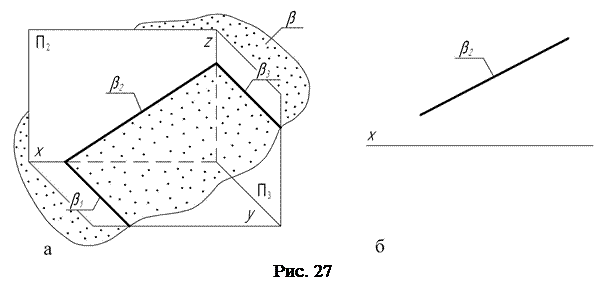Положение фронтально-проецирующей плоскости вполне однозначно определяется положением фронтального следа этой плоскости, так как на фронтальной П₂ плоскости проекций можно измерить натуральные величины углов наклона этой плоскости к горизонтальной и профильной плоскостям проекций.

На комплексном чертеже (рис. 27, б) фронтально-проецирующая плоскость β задается только одним своим фронтальным β₂ следом.

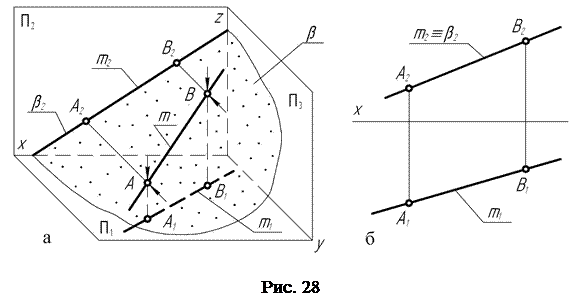
Фронтальная проекция любой геометрической фигуры, например, прямой  m (рис. 28, а), лежащей во фронтально-проецирующей плоскости β, совпадает с фронтальным β₂ следом этой плоскости.

На горизонтальную П_I и профильную П₃ плоскости проекций прямая m проецируется с искажением, так как проецирующая плоскость наклонена к ним под некоторыми углами.

На рис. 28, б представлен комплексный чертеж прямой m, лежащей во фронтально-проецирующей плоскости β.

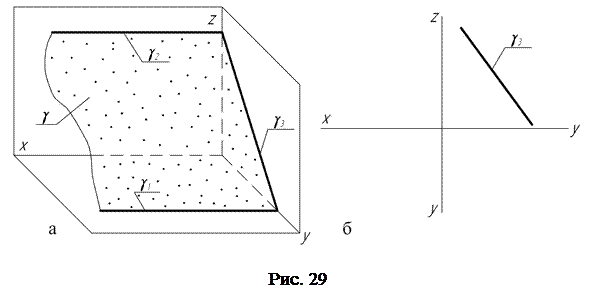Плоскость, перпендикулярную профильной П₃ плоскости проекций, называют профильно-проецирующей. Эта плоскость (рис. 29, а) проецирует все свои точки на профильную плоскость проекций в одну прямую линию, являющуюся профильным следом плоскости.

Положение профильно-проецирующей плоскости вполне однозначно определяется положением профильного следа этой плоскости, так как на профильной плоскости проекций можно измерить натуральные величины углов наклона ее к фронтальной П₂ и горизонтальной П₁ плоскостям проекций.

На комплексном чертеже (рис. 29, б) профильно-проецирующая плоскость γ  задаётся своим профильным g₃ следом.

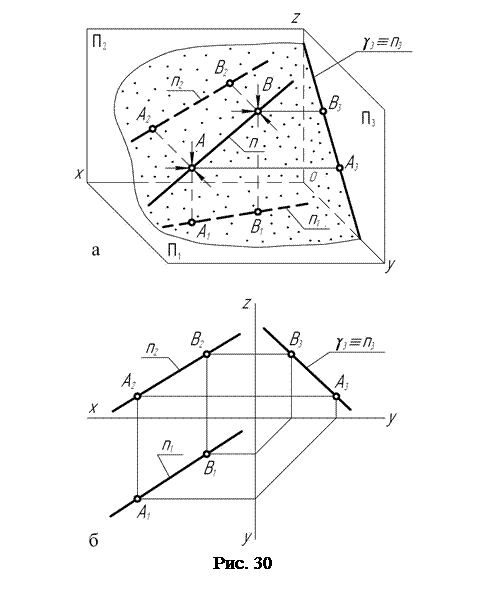
Профильная проекция любой геометрической фигуры, например, прямой n (рис. 30, а), лежащей в профильно-проецирующей плоскости γ, совпадает с профильным γ₃ следом этой плоскости.

На горизонтальную П₁ и на фронтальную П₂  плоскости проекций прямая n проецируется с искажением, так как проецирующая плоскость g наклонена к ним под некоторыми углами.

На рис. 30, б представлен комплексный чертёж прямой n, лежащей в профильно-проецирующей плоскости g.

 

Плоскости уровня

Плоскость, параллельную какой-либо плоскости проекций, называют плоскостью уровня. Все точки этой плоскости одинаково удалены от той плоскости проекций, которой она параллельна. Любая геометрическая фигура, лежащая в плоскости уровня, проецируется на параллельную ей плоскость проекций в натуральную величину.

В системе трёх взаимно перпендикулярных плоскостей проекций плоскость уровня, параллельная одной из них, является одновременно проецирующей по отношению к двум другим. Поэтому на комплексном чертеже плоскость уровня задаётся следом на плоскости проекций, по отношению к которой является проецирующей.

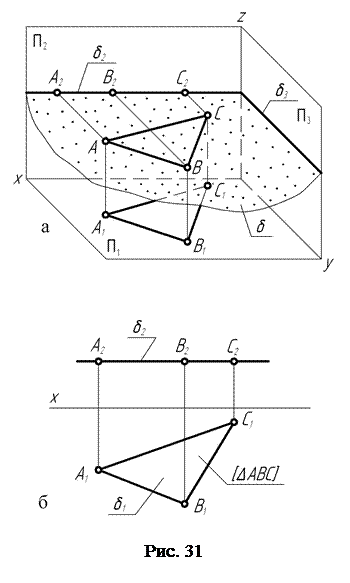Плоскость, параллельную горизонтальной П₁ плоскости проекций, называют горизонтальной плоскостью (рис. 31, а). Любая геометрическая фигура, лежащая в горизонтальной плоскости, например, в плоскости d, проецируется на горизонтальную плоскость проекций без искажения, т.е. в натуральную величину.

Фронтальный d₂ и профильный d₃ следы горизонтальной плоскости d располагаются соответственно параллельно осям проекций X и Y.

На рис. 31, б представлен чертёж горизонтальной плоскости, в которой лежит треугольник ABC. На горизонтальную плоскость проекций он проецируется в натуральную величину.

Плоскость, параллельную фронтальной П₂ плоскости проекций, называют фронтальной (рис. 32, а).

Любая геометрическая фигура, лежащая во фронтальной плоскости, проецируется на фронтальную плоскость проекций в натуральную величину.

Горизонтальный h₁ и профильный h₃  следы фронтальной плоскости располагаются параллельно соответственно осями проекций X и Z.

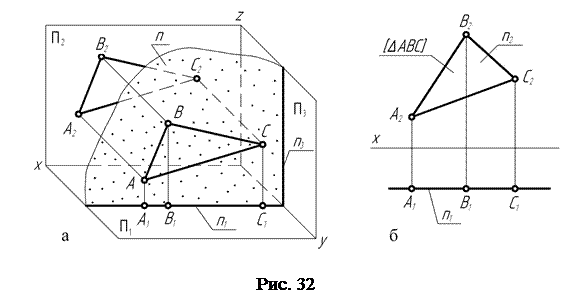На рис. 32, б представлен комплексный чертёж фронтальной плоскости h, в которой лежит треугольник ABC. На фронтальную плоскость проекций он проецируется в натуральную величину. Горизонтальная A₁B₁C₁ проекция треугольника совпадает с горизонтальным следом h₁ плоскости.

Плоскость, параллельную профильной П₃ плоскости проекций, называют профильной (рис. 33, а).

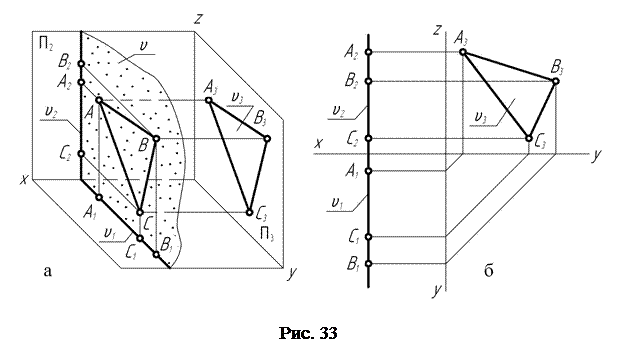Всякая геометрическая фигура, лежащая в профильной плоскости, проецируется на П₃  без искажения в натуральную величину.

Фронтальный u₂  и горизонтальный u₁ следы профильной плоскости u располагаются перпендикулярно оси проекций X.

На рис. 33, б представлен комплексный чертёж профильной плоскости u, в которой лежит треугольник ABC. На профильную плоскость проекций он проецируется в натуральную величину.

 

Плоскости общего положения

 

Плоскость, не перпендикулярную и не параллельную ни одной из плоскостей проекций, называют плоскостью общего положения (рис. 34).

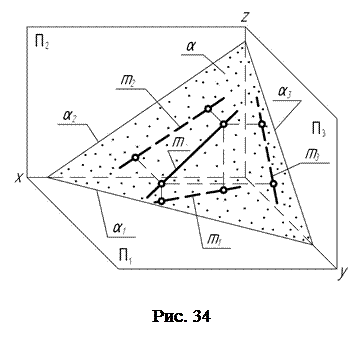Плоскость общего положения пересекает каждую из осей проекций X, Y, Z. Следы плоскости общего положения не параллельны и не перпендикулярны ни одной из осей проекций.

Всякая геометрическая фигура, например прямая m, лежащая в плоскости общего положения, проецируется на любую из плоскостей с искажением.

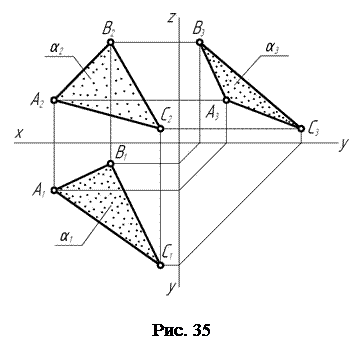На рис. 35 представлен комплексный чертёж плоскости общего положения, заданной треугольником ABC. На любую из плоскостей проекций он проецируется с искажением.

Вопросы для самопроверки

 

1. На основании какой аксиомы определяется положение плоскости в пространстве?

2. Перечислите способы задания плоскости на чертеже.

3. Что называется следом плоскости?

4. Какие положения может занимать плоскость относительно плоскостей проекции?

5. Какую плоскость называют проецирующей?

6. Каким свойством обладают проецирующие плоскости?

7. Изобразите чертёж произвольной горизонтально-проецирующей плоскости, заданной прямой и точкой.

8. Как измерить натуральную величину углов наклона горизонтально-проецирующей плоскости к фронтальной и профильной плоскостям проекций?

9. Изобразите чертёж произвольной фронтально-проецирующей плоскости, заданной треугольником.

10. Как измерить натуральную величину углов наклона этой плоскости к горизонтальной и профильной плоскостям проекций?

11. Изобразите чертёж произвольной профильно-проецирующей плоскости, заданной двумя параллельными прямыми.

12. Как измерить натуральную величину углов наклона этой плоскости к горизонтальной и фронтальной плоскостям проекций?

13. Какую плоскость называют плоскостью уровня?

14. Сформулируйте эпюрный признак плоскости уровня.

15. Какую плоскость называют горизонтальной? Изобразите чертёж этой плоскости, заданной треугольником.

16. Какую плоскость называют фронтальной? Изобразите чертёж этой плоскости, заданной любой плоской фигурой.

17. Какую плоскость называют профильной? Изобразите чертёж этой плоскости, заданной треугольником.

18. Какую плоскость называют плоскостью общего положения? Как проецируются фигуры, расположенные в этой плоскости?

Вопросы для самопроверки

 

1. В чем состоит условие принадлежности прямой плоскости?

2. В чем состоит условие принадлежности точки плоскости?

3. Какого условия достаточно, чтобы по чертежу можно было бы установить принадлежность точки или прямой проецирующей плоскости?

4. Что такое прямая наибольшего наклона плоскости?

5. Как расположена прямая наибольшего наклона плоскости общего положения к горизонтальной плоскости проекций в пространстве и на чертеже?

6. Как определить на чертеже натуральную величину наибольшего угла наклона плоскости общего положения к горизонтальной плоскости проекций?

7. Как определить на чертеже натуральную величину наибольшего угла наклона плоскости общего положения к фронтальной плоскости проекций?

8. Как построить на чертеже проекции точки пересечения прямой общего положения с проецирующей плоскостью?

9. Как построить на чертеже проекции точки пересечения проецирующей прямой с плоскостью общего положения?

10. Как построить на чертеже проекции линии пересечения проецирующей плоскости с плоскостью общего положения?

11. Изложите последовательность построения на чертеже проекций точки пересечения прямой общего положения с плоскостью общего положения.

12. Как определяется на чертеже видимость проекций прямой и плоскости относительно друг друга?

13. В чем состоит условие перпендикулярности прямой плоскости?

 

1.4. Последовательность выполнения построений
графического решения задачи 1 [ 1 ]

Задача – построить линию пересечения треугольников АВС и ЕДК и показать видимость их в проекциях. Определить натуральную величину треугольника АВС.

 

Многогранные поверхности

 

1.5.1. Образование многогранных поверхностей и построение
их комплексных чертежей

 

Многогранником называется совокупность таких плоских многоугольников, у которых каждая из сторон является одновременно стороной другого многоугольника, но только одного.

Многоугольники эти называются гранями, стороны их – ребрами, а вершины – вершинами многогранника. Совокупность всех граней многогранника называется его поверхностью.

В дальнейшем будем рассматривать только выпуклые многогранники, т. е. такие, которые можно расположить по одну сторону от плоскости любой из его граней.

Образование поверхностей некоторых многогранников подчинено определенным законам. Так, боковая поверхность призм (призматическая поверхность) образуется (рис. 55, а) при таком движении прямой l – образующей по ломаной направляющей m, когда прямая l остается во время движения параллельной своему первоначальному положению.

Боковая поверхность пирамид (пирамидальная поверхность) получается (рис. 55, б) при движении прямолинейной образующей l, проходящей через фиксированную точку S, по направляющей m.

Таким образом, по способу образования поверхности многогранников относятся к линейчатым поверхностям, так как в образовании их участвует прямая линия – образующая.

Построение проекции многогранника на некоторой плоскости сводится обычно к построению проекций точек – вершин многогранника (рис. 56).

Например, проецируя пирамиду SABC на плоскость П¢, строят вначале проекции вершин: S’, A’, B’, C’. Соединив затем проекции точек отрезками прямых, получают проекцию пирамиды.

Таким образом, на комплексном чертеже многогранники изображаются проекциями своих вершин и ребер.

Для большей выразительности проекции вершин многогранника на чертеже рекомендуется отмечать кружками с просветом диаметром
1,5…2 мм, выполненными от руки или с помощью трафарета.

Для облегчения реконструкции многогранника, т. е. построения его положения в пространстве относительно заданной системы плоскостей проекций, следует на чертежах обозначать проекции его вершин прописными буквами латинского алфавита (рис. 57). Это условие особенно необходимо соблюдать в тех случаях, когда некоторые из ребер многогранника являются проецирующими прямыми.

В этом случае при реконструкции многогранника можно получить по комплексному чертежу не одно, а несколько решений.

Например, по комплексному чертежу куба (рис. 57, а), на котором проекции его вершин не обозначены, при реконструкции можно получить четыре различно расположенные в пространстве призмы (рис. 57, б, в, г, д).

Таким образом, если у многогранника имеются ребра профильного или проецирующего положения, а также при совпадении проекций каких-либо вершин или ребер, то обратимость чертежа достигается либо введением буквенных обозначений проекций вершин многогранника (рис. 58), либо построением профильной проекции многогранника (рис. 59).

 

Общие положения

 

Рассматривая в общем случае вопрос о пересечении какого-либо многогранника, например пирамиды SABC (рис. 63), с плоскостью ∑ (сигма) общего положения, нетрудно убедиться в том, что в сечении получается многоугольник. Вершинами его служат точки пересечения рёбер многогранника с секущей плоскостью, а сторонами – отрезки прямых пересечения граней многогранника с секущей плоскостью.

Таким образом, задачу на построение сечения многогранника плоскостью общего положения можно свести либо к многократному решению задачи на пересечение прямой с плоскостью, либо к многократному решению задачи на взаимное пересечение двух плоскостей.

Так как решение первой задачи значительно проще, нежели решение второй, то обычно при построении сечения многогранника плоскостью общего положения вначале строят вершины сечения, как точки пересечения рёбер многогранника с секущей плоскостью, а затем соединяют отрезками прямых каждые две вершины, лежащие в одной и той же грани многогранника. При этом стороны многоугольника сечения, лежащие в видимых проекциях граней многогранника, на чертеже будут видимыми, а лежащие в невидимых гранях – невидимыми.

 

Ι.5.4.Ι. Пересечение многогранника с проецирующей

Плоскостью

При построении сечения многогранника, например пирамиды SABC (рис. 64, а), проецирующей плоскостью ∑, исходят из того, что со следом ∑₂ этой фронтально-проецирующей плоскости совпадает одна из проекций сечения многогранника. Вершины многоугольника сечения представляют собой точки пересечения прямых SA, SB, и SC – рёбер многогранника, с секущей фронтально-проецирующей плоскостью ∑.

На следе ∑₂ секущей плоскости (рис. 64, б) выявляют положения фронтальных 1₂, 2₂, и 3₂ проекций вершин многоугольника сечения.

На основании принадлежности точек 1, 2 и 3 соответственно прямым SA, SB, SC (рис. 64, в) строят их горизонтальные 1₁, 2₁ и 3₁ проекции.

Попарно соединив (рис. 64, г) отрезками прямых горизонтальные проекции вершин, лежащих в одной грани, получают вторую – горизонтальную проекцию сечения пирамиды SABC фронтально-проецирующей плоскостью.

На чертеже (рис. 65) представлен пример построения проекций сечения пирамиды SABC горизонтально-проецирующей плоскостью.

Ι.5.4.2. Пересечение многогранника с прямой.

Общие положения

 

В связи с тем, что любой многогранник представляет собой некоторую совокупность отдельных граней – плоскостей (рис. 66, а), вопрос о пересечении прямой с многогранником может быть сведён к нахождению точек пересечения этой прямой с соответствующими гранями многогранника.

Тогда, по аналогии с определением точки пересечения прямой с плоскостью, задачу на построение точек пересечения прямой с многогранником осуществляют в следующей последовательности:

- заданную прямую (рис. 66, б) заключают во вспомогательную секущую плоскость, чаще всего в проецирующую;

- строят сечение многогранника вспомогательной секущей плоскостью (рис. 66, в);

- определяют точки пересечения прямой с контуром сечения
(рис. 66, г). Рассмотрим примеры построения проекций точек пересечения прямых частного и общего положений с многогранником на конкретных примерах.

 

Ι.5.4.3. Пересечение многогранника с проецирующей прямой

На чертеже (рис. 67, а) заданы пирамида SABC и горизонтально-проецирующая прямая m. Требуется построить проекции точек пересечения прямой с многогранником. Из анализа расположения проекций фигур относительно друг друга и плоскостей проекций следует, что прямая пересекается с гранью SAB боковой поверхности пирамиды. А так как прямая m является горизонтально-проецирующей, то с горизонтальной m₁ проекцией этой прямой совпадает и горизонтальная К₁ проекция точки К пересечения прямой m с гранью SAB пирамиды (рис. 67, б). Для построения фронтальной проекции точки К исходят из принадлежности её плоскости – грани SAB.

На горизонтальной плоскости проекций через К₁ проводят произвольную прямую, принадлежащую грани S₁A₁B₁, например – прямую S₁F₁, и строят её фронтальную S₁F₁ проекцию.

В том месте, где фронтальные проекции прямых m и SF пересекаются, находится фронтальная К₂  проекция точки пересечения горизонтально-проецирующей прямой m с пирамидой SABC.

На рис. 68 представлен пример построения проекций точек пересечения фронтально-проецирующей прямой n с пирамидой SABC.

Из анализа взаимного расположения проекций фигур на чертеже следует, что прямая n пересекается с гранями SAB и SAC пирамиды.

С фронтальной n₂ проекцией прямой совпадают проекции 3₂ и 4₂ точек пересечения её с гранями пирамиды.

На основании принадлежности точек 3 и 4 соответствующим граням строят их горизонтальные проекции.

В точках пересечения горизонтальных проекций прямой n и прямых S₁ и S₂ находятся проекции 3₁ и 4₁ точек пересечения фронтально-проецирующей прямой n с пирамидой SABC.

 

Ι.5.4.4. Пересечение многогранника с прямой общего положения

 

На чертеже (рис. 69, а) представлены проекции пирамиды SABC и прямой m общего положения.

Из анализа взаимного расположения проекций фигур на чертеже следует, что прямая m пересекается с гранями SAB и SBC пирамиды.

Задачу на построение проекций точек пересечения прямой m общего положения с гранями пирамиды решают в следующей последовательности:

1. Заключают прямую общего положения во вспомогательную проецирующую плоскость. На чертеже (рис. 69, б) прямая m заключена в горизонтально-проецирующую плоскость ∑, след которой совпадает с горизонтальной m₁ проекцией прямой m.

2. Строят многоугольник сечения пирамиды плоскостью ∑ (рис. 69, в).

3. Определяют положение проекций точек 4 и 5 пересечения прямой m с контуром фигуры сечения пирамиды вспомогательной секущей плоскостью ∑ (рис. 69, г). Отмеченные точки являются искомыми точками пересечения прямой m общего положения с многогранником – пирамидой SABC.

На чертеже (рис. 70) представлен пример решения той же задачи, но прямая общего положения заключена теперь уже во вспомогательную фронтально-проецирующую плоскость.

 

Ι.5.4.5. Пересечение многогранника с плоскостью общего положения

 

Выше отмечалось, что задачу на построение сечения многогранника (рис. 71), например пирамиды SABC, плоскостью общего положения обычно сводят к многократному решению задачи на пересечение прямой с плоскостью. Для этого вначале строят вершины многоугольника сечения, как точки пересечения рёбер SA, SB и SC многогранника с секущей плоскостью. А затем соединяют отрезками прямых каждые две вершины многоугольника сечения, лежащие в одной и той же грани многогранника.

Рассмотрим решение конкретных задач на построение проекций сечения многогранника плоскостью общего положения.

На чертеже (рис. 72, а) изображены: трёхгранная пирамида АВС и секущая плоскость a (альфа) общего положения, заданная двумя пересекающимися прямыми: фронталью – f  и горизонталью – h.

Анализируя расположение заданных фигур на чертеже (рис. 72, б), устанавливают, что основание пирамиды – треугольник АВС и прямая h расположены в горизонтальной плоскости проекций, так как их фронтальные проекции совпадают с осью X.

Это позволяет определить на чертеже положения точек E и F пересечения прямой h, принадлежащей плоскости a, с гранью АВС многогранника.

Выявив горизонтальные Е₁ и F₁ проекции точек, строят их фронтальные Е₂ и F₂ проекции. Прямая EF (E₁F₁, E₂F₂) представляет собой линию пересечения пирамиды плоскостью общего положения.

Далее предполагают, что с секущей плоскостью a пересекаются рёбра SA, SB и SC боковой поверхности пирамиды.

Проекции прямых SA, SB и SC не параллельны и не перпендикулярны оси проекций X. Это значит, что каждая из прямых занимает в пространстве общее положение.

Тогда для построения проекций вершин сечения боковой поверхности пирамиды необходимо определить положения на чертеже проекций точек пересечения каждой из трёх прямых: SA, SB и SC, – с плоскостью a.

Так как прямые SA, SB и SC и плоскость a занимают общие положения, то для построения проекций точек их взаимного пересечения используют способ вспомогательных секущих плоскостей, в качестве которых чаще всего применяют проецирующие плоскости.

На чертеже (рис. 72, в) прямая SA заключена во вспомогательную фронтально-проецирующую плоскость ∑.

След ∑₂ секущей плоскости совпадает с фронтальной S₂A₂ проекцией прямой SA.

Прямая 1₂2₂ представляет собой фронтальную проекцию линии взаимного пересечения двух плоскостей: заданной – a  и вспомогательной – ∑.

Строят горизонтальную 1₁2₁ проекцию линии пересечения плоскостей и на горизонтальной плоскости проекций рассматривают взаимное расположение проекций прямых SA и 1-2 .

Горизонтальные 1₁2₁ и S₁A₁ проекции прямых пересекаются в точке 4₁. Фронтальная 4₂ проекция точки пересечения располагается на следе ∑₂ вспомогательной секущей плоскости.

Точка 4 (4₁, 4₂) является искомой точкой пересечения прямой SA с плоскостью a, так как она принадлежит обеим фигурам:

- прямой SA, потому что проекции точки 4 расположены на соответствующих проекциях этой прямой,

- плоскости a, потому что проекции точки 4 расположены на соответствующих проекциях 1 2, принадлежащей плоскости a.

Для построения точки пересечения прямой SC с плоскостью a заключает прямую во вспомогательную фронтально-проецирующую плоскость θ (тэта) (рис. 72, г).

След θ₂ секущей плоскости совпадает с фронтальной S₂C₂ проекцией прямой SС. Прямая 1₂2₂ представляет собой фронтальную проекцию линии взаимного пересечения двух плоскостей: заданной – a и вспомогательной – θ.

 Строят горизонтальную 1₁2₁ проекцию линии взаимного пересечения двух плоскостей и на горизонтальной плоскости проекций рассматривают взаимное расположение проекций прямых S C и 1-2. Горизонтальные 1₁2₁ и S₁C₁ проекции прямых пересекаются в точке 5₁. Фронтальная 5₂ проекция точки пересечения располагается на следе θ₂ секущей плоскости.

Точка 5 (5₁, 5₂) является искомой точкой пересечения прямой SС с плоскостью a, так как она принадлежит обеим фигурам:

- прямой SС, потому что проекции точки 5 располагаются на соответствующих проекциях этой прямой;

- плоскости a, потому что проекции точки 5 располагаются на
соответствующих проекциях прямой 1-2, принадлежащей плоскости a.

Для построения точки пересечения прямой SB с плоскостью a
(рис. 72, д) заключают прямую во вспомогательную горизонтально-проецирующую плоскость Ф (фи).

След Ф₁ секущей плоскости совпадает с горизонтальной S₁B₁ проекцией прямой SВ.

Прямая 1₁2₁ представляет собой горизонтальную проекцию линии взаимного пересечения двух плоскостей: заданной a и вспомогательной – Ф.

Строят фронтальную 1₂2₂ проекцию линии взаимного пересечения двух плоскостей и на фронтальной плоскости проекций рассматривают взаимное расположение проекций прямых SB и 1-2. Фронтальные 1₂2₂ и S₂B₂ проекции прямых не пересекаются. Это означает, что в пространстве прямая SB не пересекается с плоскостью a.

Итак, (рис. 72, e) в результате выполненных построений выявлены положения проекций вершин – точки F, 4, 5, E многоугольника, который должен получиться при рассечении пирамиды SABC плоскостью a общего положения.

Попарно соединив отрезками прямых каждые две одноименные проекции точек, лежащих в одной и той же грани многогранника, получают проекции F₁, 4₁, 5₁, E₁, F₁ и F₂, 4₂, 5₂, E₂, F₂ многоугольника сечения пирамиды SABC плоскостью общего положения, заданной двумя пересекающимися прямыми: фронталью – f и горизонталью – h.

Известно, что от расположения фигур в пространстве относительно заданной системы плоскостей проекций – общего или частного – в значительной степени зависит трудоемкость решения той или иной метрической или позиционной задачи.

На чертеже (рис. 73, а) секущая плоскость a (a₁, a₂) и ребра боковой поверхности пирамиды: SА ( S₁A₁, S₂A₂),  SC ( S₁C₁, S₂C₂ ) и SB (S₁B₁, S₂B₂) занимают общие положения относительно заданной системы плоскостей проекций.

Если же секущую плоскость a общего положения преобразовать в проецирующую (рис. 73, б), то трудоёмкость построения проекций точек пересечения ребер пирамиды с плоскостью a, весьма существенно уменьшится. В связи с тем, что секущая плоскость a задана на чертеже двумя пересекающимися прямыми: фронталью – f и горизонталью – h, её легко преобразовать в проецирующую, например, способом замены плоскостей проекций.

Для этого достаточно на чертеже на горизонтальной плоскости проекций провести новую ось проекций П₁/П₄ перпендикулярно горизонтальной h₁ проекции горизонтали h и построить новую проекцию f₄ прямой f, так как горизонтальная прямая h преобразуется в новой П₁/П₄ системе плоскостей проекций в точку h₄ расположенную непосредственно на новой оси проекций. Таким образом, в новой системе плоскостей проекций П₁/П₄ плоскость a общего положения является проецирующей, так как теперь одна из её проекций a₄ представляет собой прямую линию, совпадающую с проекцией f₄ фронтальной прямой. В новой системе плоскостей проекций П₁/П₄ строят проекцию пирамиды: S₄ A₄ B₄ C₄.

Выполненное преобразование позволяет не только сразу выявить положения проекций 4₄ и 5₄ точек пересечения соответственно прямых SА и SC с секущей плоскостью (рис. 73, в), но и установить, что прямая SB в пространстве вовсе не пересекается с плоскостью a, так как прямая S₄ B₄ не пересекается со следом a₄ секущей плоскости. Значит, прямая SВ с плоскостью a не пересекается. А в решении задачи по первому варианту не пересечение прямой SВ с плоскостью a выявилось только с помощью построения линии пересечения плоскости a вспомогательной горизонтально-проецирующей плоскостью Ф, проходящей через прямую SB. На основании принадлежности точек 1, 4, 2 и 5 соответствующим прямым строят их фронтальные проекции: 1₂, 4₂, 5₂ и 2₂. Попарно соединив отрезками прямых одноимённые проекции точек, лежащих в одной и той же грани, получают проекции: 1₁, 4₁, 5₁, 1₁ и 1₂, 4₂, 5₂, 1₂ – многоугольника сечения пирамиды SABC плоскостью a общего положения.

 

Вопросы для самопроверки

 

1. Сформулируйте закономерность образования призматической поверхности.

2. Сформулируйте закономерность образования пирамидальной поверхности.

3. Какая поверхность называется многогранной?

4. Какой многогранник называется выпуклым?

5. Каким образом изображаются многогранники на чертежах?

6. В каких случаях обозначение проекций вершин многогранника является обязательным?

7. Каким образом достигается обратимость чертежа многогранника?

8. Каким образом определяется видимость проекций ребер многогранника? Покажите на примере.

9. Сформулируйте признак принадлежности прямой линии многогранной поверхности.

10. Сформулируйте признак принадлежности точки многогранной поверхности.

11. На чем основано построение проекций точки пересечения проецирующей прямой с многогранной поверхностью?

12. На чем основано построение проекций точки пересечения многогранника с проецирующей плоскостью?

13. Изложите последовательность определения положения проекций точек пересечения прямой общего положения с многогранником.

14. На чем основано применение проецирующих плоскостей для построения проекций точек пересечения прямой общего положения с многогранником?

15. Каким образом и в какой последовательности выполняют построение проекций линии пересечения многогранника с плоскостью общего положения?

 

 

Общие положения

 

В связи с тем, что любая многогранная поверхность (рис. 74) представляет собой некоторую совокупность отдельных граней – плоскостей, ограниченных их сторонами – рёбрами, вопрос о построении линии взаимного пересечения многогранных поверхностей обычно сводят к многократному решению задачи либо на построение линии взаимного пересечения двух плоскостей, либо на пересечение рёбер одного многогранника с гранями другого.

Так как решение второй задачи значительно проще, нежели первой, то обычно при построении линии взаимного пересечения многогранников вначале строят вершины сечения, как точки пересечения рёбер одного из многогранников с гранями другого. А затем соединяют отрезками прямых каждые две вершины, лежащие в грани первого многогранника и одной грани второго многогранника.

Линиями пересечения двух многогранников в общем случае являются пространственные многоугольники. В зависимости от вида многогранников и их взаимного расположения, линиями пересечения могут быть один или несколько пространственных многоугольников. Линиями пересечения двух выпуклых многогранников являются один или два многоугольника.

Если один из многогранников полностью пересекается вторым, то получают две линии пересечения – линию входа одного многогранника в другой и линию выхода. Такое взаимное пересечение геометрических фигур называют полным проницанием. Если же один многогранник частично пересекается, т. е. как бы не полностью врезается в поверхность другого, то получают лишь одну замкнутую линию их взаимного пересечения. Такое взаимное пересечение выпуклых многогранников называют неполным проницанием или врезкой.

Проекции линии пересечения двух многогранников располагаются внутри контуров наложения одноименных проекций многогранников. Причем, если проекция какого-либо ребра одного из многогранников не пересекает контур наложения проекций, то ребро не пересекает контур наложения проекций и не пересекает другой многогранник. Вместе с тем, если проекция ребра одного из многогранников пересекает даже обе проекции контура наложения, то это вовсе не означает, что данное ребро пересекает второй многогранник.

Таким образом, линии взаимного пересечения многогранников – пространственные многоугольники – представляют собой некоторую совокупность отрезков прямых, по которым пересекаются между собой грани многогранников. Вершинами многоугольников являются точки пересечения ребер одного многогранника с гранями другого и ребер второго многогранника с гранями первого. Стороны многоугольников строятся как отрезки прямых, соединяющих только те пары вершин, которые принадлежат одной и той же грани первого многогранника, а также и одной грани второго многогранника.

 

Вопросы для самопроверки

 

1. Каким образом в общем случае решается задача на построение линии взаимного пересечения многогранных поверхностей?

2. Какие геометрические фигуры представляют собой в общем случае линии взаимного пересечения многогранных поверхностей?

3. Какое пересечение многогранных поверхностей называют полным и неполным проницанием?

4. Назовите количество и вид линий взаимного пересечения многогранных поверхностей при полном проницании.

5. Назовите количество и вид линий взаимного пересечения многогранных поверхностей при неполном проницании.

6. Где располагаются на чертеже проекции линий взаимного пересечения двух многогранников?

7. Пересекает ли ребро одного из многогранников поверхность другого, если проекция этого ребра пересекают контуры наложений проекций многогранников?

8. С чего начинают построения проекций линий взаимного пересечения пирамидальной и призматической поверхностей?

9. Каким образом можно сократить трудоемкость графических построений линий взаимного пересечения пирамидальной и призматической поверхностей, занимающих общие положения?

 

1.7. Последовательность выполнения построений графического решения задачи 3 [ 1 ]

 

Задача – построить линию пересечения пирамиды с прямой призмой.

 

Общие положения

 

В инженерной практике проектирования и изготовления различных деталей и металлических конструкций из листового материала довольно часто возникает задача построения развёрток различного рода поверхностей с нанесением на них линий пересечения.

Если поверхность представить не в виде абсолютно жёсткой оболочки, а как гибкую, но не растяжимую плёнку, то оказывается, что некоторые из поверхностей можно путём постепенного деформирования (разгибания) совместить с плоскостью так, что при этом не будет ни складок, ни разрывов.

Поверхности, обладающие этим свойством, называются развёртывающимися, а фигура, полученная от совмещения поверхности с плоскостью – развёрткой.

При этом, если рассматривать поверхность и её развёртку как точечные множества, то между ними устанавливается взаимно однозначное соответствие. Это означает, что каждой точке на поверхности соответствует единственная точка развёртки, каждой линии на поверхности соответствует линия на развёртке.

При этом прямая на поверхности переходит в прямую на развёртке, параллельные прямые также переходят в параллельные. Сохраняются длины линий, расположенных на поверхности, величины углов между линиями и площади фигур, ограниченных замкнутыми линиями.

К числу развёртывающихся поверхностей относятся все многогранные поверхности. Развёрткой многогранной поверхности называется плоская фигура, полученная последовательным совмещением с одной и той же плоскостью всех её граней. Поэтому построение развёртки многогранной поверхности сводится, прежде всего, к определению натурального вида каждой из отдельных её граней.

 

Вопросы для самопроверки

 

1. Какая поверхность называется поверхностью вращения?

2. Какие линии используются в качестве образующей для поверхности вращения?

3. Как называется поверхность вращения, имеющая в качестве образующей прямую линию:

- расположенную параллельно оси вращения;

- пересекающуюся с осью вращения;

- скрещивающуюся с осью вращения?

4. Как образуется сферическая поверхность?

5. Какая поверхность называется тором?

6. Какая поверхность называется глобоидом?

7. Что такое параболоид вращения?

8. Что такое эллипсоид вращения?

9. Как образуется сфероид вращения?

10. Что такое гиперболоид вращения? Какие существуют его разновидности?

11. Что такое параллель поверхности вращения?

12. Сколько параллелей можно провести через точку на поверхности вращения?

13. В каком случае параллель поверхности вращения проецируется в натуральную величину? Что представляет собой в этом случае вторая проекция параллели и как она располагается на чертеже относительно проекции оси вращения?

14. Что такое экватор поверхности вращения? Каким образом определяется видимость проекций точек, расположенных, например, на сферической поверхности, относительно экватора?

15. Что такое меридиан поверхности вращения?

16. Сколько меридианов можно провести через точку, расположенную на поверхности вращения?

17. Что такое главный меридиан поверхности вращения?

18. Что такое главная меридиональная плоскость?

19. Каким образом определяется видимость проекций точек, расположенных, например, на поверхности прямого конуса вращения, относительно главной меридиональной плоскости?

20. Какая поверхность называется прямым цилиндром вращения?

21. Является ли поверхность прямого цилиндра вращения проецирующей? Почему?

22. Какая поверхность называется прямым конусом вращения?

23. Является ли поверхность прямого конуса вращения проецирующей? Почему?

24. Сформулируйте признак принадлежности точек поверхности вращения.

25. Сформулируйте эпюрный признак принадлежности точки поверхности вращения.

26. Если на чертеже проекции точки не располагаются на одноименных проекциях образующей, меридиана или параллели поверхности вращения, то принадлежит ли эта точка поверхности?

27. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого цилиндра вращения?

28. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого конуса вращения?

29. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого глобоида?

30. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на сферической поверхности?

 

 

Общие положения

 

Аналогично тому, как при пересечении многогранника с плоскостью (рис. 125) в сечении получается плоская геометрическая фигура, так и линия пересечения поверхности вращения с плоскостью представляет собой в общем случае плоскую геометрическую фигуру, но теперь уже кривую линию. Ее можно рассматривать как геометрическое место точек пересечения таких линий поверхности вращения, как прямолинейные образующие, меридианы или параллели с секущей плоскостью.

 

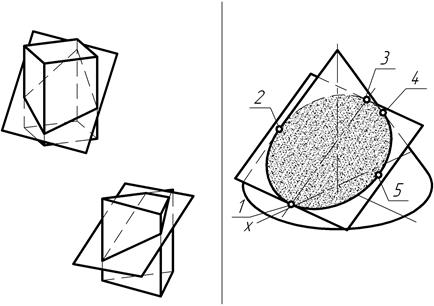
Рис. 125

 

Для построения на чертеже проекций кривой пересечения вначале находят положения отдельных ее точек и затем, соединяя одноименные проекции точек плавными кривыми (обычно по лекалу), получают проекции искомой линии.

Среди точек кривой пересечения, например, прямого конуса вращения с плоскостью общего положения, представленных на рис. 125, имеются такие точки, которые либо выделяются своим особым расположением по отношению к плоскостям проекции и наблюдателю, либо занимают особые места на поверхности вращения. Такие точки кривой пересечения называют опорными. К ним относятся так называемые экстремальные точки и точки видимости. Экстремальными точками являются такие точки линии пересечения, о которых обычно говорят, что они – самые, самые. Самая высшая (например, точка 3) и самая низшая (точка 1), а также самая дальняя (например, точка 2) и самая ближняя (точка 5), самая левая и самая правая точки по отношению к наблюдателю, расположенному лицом к фронтальной плоскости проекций. Точки видимости (например, точки 2 и 4) разграничивают проекции линии пересечения на видимую и невидимую части по отношению к той или иной плоскости проекций. Остальные точки кривой пересечения называются произвольными.

Если все произвольные точки кривой пересечения могут быть найдены одним общим приемом, рассмотренным ниже, то для нахождения положения опорных точек приходится для каждой из них искать свой особый прием построения, зависящий не только от вида самой поверхности вращения, но и от расположения поверхности и секущей плоскости друг относительно друга и плоскостей проекций.

Рассмотрим некоторые особенности построения опорных и произвольных точек кривой сечения на примере пересечения прямого конуса вращения с плоскостью общего положения (рис. 126, а).

 

 

 

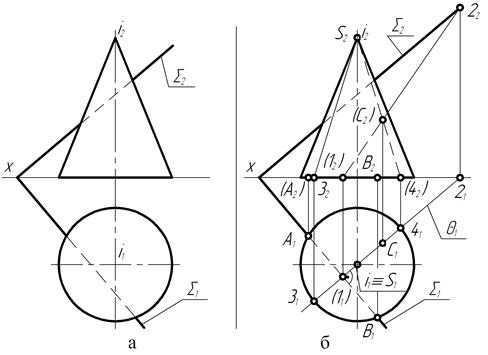
Рис. 126

 

На чертеже секущая плоскость å (сигма) задана следами: фронтальным – å₂ и горизонтальным – å₁. Это – один из способов задания плоскости на чертежах. Вспомним, что следом плоскости называется прямая линия, которая получается при пересечении заданной плоскости с какой-либо плоскостью проекций. И так как на чертеже оба следа плоскости располагаются под некоторым углом к оси проекции Х, то плоскость представляет собой плоскость общего положения. А поэтому кривая пересечения спроецируется на обе плоскости проекции: фронтальную и горизонтальную – в искаженном виде.

Анализ взаимного расположения заданных фигур и их расположения относительно плоскостей проекций позволяет установить на чертеже положения проекций самых низших точек кривой пересечения (рис. 126, б).

Обратите внимание на то, что фронтальная проекция основания конуса располагается непосредственно на оси проекции Х. Это значит, что основание конуса – окружность – не только лежит в горизонтальной плоскости проекции, но и пересекается со следом Σ₁ секущей плоскости в точках А₁ и В₁. Фронтальные А₂ и В₂ проекции точек располагаются на оси проекций Х. На этом основании можно сделать вывод о том, что точки
А (А₁, А₂) и В (В₁, В₂) являются самыми низшими точками кривой пересечения.

Вместе с тем, рассматривая расположение горизонтальных проекций точек А и В на чертеже, устанавливаем, что точка В является, кроме того, самой близкой к наблюдателю точкой, располагающейся на видимой части поверхности конуса. Поэтому ее фронтальная проекция будет видимой, а проекция точки А₂ – невидимой. Таким образом, одна и та же точка кривой пересечения в некоторых случаях может быть, с одной стороны, самой низшей, а с другой – самой близкой.

Естественно предположить, что если кривая пересечения имеет самые низшие точки, то должна же быть и самая высокая точка. Как определит ее положение на чертеже? Опять-таки на основании анализа расположения на чертеже проекций заданных геометрических фигур.

Секущая плоскость Σ (сигма) является плоскостью общего положения. Она определенным образом наклонена к горизонтальной плоскости проекций и по отношению к наблюдателю является восходящей. Поэтому самая высшая точка кривой пересечения фигур, как принадлежащая секущей плоскости, должна находиться, с одной стороны, на линии наибольшего наклона плоскости Σ к горизонтальной плоскости проекции. А эта линия заданной секущей плоскости располагается перпендикулярно горизонтальному Σ₁ ее следу. С другой стороны, самая высшая точка кривой пересечения принадлежит и конической поверхности, и поэтому должна располагаться на одном из меридианов. А что такое меридиан? Это есть сечение поверхности вращения плоскостью, проходящей через ось вращения.

При заданном на чертеже расположении оси вращения конуса эта плоскость является горизонтально-проецирующей. Значит, след меридиональной плоскости, в которой находится самая высшая точка кривой пересечения фигур, должен расположиться на чертеже обязательно перпендикулярно горизонтальному Σ₁ следу секущей плоскости.

 

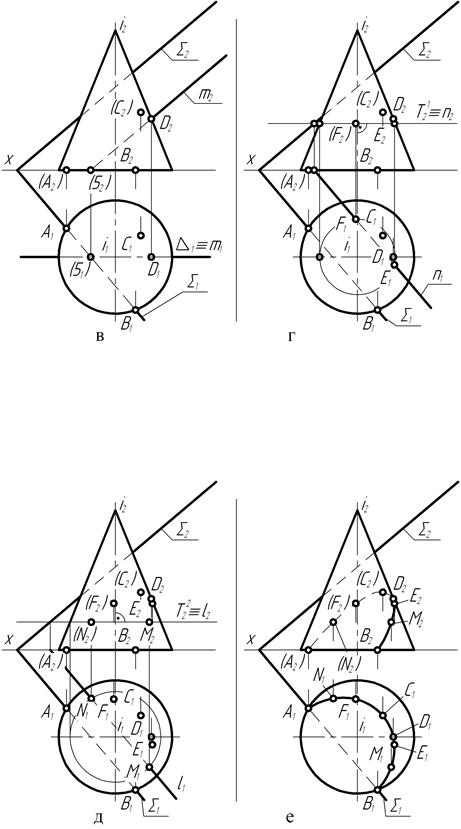
Рис. 126

 

Для определения конкретного положения на чертеже проекций точки видимости кривой пересечения воспользуемся вспомогательной секущей плоскостью, которая по сути дела является как бы продолжением главной меридиональной плоскости конуса. На чертеже эта вспомогательная секущая плоскость обозначена своим горизонтальным λ₁ (лямбда – 1) следом.

В пересечении вспомогательной фронтальной плоскости λ с плоскостью Σ образуется фронтальная прямая m с проекциями m₁ и m₂. Линия пересечения плоскости λ (лямбда) с конусом есть не что иное, как его главный меридиан, фронтальной проекцией которого является треугольник, с одной из сторон которого в точке Д₂ пересекается прямая m₂. Горизонтальная Д₁ проекция располагается на следе λ₁.

Точка Д (Д₁, Д₂) принадлежит секущей плоскости Σ и прямому конусу вращения. И так как проекция точки Д располагается на соответствующих проекциях главного меридиана поверхности вращения, она является следующей искомой точкой кривой пересечения, а именно – точкой видимости.

Таким образом, посредством выполнения определенных приемов, обусловленных изображением геометрических фигур на чертеже, удалось выявить положения проекций основных опорных точек кривой пересечения.

Для определения положения на чертеже проекций произвольных точек кривой пересечения используют известный способ вспомогательных секущих плоскостей.

Сущность его, применительно к рассматриваемому примеру – пересечению конической поверхности с плоскостью общего положения, состоит в том, что заданная плоскость и поверхность вращения пересекаются одной вспомогательной секущей плоскостью, чаще всего проецирующей или плоскостью уровня. Однако в некоторых случаях в качестве секущей плоскости может быть использована и плоскость общего положения.

Выбор вида и положения на чертеже вспомогательной секущей плоскости определяется условием: в пересечении поверхностей вращения с этой плоскостью должны получаться простые геометрические линии – прямые или окружности. Это условие относится непосредственно только к поверхностям вращения, так как плоскости пересекаются друг с другом в любом случае по прямой. Важно при этом, чтобы окружности сечения – параллели – проецировались бы на одну из плоскостей проекций в натуральную величину.

Для рассматриваемого примера (рис. 126, г) указанным выше условиям отвечает горизонтальная секущая плоскость, заданная на чертеже своим фронтальным T₂¹ (тау) следом, расположенным параллельно оси проекции Х.

Именно в сечении прямого конуса вращения этой плоскостью образуется плоская геометрическая линия – окружность, представляющая собой параллель конической поверхности, так как ось вращения конуса перпендикулярна горизонтальной плоскости проекций.

Можно было бы использовать в качестве вспомогательной секущей плоскости либо горизонтально-проецирующую плоскость, проходящую через ось вращения конуса, то есть конкурирующую с меридиональной плоскостью конической поверхности, либо плоскость общего положения, проходящую через вершину конуса. В сечении конуса каждой из указанных плоскостей также образуются простые геометрические фигуры – треугольники. Однако применение таких вспомогательных секущих плоскостей несколько увеличивает трудоемкость выполнения графических построений.

При пересечении вспомогательной секущей плоскости Т (τ - тау) с плоскостью Σ (сигма) образуется прямая частного положения, а именно – горизонтальная прямая. Это обстоятельство также имеет весьма существенное значение для уменьшения трудоемкости графических построений, так как проекции прямых уровня в плоскостях общего положения, заданных на чертеже следами, очень легко строить – горизонтальная проекция горизонтальной прямой плоскости Σ, например, должна располагаться параллельно ее горизонтальному Σ₁ следу.

На фронтальной плоскости проекций между точкой С₂ – самой высшей точкой и точками А₂ и В₂ – самыми низшими проекциями точек кривой пересечения проводят след – Τ₂¹ первой вспомогательной горизонтальной секущей плоскости. И строят горизонтальные проекции линий сечения фигур плоскостью Т (тау), представляющие собой: окружность – горизонтальную проекцию параллели конической поверхности и прямую n₁ – проекцию горизонтальной прямой n плоскости.

Рассматривают их взаимное расположение и устанавливают, что горизонтальная проекция параллели конуса – окружность и прямая n₁ пересекаются в точках Е₁ и F₁. Фронтальные проекции этих точек: Е₂ и F₂  находят на следе Τ₂¹  секущей плоскости.

На основании того, что проекции точек F (F₁, F₂) и Е (Е₁, Е₂) располагаются на соответствующих проекциях прямой n (n₁, n₂), принадлежащей плоскости Σ, и проекциях параллели конуса, делают вывод о том, что точки E и F принадлежат одновременно плоскости Σ, и поверхности конуса вращения. А это значит, что точки E и F принадлежат кривой пересечения прямого конуса вращения с плоскостью общего положения.

Подобным образом (рис. 126, д) определяют положения на чертеже ещё двух произвольных точек N (N₁, N₂ ) и М (М₁, М₂) кривой пересечения с помощью всё той же вспомогательной горизонтальной секущей плоскости Т (тау), но теперь уже проведённой несколько ниже фронтальных проекций точек F₂ и Е₂.

С помощью способа вспомогательной секущей плоскости можно определить положения на чертеже проекций некоторого множества произвольных точек кривой пересечения. Соединив затем плавной кривой линией по лекалу одноимённые проекции точек с учётом видимости их на чертеже, получают (рис. 126, е) фронтальную и горизонтальную проекции кривой пересечения прямого конуса вращения с плоскостью Σ общего положения.

На рис. 127 представлено наглядное изображение – прямоугольная изометрия заданных на чертеже фигур: прямого конуса вращения и секущей плоскости общего положения, а также кривая линия, полученная в результате их взаимного пересечения. На кривой обозначены положения её опорных и произвольных точек.

Таким образом, рассмотренный пример построения на чертеже проекций кривой пересечения поверхности вращения с плоскостью общего положения свидетельствует о значительной трудоемкости выполненных при этом графических построений.

 

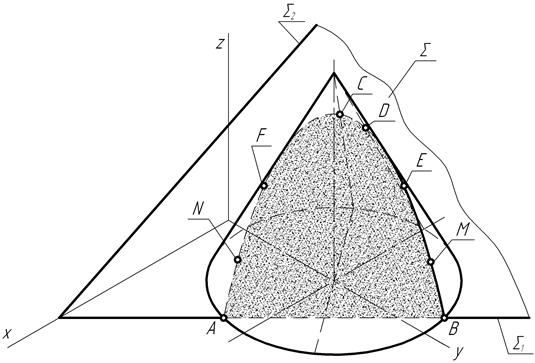
Рис. 127

 

Вместе с тем трудоёмкость решения подобной задачи удаётся значительно сократить преобразованием секущей плоскости общего положения в проецирующую или плоскость уровня. Это объясняется тем, что в случае использования в качестве секущей плоскости проецирующей или плоскости уровня, на чертеже всегда имеется одна из проекций кривой пересечения этой плоскости с поверхностью вращения. Тогда использование способа вспомогательных секущих плоскостей для определения положения проекций произвольных точек кривой пересечения вовсе отпадает, так как построение второй проекции кривой пересечения по сути дела сводится лишь к построению недостающих проекций её точек. Выполнение же этих построений на основании эпюрного признака принадлежности точки поверхности вращения не вызывает особых затруднений. Значительно упрощается при этом и решение такой сложной задачи, как определение положения на чертеже опорных точек кривой пересечения: экстремальных и точек видимости.

Рассмотрим конкретные примеры построения проекций линий пересечения поверхностей вращения с секущими плоскостями частного положения: проецирующими или плоскостями уровня.

Вопросы для самопроверки

 

1. Какая линия получается в общем случае или пересечении поверхности вращения плоскостью?

2. С каких точек начинают построение кривой пересечения?

3. Какие точки кривой пересечения называются опорными? 

4. Что такое точки видимости?

5. Какой способ в общем случае используется для определения положений на чертеже произвольных точек кривой пересечения? В чем состоит его сущность?

6. Каким условием определяется выбор вида и положения на чертеже

вспомогательной секущей плоскости для построения проекций произвольных точек кривой пересечения? 

7. Каким образом можно значительно сократить трудоёмкость графических построений проекций кривой пересечения поверхностей вращения с плоскостью общего положения?

8. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, перпендикулярной оси вращения?

9. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, параллельной оси вращения?

10. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, не параллельной и на перпендикулярной оси вращения?

11. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, перпендикулярной оси вращения?

12. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, параллельной оси вращения?

13. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, параллельной образующей?

14. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, не перпендикулярной оси вращения и не параллельной образующей?

15. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, проходящей через вершину?

16. Какой вид имеет сечение сферы плоскостью?

17. Какие графические линии относятся к числу простых?

18. Назовите положения секущей плоскости, при которых прямой цилиндр вращения пересекается по простым графическим линиям?

19. Назовите положения секущей плоскости, при которых прямой конус вращения пересекается по простым графическим линиям?  

20. При каком положении секущей плоскости сферическая поверхность пересекается по окружности?

 

Общие положения

 

Аналогично тому, как в случае пересечения прямой с многогранной поверхностью образуются точки, принадлежащие обеим фигурам: прямой и многограннику, так и при пересечении поверхностей вращения с прямой (рис. 140) образуются точки, принадлежащие и прямой, и поверхности вращения.

В связи с этим для построения проекций точек пересечения прямой с поверхностью вращения представляется возможным использовать в общем случае способ вспомогательной секущей плоскости. Тогда графические построения проекций точек пересечения прямой с поверхностью вращения осуществляются в следующей последовательности:

- прямую заключают во вспомогательную секущую плоскость;

- строят проекции линии пересечения вспомогательной секущей плоскости с поверхностью вращения;

- рассматривают взаимное расположение проекций прямой и линии пересечения поверхности вращения вспомогательной секущей плоскостью;

- точки взаимного пересечения одноимённых проекций прямой и фигуры сечения представляют собой проекции искомых точек пересечения поверхности вращения с прямой;

- на основании эпюрного признака принадлежности точки прямой или поверхности вращения строят вторые проекции искомых точек.

В качестве вспомогательной секущей плоскости используются чаще всего плоскости частного положения – проецирующие или плоскости уровня. Однако в некоторых случаях успешно применяются и плоскости общего положения.

Выбор вида и положения вспомогательной секущей плоскости определяется условием – поверхность вращения должна пересекаться плоскостью по графически простым линиям: прямым или окружности.

Если при пересечении многогранника плоскостью (рис. 141) в любом случае в сечении образуются графически простые фигуры – многоугольники, то сечение поверхности вращения плоскостью представляет собой графически простые фигуры – треугольники, параллелограммы, окружности, лишь при некоторых особых положениях секущей плоскости.

Так, в сечении прямого цилиндра вращения образуются графически простые фигуры – прямоугольник или окружность, только в случае пересечения его плоскостью, параллельной или перпендикулярной оси вращения.

В сечении прямого конуса вращения (рис. 142) образуются графически простые фигуры – треугольник или окружность, только в случае пере-

 

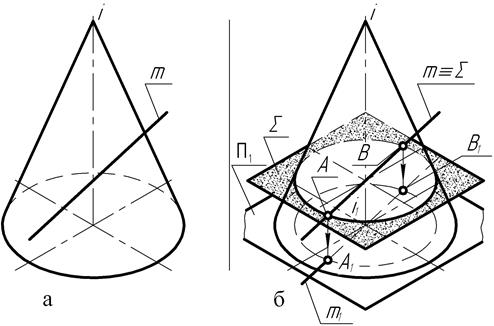
Рис. 140

 

 

 

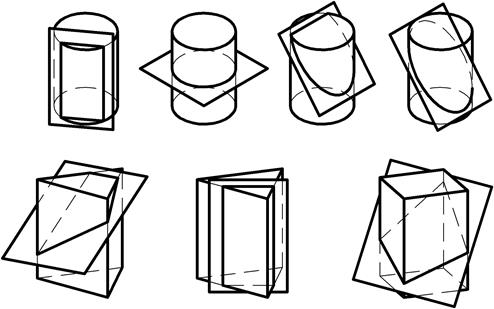
Рис. 140

 

сечения его плоскостью, проходящей через вершину или расположенной перпендикулярно оси вращения.

В тех случаях, когда в сечении поверхности вращения плоскостью невозможно получить графически простые фигуры сечения, приходится строить проекции кривой пересечения – эллипса, параболы, гиперболы и других, а затем определять положения точек пересечения проекций прямой с кривой линией сечения.

В некоторых случаях применение способов преобразования проекционных чертежей, в частности, способа замены плоскостей проекций, позволяют вообще отказаться от использования способа вспомогательной секущей плоскости для определения положения на чертеже проекций точек пересечения прямой с поверхностью вращения.

Рассмотрим особенности построения проекций точек пересечения поверхности вращения с прямой, занимающей в пространстве различные положения, на конкретных примерах.

 

Вопросы для самопроверки

 

1. Изложите последовательность выполнения графических построений проекций точек пересечения прямой с поверхностью вращения в случае применения способа вспомогательной секущей плоскости.

2. Каким условием определяются выбор и расположение на чертеже вспомогательной секущей плоскости?

3. При каком положении секущей плоскости в сечении прямого цилиндра вращения образуются графически простые фигуры?

4. При каком положении секущей плоскости в сечении прямого конуса вращения образуются графически простые фигуры?

5. При каком положении секущей плоскости кривая пересечения сферы проецируется в натуральную величину?

6. На чём основано построение проекций точек пересечения проецирующей прямой с поверхностью вращения?

7. Изложите эпюрный признак принадлежности точки, прямой поверхности вращения.

 

2.6. Последовательность выполнения построений графического решения задачи 6 [ 1 ]

 

Задача – на трёхпроекционном чертеже построить недостающие проекции сквозного четырёхугольного отверстия в сфере заданного радиуса.

 

Графическое решение задачи начинают с того, что на листе чертежной бумаги (ватмане) формата A3 (297´420 мм) карандашом тонкими линиями выполняют рамки формата и чертежа. В правом нижнем углу длинной стороны формата располагают рамку основной надписи.

В центре поля чертежа (рис. 151) размечают и проводят две взаимно перпендикулярные прямые линии: горизонтальную и вертикальную, пересекающиеся в точке О – начале отсчета координат. Пересекающиеся прямые линии являются осями проекции Х, Y и Z .

По числовым значениям координат центра 0 сферы, взятым из таблицы 5 методических указаний [1] в зависимости от номера варианта задачи, строят его проекции. Получают трехпроекционный чертеж сферы заданного радиуса.

По числовым значениям координат строят фронтальные А₂, В₂, С₂ и Д₂ проекции вершин четырехугольника. Попарно соединив отрезками прямых проекции точек, получают на чертеже фронтальную проекцию сквозного отверстия в сфере – многоугольник, представляющий собой вырожденную проекцию линии сквозного отверстия. Такая вырожденная проекция отверстия в сфере получается только в случае пересечения ее четырьмя фронтально-проецирующими плоскостями (отсеками). В пересечении смежных отсеков проецирующих плоскостей образуются ребра А¹-А², В¹-В², С¹-С² и Д¹-Д²  четырехгранника.

 

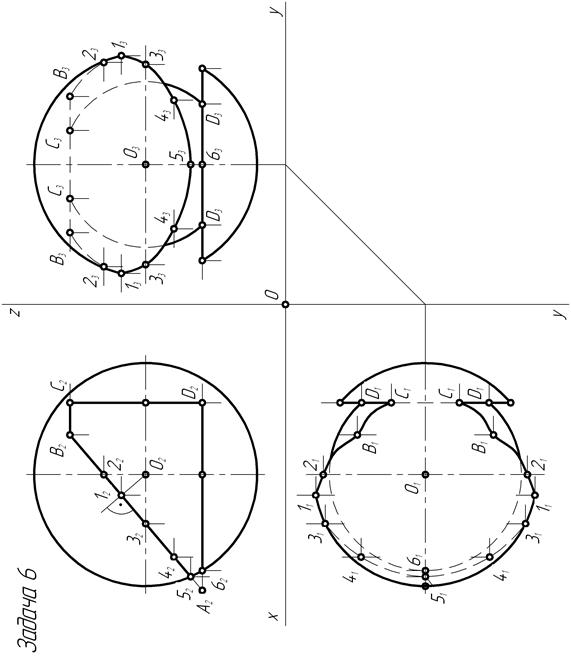
Рис. 151

 

 

Известно, что сфера пересекается плоскостью по окружности. Поэтому линии пересечения сферы с четырехгранником представляют собой отсеки окружностей, соединенные между собой точками пересечения ребер со сферой. В зависимости от расположения секущей плоскости относительно плоскостей проекций окружность сечения проецируется в натуральную величину или в искаженном виде – в виде эллипса.

Таким образом, для построения недостающих проекций линий сквозного четырехугольного отверстия в сфере необходимо построить проекции точек пересечения каждого из ребер четырёхгранника со сферой и проекцией отсеков окружностей пересечения сферы с каждой из четырех граней.

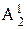
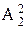
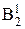
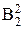
Грань А¹А²В¹В² представляет собой отсек фронтально-проецирующей плоскости. Она располагается наклонно к горизонтальной и профильной плоскостям проекций. Окружность сечения сферы этой плоскостью проецируется на них в виде эллипса. Построение проекций эллипса производят по точкам, взятым на фронтальной проекции отсека окружности сечения сферы, совпадающей с фронтальной  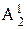проекцией грани. Из множества точек окружности выделяют на чертеже положения фронтальных проекций характерных (опорных) точек, ограничивающих большую (точка 5) и малую (точки 1₁ и 1₂) оси эллипса, расположенных на экваторе (точки 3₁ и 3₂, являющиеся точками видимости для горизонтальной плоскости проекций; точки 2₁ и 2₂, являющиеся точками видимости для профильной плоскости проекций) и главных меридианах, а также несколько произвольных точек.

Построение горизонтальных и профильных проекций точек, выделенных на фронтальной плоскости проекций, производят на основании принадлежности последних сферической поверхности. При этом исходят из того, что проекции точки, принадлежащей сферической поверхности, должны располагаться на соответствующих проекциях её параллели или меридиана.

Грани В¹В²С¹С²В¹ и Д¹Д²А¹А²Д¹ являются отсеками горизонтальных плоскостей уровня. Отсеки их фигур сечения – окружности, проецируются на горизонтальную плоскость проекций в натуральную величину с радиусами, равными радиусам параллелей, плоскости которых совпадают с горизонтальными плоскостями уровня. При этом одновременно определяются положения горизонтальных проекций точек пересечения рёбер В¹-В², С¹-С², Д¹-Д² со сферой. По имеющимся фронтальным и горизонтальным проекциям ребер и отсеков линий сечений строят их профильные проекции.

Грань С¹С²Д¹Д²С¹ является отсеком профильной плоскости уровня. Отсек окружности, расположенный в этой грани, проецируется на профильную плоскость проекций в натуральную величину. Радиус отсека окружности сечения равен радиусу параллели, плоскость которой совпадает с профильной плоскостью уровня грани.

Окончательную обводку линий сквозного отверстия в сфере выполняют с учётом видимости их проекций на чертеже. Видимость проекций точек и линий сферы определяется расположением последних относительно экватора или главных меридианов. Видимые проекции линий выполняют сплошной толстой линией, а невидимые – штриховой.

Общие положения

 

Основу способа вспомогательных секущих сфер (рис. 162) составляют особенности взаимного пересечения так называемых «соосных поверхностей вращения». К ним относятся поверхности, оси вращения которых совпадают, т. е. несколько поверхностей имеют одну общую ось вращения.

Нетрудно видеть, что две соосные поверхности вращения пересекаются друг с другом по окружностям. Причем количество последних равно числу точек пересечения меридианов поверхностей вращения.

Действительно, если одна поверхность образуется вращением меридиана l (l₂), а другая – меридиана D (D₂), представляющего в данном случае окружность, вокруг общей оси i (i₂), то точки А, В, С и К будут описывать окружности, общие для обеих поверхностей.

 

 

Рис. 162

 

При этом, если общая ось поверхностей вращения перпендикулярна какой-либо плоскости проекций, то эти окружности проецируются на одну из них в виде отрезков прямых, соединяющих точки пересечения меридианов и перпендикулярных оси вращения, а на другую – без искажения, в натуральную величину.

Эти особенности взаимного пересечения двух соосных поверхностей вращения, одна из которых является сферой, и составляют основу способа вспомогательных секущих сфер.

Сущность применения способа вспомогательных секущих сфер для построения линии взаимного пересечения двух произвольных поверхностей вращения состоит в том, что каждая из поверхностей вращения пересекается одной и той же вспомогательной сферой. При пересечении вспомогательной сферы с каждой из поверхностей вращения образуются окружности. Точки пересечения полученных окружностей являются общими для каждой из поверхностей вращения и поэтому принадлежат линии взаимного пересечения произвольных поверхностей вращения. При этом пересекающиеся поверхности вращения должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций. Каждая из поверхностей должна содержать семейство окружностей, по которым ее могут пересекать вспомогательные сферы, общие для обеих поверхностей.

В зависимости от расположения осей пересекающихся поверхностей вращения относительно друг друга применяются две разновидности способа вспомогательных секущих сфер.

При взаимном пересечении осей поверхностей вращения применяется способ концентрических секущих сфер, т. е. сфер, проведенных из одного общего центра. Центром проведения таких сфер является точка пересечения осей вращения поверхностей.

Если же оси поверхностей вращения параллельны друг другу или являются скрещивающимися, применяется способ эксцентрических сфер. В этом случае вспомогательные секущие сферы проводятся из разных центров. Рассмотрим особенности применения разновидностей способа вспомогательных секущих сфер для построения линии взаимного пересечения поверхностей вращения.

 

Вопросы для самопроверки

 

1. Что представляет собой в общем случае линия взаимного пересечения поверхностей вращения?

2. В каком случае линия взаимного пересечения поверхностей вращения может представлять собой две плоские кривые линии?

3. Какие поверхности вращения называются поверхностями двойного соприкосновения?

4. Каким образом можно установить принадлежность пересекающихся поверхностей вращения к поверхностям двойного соприкосновения?

5. Что представляют собой линии пересечения поверхностей вращения двойного соприкосновения и через какую прямую они должны проходить?

6. Какие точки кривой пересечения поверхностей вращения называются опорными?

7. Какие точки кривой пересечения поверхностей вращения называются произвольными?

8. Назовите способы построения проекций произвольных точек кривой пересечения поверхностей вращения.

9. В каком случае применяется способ вспомогательных секущих плоскостей?

10. Изложите последовательность выполнения графических построений в случае применения способа вспомогательных секущих плоскостей.

11. Каким условием определяется выбор вида и расположения вспомогательной секущей плоскости?

12. Чем объясняется сокращение трудоёмкости графических построений проекций кривых пересечения двух поверхностей вращения, одна из которых является цилиндрической?

13. В каком случае применяется способ вспомогательных секущих сфер? Перечислите условия, ограничивающие применение этого способа.

14. Какие поверхности вращения называются соосными?

15. Какой вид имеет линия пересечения соосных поверхностей вращения? Чем определяется количество линий пересечения соосных поверхностей вращения?

16. В каком случае сфера является соосной с поверхностью вращения?

17. В чем состоит сущность способа вспомогательных секущих сфер?

18. Какие существуют разновидности способа секущих сфер?

19. Какие сферы называются концентрическими?

20. Какие сферы называются эксцентрическими?

21. На чем основано применение способа концентрических секущих сфер?

22. Какие существуют ограничения в применении способа концентрических секущих сфер?

23. Каким образом определяются значениями минимального и максимального радиусов концентрических секущих сфер?

24. На чем основано применение способа эксцентрических секущих сфер?

25. Какие существуют ограничения в применении способа эксцентрических секущих сфер?

26. На основании какого свойства поверхностей вращения определяются положения центров эксцентрических секущих сфер?

 

3.5. Последовательность выполнения построений графического решения задачи 8 [ 1 ]

 

Задача – построить линию пересечения конуса вращения с
цилиндром вращения.

Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата А3 (297´420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу длинной стороны формата рамку основной надписи. Левую половину поля чертежа (рис. 181, а) используют для построения исходного чертежа задачи. С этой целью на расстоянии 130 мм от верхней рамки поля чертежа проводят горизонтальную прямую линию и на ней на расстоянии 150 мм от левой рамки поля чертежа отмечают положение точки 0 – начала отсчета координат. Через точку 0 проводят вертикальную прямую линию, перпендикулярную горизонтальной прямой. Вводят обозначения осей проекций X, Y и Z. Из табл. 7 методических указаний [1] выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности конуса вращения и цилиндра вращения. 

Определяют положение на чертеже проекций центра (точка К) окружности радиуса R основания конуса вращения. На фронтальной плоскости проекций отмечают положение проекции вершины конуса. С помощью циркуля и линейки тонкими линиями вычерчивают фронтальную и горизонтальную проекции прямого конуса вращения. Ось вращения конуса представляет собой горизонтально-проецирующую прямую. Фронтальную проекцию оси вращения конуса выполняют штрихпунктирной линией.

Затем строят проекции оси вращения цилиндра. Осью вращения цилиндра является фронтально-проецирующая прямая точки Е. Основаниями цилиндра являются окружности радиуса R₁. Образующие цилиндра имеют длину, равную 3R₁, и делятся пополам фронтальной меридиональной плоскостью конуса вращения. Окружности основания и образующие цилиндра выполняют сплошными тонкими линиями. Не следует наносить координатные размеры на исходный чертеж задачи.

Графическому решению задачи должен предшествовать анализ расположения заданных геометрических фигур относительно друг друга и плоскостей проекций.

По условию задачи оси поверхностей вращения – взаимно перпендикулярные скрещивающиеся проецирующие прямые. Ось вращения цилиндра является фронтально-проецирующей прямой. Поэтому цилиндрическая поверхность является проецирующей по отношению к фронтальной плоскости проекций.

 

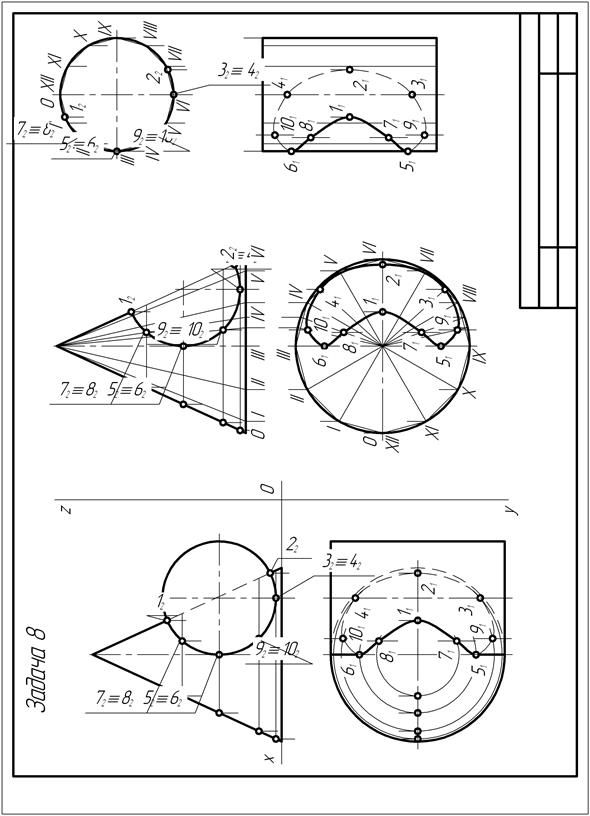
Рис. 181

 

Расположение на чертеже фронтальной проекции цилиндра внутри контура проекции конуса вращения свидетельствует о том, что заданные поверхности пересекаются друг с другом. Линия их взаимного пересечения представляет собой сложную пространственную кривую, точки которой принадлежат обеим поверхностям. Причем точки кривой взаимного пересечения фигур располагаются только на их наружных поверхностях. И так как цилиндрическая поверхность является фронтально-проецирующей, становится вполне очевидным тот факт, что с фронтальной проекцией цилиндра – окружностью, расположенной внутри контура треугольника – проекции главного меридиана прямого конуса вращения, совпадает фронтальная проекция кривой взаимного пересечения заданных поверхностей.

Для построения горизонтальной проекции кривой пересечения конуса с цилиндром на её фронтальной проекции выделяют положения проекций опорных и нескольких произвольных точек.

На фронтальной плоскости проекций отмечают, прежде всего, положения точек 1₂ и 2₂ пересечения фронтальной проекции цилиндра с главным меридианом конуса. Эти точки относятся к числу опорных. Из них: точка 1₂ является фронтальной проекций самой высокой, а точка 2₂ – самой правой точек кривой пересечения фигур. Точки 3₂ и 4₂ являются проекциями самых низших точек кривой пересечения. Точки 5₂ и 6₂ являются проекциями точек видимости горизонтальной проекции кривой пересечения. Точки 7₂, 8₂, 9₂ и 10₂ являются проекциями произвольных точек кривой. Их положение на чертеже выбирается произвольно.

Дальнейшее графическое решение задачи сводится к построению горизонтальных проекций отмеченных точек кривой пересечения заданных геометрических фигур.

Так как цилиндрическая поверхность является фронтально-проецирующей, то построение горизонтальных проекций точек кривой пересечения возможно лишь на основании принадлежности их боковой поверхности конуса. Поэтому построение горизонтальных проекций отмеченных точек кривой выполняют с помощью параллелей прямого конуса вращения.

Для этого на фронтальной плоскости проекций внутри контура треугольника – главного меридиана прямого конуса вращения, через соответствующие фронтальные проекции точек кривой проводят прямые, перпендикулярные фронтальной проекции оси вращения конуса. Отмечают точки пересечения этих прямых с одной из сторон главного меридиана конуса.

Через эти точки проводят линии связи до пересечения с горизонтальным следом главной меридиональной плоскости конуса. Раствором циркуля, равным расстоянию от этих точек до горизонтальной проекции оси вращения конуса, проводят окружности – горизонтальные проекции параллелей соответствующих точек кривой пересечения. И, наконец, через фронтальную проекцию выбранной точки кривой пересечения проводят линию связи и отмечают точки пересечения её с горизонтальной проекцией точек кривой взаимного пересечения поверхностей.

Соединив с помощью лекала плавной кривой горизонтальные проекции точек, получат горизонтальную проекцию кривой пересечения прямого конуса с цилиндром вращения. При этом видимые проекции точек кривой пересечения соединяют сплошной толстой линией, а невидимые – штриховой линией. После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку линий чертежа карандашом. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.

Все цифровые и буквенные обозначения следует выполнить чертежным шрифтом.

 

3.6. Последовательность выполнения построений графического решения задачи 9 [ 1 ]

 

Задача – построить развертки пересекающихся цилиндра вращения  и конуса вращения; показать на развертках линии их пересечения.

 

Построение разверток пересекающихся поверхностей вращения производят в следующей последовательности:

- в заданный конус вписывают 12-гранную пирамиду, в цилиндр 12-гранную призму;

- строят развертки 12-гранной пирамиды и призмы;

- наносят на развертки точки кривой взаимного пересечения поверхностей и соединяют их с помощью лекала плавными линиями.

Для этого в правой части поля чертежа решения задачи 8 (рис. 181, б, в) вычерчивают проекции каждой из заданных поверхностей с кривой пересечения. В прямой конус вращения вписывают 12-гранную пирамиду, а в цилиндр вращения – 12-гранную призму. Отмечают на чертежах положение ребер оснований и боковых поверхностей многогранников. При этом некоторые из ранее рассмотренных точек кривой пересечения оказываются расположенными непосредственно на ребрах боковых поверхностей многогранников. Через другие точки кривой проводят прямые в соответствующих гранях многогранников.

Для построения развертки конуса вращения определяют натуральные величины ребер основания и боковой поверхности пирамиды, а также натуральные величины расстояний от точек кривой пересечения до вершины пирамиды – конуса вращения.

 

 

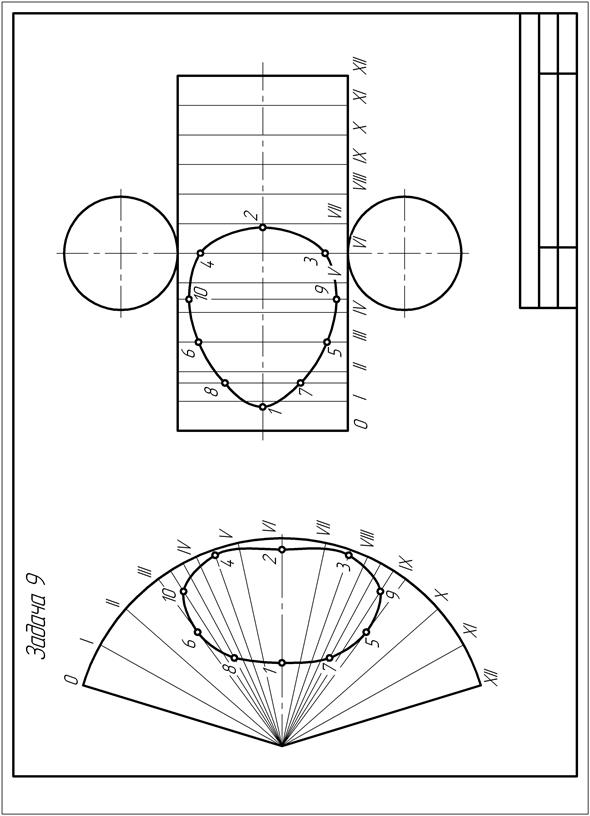
Рис. 182

 

Основание вписанной 12-гранной пирамиды спроецировалось на горизонтальную плоскость проекций в натуральную величину. Для определения натуральной величины расстояния от точек кривой пересечения до вершины пирамиды используют способ вращения вокруг горизонтально-проецирующей прямой, совпадающей с осью вращения конуса. Ребра и прямые боковой поверхности пирамиды, на которых расположены точки кривой пересечения, поворачивают в положение, параллельное фронтальной плоскости проекций. Графически это преобразование выполняют следующим образом: на фронтальной плоскости проекций через фронтальные проекции точек кривой пересечения проводят прямые линии параллельно оси проекций Х до пересечения с главным меридианом конуса. Расстояние проекции точки на главном меридиане до вершины конуса соответствует натуральной величине расстояния точки кривой пересечения до вершины пирамиды.

В левой части поля чертежа (рис. 182, а) произвольно выбирают положение вершины конуса – пирамиды и раствором циркуля, равным натуральной величине образующей конуса, проводят дугу окружности. На ней откладывают 12 равных отрезков, соответствующих натуральной величине ребра основания пирамиды. Соединив их с центром дуги окружности – вершиной пирамиды, конуса, получают развёртку боковой поверхности 12-гранной пирамиды. На ребрах или прямых боковой поверхности пирамиды откладывают натуральные величины расстояний соответствующих точек кривой пересечения до вершины пирамиды, взятые на фронтальной плоскости проекций, на стороне главного меридиана конуса.

Соединив с помощью лекала в определенной последовательности точки плавной линией, получают на развертке боковой поверхности прямого конуса вращения линию его пересечения с цилиндром вращения.

Последовательность построения развёртки цилиндра вращения
(рис. 182, б) аналогична построениям графического решения задачи 4.

При этом натуральные величины ребер основания призмы, а также натуральные величины расстояний точек кривой пересечения от соответствующего ребра боковой поверхности призмы (рис. 182, в), измеряют на фронтальной плоскости проекций. Натуральные величины расстояний точек кривой пересечения от какого-либо основания призмы измеряют на горизонтальной плоскости проекций.

Соединив в определенной последовательности лекальной линией точки, получают на развертке боковой поверхности кривую пересечения цилиндра вращения с прямым конусом вращения.

После построения на развертках кривых пересечения производят окончательную обводку карандашом линий чертежа. Сплошные тонкие линии вспомогательных построений необходимо сохранить.

Все буквенные и цифровые обозначения следует выполнять чертежным шрифтом.

 

3.7. Последовательность выполнения построений графического решения задачи 10 [ 1 ]

 

Задача – построить линию пересечения фронтально-проецирующего цилиндра вращения с поверхностью открытого тора.

 

Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата А3 (297×420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу формата рамку оснований надписи.

Левую половину поля чертежа используют для построения исходного чертежа задачи. На расстояние 180 мм от верхней рамки поля чертежа проводят горизонтальную прямую линию и на ней на расстоянии 145 мм от левой рамки чертежа отмечают положение точки 0 – начало отсчета координат. Через точку 0 проводят вертикальную прямую линию, перпендикулярную горизонтальной прямой. Вводят обозначения осей проекций X, Y и Z. Из табл. 8 методических указаний [1] выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности тора и цилиндра вращения.

Ось вращения тора располагается на чертеже перпендикулярно фронтальной плоскости проекций. Ее фронтальная проекция совпадает с положением точки 0, а горизонтальная проекция – с положением оси проекций Y. Числовое значение радиуса производящей окружности R₁ выбирается из табл. 8 в зависимости от номера варианта задачи. Точка К – центр производящей окружности. Поверхность тора ограничена двумя основаниями, одно из которых располагается в горизонтальной плоскости проекций, другое – в профильной.

Осью вращения цилиндра радиусом r является фронтально-проецирующая прямая, проходящая через точку Е. Образующие цилиндра имеют длину, равную 3r, и делятся пополам фронтальной меридиональной плоскостью тора. Исходный чертеж задачи (рис. 183) выполняют сплошными тонкими линиями. Оси вращения, симметрии – штрих-пунктирными линиями.

Графическому решению задачи предшествует анализ расположения заданных геометрических фигур относительно друг друга и плоскостей проекций.

Известно, что линия взаимного пересечения поверхностей вращения представляет собой сложную пространственную кривую, точки которой

 

 

 

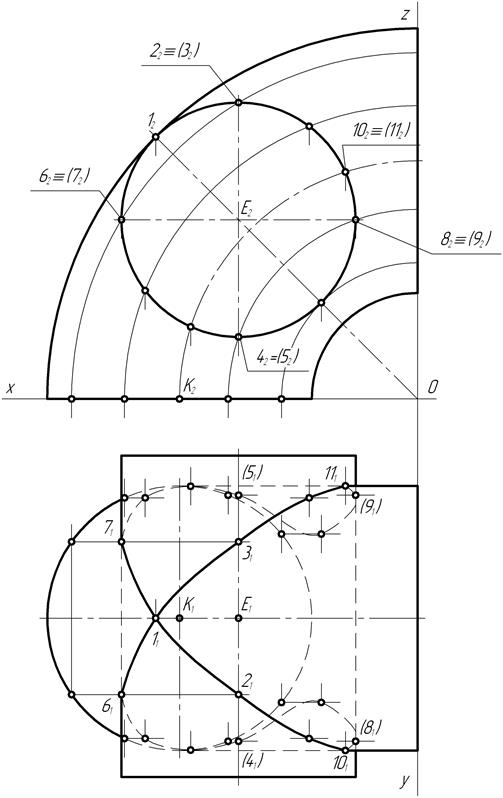
Рис. 183

 

принадлежат обеим фигурам и располагаются только на их наружных поверхностях. По условию задачи цилиндрическая поверхность является фронтально-проецирующей. Поэтому вырожденная фронтальная проекция цилиндра – окружность, является фронтальной проекцией искомой линии взаимного пересечения заданных поверхностей вращения.

Для построения горизонтальной проекции кривой пересечения цилиндра вращения с тором на её фронтальной проекции выделяют положения опорных точек и нескольких произвольных точек.

На фронтальной плоскости проекций отмечают прежде всего положение точки касания поверхностей, если это происходит в результате построения исходного чертежа задачи. Для этого через центры окружностей проводят прямую, которая и выявляет положение на чертеже точки I₂. Проекция I₂ точки касания располагается на главном меридиане тора, а её горизонтальная I₁ проекция – на горизонтальном следе главной меридиональной плоскости. Необходимо отметить, что главная меридиональная плоскость делит поверхности и линию их взаимного пересечения на две симметричные части. В связи с этим часть проекций точек кривой пересечения на фронтальной плоскости проекций будут видимыми, другие – невидимыми. Эти точки являются конкурирующими. Невидимые проекции точек заключают в круглые скобки.

На чертеже выделяют положения точек 2₂, 3₂ и 4₂, 5₂. Эти точки относятся к числу экстремальных точек кривой пересечения. Точки 2₂ и 3₂ – самые высокие, а точки 4₂ и 5₂ – самые низкие. Точки 6₂, 7₂ и 10₂, 11₂ являются точками видимости. Они делят горизонтальную проекцию кривой пересечения на видимую и невидимую части. Остальные точки относятся к числу произвольных. Их фронтальные проекции на чертеже выделяются таким образом, чтобы они располагались на дугах окружностей, проведённых из точки 0.

Построение горизонтальных проекций точек кривой пересечения производится на основании принадлежности их наружной поверхности тора. Каждая из точек поверхности тора совершает вращательное движение вокруг оси его вращения. Траектория вращения представляет собой окружность – параллель. Так как ось вращения тора перпендикулярна фронтальной плоскости проекций, параллель – окружность проецируется на фронтальную плоскость проекций без искажения в натуральную величину, а на горизонтальную плоскость проекций – в прямую линию, параллельную оси проекций X. Каждая из точек поверхности тора вращается вокруг оси по окружности определённого радиуса. Поэтому проекции точки поверхности должны располагаться на соответствующих проекциях этой окружности – параллели. Это свойство и положено в основу графических построений горизонтальных проекций точек кривой пересечения по имеющимся на чертеже их фронтальным проекциям. При этом следует помнить о том, что главная меридиональная плоскость тора делит его поверхность на две симметричные части. В связи с этим горизонтальные проекции точек кривой пересечения располагаются на чертеже симметрично относительно горизонтального следа главной меридиональной плоскости тора.

Соединив плавной лекальной кривой горизонтальные проекции точек в порядке расположения их на фронтальной проекции кривой – окружности цилиндра, получают горизонтальную проекцию кривой взаимного пересечения тора с цилиндром вращения. При этом видимые горизонтальные проекции точек соединяют сплошной толстой линией, невидимые – штриховой линией.

После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку карандашом линий чертежа. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.

Все цифровые и буквенные обозначения следует выполнять чертёжным шрифтом.

 

3.8. Последовательность выполнения построений графического решения задачи 11 [ 1 ]

 

Задача – построить линию пересечения фронтально-проецирующего цилиндра вращения с поверхностью наклонного конуса с круговым основанием.

 

Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата АЗ (297´420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу формата рамку основной надписи. Проводят координатные оси X, Y и Z таким образом, чтобы последующие построения проекций заданных геометрических фигур равномерно располагались бы на поле чертежа. Отмечают положение точки О – начало отсчета координат. Из табл. 9 методических указаний 1 выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности цилиндра вращения и наклонного конуса.

Определяют положения на чертеже проекций К₂, К₁ центра К окружности R основания и вершины S₂ (S₂, S_I) конуса. На фронтальной и горизонтальной плоскостях проекций тонкими штрихпунктирными линиями соединяют одноименные проекции вершины и центра окружности основания конуса. Затем на фронтальной плоскости проекций соединяют проекцию S₂ вершины конуса с крайними точками проекции окружности основания. Получают фронтальную проекцию конуса. На горизонтальной

 

 

 

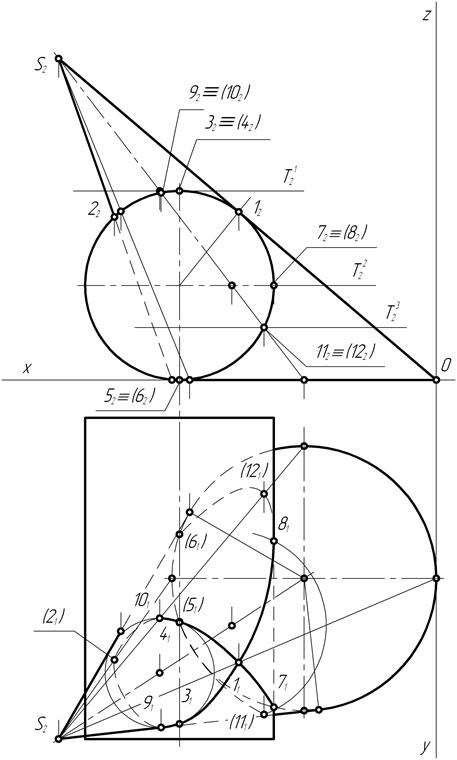
Рис. 184

 

 

плоскости проекций вначале вычерчивают тонкой сплошной линией окружность основания конуса, а затем через точку S₁ проводят прямые, касательные к этой окружности. Получают горизонтальную проекцию наклонного конуса.

Построение проекций фронтально-проецирующего цилиндра не вызывает затруднений. На исходный чертеж задачи не следует наносить координатные размеры заданных геометрических фигур.

В связи с тем, что по условию задачи поверхность цилиндра вращения является проецирующей, на чертеже задачи (рис. 184) уже имеется одна (фронтальная) проекция линии взаимного пересечения поверхностей. Ее фронтальная проекция располагается на окружности – вырожденной проекции цилиндра, находящейся внутри контура фронтальной проекции наклонного конуса.

Известно, что линия взаимного пересечения поверхностей вращения представляет собой сложную пространственную кривую, точки которой принадлежат обеим фигурам. Построение горизонтальных проекций точек кривой взаимного пересечения заданных геометрических фигур возможно лишь на основании признака принадлежности их поверхности наклонного конуса с круговым основанием.

Это предопределяет использование в качестве вспомогательных секущих плоскостей горизонтальных плоскостей уровня. Именно такие секущие плоскости пересекают поверхность наклонного конуса по окружностям – геометрически простым линиям, параллельным основанию. Окружность сечения на горизонтальную плоскость проекций проецируется без искажения в натуральную величину.

Фронтальная проекция этой окружности сечения представляет собой прямую линию, параллельную оси проекций X и расположенную внутри контура фронтальной проекции наклонного конуса. Натуральная величина диаметра окружности сечения ограничивается точками пересечения горизонтальной секущей плоскости с фронтальной проекцией контура наклонного конуса. Центр окружности сечения располагается на фронтальной проекции оси вращения конуса. Соответственно горизонтальная проекция центра окружности сечения располагается на горизонтальной проекции оси вращения конуса. Проекция точки, через которую проведена вспомогательная горизонтальная секущая плоскость, располагается на соответствующих проекциях окружности сечения.

На фронтальной проекции кривой пересечения отмечают положения опорных и нескольких произвольных точек. Вначале отмечают положения точек взаимного пересечения контуров фронтальных проекций заданных геометрических фигур – точки 1₂, 2₂ и 7₂, 8₂. Затем отмечают положения экстремальных точек: 3₂, 4₂ – самых высоких; 7₂, 8₂ – самых правых. Точки 7 и 8 являются одновременно и точками видимости горизонтальной проекции кривой пересечения. Остальные точки, например, 9₂, 10₂ и 11₂, 12₂, относятся к числу произвольных точек кривой.

Построение горизонтальных проекций точек кривой пересечения производят в следующей последовательности:

- на фронтальной плоскости проекций через выбранную проекцию точки кривой пересечения проводят вспомогательную горизонтальную секущую плоскость, например, Т¹ (тау), Т² и т. д.;

- отмечают точку пересечения её с фронтальной проекцией оси вращения конуса. Эта точка является фронтальной проекцией центра окружности сечения;

- при помощи линии связи определяют положение горизонтальной проекции центра окружности сечения на горизонтальной проекции оси вращения конуса;

- строят горизонтальную проекцию окружности сечения и при помощи линии связи определяют положение горизонтальной проекции точки кривой, через фронтальную проекцию которой была проведена вспомогательная горизонтальная секущая плоскость.

Подобным образом получают на чертеже необходимое количество горизонтальных проекций точек кривой пересечения поверхностей.

Соединив плавной лекальной кривой горизонтальные проекции точек в порядке расположения их на фронтальной проекции кривой – окружности цилиндра, получают горизонтальную проекцию кривой пересечения фронтально-проецирующего цилиндра вращения с поверхностью наклонного конуса с круговым основанием. Видимые горизонтальные проекции точек соединяют сплошной толстой линией, невидимые – тонкой штриховой линией.

После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку карандашом линии чертежа. Толстыми сплошными линиями обводят наружный контур проекций фигур. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.

Все цифровые и буквенные обозначения следует выполнять чертёжным шрифтом.

 

3.9. Последовательность выполнения построений графического решения задачи 12 [ 1 ]

 

Задача – построить линию пересечения закрытого тора с
поверхностью наклонного цилиндра вращения.

 

Построение исходного чертежа выполняют в правой половине поля чертежа задачи 10, расположив оси проекции так, чтобы свободное поле

 

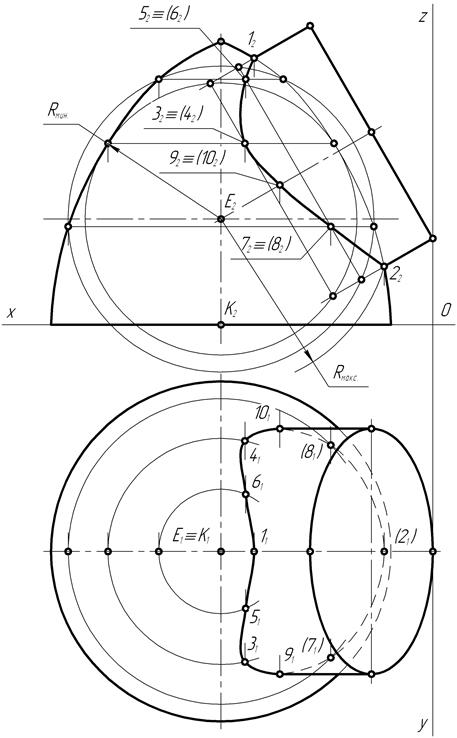
Рис. 185

 

чертежа было рационально использовано фронтальными и горизонтальными проекциями заданных поверхностей.

Из табл. 10 методических указаний 1 выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности вращения.

Вначале строят фронтальную К₂ и горизонтальную К₁ проекции точки К центра окружности R основания тора. Эта окружность представляет собой экваториальную параллель тора, располагающуюся непосредственно в горизонтальной плоскости проекций. Поэтому её фронтальная проекция представляет собой прямую линию, совпадающую с осью проекций X. Строят фронтальную и горизонтальную проекции этой параллели и проводят на чертеже фронтальную проекцию оси вращения тора. Затем строят на фронтальной плоскости проекций главный меридиан тора, представляющий собой замкнутую линию, состоящую из двух пересекающихся на оси вращения дуг окружностей радиуса 2R и отрезка прямой – проекции экваториальной параллели.

На фронтальной плоскости проекций определяют положение фронтальной Е₂ проекции точки Е пересечения вертикальной оси тора с наклонной осью цилиндра вращения радиуса r = 2R/3. Ось цилиндра вращения пересекается с осью поверхности тора в точке Е под углом σ^о, различным для каждого из вариантов задачи. Основание цилиндра вращения касается профильной плоскости проекций. С учётом этих особенностей расположения пересекающихся поверхностей вращения строят их фронтальные и горизонтальные проекции (рис. 185). Построение проекций кривой пересечения производят по точкам, принадлежащим обеим поверхностям вращения.

Представленные на чертеже поверхности вращения имеют общую фронтальную плоскость симметрии, совпадающую с положением их главной меридиональной плоскости. Это обстоятельство позволяет определить на чертеже положения двух опорных точек кривой пересечения.

На фронтальной плоскости проекций в пересечении главных меридианов выявляются положения двух проекций 1₁ и 2₁ точек, принадлежащих каждой из поверхности вращения. Их горизонтальные 1₁ и 2₁ проекции располагаются на следе главной меридиональной плоскости. Одна из них является высшей, а другая – низшей экстремальными точками кривой пересечения.

Так как ни одна из заданных поверхностей не является проецирующей, положение других точек пересечения кривой определяют с помощью либо вспомогательных секущих плоскостей, либо вспомогательных секущих сфер. Способ вспомогательных секущих плоскостей использовать в данном случае не представляется возможным, так как нельзя обе поверхности пересечь одной плоскостью и получить в сечении геометрически простые линии – окружности или прямые. Так как заданные поверхности имеют общую фронтальную плоскость симметрии и оси вращения пересекаются, применяется способ вспомогательных секущих концентрических сфер.

Точка E₂ пересечения фронтальных проекций осей вращения является центром секущих сфер. Максимальный радиус секущей сферы равен наибольшему расстоянию центра сфер до точек пересечения главных меридианов поверхностей вращения. Минимальный радиус секущей сферы равен наибольшему радиусу окружности, вписанной в одну из поверхностей вращения.

Из точки Е₂ пересечения фронтальных проекций осей вращения поверхностей проводят последовательно ряд сфер радиусом, меньшим максимального, но большим минимального. Каждая из сфер пересекает обе поверхности вращения по окружностям. Их фронтальные проекции представляют собой отрезки прямых, соединяющие точки пересечения окружности секущей сферы с главными меридианами поверхностей. В пересечении этих отрезков прямых и находятся фронтальные проекции точек, например, 3₂…8₂, принадлежащих обеим поверхностям.

Подобным образом определяют на чертеже положения фронтальных проекций некоторого количества промежуточных (случайных) точек кривой пересечения.

Горизонтальные проекции точек кривой пересечения поверхностей строят при помощи параллелей закрытого тора.

Соединив плавной лекальной кривой одноимённые проекции точек с учётом их видимости на чертеже, получают фронтальную и горизонтальную проекции линии пересечения закрытого тора с поверхностью наклонного цилиндра вращения.

В пересечении фронтальных проекций кривой и оси вращения цилиндра определяют положения точек 9₂ и 10₂ видимости горизонтальной проекции кривой пересечения.

Видимые проекции точек кривой пересечения соединяют сплошной толстой линией, невидимые – штриховой линией.

Производят окончательную обводку карандашом линий чертежа. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.

Все цифровые и буквенные обозначения следует выполнять чертежным шрифтом.

Литература

Основная

 

1. Гордон В.О. Курс начертательной геометрии: учеб. пособие для студентов вузов / В.О. Гордон, М.А. Семенцов-Огиевский; под ред. В.О. Гордона, Ю.Б. Иванова. 25-е изд., стереотип. – М.: Высшая школа, 2003. – 272 с.

2. Гордон В.О. Сборник задач по курсу начертательной геометрии: учеб. пособие / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. Ю.Б. Иванова. – 9-е изд., стереотип. – М.: Высшая школа, 2003. –
320 с.

3. Инженерная графика: в 3 кн. Кн. 1. Начертательная геометрия. Геометрическое проекционное черчение: учебник / П.Н. Учаев, В.И. Якунин, С.Г. Емельянов и др. – М.: Высшая школа, 2007. – 687 с.

4. Иванов Г.С. Начертательная геометрия: учебник для вузов / Г.С. Иванов. – М.: Машиностроение, 1995. – 224 с.

5. Нартова Л.Г. Начертательная геометрия: учеб. пособие для студентов техн. спец. вузов / Л.Г. Нартова, В.И. Якунин. – М.: Издат. центр «Академия», 2005. – 288 с.

 

Дополнительная

 

6. Локтев О.В. Краткий курс начертательной геометрии: учебник / О.В. Локтев. – М.: Высшая школа, 2006. – 136 с.

7. Локтев О.В. Задачник по начертательной геометрии: учеб. пособие / О.В. Локтев, П.А. Числов. – М.: Высшая школа, 2004. – 104 с.

8. Григорьев В.Г. Инженерная графика: учебник для вузов / В.Г. Григорьев, В.И. Горячев, Т.П. Кузнецова. – М.: Мир Автокниг, 2007. – 464 с.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ …………………………………………………………………..3

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ПРЯМОЙ И ПЛОСКОСТИ……………………………………………………………….4

1.1. Положение прямой в пространстве и её комплексные чертежи………………………………………………………...………...4

1.1.1. Общие сведения………………………………...…………………4

1.1.2. Построение проекций прямой общего положения……………..5

1.1.3. Построение проекций прямых уровня………………………......8

1.1.4. Построение проекций проецирующих прямых………………..12

Вопросы для самопроверки……………………………………………..16

1.2. Положение плоскости в пространстве и её комплексные чертежи…...……………………………………………………............17

1.2.1. Способы задания плоскости на чертеже…………………...….17

1.2.2. Проецирующие плоскости……………………...…..………..…19

1.2.3. Плоскости уровня………………………………………….……23

1.2.4. Плоскости общего положения………...………………………..26

Вопросы для самопроверки……………………………………….…….27

1.3. Взаимное положение прямой и плоскости……………….……28

1.3.1. Принадлежность прямой и точки плоскости……………….….28

1.3.2. Прямая наибольшего наклона плоскости…….………………..29

1.3.2.1. Определение натуральной величины угла наибольшего
                наклона плоскости к плоскостям проекций…………………..30

1.3.3. Параллельность прямой плоскости…………….……………....31

1.3.4. Пересечение прямой с плоскостью…………………………….32

1.3.4.1. Пересечение прямой общего положения с

              проецирующей плоскостью……………………………………32

1.3.4.2. Пересечение проецирующей прямой с плоскостью

общего положения………………………………...…………….33

1.3.4.3. Пересечение прямой общего положения с плоскостью

общего положения……………………………..………………..34

1.3.5. Определение видимости проекций  прямой и плоскости…….35

1.3.6. Перпендикулярность прямой плоскости………………………36

Вопросы для самопроверки…………………………………………..…39

1.4. Последовательность выполнения построений графического

решения задачи 1/1/………...……………………….……….….40

1.4.1. Построение исходного чертежа задачи…………………….…..40

1.4.2. Построение проекций линии пересечения треугольников…...40

1.4.3. Определение видимости проекций треугольников………...….46

1.4.4. Определение натуральной величины треугольника ABC…….49

 

1.5. Многогранные поверхности………………………………….…56

1.5.1. Образование многогранных поверхностей и построение их комплексных чертежей…………………………………….……56

1.5.2. Определение видимости проекций ребер многогранника……59

1.5.3. Принадлежность точки и прямой многогранной

поверхности……………………………………………………...61

1.5.4. Пересечение многогранника с прямой и плоскостью.

Общие положения……………………………………………….62

1.5.4.1. Пересечение многогранника с проецирующей плоскостью….63

1.5.4.2. Пересечение многогранника с прямой. Общие положения......64

1.5.4.3. Пересечение многогранника с проецирующей прямой………65

1.5.4.4. Пересечение многогранника с прямой общего положения…..67

1.5.4.5. Пересечение многогранника с плоскостью общего положения….68

Вопросы для самопроверки………………………………………………75

1.6. Взаимное пересечение многогранных поверхностей.
               Общие положения……………………………………………….76

1.6.1. Взаимное пересечение пирамидальных и призматических поверхностей………………………………………………………77

Вопросы для самопроверки………………………………………………84

1.7. Последовательность выполнения построения графического

решения задачи 3 /1/…………………………….………………85

1.7.1. Построение исходного чертежа задачи………………………..85

1.7.2. Построение проекций линии пересечения многогранников…90

1.8. Построение разверток многогранных поверхностей.

Общие положения………………………………………………96

1.8.1. Построение разверток пирамидальных поверхностей……….96

1.8.2. Построение развертки призматической поверхности

способом нормального сечения………………………………105

1.8.3. Построение развертки призматической поверхности

способом раскатки…………………………………………….110

1.9. Последовательность выполнения построений графического

решения задачи 4 /1/…………………………………………...114

2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ

ВРАЩЕНИЯ С ПРЯМОЙ И ПЛОСКОСТЬЮ…………………………121

2.1. Способы образования и задания на чертеже поверхностей
                вращения……………………………………………………….121

2.2. Принадлежность точки поверхности вращения……………..133

Вопросы для самопроверки…………..…………………………………142

2.3. Пересечение поверхностей вращения с плоскостью.

Общие положения……………….…………………………….144

 

2.4. Пересечение поверхностей вращения с плоскостями

частного положения……………………………………………151

Вопросы для самопроверки……..……………………………………..172

2.5. Пересечение поверхностей вращения с прямой.

Общие положения……………………………………………...174

2.5.1. Пересечение поверхностей вращения с проецирующей прямой………………………………………………………………176

2.5.2. Пересечение поверхностей вращения с прямой уровня……..178

Вопросы для самопроверки………………………..…………………..187

2.6. Последовательность выполнения построений графического

решения задачи 6 /1/………………………………..………….188

3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ВЗАИМНОГО ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ…………………..………………………………………….192

3.1. Взаимное пересечение поверхностей вращения.

Общие положения…………………………………………..…192

3.2. Построение проекций линии взаимного пересечения

поверхностей вращения способом вспомогательных

секущих плоскостей…………………………………………...193

3.3. Построение проекций линии взаимного пересечения

поверхностей вращения способом вспомогательных

секущих сфер. Общие положения…………………………....202

3.3.1. Построение проекций линии взаимного пересечения поверхностей вращения способом концентрических

секущих сфер…………………………………………………..203

3.3.2. Построение проекций линии взаимного пересечения поверхностей вращения способом эксцентрических

секущих сфер…………………………………………………..210

3.4. Особые (частные) случаи взаимного пересечения

поверхностей вращения.............................................................216

3.4.1. Пересечение поверхностей вращения с проецирующей поверхностью вращения………………………………….…………...216

3.4.2. Взаимное пересечение поверхностей вращения двойного соприкосновения…………………………………………………219

Вопросы для самопроверки…………………………………………....221

3.5. Последовательность выполнения построений графического

решения задачи 8 /1/………………………………………..….223

3.6. Последовательность выполнения построений графического

решения задачи 9 /1/………………………………………...…226

3.7. Последовательность выполнения построений графического

решения задачи 10 /1/……………………………………….…229

 

3.8. Последовательность выполнения построений графического

решения задачи 11 /1/……………………………………….…232

3.9. Последовательность выполнения построений графического

решения задачи 12 /1/…………………………………….……235

ЛИТЕРАТУРА…………………..…………………………………………...239

 

 

Учебное издание

 

ЗАЙЦЕВ Юрий Александрович

 

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.

РЕШЕНИЕ ЗАДАЧИ

Учебное пособие

 

Компьютерная верстка Н.В. Полянская, А.Г. Землянка

Редактор О.А. Панина

 

Подписано в печать                                     Формат 60х84 1/16

    Бум. офсет.            Усл. печ. л.        Уч.-изд. л.

    Тираж            - экз.      Заказ         С.

 

 

Саратовский государственный технический университет.

410054 г. Саратов, ул. Политехническая, 77.

 

Отпечатано в РИЦ СГТУ. 410054 г. Саратов, ул. Политехническая, 77.

 

Ю.А. Зайцев

 

 

Начертательная геометрия.

 

РЕШЕНИЕ ЗАДАЧ

 

 

Рекомендовано

научно-методическим советом по начертательной геометрии, инженерной и компьютерной графике Министерства образования и науки РФ в качестве учебного пособия для студентов технических специальностей вузов

 

 

Саратов – 2008

УДК 515.6

ББК 3-17

К65

 

Рецензенты:

Доктор технических наук, профессор Якунин В.И.
Московского государственного технического университета (МАИ)

Доктор технических наук, профессор Горшков Г.Ф.
Московского государственного института радиотехники, электроники и автоматики (технического университета)

 

 

Одобрено

редакционно-издательским советом
Саратовского государственного технического университета

 

 

Зайцев Ю.А.

Начертательная геометрия. Решение задач: учеб. пособие /
Ю.А. Зайцев. Саратов: Сарат. гос. техн. ун-т, 2007. 242 с.

ISBN 978-5-7433-

 

 

Содержит … чертежи и рисунки, довольно подробно иллюстрирующие динамику выполнения построений графического решения типовых задач.

 

Предназначается для студентов машиностроительных специальностей. В учебном пособии рассматриваются основные теоретические положения курса начертательной геометрии, применяемые в практике графического решения метрических и позиционных задач. При изложении теоретических положений использована методика преподавания курса в Саратовском государственном техническом университете.

 

 

УДК 515.6

ББК 3-17

 

  Ó Саратовский государственный

технический университет, 2007

ISBN 978-5-7433-                                           Ó Зайцев Ю.А., 2007

Введение

Студенты, изучающие курс начертательной геометрии, зачастую испытывают значительные затруднения не только в освоении теоретического курса, но и в практике решения типовых метрических и позиционных задач.

Это объясняется, с одной стороны, пробелами в школьной графической подготовке, а, с другой стороны, рисунки, поясняющие те или иные теоретические или графические решения конкретных задач, являются лишь конечным результатом выполнения целого ряда построений, последовательность выполнения которых довольно трудно проследить от начала до конца.

Целью настоящего учебного пособия является систематизация основных теоретических положений курса начертательной геометрии, соответствующих рабочей программе для студентов технических специальностей очной и заочной формы обучения, представление рекомендаций в практике выполнения построений при графическом решении типовых задач.

Начертательная геометрия способствует развитию у студентов пространственного воображения, без которого сдерживается получение оптимальных решений при проектировании. При конструировании сложных технических поверхностей методы начертательной геометрии позволяют получать рациональные изображения изделий.

Учебное пособие содержит конспекты лекций с вопросами для самопроверки по основным разделам курса начертательной геометрии и примеры выполнения построений графического решения типовых задач. Чертежи и рисунки пособия довольно подробно иллюстрирует динамику выполнения графических построений, что, несомненно, будет способствовать более глубокому усвоению студентами основного теоретического материала курса и значительно облегчит им практику графического решения задач по начертательной геометрии.

Более детальное ознакомление с теми или иными теоретическими положениями или доказательствами курса начертательной геометрии можно получить из источников, указанных в перечне рекомендуемой литературы.

Автор приносит искреннюю благодарность профессорам: В.С. Полозову, В.И. Якунину, Г.С. Иванову, Г.Ф. Горшкову; доцентам: А.Н. Кравцову, В.С. Потоцкому за замечания и советы, направленные на улучшение содержания учебного пособия.

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО