1
Умение самостоятельно выбирать рациональный способ решения квадратных уравнений и неравенств, преобразовывать алгебраические дроби, оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия.
Итоговое повторение. 5 часов
Цели ученика:
Провести самоанализ знаний, умений и навыков, полученных и приобретенных в курсе алгебры за 8 класс при обобщающем повторении тем: «Алгебраические дроби», «Квадратные уравнения», «Неравенства».
Для этого необходимо овладеть умениями:
– использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования несложных практических ситуаций на основе изученных формул и свойств тел;
– вычислять площади поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Цели педагога:
· обобщить и систематизировать курс алгебры за 8 класс, решая с учащимися задания повышенной сложности по всему курсу алгебры;
· добиться понимания учащимися возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни;
· сформировать умение интегрировать в личный опыт новую, в том числе самостоятельно полученную информацию.
Алгебраические дроби.
Умение
- применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении, находить значение дроби при заданном значении переменной, преобразовывать тройки алгебраических дробей к дроби с одинаковыми знаменателями, раскладывать числитель
и знаменатель дроби на простые множители несколькими способами, выполнять учебное задание на основе комбинирования ранее изученных алгоритмов и способов действия.
-преобразовывать рациональные выражения, используя все действия с алгебраическими дробями, участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение, доказывать тождества, решать рациональные уравнения, решать задачи, выделяя три этапа математического моделирования, использовать для решения познавательных задач справочную литературу, решать нетиповые задачи, выполняя продуктивные действия эвристического типа.
Квадратные уравнения. Решение задач с помощью квадратных уравнений.
Умение
-решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант, решать задачи на составление квадратных уравнений, давать оценку информации, фактам, процессам, определять их актуальность, находить и использовать информацию, выполнять учебное задание на основе комбинирования ранее изученных алгоритмов и способов действия;
- применять теорему Виета и обратную теорему Виета, решая квадратные уравнения; не решая квадратного уравнения, вычислять выражения, содержащие корни этого уравнения в виде неизвестных, применяя обратную теорему Виета; находить и использовать информацию; решать нетиповые задачи, выполняя продуктивные действия эвристического типа.
Согласовано на заседании методического Согласовано на заседании методического
объединения учителей математики объединения учителей математики
Протокол №____ от «___»_____2015г. Протокол № ___ от «___»_____ 2016 г.
Руководитель МО:_______ Руководитель МО:________
Календарно-тематическое планирование 9 класс
| №п\п | Наименование темы. |
Кол-во часов. | Дата проведения урока. | Планируемые образовательные результаты | Домашнее задание | Сам. работы | Информационно- методическое обеспечение, ЦОРы | |
| Повторение 8 класса. ( 4 часа) Цели ученика: · повторение понятий: степень многочлена, стандартный вид многочлена, действия над многочленами, формулы сокращенного умножения, функция, виды функций, построение графиков функций; · обобщение единичных знаний в систему: – вынесение общего множителя за скобки, применение формул сокращенного умножения и способа группировки при разложении на множители; – нахождение значения функции по заданному аргументу, построение графика; – решение линейных уравнений, систем линейных уравнений методом подстановки и методом сложения; – отличительные признаки видов функций. Цели педагога: · обобщение и систематизация знаний по основным темам курса 8 класса; · формирование умений логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки; · формирование умений ясно, точно и грамотно выражать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический, графический) и свободно переходить с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства. У ниверсальные учебные действия (УУД): регулятивные: учитывать правило в планировании и контроле способа решения; познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы; коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
| ||||||||
| Действия над многочленами. Формулы сокращенного умножения. Основные методы разложения на множители. | 1 | Знать правила сложения, вычитания дробей с одинаковыми и с разными знаменателями; умножение и деление дробей. Уметь выполнять вычисления, воспроизводить информацию с заданной степенью свернутости, определять понятия, приводить доказательства. | ||||||
| Преобразование числовых и алгебраических выражений. Решение уравнений. | 1 | Уметь использовать формулы корней квадратного уравнения, преобразовывать формулы, заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц, вступать в речевое общение, участвовать в диалоге. | ||||||
| Функция. Виды функций. Построение графиков функций. | 1 | Уметь свободно читать графики, описывать свойства функций по графику, применять приемы преобразования графиков, составлять конспект, проводить сравнительный анализ, сопоставлять, рассуждать. | ||||||
| Математические модели реальных ситуаций. | 1 | Уметь рационально применять формулы корней квадратного уравнения для решения прикладных задач, пользоваться теоремой Виета. | ||||||
| Неравенства. Системы неравенств. (16 часов) Цели ученика: Изучить модуль «Виды неравенств» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о понятиях: линейное, квадратное, рациональное неравенство; область допустимых значений неравенств; · овладеть умениями: – определять область допустимых значений; – решать линейные, квадратные, рациональные неравенства и неравенства с модулем; – решать неравенства методом интервалов. Изучить модуль «Системы рациональных неравенств» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о множествах и операциях над ними, о системе уравнений как математических моделях реальных ситуаций; · овладеть умениями: – выполнять операции над множествами; – находить область допустимых значений системы неравенств; – строить математические модели с помощью системы неравенств. Цели педагога: · формирование представлений о неравенстве, видах неравенств, о способах решения линейных, квадратных, рациональных неравенств; · формирование умения определять область допустимых значений; · помощь в овладении навыками составления математической модели ситуации, описанной в условии задачи, решения задачи с выделением трех этапов математического моделирования; · формирование представлений о множествах, о системах неравенств; · формирование умений производить операции над множествами, решать неравенства; · помощь в овладении умением применять правила объединения, пересечения, дополнения множеств при решении неравенств; · помощь в овладении навыками нахождения общего решения для двух и более неравенств. У ниверсальные учебные действия (УУД): регулятивные: осуществлять итоговый и пошаговый контроль по результату; познавательные: строить речевое высказывание в устной и письменной форме; коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. | ||||||||
| 1. | Входная контрольная работа | 1 |
| |||||
| 2. | Линейные и квадратные неравенства. | 2 | Уметь решать простейшие линейные и квадратные неравенства с одной переменной, отмечать на числовой прямой решение неравенства, аргументировано отвечать на поставленные вопросы. Уметь проводить исследование функции на монотонность, находить и использовать информацию, развернуто обосновывать суждения, приводить доказательство. Уметь решать линейные и квадратные неравенства с одной переменной, содержащие модуль, решать неравенства, используя графики. | С-1 | ||||
| | Рациональные неравенства. | 4 | Иметь представления о решении рациональных неравенств методом интервалов. Знать и применять правила равносильного преобразования неравенств. Уметь решать дробно-рациональные неравенства методом интервалов. | С-2,3 | ||||
| | Множества и операции над ними. | 2 | Знать понятие множества, элементов множества, способы задания. Уметь находить среднее арифметическое, задавать множества различными способами. Уметь находить пересечение, объединение, дополнение множеств. Уметь решать задачи по данной теме, участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение. | С-4 | ||||
| | Системы рациональных неравенств. | 5 | Иметь представление о решении систем рациональных неравенств. Уметь решать системы линейных и квадратных неравенств. Уметь решать двойные неравенства, системы простых рациональных неравенств методом интервалов и графическим методом. Объяснять изученные положения на самостоятельно подобранных конкретных примерах. | С-5,6 | ||||
| 6. | Обобщающий урок. | 1 | Уметь решать системы квадратных неравенств, используя графический метод, знать о способах решения систем рациональных неравенств. Уметь извлекать необходимую информацию из учебно-научных текстов, приводить примеры, подбирать аргументы, формулировать выводы. | |||||
| 7. | Контрольная работа №1 | 1 | Уметь решать рациональные неравенства и системы рациональных неравенств; владеть навыками самоанализа и самоконтроля; уметь оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия. | |||||
| Системы уравнений. ( 14 часов) Цели ученика: Изучить модуль «Методы решения систем рациональных уравнений» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о системе рациональных уравнений, о составлении математической модели; · овладеть умениями: – выполнять равносильные преобразования, решая уравнения и системы уравнений с двумя переменными; – решать уравнения и системы уравнений различными методами: графическим, подстановкой, алгебраического сложения, введения новых переменных; – излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. Изучить модуль «Системы уравнений как математические модели реальных ситуаций» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о видах текстовых задач; · овладеть умениями: – составлять систему уравнений по условию задачи; – анализировать и решать задачи на движение по дороге, по воде, на проделанную работу. Цели педагога: · формирование представлений о системе рациональных уравнений, способе освобождения oт знаменателей, о составлении математической модели; · формирование умений совершать равносильные преобразования, решая уравнения и системы уравнений с двумя переменными; решать уравнения и системы уравнений различными методами: графическим, подстановкой, алгебраического сложения, введения новых переменных; · помощь в овладении умением свободно излагать теоретический материал по теме «Системы уравнений»; · помощь в овладении навыками участия в диалоге, понимания точки зрения собеседника, признания права на иное мнение; · формирование представлений о методах решения задач на движение по дороге, по воде, на проделанную работу; · формирование умений составлять и решать математическую модель; · помощь в овладении умением использовать алгоритм составления системы уравнений по условию задачи. У ниверсальные учебные действия (УУД): регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; познавательные: владеть общим приемом решения задач; коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. | ||||||||
| | Основные понятия. | 2 | Иметь понятие о решении системы уравнений и неравенств, знать равносильные преобразования уравнений и неравенств с двумя переменными. | С-7 | ||||
| | Методы решения систем уравнений. | 4 | Уметь использовать графики при решении систем уравнений. Знать алгоритм метода подстановки и метод алгебраического сложения, метод введения новой переменной, оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия. | С-8,9 | ||||
| | Системы уравнений как математические модели реальных ситуаций. | 6 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь обосновывать суждения, правильно оформлять решения, выбирать из данной информации нужную, воспроизводить теорию с заданной степенью свернутости. | С-10 | ||||
| Обобщающий урок | 1 | Уметь свободно составлять математические модели реальных ситуаций и работать с составленной моделью, отбирать и структурировать материал, пользоваться энциклопедией, математическим справочником, записанными правилами; уметь решать нетиповые задачи, выполняя продуктивные действия эвристического типа. | ||||||
| Контрольная работа №2 | 1 | Уметь решать простые нелинейные системы уравнений с двумя переменными различными методами, объяснять изученные положения на самостоятельно подобранных конкретных примерах, аргументированно отвечать на поставленные вопросы, осмысливать и устранять ошибки. | ||||||
| Числовые функции. (24 часа) Цели ученика: Изучить модуль «Определение числовой функции. Способы задания функции» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о числовой функции, графике числовой функции, об области определения и области значений числовой функции; · овладеть навыками нахождения области определения функции; · овладеть умениями: – задания функции различными способами; – построения графика функции по словесной модели. Изучить модуль «Свойства функции» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о таких фундаментальных понятиях математики, как функция, ее область определения, область значений, о различных способах задания функции: аналитическом, графическом, табличном, словесном; · овладеть умениями: – применять понятия четности и нечетности, ограниченности, непрерывности, монотонности функций; – строить и читать графики функций; – находить наибольшее и наименьшее значения на заданном промежутке, решая практические задачи. Изучить модуль «Функции вида Для этого необходимо: · иметь представление о понятии степенной функции с натуральным показателем, свойствах и графике функции; · овладеть умениями: – определять графики функций с четным и нечетным показателем; – классифицировать и проводить сравнительный анализ; – свободно читать свойства степенных функций и строить графики квадратных функций; – приводить примеры, подбирать аргументы, формулировать выводы; – рассуждать и обобщать, аргументированно отвечать на вопросы собеседников. Цели педагога: · формирование представлений о числовой функции, о графике числовой функции, области определения и области значений функции; · формирование умений строить числовую функцию по словесной модели; · помощь в овладении умением находить область определения числовой функции; · помощь в овладении навыками задания функции различными способами; · формирование представлений о таких фундаментальных понятиях математики, как функция, ее область определения, область значений, о различных способах задания функции: аналитическом, графическом, табличном, словесном; · формирование умений применять понятия четности или нечетности, ограниченности, непрерывности, монотонности функций; строить и читать графики функций; находить наибольшее и наименьшее значения на заданном промежутке, решая практические задачи; · помощь в овладении умением построения графика функции и описания ее свойств; · формирование представлений о понятии степенной функции · формирование умений определять графики функций с четным и нечетным показателем, классифицировать и проводить сравнительный анализ; свободно читать свойства степенных функций и строить графики квадратных функций; приводить примеры, подбирать аргументы, формулировать выводы; рассуждать и обобщать, аргументированно отвечать на вопросы собеседников. У ниверсальные учебные действия (УУД): регулятивные: учитывать правило в планировании и контроле способа решения; познавательные: строить речевое высказывание в устной и письменной форме; коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. | ||||||||
| | Определение числовой функции. Область определения, область значений функции. | 4 | Знать определение числовой функции, области определения, области значений функции. Уметь находить область определения функции, объяснять изученные положения на самостоятельно подобранных конкретных примерах, подбирать аргументы, формулировать выводы. | С-11 | ||||
| | Способы задания функции. | 2 | Иметь представления о способах задания функции: аналитическом, графическом, табличном и словесном. Уметь при задании функции применять эти способы. Уметь приводить примеры, подбирать аргументы, формулировать выводы, отражать в письменной форме свои решения, рассуждать, формулировать вопросы, задачи, создавать проблемную ситуацию. Уметь при задании функции применять различные способы: аналитический, графический, табличный, словесный, отбирать и структурировать материал, проводить анализ данного задания. | С-12 | ||||
| | Свойства функции. | 3 | Иметь представления о свойствах функции: монотонности, н6аибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности. Уметь исследовать функции на: монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность; отбирать и структурировать материал, аргументированно отвечать на поставленные вопросы, участвовать в диалоге, работать с чертежными инструментами. | С-13 | ||||
| | Четные и нечетные функции. | 3 | Иметь представление о четной и нечетной функции, об алгоритме исследования функции на четность и нечетность. Уметь объяснять изученные положения на самостоятельно подобранных конкретных примерах, определять понятия, приводить доказательства; применять алгоритм исследования функции на четность и нечетность, строить графики четных и нечетных функций, приводить примеры, подбирать аргументы, формулировать выводы; умеют классифицировать и проводить сравнительный анализ. | С-14 | ||||
| Контрольная работа №3 | 1 | |||||||
| | Функции вида у=хn. Их свойства и графики. | 4 | Иметь представление о степенной функции с натуральным показателем, свойствах и графике функции. Уметь определять графики с четным и нечетным показателем, классифицировать и проводить сравнительный анализ, рассуждать и обобщать, аргументированно отвечать на вопросы собеседников, свободно читать свойства степенных функций и строить графики квадратных функций. | С-15,16 | ||||
| | Функции у=х-n, их свойства и графики. | 3 | Иметь представление о степенной функции с отрицательным целым показателем, о свойствах и графике функции. Уметь определять графики функций с четным и нечетным отрицательным целым показателем, приводить примеры, подбирать аргументы, формулировать выводы. | С-17 | ||||
| | Функция у= 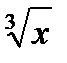 , ее свойства и график. , ее свойства и график.
| 3 | Иметь представления о степенной функции с дробным показателем, о свойствах и графике функции. Уметь определять графики функций с четным и нечетным дробным показателем. Уметь строить графики степенных функций с любым показателем и описывать свойства элементарных функций. | С-18-20 | ||||
| Контрольная работа №4 | 1 | Уметь строить и описывать свойства элементарных функций, владеть навыками самоанализа и самоконтроля, уметь предвидеть возможные последствия своих действий. Уметь оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия. | ||||||
| Прогрессии. (19 часов) Цели ученика: Изучить модуль «Арифметическая прогрессия» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о числовой последовательности, арифметической прогрессии как частном случае числовых последовательностей, · овладеть умениями: – формулировать и обосновывать ряд свойств арифметической прогрессии, сводить их в одну таблицу; – решать текстовые задачи, используя свойства арифметической прогрессии; – выводить характеристическое свойство арифметической прогрессии; – применять eго при решении математических задач. Изучить модуль «Геометрическая прогрессия» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о числовой последовательности, геометрической прогрессии как частном случае числовых последовательностей, · овладеть умениями: – формулировать и обосновывать ряд свойств геометрической прогрессии, сводить их в одну таблицу; – решать текстовые задачи, используя свойства геометрической прогрессии; – выводить характеристическое свойство геометрической прогрессии; – применять его при решении математических задач. Цели педагога: · формирование представлений о числовой последовательности, арифметической прогрессии как частном случае числовых последовательностей, о трех способах задания последовательности: аналитическом, словесном и рекуррентном; · формирование умений обосновывать ряд свойств арифметической прогрессий, сводить их в одну таблицу; решать текстовые задачи, используя свойства арифметической прогрессии; выводить характеристическое свойство арифметической прогрессии и уметь применять его при решении математических задач; · формирование представлений о числовой последовательности, геометрической прогрессии как частном случае числовых последовательностей, о трех способах задания последовательности: аналитическом, словесном и рекуррентном; · формирование умений обосновывать ряд свойств геометрической прогрессии, сводить их в одну таблицу, решать текстовые задачи, используя свойства геометрической прогрессии; выводить характеристическое свойство геометрической профессии и уметь применять его при решении математических задач. У ниверсальные учебные действия (УУД): регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; познавательные: ориентироваться на разнообразие способов решения задач; коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. | ||||||||
| | Числовые последовательности. | 3 | Знать определение числовой последовательности. Уметь задавать числовую последовательность аналитически, словесно, рекуррентно, извлекать необходимую информацию из учебно-научных текстов, развернуто обосновывать суждения, приводить доказательства, в том числе от противного. | С-21 | ||||
| | Арифметическая прогрессия. Основные понятия. Арифметическая прогрессия. Формула n-го члена арифметической прогрессии. Арифметическая прогрессия. Формула суммы членов конечной арифметической прогрессии. Арифметическая прогрессия. Характеристическое свойство арифметической прогрессии. | 1
2
3
1 | Знать формулы n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии, характеристическое свойство арифметической прогрессии. Уметь применять формулы при решении задач, решать проблемные задачи и ситуации, объяснять изученные положения на самостоятельно подобранных конкретных примерах . | С-22-24 | ||||
| | Геометрическая прогрессия. | 8 | Иметь представление о правиле задания геометрической прогрессии, о формуле n-го члена геометрической прогрессии, формуле суммы членов конечной геометрической прогрессии; применяют формулы при решении задач. Уметь применять формулу n-го члена геометрической прогрессии, формулу суммы конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии. | С-25,26 | ||||
| Контрольная работа №5 |
| Уметь решать задания на применение свойств арифметической и геометрической прогрессии; владеют навыками самоанализа и самоконтроля. Умеют оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия. | ||||||
| Элементы комбинаторики, статистики и теории вероятностей. (10 часов) Цели ученика: Изучить модуль «Комбинаторные задачи» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о комбинаторных задачах, элементах комбинаторики: перестановке, перемещении, сочетании; о понятии «среднее арифметическое», размахе ряда чисел, моде ряда чисел, о медиане произвольного ряда; · овладеть умениями: – решать комбинаторные задачи, составляя дерево возможных вариантов, используя комбинаторное правило умножения; – решать задачи на нахождение среднего арифметического, размаха ряда чисел, моды ряда чисел; – осуществлять сбор и группировку статистических данных Изучить модуль «Простейшие вероятностные задачи» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне. Для этого необходимо: · иметь представление о новом математическом направлении – теории вероятностей, о понятии множества и операциях над ними, о простейших вероятностных задачах; · овладеть умениями: – решать вероятностные задачи жизненного содержания; – выводить основные формулы теории вероятностей; – применять формулы теории вероятностей. Цели педагога: · формирование представлений о комбинаторных задачах, элементах комбинаторики: перестановке, перемещении, сочетании; о понятии «среднее арифметическое», размахе ряда чисел, моде ряда чисел, о медиане произвольного ряда; · формирование умений решать комбинаторные задачи, составляя дерево возможных вариантов, используя комбинаторное правило умножения; · помощь в овладении умением решать задачи на нахождение среднего арифметического, размаха ряда чисел, моды ряда чисел; осуществлять сбор и группировку статистических данных · формирование представлений о новом математическом направлении – теории вероятностей, о понятии множества и операциях над ни- · формирование умения выводить основные формулы теории вероятностей; · помощь в овладении умением решать вероятностные задачи жизненного содержания; · помощь в овладении навыком применять формулы теории вероятностей. У ниверсальные учебные действия (УУД): регулятивные: учитывать правило в планировании и контроле способа решения; познавательные: ориентироваться на разнообразие способов решения задач; коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. | ||||||||
| | Комбинаторные задачи. | 2 | Иметь представление о комбинаторных задачах, знать элементы комбинаторики: перестановка, перемещение, сочетание. Уметь решать задачи, составляя дерево всевозможных вариантов, используя правило умножения. | С-27,28 | ||||
| | Статистика-дизайн информации. | 2 | Иметь представление о понятии «среднее арифметическое», размахе ряда чисел, моде ряда чисел. Уметь решать задачи на нахождение среднего арифметического, размаха, моды ряда чисел. Уметь осуществлять сбор и группировку статистических данных, составлять конспект, проводить сравнительный анализ, сопоставлять, рассуждать. | С-29, 30 | ||||
| | Простейшие вероятностные задачи. | 3 | Иметь представление об основных видах случайных событий: достоверное, невозможное, несовместимое события; о событии, противоположном данному событию, о сумме двух случайных событий. Уметь решать простейшие задачи, используя комбинаторное правило умножения; умеют вычислять достоверное, невозможное, несовместимое события, проводить сравнительный анализ, сопоставлять, рассуждать. . | С-31, 32 | ||||
| | Экспериментальные данные и вероятности событий. | 2 | Уметь вычислять событие, противоположное данному событию, и сумму двух случайных событий, свободно применять теоремы, необходимые для решения практических задач, оформлять решения, выполнять перенос ранее усвоенных способов действий в новые условия. | С-33 | ||||
| Контрольная работа №6 | 1 | Уметь свободно применять теоремы, необходимые для решения практических задач, проводить сравнительный анализ, сопоставлять, рассуждать. | ||||||
| Обобщающее повторение курса алгебры за 9 класс. (15 часов) Цели ученика: Изучить модуль «Обобщающее повторение курса алгебры за 9 класс базового уровня» и овладеть содержанием курса на уровне базовой подготовки. Для этого необходимо продемонстрировать: · определенную системность знаний и широту представлений; · владение базовыми алгоритмами, знание и понимание важных элементов содержания (понятий, их свойств, приемов решения задач и прочее); · умение пользоваться различными математическими языками; · умение применить знания к решению математических задач, не сводящихся к прямому использованию алгоритма, а также применение знаний в простейших практических ситуациях. Цели педагога: · обобщить и систематизировать курс алгебры за 9 класс, решая задания базового уровня по всему курсу; · формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни; · формирование умений интегрирования в личный опыт новой, в том числе самостоятельно полученной информации; · помощь в овладении умением применять знания к решению математических задач, не сводящихся к прямому использованию алгоритма, а также применение знаний в простейших практических ситуациях. У ниверсальные учебные действия (УУД): регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; познавательные: проводить сравнение, сериацию и классификацию по заданным критериям; коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. | ||||||||
| Числовые выражения. | 1 | Знать, что такое числовое выражение, числовое значение буквенного выражения, допустимые значения переменных, входящих в алгебраические выражения. Уметь подставить числовое выражение вместо переменных, доказать тождество и совершить преобразования алгебраических выражений. | ||||||
| Алгебраические выражения. | 1 | Уметь: применить свойства степеней с целым показателем в преобразованиях выражений, содержащих степени с целым показателем; выполнять сложение, вычитание и умножение многочленов, используя формулы сокращенного умножения: квадрат суммы и квадрат разности, формулу разности квадратов; формулировать вопросы, задачи, создавать проблемную ситуацию. | ||||||
| Тождественные преобразования алгебраических выражений. | 1 | Уметь разложить многочлен на множители и квадратный трехчлен на линейные множители, сократить дробь и выполнить действие с алгебраическими дробями, объяснить изученные положения на самостоятельно подобранных конкретных примерах. | ||||||
| Функции и их графики. | 1 | Уметь строить и описывать свойства элементарных функций, определять понятия, приводить доказательства, находить и устранять причины возникших трудностей, свободно использовать графики элементарных функций и описывать их свойства, решая прикладные задачи, аргументированно отвечать на поставленные вопросы, осмыслять ошибки и устранять их. | ||||||
| Уравнения и системы уравнений. | 1 | Уметь решать уравнения и системы уравнений, свободно пользоваться условиями равносильности при решении уравнений и систем уравнений, решать нелинейные системы уравнений с двумя переменными различными методами, приводить примеры, подбирать аргументы, формулировать выводы. | ||||||
| Неравенства и системы неравенств. | 1 | Уметь решать неравенства и системы неравенств, свободно пользоваться условиями равносильности при решении неравенств и систем неравенств, решать линейные системы неравенств с двумя переменными различными способами, объяснять изученные положения на самостоятельно подобранных конкретных примерах, отбирать и структурировать материал, передавать информацию сжато, полно, выборочно. | ||||||
| Задачи на составление уравнений или систем уравнений. | 1 | Уметь распознавать арифметические и геометрические прогрессии, применять формулы общих членов, суммы n первых членов арифметической и геометрической прогрессий, решая текстовые задачи, выполнять и оформлять тестовые задания, подбирать аргументы для обоснования своей точки зрения. | ||||||
| Последовательности и прогрессии. | 1 | Уметь распознавать арифметические и геометрические прогрессии, применять их свойства, формулы общих членов, суммы n первых членов арифметической и геометрической прогрессий, решая текстовые задачи; извлекать необходимую информацию из учебно-научных текстов, отделять основную информацию от второстепенной, сопоставлять, классифицировать, участвовать в диалоге. | ||||||
| Итоговая контрольная работа |
| |||||||
| Буквенные выражения. | 1 | Знать, что такое буквенное выражение, числовое значение буквенного выражения, допустимые значения переменных, входящих в алгебраические выражения. Уметь подставить выражение вместо переменных, доказать тождество и совершить преобразования алгебраических выражений, привести примеры, подобрать аргументы, сформулировать выводы. | ||||||
| Уравнения и неравенства с параметром. | 2 | Уметь решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы с параметром, воспринимать устную речь, участвовать в диалоге. | ||||||
| Построение графика функции и ее исследование. | 2 | Уметь находить значения функции, заданной формулой, таблицей, графиком, по ее аргументу, определять свойства функции по ее графику, описывать свойства изученных функций, строить их графики, приводить примеры, подбирать аргументы, формулировать выводы. | ||||||
| Элементы статистики и теории вероятностей. | 1 | Уметь приводить примеры случайных событий, решать комбинаторные задачи, применяя перебор вариантов, правило умножения, представлять данные в виде таблиц, диаграмм, графиков. Иметь представление о средних результатах измерений, статистическом выводе на основе выборки, частоте события, вероятности, о равновозможных событиях и подсчетах их вероятности, о геометрической вероятности. | ||||||
Согласовано на заседании методического Согласовано на заседании методического
объединения учителей математики объединения учителей математики
Протокол №____ от «___»_____2015г. Протокол № ___ от «___»_____ 2016 г.
Руководитель МО:_______ Руководитель МО:________
Дата: 2019-02-25, просмотров: 326.
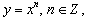 их свойства и графики» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне.
их свойства и графики» и получить последовательную систему математических знаний, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне.