МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1 ИМЕНИ АЛЕКСАНДРА КИРИЛЛОВИЧА ПРОСОЕДОВА
«Согласовано» «Утверждаю»
Зам.директора по УВР: Директор МОУ СОШ №1
_____________
__________________
«___»_________2015 г «____»__________2015г
Рабочая программа
По алгебре для 7-9 классов
(среднее общее образование)
Учитель математики: Шарикова Ирина Евгеньевна
Рассмотрено и обсуждено на заседании Тематическое планирование откорректировано
методического совета Протокол №_______от «_____» ________2016 г.
Протокол №_____ от «___»_________ 2015 г Зам. директора по УВР:
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа основного общего образования по алгебре составлена на основе авторской программы И.И.Зубаревой и А.Г.Мордковича, Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. Настоящая рабочая программа разработана применительно к учебной программе А.Г. Мордковича «Алгебра» для 7-9 -х классов и ориентирована на использование учебно-методического комплекта:
- А.Г. Мордкович Алгебра 7 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010-2013
- А.Г.Мордкович Алгебра 7 класс: метод. Пособие для учителя-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 7 класс: самостоятельные работы-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 7 класс: контрольные работы-М: Мнемозина, 2010-2013
- А.Г. Мордкович Алгебра 8 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010-2013
- А.Г.Мордкович Алгебра 8 класс: метод. Пособие для учителя-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 8 класс: самостоятельные работы-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 8 класс: контрольные работы-М: Мнемозина, 2010-2013
- А.Г. Мордкович Алгебра 9 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010
- А.Г.Мордкович Алгебра 9 класс: метод. Пособие для учителя-М: Мнемозина, 2010
- Л.А.Александрова Алгебра 9 класс: самостоятельные работы-М: Мнемозина, 2010
- Л.А.Александрова Алгебра 9 класс: контрольные работы-М: Мнемозина, 2010
- А.Г.Мордкович Алгебра 7-9 кл.:тесты-М: Мнемозина 2010-2013
- Е.М.Ключникова Рабочая тетрадь по алгебре к учебнику А.Г.Мордковича «Алгебра. 7 класс», «Алгебра. 8 класс».
Представленная программа выполняет две основные функции:
· информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития обучающихся 7-9 классов средствами данного учебного предмета;
· организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации обучающихся.
ОПИСАНИЕ МЕСТА УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
На изучение алгебры согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации на ступени основного общего образования отводится 312 часов из расчёта 3 часа в неделю в течение каждого года обучения. Согласно действующему в школе учебному плану в 7,8-х классах предусмотрено преподавание алгебры в объеме 105 часов, в 9-м классе в объеме 102 часов.
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ ОСНОВНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
1) сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и
самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных
интересов;
2) сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
3) сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и
младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
4) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;ЕБВАНИЯ К РЕЗУЛЬТАТАМ ОБУЧЕНИЯ
5) представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
6) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
7) креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
8) умение контролировать процесс и результат учебной математической деятельности;
9) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
1) умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
2) умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
3) умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
4) осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родо-видовых связей;
5) умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
6) умение создавать, применять и преобразовывать знаково- символические средства, модели и схемы для решения учебных и познавательных задач;
7) умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
8) сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
9) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
10) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
11) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
12) умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
13) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
14) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
15) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
16) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
17) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
1) умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
2) владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
3) умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных НИматематических задач и задач, возникающих в смежных учебных предметах;
4) умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
5) умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
6) овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
7) овладение основными способами представления и анализа статистических данных; умение решать задачи на нахождение частоты и вероятности случайных событий;
8) умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
СОДЕРЖАНИЕ ПРОГРАММЫ КУРСА АЛГЕБРЫ ДЛЯ 7-9 КЛАССОВ
Числовая линия
Натуральные, рациональные, иррациональные и действительные числа. Изображение чисел на числовой прямой. Числовые промежутки: аналитическая и геометрическая модели промежутков, обозначение, название. Принадлежность числа числовому промежутку. Числовые выражения, значения числовых выражений. Оценка иррациональных чисел. Запись рационального числа в виде конечной и бесконечной периодической дроби. Запись конечной и бесконечной периодической дроби в виде обыкновенной. Сравнение чисел, свойства числовых неравенств. Множества и подмножества. Пересечение и объединение множеств.
Арифметические действия на множестве действительных чисел. Понятие квадратного и кубического корня и корня n-ой степени из неотрицательного числа. Возведение действительных чисел в степень, извлечение квадратного и кубического корня из неотрицательного числа. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. Приближенные вычисления. Приближение с избытком, с недостатком. Оценка приближения. Абсолютная и относительная погрешность приближения. Стандартный вид числа, его порядок, арифметические действия с числами стандартного вида.
Алгебраическая линия
Математический язык. Математическая модель. Буквенные выражения, значения буквенных выражений при различных значениях входящих в него букв. Допустимые и недопустимые значения выражений. Степень числа с натуральным показателем, степень числа с нулевым и отрицательным показателем. Свойства степени. Одночлены, стандартный вид одночлена, подобные одночлены, арифметические действия с одночленами, возведение одночлена в степень. Многочлены, стандартный вид многочлена, приведение подобных членов многочлена, арифметические операции с многочленами. Разложение многочленов на множители. Формулы сокращенного умножения. Тождества. Тождественные преобразования многочленов. Алгебраические дроби. Допустимые и недопустимые значения алгебраических дробей. Основное свойство алгебраической дроби. Сокращение дробей. Приведение алгебраических дробей к общему знаменателю. Арифметические действия с алгебраическими дробями. Степень дроби. Преобразования алгебраических дробей. Степень с целым показателем. Понятие квадратного корня из неотрицательного выражения, его свойства. Вынесение множителя за знак радикала. Внесение множителя под знак радикала. Преобразование выражений, содержащих квадратный корень. Линейные, квадратные, рациональные и иррациональные уравнения, алгебраические уравнения, сводимые к квадратным. Линейные, квадратные и рациональные неравенства. Системы уравнений и неравенств. Уравнения и неравенства как математические модели реальных ситуаций. Системы уравнений и неравенств как математические модели реальных ситуаций.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ КУРСА АЛГЕБРЫ В 7—9 КЛАССАХ
РАЦИОНАЛЬНЫЕ ЧИСЛА
Выпускник научится:
1) понимать особенности десятичной системы счисления;
2) владеть понятиями, связанными с делимостью натуральных чисел;
3) выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
4) сравнивать и упорядочивать рациональные числа;
5) выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применять калькулятор;
6) использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Выпускник получит возможность:
7) познакомиться с позиционными системами счисления
с основаниями, отличными от 10;
8) углубить и развить представления о натуральных числах и свойствах делимости;
9) научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Выпускник научится:
1) использовать начальные представления о множестве действительных чисел;
2) владеть понятием квадратного корня, применять его в вычислениях.
Выпускник получит возможность:
3) развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
4) развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
ИЗМЕРЕНИЯ, ПРИБЛИЖЕНИЯ, ОЦЕНКИ
Выпускник научится использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
1) понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
2) понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Выпускник научится:
1) владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
2) выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
3) выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
4) выполнять разложение многочленов на множители.
Выпускник получит возможность:
5) научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
6) применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
УРАВНЕНИЯ
Выпускник научится:
1) решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;
2) понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
3) применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Выпускник получит возможность:
4) овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
5) применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
НЕРАВЕНСТВА
Выпускник научится:
1) понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
2) решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
3) применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
4) разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
5) применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
Выпускник научится:
1) понимать и использовать функциональные понятия и язык (термины, символические обозначения);
2) строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
3) понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
4) проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
5) использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Выпускник научится:
1) понимать и использовать язык последовательностей (термины, символические обозначения);
2) применять формулы, связанные с арифметической и геометрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Выпускник получит возможность научиться:
3) решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;
4) понимать арифметическую и геометрическую прогрессии как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
КОМБИНАТОРИКА
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.
Содержание курса «Алгебра-7»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Математический язык. Математическая модель Числовые и алгебраические выражения. Что такое математический язык и математическая модель. Линейное уравнение с одной переменной. Линейное уравнение с одной переменной как математическая модель реальной ситуации. Координатная прямая. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Вычисление значений числовых выражений, применение свойств и правил арифметических действий, выбор рациональных способов вычислений. Чтение выражений, формул, правил, записанных на математическом языке, перевод словесных формулировок на математический язык. Использование символики для записи математических утверждений. Работа в паре и группе. Участие в деловой игре. Описание реальных ситуаций с помощью математических моделей. Планирование хода решения задач с использованием трех этапов математического моделирования. Прогнозирование результата решения, оценка реальности полученного ответа. Применение алгоритма при решении линейного уравнения. Изображение чисел и числовых промежутков на числовой прямой. Чтение учебника, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму. Подведение итогов. Самооценка знаний. | Умение составлять числовые и буквенные выражения, записывать математические свойства, правила, формулы на математическом языке; осуществлять числовые подстановки в алгебраические выражения и формулы и выполнять соответствующие вычисления; выражать из формулы одну переменную через другие; находить область допустимых значений переменных в выражении. Умение распознавать и решать линейные уравнения и уравнения, сводящиеся к ним; решать текстовые задачи алгебраическим методом: описывать реальную ситуацию в виде математической модели – линейного уравнения, решать полученное уравнение и интерпретировать результат. Умение изображать числа и числовые промежутки на координатной прямой, определять принадлежность точки данному числовому промежутку. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
| Линейная функция Координатная плоскость. Линейное уравнение с двумя переменными. Линейная функция. Взаимное расположение графиков линейных функций. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Построение точек и геометрических фигур в координатной плоскости. Построение прямой, заданной линейным уравнением с двумя переменными. Моделирование реальной ситуации с помощью линейного уравнения с двумя переменными. Исследование графической модели с точки зрения реальности результата. Проведение аналогии между линейным уравнением с двумя переменными и линейной функцией. Работа в паре и в группе. Построение графика линейной функции, в том числе на заданном промежутке. Чтение графика, нахождение наибольшего и наименьшего значений функции. Анализ поведения графика линейной функции в зависимости от значений коэффициентов k и m на основе наблюдения и сравнения. Работа в группе. Исследование взаимного расположения графиков линейных функций. Работа в группе. Самостоятельное изучение материала учебника, извлечение учебной информации, осмысление ее и применение в учебной деятельности. Выполнение упражнений по аналогии, алгоритму, образцу. Самоконтроль решения. Участие в мини проектной деятельности «Линейная функция как модель описания реальных ситуаций». Поиск, обнаружение и устранение ошибок при построении графиков линейного уравнения с двумя переменными и линейной функции. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Умение строить на координатной плоскости точки и фигуры по заданным координатам, фигуры, симметричные данным относительно координатных осей и начала координат, а также определять координаты точек, данных на координатной плоскости. Первоначальные умения записывать уравнения прямых, параллельных координатным осям. Понимание, что такое линейное уравнение с двумя переменными. Умение узнавать указанные уравнения, выражать в них одну переменную через другую, определять, является ли пара чисел решением уравнения с двумя переменными. Умение строить прямую, которая является графиком данного линейного уравнения с двумя переменными.
Понимание, что такое линейная функция, что такое независимая переменная – аргумент, зависимая переменная – функция. Знание способов задания функции формулой и графически, умение составлять таблицы значений функции. Умение строить и читать графики линейной функции, находить по графику значение одной переменной по значению другой, определять наименьшее и наибольшее значения функции, решать графически линейные уравнения и неравенства. Умение показывать схематически положение на координатной плоскости графиков функций 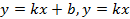 в зависимости от значений коэффициентов k и b.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение осуществлять проектную деятельность: ставить цель, собирать и представлять информацию.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. в зависимости от значений коэффициентов k и b.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение осуществлять проектную деятельность: ставить цель, собирать и представлять информацию.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации.
|
| Системы двух линейных уравнений с двумя переменными Основные понятия о системах двух линейных уравнений с двумя переменными. Методы решения систем двух линейных уравнений с двумя переменными: графический, подстановки и алгебраического сложения. Системы двух линейных уравнений как математические модели реальных ситуаций. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Изучение новой математической модели – системы двух линейных уравнений с двумя переменными. Проведение аналогии между взаимным расположением двух прямых на координатной плоскости и графическим методом решения систем двух линейных уравнений с двумя переменными. Составление алгоритма решения систем графическим методом. Исследование систем уравнений на предмет числа решений с помощью функционально-графических представлений. Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения систем (точка пересечения неточна или слишком удалена). Работа в группе. Составление алгоритма решения систем методом постановки и алгебраического сложения. Работа в паре. Выполнение самоконтроля при решении систем. Поиск, обнаружение и устранение ошибок при решении систем. Описание реальных ситуаций с помощью систем двух линейных уравнений с двумя переменными. Решение задач в три этапа математического моделирования. Участие в мини проектной деятельности «Моделирование реальных ситуаций с помощью систем линейных уравнений». Отыскание информации на заданную тему в учебнике. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание того, что такое система двух линейных уравнений с двумя переменными. Умение узнавать указанные системы, определять, является ли пара чисел решением системы двух линейных уравнений с двумя переменными. Умение решать системы двух линейных уравнений с двумя переменными графическим методом, использовать функционально-графические представления для исследования систем уравнений на предмет числа решений. Умение решать системы двух линейных уравнений с двумя переменными методом подстановки и алгебраического сложения. Умение решать текстовые задачи алгебраическим методом, составляя математическую модель задачи в виде системы двух линейных уравнений с двумя переменными, решать полученную систему и интерпретировать результат. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность взаимодействовать с товарищами по классу в деловой ситуации. |
| Степень с натуральным показателем и ее свойства Понятие степени с натуральным показателем и ее свойства. Умножение и деление степеней с одинаковым показателем. Степень с нулевым показателем. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Чтение и запись степени выражения, свойств степени на математическом языке. Составление таблицы степеней. Изучение по учебнику этапов теоретического исследования. Самостоятельное проведение исследования. Доказательство свойств степени. Конструирование предложений с помощью связок «если…, то…». Работа в паре. Применение определения и свойств степени при решении простейших уравнений, моделирование реальных ситуаций, приводящих к простейшему степенному уравнению. Мини проект. Осуществление самоконтроля решения, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Знание определения степени с натуральным показателем и ее свойств, умение вычислять степень числа. Знание табличных значений степеней 2, 3, 5, 10. Понятие степени с нулевым показателем. Умение применять свойства степени для преобразования выражений и вычислений. Умение конструировать математические предложения с помощью связок «если…, то…», воспроизводить несложные доказательства изученных теорем о свойствах степени с натуральным показателем. Умение решать простейшие уравнения, используя определение степени с неотрицательным целым показателем. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Первичное умение проводить доказательство утверждения. Умение выполнять действия по правилу и образцу. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Одночлены. Арифметические операции над одночленами Понятие одночлена. Стандартный вид одночлена. Сложение и вычитание одночленов. Умножение одночленов. Возведение одночленов в натуральную степень. Деление одночлена на одночлен. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное чтение учебника с целью поиска информации на заданную тему. Выполнение алгебраических преобразований с одночленами, пошаговый контроль правильности выполнения алгоритма преобразования. Работа в паре. Сравнение двух дробей по виду и выявление, которая из них является одночленом, а которая нет, обоснование вывода. Составление алгоритма приведения одночлена к стандартному виду, сложения одночленов. Работа в паре. Выполнение действий с одночленами. Описание реальных ситуаций с помощью модели (уравнения) с подобными одночленами. Решение задач в три этапа математического моделирования. Мини проект. Наблюдение и вывод, в каком случае один одночлен можно разделить на другой одночлен и как это сделать. Выполнение заданий, связанных с выявлением некорректных высказываний. Самоконтроль выполнения действий и преобразований с одночленами, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание, что такое одночлен. Умение записывать одночлены в стандартном виде, умение приводить одночлены к стандартному виду. Умение выполнять сложение и вычитание подобных одночленов, умножение одночленов, возведение одночлена в степень, деление одночлена на одночлен в корректных случаях. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить наблюдение, сравнивать, анализировать ситуацию, делать выводы. Умение работать по правилу и образцу. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Многочлены. Арифметические операции над многочленами Понятие многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника, связанной с изучением нового материала. Выполнение действий с многочленами по правилам. Работа в паре. Описание реальных ситуаций с помощью математической модели, представляющей собой многочлены. Решение задач в три этапа математического моделирования. Мини проект. Вывод формул сокращенного умножения. Чтение их и запись на математическом языке. Применение геометрической модели, иллюстрирующей вывод формул разности квадратов и квадрата суммы и разности. Выполнение преобразований многочленов, пошаговый контроль правильности и полноты выполнения алгоритма. Поиск, обнаружение и устранение арифметических и алгебраических ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Понимание, что такое многочлен. Умение записывать многочлены в стандартном виде, умение выполнять сложение и вычитание многочленов, умножение многочлена на одночлен, умножение многочлена на многочлен. Умение применять правило умножения многочленов для выведения формул разности квадратов, квадрата двучлена и суммы (разности) кубов. Умение применять формулы сокращенного умножения для преобразования алгебраических выражений. Умение выполнять деление многочлена на одночлен, если такое деление корректно. УУД Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы, проводить обоснованный вывод формул. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Разложение многочленов на множители Понятие о разложении многочлена на множители и его необходимости. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения и комбинации различных приемов. Сокращение алгебраических дробей. Тождества. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника по заданной теме. Выделение существенного, главного. Чтение и запись на математическом языке при выполнении разложения на множители. Комментирование решений, разобранных в учебнике. Работа в паре. Выполнение преобразования в виде разложения многочлена на множители по алгоритму и образцу. Решение уравнений, построение графиков уравнений, выполнение арифметических действий, связанных с разложением на множители, сокращение дробей. Пошаговый самоконтроль за выполнением указанных действий. Поиск и устранение ошибок. Подведение итогов. Самооценка знаний. | Умение видеть способ, которым данный многочлен можно разложить на множители и выполнять это разложение. Умение применять формулы сокращенного умножения для разложения многочлена на множители. Умение применять разложение многочлена на множители для решения уравнений, сокращения алгебраических дробей, доказательства делимости значения числового выражения на число, а также как способ рациональных вычислений. Понимание, что такое тождество и тождественное преобразование выражений. УУД Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы, проводить обоснованный вывод формул. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре. |
Функция 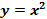 Функция
Функция 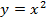 и ее график. Графическое решение уравнений. Функциональная символика. и ее график. Графическое решение уравнений. Функциональная символика.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль.
Чтение учебника и извлечение информации по заданной теме.
Изучение новых функций 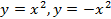 , графических моделей этих функций, свойств.
Построение и чтение графиков, в том числе кусочных функций. Проведение простейших исследований.
Участие в проектной деятельности «Описание реальных ситуаций с помощью кусочных функций».
Применение графических моделей для решения уравнений, неравенств, систем неравенств. Проверка найденных корней.
Исследование взаимного расположения графика кусочной функции и прямой y = a на предмет числа общих точек при различных значениях а.
Подведение итогов. Самооценка знаний. , графических моделей этих функций, свойств.
Построение и чтение графиков, в том числе кусочных функций. Проведение простейших исследований.
Участие в проектной деятельности «Описание реальных ситуаций с помощью кусочных функций».
Применение графических моделей для решения уравнений, неравенств, систем неравенств. Проверка найденных корней.
Исследование взаимного расположения графика кусочной функции и прямой y = a на предмет числа общих точек при различных значениях а.
Подведение итогов. Самооценка знаний.
| Понятие о функциях 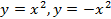 , умение вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Умение графически решать уравнения, системы уравнений и простейшие неравенства. Первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Умение строить речевые конструкции с использованием функциональной терминологии.
УУД
Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы. Умение проводить графическое исследование, читать графики. Умение осуществлять мини проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. , умение вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Умение графически решать уравнения, системы уравнений и простейшие неравенства. Первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Умение строить речевые конструкции с использованием функциональной терминологии.
УУД
Умение ставить учебные цели и задачи, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку, преодолевать трудности, корректировать свои знания.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение работать по аналогии, образцу, алгоритму, формуле. Умение сравнивать, обобщать, делать выводы. Умение проводить графическое исследование, читать графики. Умение осуществлять мини проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе.
|
| Элементы описательной статистики Данные и ряды данных. Упорядоченные ряды данных, таблицы распределения. Частота результата, таблица распределения частот, процентные частоты. Группировка данных. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Сбор, анализ, обобщение и представление статистической информации в виде таблиц и диаграмм. Мини проект. | Умение извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, организовывать информацию в виде таблиц и диаграмм, приводить примеры числовых данных, находить среднее значение, объем, моду, размах. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение собирать, анализировать, обобщать и представлять информацию в виде таблиц и диаграмм. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение | Постановка цели и задач на при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Самоконтроль. |
Содержание курса «Алгебра-8»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Повторение курса алгебры 7 класса | Актуализация знаний за курс алгебры 7 класса | |
| Алгебраические дроби Основные понятия об алгебраических дробях. Основное свойство алгебраической дроби. Сложение и вычитание, умножение и деление алгебраических дробей, возведение алгебраической дроби в степень. Преобразование рациональных выражений. Первые представления о простейших рациональных уравнениях. Степень с отрицательным целым показателем. | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и коррекция знаний. Чтение учебника с целью освоения новых знаний, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму при нахождении допустимых значений алгебраической дроби, сокращении алгебраических дробей, приведении к наименьшему общему знаменателю, сложении, вычитании, умножении и делении дробей, возведении дроби в степен, преобразовании выражений, содержащих степень с отрицательным показателем, решении рациональных уравнений. Поиск и отбор корней рационального уравнения. Моделирование реальных ситуаций с помощью рациональных уравнений. Работа в паре и группе. Подведение итогов. Самооценка знаний. | Представление о допустимых значениях алгебраической дроби и умение их находить. Знание основного свойства алгебраической дроби и умение применять его для преобразования дробей; умение выполнять действия с алгебраическими дробями, доказывать тождества. Понятие степени с целым показателем, умение вычислять значения степеней с отрицательным показателем, иллюстрировать примерами свойства степени с целым показателем. Первичные представления о рациональных уравнениях, методах их решения, отборе корней. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение работать по правилу, алгоритму, по аналогии. Умение анализировать свои действия, прогнозировать и оценивать результат. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
Функция 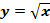 . Свойства квадратного корня
Рациональные, иррациональные числа, множество действительных чисел, стандартный вид числа. Квадратный корень из неотрицательного числа. Функция . Свойства квадратного корня
Рациональные, иррациональные числа, множество действительных чисел, стандартный вид числа. Квадратный корень из неотрицательного числа. Функция 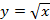 . Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. . Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни.
| Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль.
Самостоятельное изучение материала учебника, извлечение учебной информации о множестве рациональных и иррациональных чисел как части множества действительных чисел, осмысление ее и применение в учебной деятельности. Изображение чисел на числовойпрямой, сравнение, выполнение арифметических и алгебраических действий на множестве действительных чисел. Запись рациональных чисел в виде обыкновенной и десятичной периодической дроби. Прикидка возможности представления обыкновенной дроби в виде конечной десятичной дроби. Работа по правилу и по образцу. Составление алгоритма.
Знакомство с методом доказательства от противного.
Изучение свойств функций 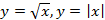 , построение их графиков. Построение и чтение графиков кусочных функций. Применение графических методов при решении уравнений, неравенств и систем уравнений. Исследование взаимного расположения графиков рассматриваемых функций и прямой , построение их графиков. Построение и чтение графиков кусочных функций. Применение графических методов при решении уравнений, неравенств и систем уравнений. Исследование взаимного расположения графиков рассматриваемых функций и прямой 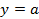 .
Проведение преобразований выражений, содержащих квадратный корень.
Работа в паре.
Поиск, обнаружение и устранение ошибок при выполнении вычислений,построении графиков и преобразовании выражений.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний. .
Проведение преобразований выражений, содержащих квадратный корень.
Работа в паре.
Поиск, обнаружение и устранение ошибок при выполнении вычислений,построении графиков и преобразовании выражений.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний.
| Систематизация знания о рациональных числах, понятия иррационального числа, множества действительных чисел. Умение находить приближения рациональных и иррациональных чисел, сравнивать и упорядочивать действительные числа. Освоение понятие квадратного корня из неотрицательного числа, умение строить график функции 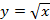 , описывать ее свойства, использовать график для нахождения квадратных корней и оценки их приближенных значений, вычислять квадратные корни с помощью калькулятора. Умение исследовать и доказывать свойства квадратных корней, применять их для преобразования выражений.Освоение понятие модуля действительного числа, функции , описывать ее свойства, использовать график для нахождения квадратных корней и оценки их приближенных значений, вычислять квадратные корни с помощью калькулятора. Умение исследовать и доказывать свойства квадратных корней, применять их для преобразования выражений.Освоение понятие модуля действительного числа, функции 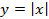 , умение строить ее график и описывать свойства, умение строить графики кусочных функций, описывать их свойства на основе графических представлений, использовать функциональную символику, строить речевые конструкции с использованием функциональной терминологии.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы.Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение работать по правилу, алгоритму, образцу. Умение осуществлять прикидку и оценку результата действий, примерно определять положение точки на числовой прямой. Умение логически мыслить, рассуждать, доказывать утверждения.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. , умение строить ее график и описывать свойства, умение строить графики кусочных функций, описывать их свойства на основе графических представлений, использовать функциональную символику, строить речевые конструкции с использованием функциональной терминологии.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы.Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение работать по правилу, алгоритму, образцу. Умение осуществлять прикидку и оценку результата действий, примерно определять положение точки на числовой прямой. Умение логически мыслить, рассуждать, доказывать утверждения.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации.
|
Квадратичная функция. Функция 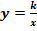 Функции
Функции 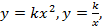 их свойства и графики. Параллельный перенос графика функции. Функция их свойства и графики. Параллельный перенос графика функции. Функция 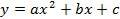 , ее свойства и график. Графическое решение квадратных уравнений. , ее свойства и график. Графическое решение квадратных уравнений.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка знаний.
Изучение графических моделей и свойств функций 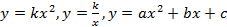 . Исследование зависимости графиков функций от значений коэффициентов. Проведение аналогии между аналитическим заданием квадратичной функции в виде . Исследование зависимости графиков функций от значений коэффициентов. Проведение аналогии между аналитическим заданием квадратичной функции в виде 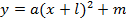 и и 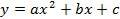 .
Наблюдение и исследование взаимного расположения графика функции .
Наблюдение и исследование взаимного расположения графика функции 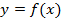 и графиков функций и графиков функций 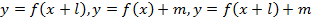 , обобщение результатов наблюдения в виде правила.
Составление алгоритмов построение параболы, гиперболы, построения графика функции с учетом параллельного переноса, решения квадратного уравнения графическим методом.
Участие в мини проектной деятельности «Гипербола и парабола как математические модели реальных ситуаций».
Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения квадратного уравнения (точки пересечения неточны или слишком удалены).
Работа в паре и группе.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний. , обобщение результатов наблюдения в виде правила.
Составление алгоритмов построение параболы, гиперболы, построения графика функции с учетом параллельного переноса, решения квадратного уравнения графическим методом.
Участие в мини проектной деятельности «Гипербола и парабола как математические модели реальных ситуаций».
Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения квадратного уравнения (точки пересечения неточны или слишком удалены).
Работа в паре и группе.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний.
| Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции 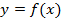 на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации. на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации.
|
| Квадратные уравнения Квадратные уравнения. Формулы корней квадратных уравнений. Рациональные уравнения. Рациональные уравнения как математические модели реальных ситуаций. Теорема Виета. Разложение квадратного трехчлена на линейные множители. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Изучение материала учебника с целью освоения понятия квадратного уравнения, его коэффициентов, понятия дискриминанта. Исследование квадратных уравнений на предмет числа корней. Вывод формулы для вычисления корней квадратного уравнения. Применение формул для решения квадратных уравнений. Составление алгоритма решения квадратного уравнения. Исследование соотношения между корнями квадратного уравнения и его коэффициентами, изучение теоремы Виета (прямой и обратной). Применение теоремы Виета для составления квадратных уравнений, подбора корней приведенного квадратного уравнения, разложения квадратного трехчлена на множители. Освоение методов решения алгебраических уравнений, сводящихся к квадратным. Моделирование реальных ситуаций с помощью квадратных и рациональных уравнений. Участие в мини проектной деятельности «Квадратные уравнения как математические модели реальных ситуаций». Осуществление самоконтроля решения, поиск и устранение ошибок. | Освоение понятия квадратного уравнения,умение распознавать квадратные уравнения, проводить исследование на предмет количества корней квадратного уравнения по дискриминанту и коэффициентам, умение применять формулы корней для решения квадратных уравнений. Умение решать рациональные уравнения и уравнения, сводящиеся к квадратным, умение решать текстовые задачи алгебраическим методом: составлять математическую модель – квадратное либо рациональное уравнение, решать его и интерпретировать результат. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить анализ, исследование, делать выводы. Умение проводить доказательство утверждений. Умениевыполнять действия по формуле, правилу, образцу. Умение моделировать с помощью уравнений реальные ситуации. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Неравенства Свойства числовых неравенств. Исследование функций на монотонность. Линейные и квадратные неравенства. Приближенные значения действительных чисел. Стандартный вид числа. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Самостоятельное чтение учебника с целью поиска информации и изучения материала на заданную тему. Иллюстрация свойств числовых неравенств на координатной прямой. Исследование функций на монотонность с помощью свойств числовых неравенств. Применение правил при решении неравенств. Исследование взаимосвязи решений квадратного неравенства и расположения параболы относительно прямойОх. Установление взаимосвязи между коэффициентома квадратного неравенства, знаком неравенства и наличием решений при отрицательном дискриминанте. Исследование квадратного уравнения с параметром на число корней. Поиск, обнаружение и устранение ошибок в решении линейных и квадратных неравенств. Участие в проектной деятельности «Моделирование реальных ситуаций с помощью квадратных неравенств» и «Где используются числа, записанные в стандартном виде?». Оценка и прикидка результата в приближенных вычислениях. | Знание свойств числовых неравенств, умение иллюстрировать их на координатной прямой, применять при исследовании функции на монотонность, доказательстве и решении неравенств. Умение распознавать линейные и квадратные неравенства, решать их, показывать решение неравенства в виде числового промежутка на числовой прямой. Умение находить приближенные значение числа с недостатком и с избытком, умение прикидывать и примерно оценивать результат. Умение представлять числа в стандартном виде и выполнять арифметические действия с числами, записанными в стандартном виде, использовать запись числа в стандартном виде для выражения размеров объектов, длительности процессов в реальном мире, сравнивать числа, записанные в стандартном виде. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить наблюдение, сравнение, анализ, исследование, обобщение. Умение работать по правилу и образцу.Умение выполнять прикидку, оценку размера объектов, длительности реальных процессов. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Элементы комбинаторики, статистики и теории вероятностей Простейшие комбинаторные задачи. Организованный перебор вариантов, дерево вариантов. Комбинаторное правило умножения. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Наблюдение, установление закономерности при переборе вариантов, построении дерева вариантов, вывод правила комбинаторного умножения. Мини проект «Комбинаторика вокруг нас». | Ознакомление с основными методами решения простейших комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение проводить организованный перебор вариантов, работать по правилу и образцу. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение | Постановка цели и задач при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Самоконтроль. |
Содержание курса «Алгебра-9»
| Содержание курса | Характеристика видов деятельности | Планируемые результаты обучения |
| Повторение курса алгебры 8 класса | Актуализация знаний за курс алгебры 8 класса | |
| Неравенства и системы неравенств Линейные и квадратные неравенства. Рациональные неравенства. Метод интервалов. Множества и операции над ними. Системы неравенств. | Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и коррекция знаний. Чтение учебника с целью освоения новых знаний, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму при решении неравенств и систем неравенств. Исследование знаков неравенства на числовых промежутках, отбор результатов решения. Поиск, обнаружение и исправление ошибок. Подведение итогов. Самооценка знаний. | Умение распознавать виды неравенств: линейное, квадратное, рациональное, и выбирать способ решения. Освоение различных методов решения неравенств и систем неравенств. Умение строить геометрическую модель решения неравенства и систем неравенств. Умение интерпретировать результат. Освоение понятий множество, элемент множества, пустое множество, подмножество, объединение и пересечение множеств. Умение показывать объединение и пересечение множеств с помощью кругов Эйлера, на числовой прямой и координатной плоскости. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение находить информацию в учебнике по заданной теме. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение работать по правилу, алгоритму, по аналогии. Умение анализировать свои действия, прогнозировать и оценивать результат. Умение взаимодействовать с товарищами по классу, работать в паре и группе. |
Системы уравнений
Рациональное уравнение с двумя переменными. Решение уравнения 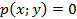 . Формула расстояния между двумя точками координатной плоскости. Уравнение окружности. Системы уравнений с двумя переменными. Решение систем уравнений. Неравенства и системы неравенств с двумя переменными. Методы решения систем уравнений. Системы уравнений как математические модели реальных ситуаций. . Формула расстояния между двумя точками координатной плоскости. Уравнение окружности. Системы уравнений с двумя переменными. Решение систем уравнений. Неравенства и системы неравенств с двумя переменными. Методы решения систем уравнений. Системы уравнений как математические модели реальных ситуаций.
| Постановка цели и задач. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное изучение материала учебника, извлечение учебной информации о методах решения систем уравнений. Интеграция знаний по алгебре и геометрии при изучении и применении в решении задач тем расстояние между двумя точками в координатной плоскости, уравнение окружности и уравнение прямой. Применение графических методов при решении уравнений, неравенств и систем уравнений. Исследование взаимного расположения графиков уравнений прямой, параболы, гиперболы и др. с окружностью. Моделирование реальных ситуаций в виде систем уравнений. Освоение нового вида задач на производительность. Участие в проектной деятельности «Системы уравнений как математические модели реальных ситуаций», «Жизнь вокруг нас: задачи на производительность». Работа в паре, группе. Поиск, обнаружение и устранение ошибок при выполнении вычислений, построении графиков и преобразовании выражений, решении уравнений, входящих в систему. Оценка достоверности и интерпретация результата решения. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. | Знание уравнений окружности, прямой, параболы, гиперболы, уравнений с модулем. Умение применять в решении систем уравнений графические и аналитические методы. Умение выполнять преобразование уравнений, входящих в систему, вводить новую переменную, интерпретировать и оценивать результат. Умение применять системы уравнений в решении задач. Освоение приемов решения задач на производительность труда. Умение проводить анализ и графическое исследование решения систем уравнений, в том числе с уравнением окружности, делать выводы и интерпретировать результат исследования. УУД Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий уровень восприятия. Умение работать по правилу, алгоритму, образцу. Умение осуществлять прикидку и оценку результата с точки зрения его достоверности. Умение логически мыслить, рассуждать, доказывать утверждения. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации. |
Числовые функции
Функция. Независимая и зависимая переменные. Определение числовой функции. Область определения и область значений функции. Естественная область определения функции. Способы задания функции. Свойства функций. Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функций. Функции 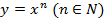 , их свойства и графики. Функции , их свойства и графики. Функции 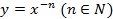 , их свойства и графики. Функция , их свойства и графики. Функция 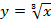 , ее свойства и график. , ее свойства и график.
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка знаний.
Описание свойств функций 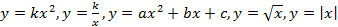 . Исследование функций.
Задание функций разными способами и построение графиков.
Изучение новых свойств функций: четность и нечетность. Исследование функций на четность и нечетность согласно алгоритму.
Изучение свойств функций . Исследование функций.
Задание функций разными способами и построение графиков.
Изучение новых свойств функций: четность и нечетность. Исследование функций на четность и нечетность согласно алгоритму.
Изучение свойств функций 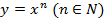 , , 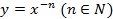 , , 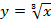 , построение их графиков. Применение графиков функций к решению уравнений, неравенств, систем уравнений и неравенств.
Участие в проектной деятельности «Описание реальных процессов с помощью графиков функций , построение их графиков. Применение графиков функций к решению уравнений, неравенств, систем уравнений и неравенств.
Участие в проектной деятельности «Описание реальных процессов с помощью графиков функций 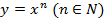 , , 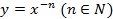 ».
Поиск решения в проблемной ситуации: неточность и недостаточность применения графического метода решения уравнения ».
Поиск решения в проблемной ситуации: неточность и недостаточность применения графического метода решения уравнения 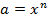 , – по аналогии с решением проблемы , – по аналогии с решением проблемы 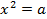 . Знакомство с новой математической моделью . Знакомство с новой математической моделью 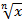 .
Работа в паре и группе.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний. .
Работа в паре и группе.
Подведение итогов: что нового узнали, чему научились. Самооценка знаний.
| Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, способы их задания, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции 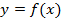 на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств. Умение находить решение в проблемной ситуации.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий и далее на формальный уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации. на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств. Умение находить решение в проблемной ситуации.
УУД
Умение ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку.
Умение осознанно читать математический текст, находить информацию в учебнике по заданной теме. Умение на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ, делать выводы. Умение переводить информацию с наглядно-интуитивного уровня на рабочий и далее на формальный уровень восприятия. Умение решать по образцу и алгоритму, проводить аналогии. Умение осуществлять проектную деятельность.
Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение быстро включаться в деятельность, взаимодействовать с товарищами по классу в деловой ситуации.
|
| Прогрессии Числовые последовательности. Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей. Арифметическая прогрессия. Формула n-го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. . Формула n-го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты. | Постановка цели и задач на уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Изучение материала учебника с целью освоения понятиями:последовательность, задание последовательности, график последовательности, формула n-го члена. Освоение понятий арифметическая и геометрическая прогрессии, вывод формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Исследование последовательностей, в том числе арифметической и геометрической прогрессий. Выполнение упражнений на применение формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Моделирование банковских расчетов с помощью прогрессий. Работа в группе. Участие в проекте «Прогрессии как математические модели реальных ситуаций». Осуществление самоконтроля решения, обнаружение, поиск и устранение ошибок. | Ознакомление с новой математической моделью – числовая последовательность, арифметическая и геометрическая прогрессии, способами задания последовательностей, формуламиn-го члена, графикамичисловых последовательностей. Знание формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Освоение новой терминологии, новых символов и обозначений. Умение распознавать арифметическую и геометрическую прогрессии, находить неизвестный компонент формулы n-го члена, формулы суммы конечной арифметической или геометрической прогрессии, применять характеристическое свойство прогрессии. Знание формулы сложных процентов. Умение производить несложные расчеты процентов банковских операций. Умение моделировать реальные ситуации с помощью последовательностей. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение читать утверждения, записанные на математическом языке в знаково-символьной форме. Умение наблюдать, находить закономерности, выдвигать гипотезы, проводить обоснование. Умение переходить от наглядно-интуитивного уровня восприятия к рабочему и далее формальному уровню. Умение проводить анализ, исследование, делать обоснованные выводы. Умение выполнять действия по формуле, правилу, образцу. Умение моделировать реальные ситуации. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе. |
| Элементы комбинаторики, статистики и теории вероятностей Комбинаторные задачи. Правило умножения. Факториал. Перестановки. Статистика – дизайн информации. Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения. Вероятность. Событие. Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Экспериментальные данные и вероятности событий. Статистическая устойчивость и статистическая вероятность. | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль и самооценка достижений. Наблюдение, установление закономерности при переборе вариантов, построении дерева вариантов, вывод правила комбинаторного умножения. Участие в проведении эксперимента. Сбор, обработка и представление информации. Ознакомление с новой математической моделью – классической вероятностной схемой и применение формулы для подсчета вероятности. Математическое моделирование простейших вероятностных ситуаций. Мини проект «Игры и вероятности событий». | Умение применять основные методы решения комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций. Освоение понятия факториал, умение применять определение факториала в решении комбинаторных задач. Ознакомление с новой математической моделью – классической вероятностной схемой и формулой для подсчета вероятности. Знание основных видов случайных событий: достоверные, невозможные, несовместные события, события, противоположные данным; сумма двух случайных событий. Умение проводить доказательство формул и теорем. Знание числовых характеристик информации, полученной в результате эксперимента. Умение проводить эксперимент. Умение использовать методы статистической обработки результатов измерений, полученных при проведении эксперимента. Умение группировать данные, проводить обработку данных, представлять информацию в виде таблиц, диаграмм, гистограмм, графиков. УУД Умение ставить цель и задачи, планировать деятельность, проводить самоанализ и самоконтроль деятельности. Умение проводить эксперимент, добывать, обрабатывать и представлять информацию, работать по правилу и образцу. Умение контактировать со всеми участниками учебного процесса. |
| Итоговое повторение Числовые выражения. Алгебраические выражения. Функции и графики. Уравнения и системы уравнений. Неравенства и системы неравенств. Задачи на составление уравнений или систем уравнений. Арифметическая и геометрическая прогрессии. | Постановка цели и задач при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Подготовка к итоговой аттестации по математике. Самоконтроль. |
ОПИСАНИЕ УЧЕБНО-МЕТОДИЧЕСКОГО И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОГО ОБЕСПЕЧИВАНИЯ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА:
1).Методические пособия для учителя:
· А.Г.Мордкович Алгебра 7-9-х классов: метод. Пособие для учителя-М: Мнемозина, 2010
· Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание второе, переработанное. Под редакцией Ф.Ф. Лысенко. Ростов-на-Дону: Легион, 2007.
· Задачи повышенной трудности в курсе алгебры 7-9 классов: Книга для учителя. Н.П. Кострикина. – М.: Просвещение, 1991.
· История математики в школе. VII-VIIIкл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982.
· Поурочные разработки по алгебре к учебнику А.Г.Мордковича, П.В. Семенова «Алгебра7 класс»/ Издательство «Учитель»
2).Дополнительная литература
· Агаханов Н.Х. Математика. Всероссийские олимпиады. 5-11 классы./Агаханов Н.Х..-М.:Просвещение, 2010
· Фарков А.В. Математические олимпиады в школе. 5-11 классы/ А.В. Фарков. – М.: Айрис-Пресс, 2010
3). Интернет-ресурсы, рекомендуемых для использования в работе учителями математики.
1. http://school-collection.edu.ru − хранилище единой коллекции цифровых образовательных ресурсов, где представлен широкий выбор электронных пособий;
2. http://wmolow.edu.ru − федеральная система информационно-образовательных ресурсов (информационный портал);
3. http://fcior.edu.ru - хранилище интерактивных электронных образовательных ресурсов;
4. www/ziimag.narod.ru – сайт автора А. Г. Мордковича «Практика развивающего обучения»
5. http://www.numbernut.com/ − все о математике. Материалы для изучения и преподавания математики в школе. Тематический сборник: числа, дроби, сложение, вычитание и пр. Теоретический материал, задачи, игры, тесты;
6. http://www.math.ru − удивительный мир математики/ Коллекция книг, видео-лекций, подборка занимательных математических фактов. Информация об олимпиадах, научных школах по математике. Медиатека;
7. http://physmatica.narod.ru − «Физматика». Образовательный сайт по физике и математике для школьников, их родителей и педагогов;
8. http:www.int.ru – сеть творческих учителей. Методические пособия для учителя; учебно-методические пособия; словари; справочники; монографии; учебники; рабочие тетради; статьи периодической печати;
9. http://methath.chat.ru – Методика преподавания математики Материалы по методике преподавания математики; обсуждение наболевших вопросов преподавания математики в средней школе. Авторы — учителя математики, имеющие большой опыт преподавательской и методической работы
10. http://www.bymath.net – Средняя математическая интернет-школа: страна математики. Учебные пособия по разделам математики: теория, примеры, решения. Задачи и варианты контрольных работ;
11. http://www.mccme.ru – Московский центр непрерывного математического образования. Документы и статьи о математическом образовании. Информация об олимпиадах, дистанционная консультация;
12. http://teacher.ru – «Учитель.ру». Педагогические мастерские, Интернет-образование. Дистанционное образование. Каталог ресурсов «в помощь учителю»;
13. Министерство образования РФ. – Режим доступа : http://www.informika.ru; http://www.ed.gov.ru; http://www.edu.ru
14. Тестирование online: 5–11 классы. – Режим доступа : http://www.kokch.kts.ru/cdo
15. Педагогическая мастерская, уроки в Интернет и многое другое. – Режим доступа : http:// teacher.fio.ru
16. Новые технологии в образовании. – Режим доступа : http://edu.secna.ru/main
17. Путеводитель «В мире науки» для школьников. – Режим доступа : http://www.uic.ssu. samara.ru/~nauka
18. Мегаэнциклопедия Кирилла и Мефодия. – Режим доступа : http://mega.km.ru
19. Сайты энциклопедий, например: http://www.rubricon.ru; http. – Режим доступа ://www. encyclopedia.ru
20. Единая коллекция цифровых образовательных ресурсов по математике. – Режим доступа : http://school-collection.edu.ru/collection
4).Информационно-коммуникативные средства:
Коллекция мультимедийных уроков Кирилла и Мефодия «Алгебра 7, 8, 9 класс»
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО АЛГЕБРЕ 7 КЛАСС
| № п/п | Наименование темы | Всего часов | Из них |
| Контрольных работ/проверочных работ | |||
| Повторение курса 6 класса | 4 | ||
| 1. | Математический язык. Математическая модель. | 12 | Входная К/р№1 |
| 2. | Линейная функция. | 12 | К/р№2 |
| 3. | Системы двух линейных уравнений с двумя переменными. | 11 | К/р№3 |
| 4. | Степень с натуральным показателем и ее свойства. | 8 | Проверочная работа |
| 5. | Одночлены. Операции над одночленами. | 9 | К/р№4 |
| 6. | Многочлены. Операции над многочленами. | 18 | К/р№5 |
| 7. | Разложение многочленов на множители. | 18 | К/р№6 |
| 8. | Функция у=х². | 7 | Проверочная работа |
| 9. | Элементы описательной статистики. Повторение. | 6 | К/р№7 |
| Всего | 105 | 7 | |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО АЛГЕБРЕ 8 КЛАСС
| № п/п | Наименование темы | Всего часов | Из них |
| Контрольных работ/проверочных работ | |||
| Повторение курса 7 класса | 5 | Входная | |
| 1. | Алгебраические дроби. | 21 | Проверочная работа, К/р№1 |
| 2. | Функция у= 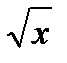 . Свойства квадратного корня. . Свойства квадратного корня.
| 18 | К/р№2 |
| 3. | Квадратичная функция. Функция у= 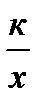 . .
| 18 | К/р№3 Проверочная работа |
| 4. | Квадратные уравнения. | 21 | К/р№4, К/р №5 |
| 5. | Неравенства. | 15 | К/р№6 |
| 6. | Элементы комбинаторики. Обобщающее повторение курса алгебры за 8 класс. | 7 | Итоговая контрольная работа№7 |
| Всего | 105 | 7 | |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО АЛГЕБРЕ 9 КЛАСС
| № п/п | Наименование темы | Всего часов | Из них |
| Контрольных работ/проверочных работ | |||
| Повторение 8 класса. | 4 | Входная | |
| 1. | Неравенства. Системы неравенств. | 16 | К/р№1 |
| 2. | Системы уравнений | 14 | К/р№2 |
| 3. | Числовые функции. | 24 | К/р№3, К/р№4 |
| 4. | Прогрессии. | 19 | К/р №5 |
| 5. | Элементы комбинаторики, статистики и теории вероятностей. | 10 | К/р№6 |
| 6. | Обобщающее повторение курса алгебры за 9 класс. | 15 | Итоговая контрольная работа№7 |
| Всего | 102 | 7 | |
Умение
-изобразить на координатной плоскости точки, координаты которых удовлетворяют неравенству, аргументированно отвечать на поставленные вопросы, участвовать
в диалоге;
-решить задачу, выделяя три этапа математического моделирования, объяснить изученные положения на самостоятельно подобранных конкретных примерах по теме, правильно оформлять работу, отражать в письменной форме свои решения, выступать с решением проблемы.
Виртуальная школа Кирилла и Мефодия
Решение квадратных неравенств.
3
Иметь представление о квадратном неравенстве, о знаке объединения множеств, алгоритме решения квадратного неравенства, о методе интервалов; о решении квадратичных неравенств с параметром.
Знание алгоритма решения квадратного неравенства по алгоритму и методом интервалов.
Умение
-свободно решать квадратные неравенства методом интервалов;
- решать квадратные неравенства, применяя равносильные преобразования выражений, решать квадратичные неравенства с параметром, объяснять изученные положения на самостоятельно подобранных конкретных примерах.
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1 ИМЕНИ АЛЕКСАНДРА КИРИЛЛОВИЧА ПРОСОЕДОВА
«Согласовано» «Утверждаю»
Зам.директора по УВР: Директор МОУ СОШ №1
_____________
__________________
«___»_________2015 г «____»__________2015г
Рабочая программа
По алгебре для 7-9 классов
(среднее общее образование)
Учитель математики: Шарикова Ирина Евгеньевна
Рассмотрено и обсуждено на заседании Тематическое планирование откорректировано
методического совета Протокол №_______от «_____» ________2016 г.
Протокол №_____ от «___»_________ 2015 г Зам. директора по УВР:
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа основного общего образования по алгебре составлена на основе авторской программы И.И.Зубаревой и А.Г.Мордковича, Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. Настоящая рабочая программа разработана применительно к учебной программе А.Г. Мордковича «Алгебра» для 7-9 -х классов и ориентирована на использование учебно-методического комплекта:
- А.Г. Мордкович Алгебра 7 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010-2013
- А.Г.Мордкович Алгебра 7 класс: метод. Пособие для учителя-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 7 класс: самостоятельные работы-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 7 класс: контрольные работы-М: Мнемозина, 2010-2013
- А.Г. Мордкович Алгебра 8 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010-2013
- А.Г.Мордкович Алгебра 8 класс: метод. Пособие для учителя-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 8 класс: самостоятельные работы-М: Мнемозина, 2010-2013
- Л.А.Александрова Алгебра 8 класс: контрольные работы-М: Мнемозина, 2010-2013
- А.Г. Мордкович Алгебра 9 класс: учебник для учащихся общеобразовательных учреждений и задачник- М: Мнемозина , 2010
- А.Г.Мордкович Алгебра 9 класс: метод. Пособие для учителя-М: Мнемозина, 2010
- Л.А.Александрова Алгебра 9 класс: самостоятельные работы-М: Мнемозина, 2010
- Л.А.Александрова Алгебра 9 класс: контрольные работы-М: Мнемозина, 2010
- А.Г.Мордкович Алгебра 7-9 кл.:тесты-М: Мнемозина 2010-2013
- Е.М.Ключникова Рабочая тетрадь по алгебре к учебнику А.Г.Мордковича «Алгебра. 7 класс», «Алгебра. 8 класс».
Представленная программа выполняет две основные функции:
· информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития обучающихся 7-9 классов средствами данного учебного предмета;
· организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации обучающихся.
Дата: 2019-02-25, просмотров: 364.