Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1

 

 

 

 

 

 

5.

Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.

 

2

 

Знать правило умножения дробей, выполнять соответствующие преобразования. Знать правило деления дробей, выполнять соответствующие преобразования. Знать правило возведения дроби в степень.

Знание: - правил умножения и деления алгебраических дробей, возведения дроби в степень; - алгоритма умножения и деления дробей, возведение дроби в степень. Умение упрощать выражения, применяя формулы сокращенного умножения, доказывать тождества, формулировать выводы, давать определения, приводить доказательства.

 

  С-6,7

 

6.

Преобразование рациональных выражений.

3

 

Уметь выполнять все действия с рациональными дробями.

Знание способов преобразования рациональных выражений с алгебраическими дробями. Умение выполнять преобразования рациональных выражений, используя все действия с алгебраическими дробями, решать рациональные уравнения, решать задачи, выделяя три этапа математического моделирования.

 

С-8

 

7.

Первые представления о рациональных уравнениях.

2

 

Учитывать при решении область допустимых значений уравнения.

Знание алгоритма решения рационального уравнения, составления математической модели реальных ситуаций. Умение: -решать рациональные уравнения, применяя формулы сокращенного умножения при их упрощении,; -составлять и решать задачи, выделяя три этапа математического моделирования.

 

С-9

 

8.

Степень с отрицательным целым показателем.

2

 

Уметь находить значение степеней с целым показателем.

 

 

С-10

 

К-1

Контрольная работа по теме «Преобразование рациональных выражений».

1

 

Знать свойства 1-5 и выполнять по ним преобразования одночленов.

Умение самостоятельно выбирать рациональный способ преобразования рациональных выражений, решения рациональных уравнений способом освобождения от знаменателей, составлять математическую модель реальных ситуаций.

 

 

 

Обобщающий урок по теме «Алгебраические дроби».

1

 

 

 

 

 

 

          Функция у= 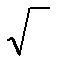х. Свойства квадратного корня. 18 часов

Цели ученика:

-иметь представление о квадратном корне, о подкоренном выражении, об иррациональных числах, о кубическом корне из неотрицательного числа, о корне n-ной степени из неотрицательного числа;

-иметь представление о преобразовании выражений, содержащих операцию извлечения квадратного корня, об освобождении от иррациональности в знаменателе;

-овладеть умениями:

-извлекать квадратный корень и корень с n-ной степени из неотрицательного числа; оценивать неизвлекаемые корни, находить их приближенное значение; решения уравнений, содержащих радикал;

-использовать алгоритм извлечения квадратного корня.

Цели педагога:

-формирование умений извлечения квадратного корня и корня n-ной степени из неотрицательного числа;

-помощь в овладении умением построения графика функции у= 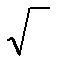х и описания ее свойств;

-помощь в овладении навыками использовать алгоритм извлечения квадратного корня; решения уравнений, содержащих радикал.

9.

Рациональные числа.

2

 

Уметь представлять числа в виде а= 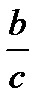, знать определение рационального числа. Уметь выполнять действия с рациональными числами.

 

 

 

С-11

 

10.

Понятие квадратного корня из неотрицательного числа.

2

 

Знать определение квадратного корня, уметь читать и записывать их, выполнять вычисления вида .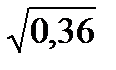

Знание способа извлечения квадратного корня из неотрицательного числа, действительных и иррациональных чисел.

Умение решать простейшие уравнения.

 

С-12

Виртуальная школа Кирилла и Мефодия

11.

Иррациональные числа.

1

 

Рассмотреть примеры иррациональных чисел.

Иметь представление об иррациональном числе.

Умение объяснить изученные положения на самостоятельно подобранных конкретных примерах, доказать иррациональность числа, определять понятия, приводить доказательства.

 

С-13

Виртуальная школа Кирилла и Мефодия

12.

Множество действительных чисел.

1

 

 

Знание о делимости целых чисел;
о делении с остатком.

Умение решать задачи с целочисленными неизвестными, объяснять изученные положения на самостоятельно подобранных конкретных примерах, воспроизводить изученные правила и понятия, подбирать аргументы, соответствующие решению.

 

С-14

 

13.

Функция у= 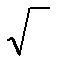х, ее свойства и график.

2

 

Уметь определять область определения и область значений функции у = ,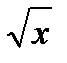

уметь строить график данной функции.

Знание алгоритма построения графика функции 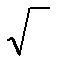х и ее свойств.

Умение читать графики функций, решать графически уравнения и системы уравнений, излагать информацию, обосновывая свой подход, воспроизводить изученные правила и понятия.

 

С-15

Виртуальная школа Кирилла и Мефодия

14.

Свойства квадратных корней.

2

 

Знать формулы

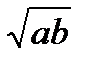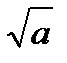
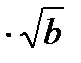= , где а≥0, в≥0;  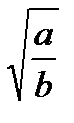= 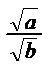где а≥0, в≥0 и уметь выполнять преобразования по этим формулам с числами.

 

Знание свойств квадратных корней.

Умение применять свойства корней при нахождении значения выражений, выполнять более сложные упрощения выражений наиболее рациональным способом, определять понятия, приводить доказательства.

 

С-16

Виртуальная школа Кирилла и Мефодия

15.

Преобразование выражений, содержащих операцию извлечения квадратного корня.

4

 

Уметь приводить подобные слагаемые, раскрывать скобки, использовать формулы сокращенного умножения в примерах с квадратными корнями.

Умение:

- оценивать неизвлекаемые корни, находить их приближенные значения;

-преобразовывать выражения, используя операцию извлечения квадратного корня, освобождения от иррациональности в знаменателе.

 

С-17-20

Виртуальная школа Кирилла и Мефодия

К-2