Тождественные частицы – это частицы, имеющие одинаковую массу, заряд, спин.Возьмем систему из двух электронов и пронумеруем их. С классической точки зрения электрон движется по траектории, поэтому в каждый момент времени мы можем сказать, будет ли это электрон 1 или электрон 2. Поменяв местами и скоростями электроны, мы получим другое состояние, которое отличается от предыдущего только нумерацией. Т.о. тождественные частицы в классической механике принципиально различимы.

В квантовой механике состояние системы описывается волновой функцией. Она физического смысла не имеет, а физический смысл имеет 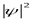. Микрочастица размазана в пространстве. В нашем случае, если обнаружить в какой-то момент времени один из электронов, то принципиально невозможно определить, будет ли это электрон 1 или 2. Если две одинаковые частицы поменять местами, то результат такого обмена невозможно обнаружить экспериментально. Т.е. при перестановке частиц состояние не меняется. Одинаковые частицы принципиально неразличимы, а о состоянии частиц можно говорить как о состоянии системы одинаковых частиц в целом. Это можно сформулировать в принцип неразличимости тождественных частиц: В системе одинаковых частиц реализуются только такие состояния, которые не меняются при перестановке местами любых двух частиц. Экспериментально тождественные частицы различить невозможно.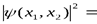 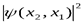,x – совокупность пространственных и спиновых координат. (Например, проекция спина электрона может принимать значение 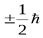- это и есть спиновая координата). Пусть состояние системы описывается волновой функцией 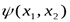. Переставим местами частицы. Эту операцию можно рассматривать как действие на функцию линейного оператора перестановки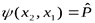 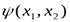. Переставим рассматриваемые частицы вторично, получим исходную функцию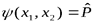 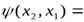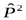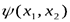. Отсюда 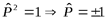, допустимы функции двух типов:

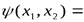
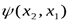- это симметричная функция – при перестановке частиц волновая функция не меняется,

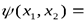
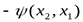- это антисимметричная функция – при перестановке частиц волновая функция изменяет знак на противоположный. Характер симметрии не зависит от времени. Частицы, состояния которых описываются симметричными волновыми функциями, называются бозонами или бозе-частицами. Эти частицы подчиняются статистике Бозе-Эйнштейна. Частицы, состояния которых описываются антисимметричными волновыми функциями, называются фермионами. Они подчиняются статистике Ферми-Дирака. Оказалось, что симметричные волновые функции описывают состояния микрочастиц с целым спином, а антисимметричные - состояния микрочастиц с полуцелым целым спином. Эту связь между спином и статистикой установил Паули исходя из общих принципов квантовой теории – релятивистской инвариантности, неотрицательности полной энергии, причинности т.д. К бозонам относятся фотоны, 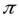- мезоны и др. К фермионам относятся электроны, протоны, нейтроны, нейтрино и т.д. Принадлежность сложной частицы (атома, молекулы) к бозонам или фермионам определяется ее спином: если сложная частица состоит из четного числа фермионов, то сложная частица – бозон, если из нечетного числа фермионов, то она – фермион.

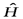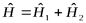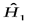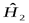Пусть система состоит из двух одинаковых невзаимодействующих частиц. - оператор Гамильтона всей системы, , где , -каждой из частиц, причем 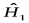действует только на 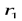- координаты первой частицы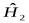, а - на 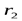- координаты второй частицы. Уравнение Шредингера 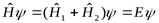. Можно показать, что решение уравнения Шредингера можно представить в ви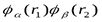де: , где 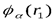- решение уравнения 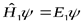, а 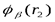- решение уравнения 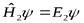, причем 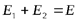. В силу тождественности частиц функция 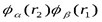также является решением уравнения Шредингера. Но ни одна из этих функций не удовлетворяет принципу симметрии или антисимметрии. Но из этих функций можно составить комбинации, являющиеся решениями уравнения Шредингера:

Симметрична функция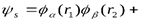

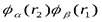
Антисимметричная функция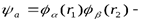

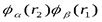
Фермионы описываются антисимметричными функциями. Исходя из последней формулы, можно сказать, что в системе одинаковых фермионов не может быть двух частиц, находящихся в одном и том же состоянии, поскольку тогда 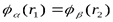и волновая функция будет равна нулю. Таким образом, принцип Паули: В системе тождественных фермионов не может быть двух частиц, находящихся в одном и том же состоянии. Первоначально Паули сформулировал свой принцип: в атоме не может быть двух электронов, характеризующихся одинаковой четверкой квантовых чисел. Принцип Паули сформулирован для невзаимодействующих частиц. Но он оказался плодотворным для обоснования периодической системы элементов.

Что касается бозонов, то на их состояния принцип симметрии волновых функций не накладывает ни каких ограничений. В одном и том же состоянии может находиться любое число одинаковых бозонов. Это следует из вида волновой функции.

Если тождественные частицы имеют оди­наковые квантовые числа, то их волновая функция симметрична относительно пере­становки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинако­вых состояниях, так как для фермионов волновая функция должна быть антисим­метричной. Обобщая опытные данные, В. Паули сформулировал принцип, соглас­но которому системы фермионов встреча­ются в природе только в состояниях, опи­сываемых антисимметричными волновыми функциями (квантово-механическая фор­мулировка принципа Паули).

Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения кванто­вой механики: в системе одинаковых фермионов любые два из них не могут одно­временно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Напомним, что состояние электрона

в атоме однозначно определяется набором

четырех квантовых чисел: главного n (n=1, 2, 3, ...), орбитального l (l=0, 1, 2, ..., n-1), магнитного m_l (m_l= -l, ..., -1, 0,

+ 1, ..., +l),

магнитного спинового m_s (m_s=+¹/₂,-¹/₂).

Распределение электронов в атоме подчиняется принципу Паули, который мо­жет быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с оди­наковым набором четырех квантовых чи­сел n, l, m_l и m_s, т. е.

Z (n, l, m_l, m_s)=0 или 1,

где Z (n, l, m_l, m_s) — число электронов, на­ходящихся в квантовом состоянии, описы­ваемом набором четырех квантовых чисел: n, l, m_l, m_s. Таким образом, принцип Пау­ли утверждает, что два электрона, связан­ные в одном и том же атоме, различаются значениями по крайней мере одного кван­тового числа.

Согласно формуле (223.8), данному n соответствует n² различных состояний, отличающихся значениями l и m_l. Кванто­вое число m_s может принимать лишь два значения (±¹/₂). Поэтому максимальное число электронов, находящихся в состоя­ниях, определяемых данным главным кван­товым числом, равно

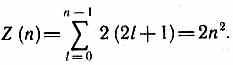
Совокупность электронов в многоэлек­тронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из обо­лочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n-1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и маг­нитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l+1). Обозна­чения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 6.